-基本初等函数的导数公式及四则运算
- 格式:ppt
- 大小:727.50 KB
- 文档页数:35

基本初等函数的导数公式及导数的运算法则(一)基本初等函数的导数公式表x y x y xy x y y x y cos )6(log )5(ln )4(1)3(5)2()1(125======、求下列函数的导数例 例处的切线方程。
在、求函数2cos 2π==x x y(二)导数的四则运算法则:(2)推论:[]''()()cf x cf x = (常数与函数的积的导数,等于常数乘函数的导数)例3、根据基本初等函数的导数公式和导数运算法则,求下列函数的导数.(1)323y x x =-+(2)y = (3)sin ln y x x x =⋅⋅;(4)4x x y =; (5)1ln 1ln x y x -=+. (6)2(251)x y x x e =-+⋅;三.课堂练习1、求下列函数的导数:)1()3( )sin ()2( cos )1(1)1(2322+=-=+-=x f y x b ax y xx x y ω 2、已知曲线C :y =3 x 4-2 x 3-9 x 2+4,求曲线C 上横坐标为1的点的切线方程;3、处的导数。
在求3332=++=x x x y 4、处的切线方程。
,在点求曲线)20(1P e y x += ______________________1216______________)42()04(4522处的切线方程为垂直,则过点的切线与直线上的点,若过点是曲线、的坐标为,则于处的切线恰好平行,若曲线上一点,、,上两点、曲线P x y P x y P P AB P B A x x y +-==-= 7、曲线3()2f x x x =+-在0P 点处的切线平行于直线41y x =-,则0P 点的坐标为 .8、已知抛物线2y x bx c =++上的点(1,2)处的切线与直线2y x =-平行,求b ,c 的值。





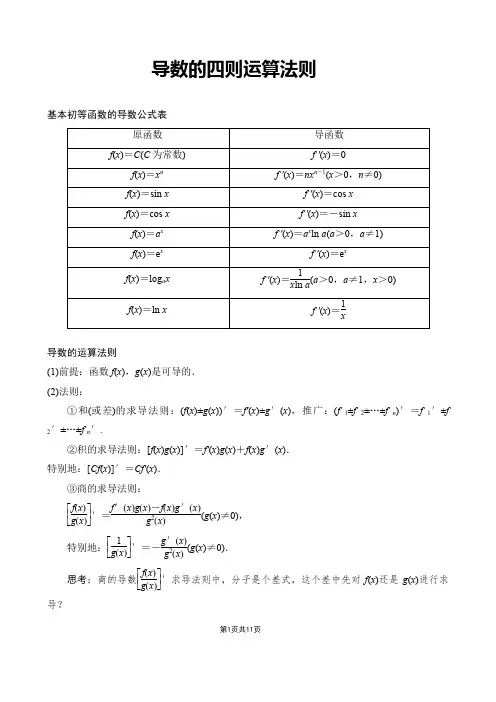
第1页共11页导数的四则运算法则基本初等函数的导数公式表导数的运算法则(1)前提:函数f (x ),g (x )是可导的. (2)法则:①和(或差)的求导法则:(f (x )±g (x ))′=f′(x )±g ′(x ),推广:(f 1±f 2±…±f n )′=f 1′±f2′±…±f n ′.②积的求导法则:[f (x )g (x )]′=f′(x )g (x )+f (x )g ′(x ). 特别地:[Cf (x )]′=Cf′(x ).③商的求导法则:⎣⎢⎡⎦⎥⎤f (x )g (x )′=f ′(x )g (x )-f (x )g ′(x )g 2(x )(g (x )≠0),特别地:⎣⎢⎡⎦⎥⎤1g (x )′=-g ′(x )g 2(x )(g (x )≠0).思考:商的导数⎣⎢⎡⎦⎥⎤f (x )g (x )′求导法则中,分子是个差式,这个差中先对f (x )还是g (x )进行求导?第2页共11页[提示] 先对f (x )求导,即f′(x )g (x ),再对g (x )求导,即f (x )g ′(x ).1.下列结论不正确的是( ) A .若y =3,则y ′=0 B .若f (x )=3x +1,则f′(1)=3 C .若y =-x +x ,则y ′=-12x+1D .若y =sin x +cos x ,则y ′=cos x +sin xD [D 项,∵y =sin x +cos x ,∴y ′=(sin x )′+(cos x )′=cos x -sin x .] 2.设y =-2e x sin x ,则y ′等于( ) A .-2e x cos x B .-2e x sin x C .2e x sin xD .-2e x (sin x +cos x )D [y ′=-2(e x sin x +e x cos x )=-2e x (sin x +cos x ).] 3.已知函数f (x )=ln xx ,则f′(1)=________. 1 [∵f′(x )=1x ×x -ln x x 2=1-ln xx 2,∴f′(1)=1.]用导数的求导法则求导数 【例1】 求下列函数的导数: (1)y =2x 2+1x -3x 3; (2)y =x +3x 2+3; (3)y =e x cos x +sin x ;(4)y =x 3+lg x .[思路探究] 观察函数的特征,可先对函数式进行合理变形,然后利用导数公式及相应的四则运算法则求解.[解] (1)∵y =2x 2+x -1-3·x -3, ∴y ′=4x -x -2-3·(-3)x -4=4x -1x 2+9x 4. (2)y ′=1·(x 2+3)-2x (x +3)(x 2+3)2=-x 2-6x +3(x 2+3)2.(3)y ′=(e x cos x +sin x )′=(e x cos x )′+(sin x )′第3页共11页=(e x )′cos x +e x (cos x )′+cos x =e x cos x -e x sin x +cos x . (4)y ′=3x 2+1x ln 10.应用基本初等函数的导数公式和求导的四则运算法则可迅速解决一些简单函数的求导问题,要透彻理解函数求导法则的结构特点,准确熟记公式,还要注意挖掘知识的内在联系及其规律.对比较复杂的求导问题,可先进行恒等变形,再利用公式求导.提醒:当不易直接应用导数公式时,应先对函数进行化简,再求导.求下列函数的导数: (1)y =1x 2+sin x 2cos x 2; (2)y =x ⎝ ⎛⎭⎪⎫x 2-32x -6+2;(3)y =cos x ln x ;(4)y =xe x .[解] (1)y ′=⎝ ⎛⎭⎪⎫1x 2+sin x 2cos x 2′=(x -2)′+()12sin x ′ =-2x -3+12cos x =-2x 3+12cos x . (2)y ′=⎝ ⎛⎭⎪⎫x 3-32x 2-6x +2′=(x 3)′-⎝ ⎛⎭⎪⎫32x 2′-(6x )′+(2)′=3x 2-3x -6. (3)y ′=(cos x ln x )′ =(cos x )′ln x +cos x (ln x )′ =-sin x ln x +cos xx .第4页共11页(4)y ′=⎝ ⎛⎭⎪⎫x e x ′=(x )′e x -x (e x)′(e x )2=e x -x e x e 2x =1-xe x . 导数运算法则的应用 [探究问题]1.导数的和、差运算法则求导能拓展到多个函数吗? [提示] [f 1(x )±f 2(x )±…±f n (x )]′=f 1′(x )±f 2′(x )±…±f′n (x ). 2.导数的积、商运算法则有哪些相似的地方?区别是什么?[提示] 对于积与商的导数运算法则,应避免出现“积的导数就是导数的积,商的导数就是导数的商”这类想当然的错误,应特别注意积与商中符号的异同,积的导数法则中是“+”,商的导数法则中分子上是“-”.【例2】 已知函数f (x )=ln x -ax +1-ax -1(a ∈R ).当a =-1时,求曲线y =f (x )在点(2,f (2))处的切线方程.[思路探究] 先求导,再求切线斜率,根据点斜式得切线方程. [解] 因为当a =-1时,f (x )=ln x +x +2x -1,x ∈(0,+∞). 所以f′(x )=x 2+x -2x 2,x ∈(0,+∞),因为f′(2)=1,即曲线y =f (x )在点(2,f (2))处的切线斜率为1.又f (2)=ln 2+2, 所以曲线y =f (x )在点(2,f (2))处的切线方程为y -(ln 2+2)=x -2, 即x -y +ln 2=0.1.(变换条件)本典例函数不变,条件变为“曲线y =f (x )在点(2,f (2))处的切线方程为x第5页共11页(1)此类问题往往涉及切点、切点处的导数、切线方程三个主要元素.其他的条件可以进行转化,从而转化为这三个要素间的关系.(2)准确求出已知函数式的导数、切线方程是解决此类问题的关键.1.思考辨析(1)若f (a )=a 3+2ax -x 2,则f′(a )=3a 2+2x . ( ) (2)⎣⎢⎡⎦⎥⎤C g (x )′=-Cg ′(x )g 2(x ). ( ) (3)任何函数都可以应用导数的运算法则求导数. ( )[提示] (1)√ (2)√(3)× 应用导数的运算法则求导数的前提是f (x ),g (x )均为可导函数,即f′(x ),g ′(x )存在.2.对于函数f (x )=e x x 2+ln x -2kx ,若f′(1)=1,则k 等于( ) A .e2 B .e3 C .-e 2D .-e 3A [∵f′(x )=e x (x -2)x 3+1x +2kx 2,第6页共11页∴f′(1)=-e +1+2k =1,解得k =e2,故选A.] 3.曲线y =sin x sin x +cos x -12在点M ⎝ ⎛⎭⎪⎫π4,0处的切线的斜率为( ) A .-12 B .12 C .-22D .22B [∵y ′=cos x (sin x +cos x )-sin x (cos x -sin x )(sin x +cos x )2=1(sin x +cos x )2,∴y ′|x =π4=12,∴曲线在点M ⎝ ⎛⎭⎪⎫π4,0处的切线的斜率为12.] 4.已知a 为实数,f (x )=(x 2-4)(x -a ),且f′(-1)=0,则a =________.12[∵f (x )=(x 2-4)(x -a )=x 3-ax 2-4x +4a ,∴f′(x )=3x 2-2ax -4. 又∵f′(-1)=3+2a -4=0, ∴a =12.] 5.设函数f (x )=13x 3-a2x 2+bx +c ,其中a >0,曲线y =f (x )在点P (0,f (0))处的切线方程为y =1,确定b 、c 的值.[解] 由题意,得f (0)=c ,f′(x )=x 2-ax +b ,由切点P (0,f (0))既在曲线f (x )=13x 3-a 2x 2+bx +c 上又在切线y =1上,得⎩⎨⎧f ′(0)=0,f (0)=1,即⎩⎪⎨⎪⎧02-a ×0+b =0,13×03-a 2×02+b ×0+c =1, 解得b =0,c =1.[基础达标练]第7页共11页1.已知函数f (x )=sin x +ln x ,则f ′(1)的值为( ) A .1-cos 1 B .1+cos 1 C .cos 1-1D .-1-cos 1B [∵f ′(x )=cos x +1x ,∴f ′(1)=cos 1+1.]2.函数f (x )=e x +x sin x -7x 在x =0处的导数等于( ) A .-6 B .6 C .-4D .-5A [∵f ′(x )=e x +(sin x +x cos x )-7, ∴f ′(0)=e 0+(sin 0+0)-7=-6.]3.设曲线y =x +1x -1在点(3,2)处的切线与直线ax +y +1=0垂直,则a 等于( )A .2B .12 C .-12 D .-2D [∵y =x +1x -1=1+2x -1, ∴y ′=-2(x -1)2.∴y ′|x =3=-12. ∴-a =2,即a =-2.]4.已知曲线y =x 3在点P 处的切线斜率为k ,则当k =3时的P 点坐标为( ) A .(-2,-8) B .(-1,-1)或(1,1) C .(2,8) D.⎝ ⎛⎭⎪⎫-12,-18 B [∵y ′=3x 2,k =3,∴3x 2=3,∴x =±1. 故P 点坐标为(-1,-1)或(1,1).] 5.已知点P 在曲线y =4e x+1上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( )第8页共11页A .⎣⎢⎡⎭⎪⎫0,π4B .⎣⎢⎡⎭⎪⎫π4,π2C .⎝ ⎛⎦⎥⎤π2,3π4D .⎣⎢⎡⎭⎪⎫3π4,πD [y ′=-4e x (e x +1)2=-4e x e 2x +2e x +1,设t =e x∈(0,+∞),则y ′=-4t t 2+2t +1=-4t +1t +2,∵t +1t ≥2,∴y ′∈[-1,0),α∈⎣⎢⎡⎭⎪⎫3π4,π.] 6.已知f (x )=13x 3+3xf ′(0),则f ′(1)=________.1 [由于f ′(0)是一常数,∴f ′(x )=x 2+3f ′(0),令x =0,则f ′(0)=0,∴f ′(1)=12+3f ′(0)=1.]7.若曲线y =x ln x 上点P 处的切线平行于直线2x -y +1=0,则点P 的坐标是________. (e ,e) [设P (x 0,y 0).∵y =x ln x , ∴y ′=ln x +x ·1x =1+ln x .∴k =1+ln x 0.又k =2,∴1+ln x 0=2,∴x 0=e. ∴y 0=eln e =e.∴点P 的坐标是(e ,e).]8.若函数f (x )=12x 2-ax +ln x 存在垂直于y 轴的切线,则实数a 的取值范围是________. [2,+∞) [∵f (x )=12x 2-ax +ln x , ∴f ′(x )=x -a +1x .∵f (x )存在垂直于y 轴的切线,∴f ′(x )存在零点, 即x +1x -a =0有解,∴a =x +1x ≥2.] 9.求下列函数的导数: (1)y =x ⎝ ⎛⎭⎪⎫x 2+1x +1x 3;(2)y =(x +1)⎝ ⎛⎭⎪⎫1x -1;第9页共11页(3)y =sin 4x 4+cos 4x4. [解] (1)∵y =x ⎝ ⎛⎭⎪⎫x 2+1x +1x 3=x 3+1+1x 2,∴y ′=3x 2-2x 3.(2)∵y =(x +1)⎝ ⎛⎭⎪⎫1x -1=-x 12+x -12,∴y ′=-12x -12-12x -32 =-12x ⎝ ⎛⎭⎪⎫1+1x . (3)∵y =sin 4x 4+cos 4x4=⎝ ⎛⎭⎪⎫sin 2x 4+cos 2x 42-2sin 2x 4cos 2x 4=1-12sin 2x 2=1-12·1-cos x 2=34+14cos x ,∴y ′=-14sin x .10.已知函数f (x )=ax 3+bx 2+cx 过点(1,5),其导函数y =f ′(x )的图象如图所示,求f (x )的解析式.[解] ∵f ′(x )=3ax 2+2bx +c , 又f ′(1)=0,f ′(2)=0,f (1)=5,∴⎩⎨⎧3a +2b +c =0,12a +4b +c =0,a +b +c =5,解得a=2,b =-9,c =12.第10页共11页∴f (x )的解析式是f (x )=2x 3-9x 2+12x .[能力提升练]1.设函数f (x )=sin θ3x 3+3cos θ2x 2+tan θ,其中θ∈⎣⎢⎡⎦⎥⎤0,5π12,则导数f ′(1)的取值范围是( )A .[-2,2]B .[2,3]C .[3,2]D .[2,2]D [由已知,得f ′(x )=sin θ·x 2+3cos θ·x ,所以f ′(1)=sin θ+3cos θ=2sin ⎝ ⎛⎭⎪⎫θ+π3,又θ∈⎣⎢⎡⎦⎥⎤0,5π12,所以π3≤θ+π3≤3π4,所以2≤2sin ⎝ ⎛⎭⎪⎫θ+π3≤2,所以2≤f ′(1)≤2.]2.下列图象中,有一个是函数f (x )=13x 3+ax 2+(a 2-1)x +1(a ∈R ,a ≠0)的导函数f ′(x )的图象,则f (-1)=( )A .13B .-13C .73D .-13或53B [∵f ′(x )=x 2+2ax +(a 2-1),∴导函数f ′(x )的图象开口向上.又a ≠0,∴f ′(x )不是偶函数,其图象不关于y 轴对称,∴f ′(x )的图象必为第三个图.由图象特征,知f ′(0)=0,∴a 2-1=0,且-a >0,∴a =-1,∴f (x )=13x 3-x 2+1,∴f (-1)=-13-1+1=-13.]3.设a ∈R ,函数f (x )=x 3+ax 2+(a -3)x 的导函数是f ′(x ),若f ′(x )是偶函数,则曲线y =f (x )在坐标原点处的切线方程为________.y=-3x[∵f(x)=x3+ax2+(a-3)x,∴f ′(x)=3x2+2ax+a-3.又f ′(-x)=f ′(x),即3x2-2ax+a-3=3x2+2ax+a-3对任意x∈R都成立,∴a=0,∴f ′(x)=3x2-3,f ′(0)=-3,∴曲线y=f(x)在坐标原点处的切线方程为y=-3x.]第11页共11页。



