计算动生电动势的方法

动生电动势计算公式动生电动势在电磁学中，动生电动势是由于磁场的改变而产生的电动势，根据法拉第电磁感应定律，动生电动势可以通过以下公式进行计算：1. 动生电动势的计算公式•动生电动势（ε） = -N * d(Flux)/dt其中， - ε表示动生电动势 - N表示线圈的匝数 - d(Flux)/dt 表示磁通量的变化率2. 动生电动势的举例解释旋转线圈中的动生电动势考虑一个简单的情况：一个线圈固定在旋转的磁场中。

当线圈旋转时，线圈中的磁通量会发生变化，从而产生动生电动势。

根据动生电动势的计算公式，可以得出以下结论：•动生电动势的大小与线圈的匝数成正比。

线圈匝数越多，动生电动势越大。

•动生电动势的大小与磁通量的变化率成正比。

磁通量的变化越快，动生电动势越大。

•动生电动势的方向遵循楞次定律。

根据楞次定律，产生的动生电动势的方向会阻碍磁场的变化。

磁铁掉入线圈中的动生电动势考虑另一个情况：一个磁铁从高处自由掉落并穿过一个线圈。

磁铁掉落过程中磁场的变化会导致动生电动势的产生。

通过动生电动势的计算公式，可以得出以下结论：•动生电动势的大小与线圈的匝数成正比。

线圈匝数越多，动生电动势越大。

•动生电动势的大小与磁通量的变化率成正比。

磁通量的变化越快，动生电动势越大。

•动生电动势的方向遵循楞次定律。

根据楞次定律，产生的动生电动势的方向会阻碍磁铁掉落的变化。

总结起来，动生电动势是由磁场的改变而产生的电动势，它可以通过公式ε = -N * d(Flux)/dt计算。

动生电动势的大小与线圈的匝数和磁通量的变化率成正比，而方向则遵循楞次定律。

动生电动势公式的推导及产生的机理摘要：在本文中，应用导数的知识推导出动生电动势在各种特殊情况下的表达形式，并进一步探究了动生电动势产生的机理。

揭示了产生动生电动势的实质是运动电荷在磁场中受到洛伦磁力的结果。

关键词：电磁感应定律；动生电动势；洛伦磁力法拉第电磁感应定律告诉我们，只要通过回路所围面积中的磁通量发生变化，回路中就会产生感应电动势。

由公式s B dSφ=⎰⎰可知，使磁通量发生变化的方法是多种多样的，但从本质上讲，可归纳为两类：一类是磁场保持不变，导体回路或导体在磁场中的运动；另一类是导体回路不动，磁场发生变化。

前者产生的感应电动势称为动生电动势，后者产生的电动势为感生电动势。

在本文中，主要对动生电动势公式的推导及其产生的机理作浅显的阐释。

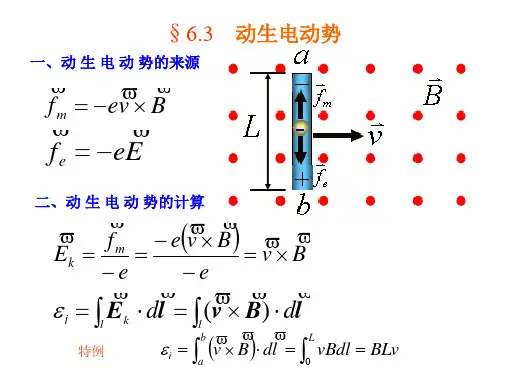
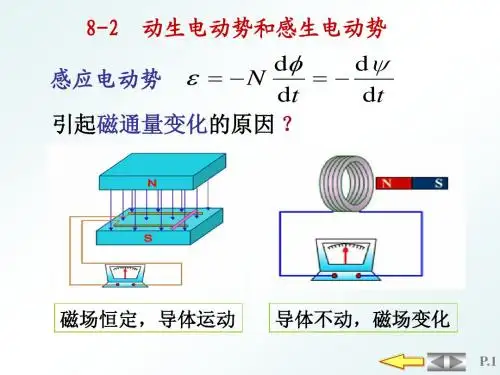
一、动生电动势在各种特殊情况下的表达形式在磁场保持不变的情况下，由于导体回路或导体运动而产生的感应电动势称为动生电动势（一）、在磁场中运动的导线内的动生电动势例1，如图1所示，一个由导线做成的回路ABCDA，其中长度为l的导线段AB在磁感应强度为B的匀强磁场中以速度V向右作匀速直线运动，AB、V和B 三者相互垂直，求运动导线AB段上产生的动生电动势。

解析：由题意可知，导线AB 、V 和B 三者相互垂直。

若在dt 时间内，导线AB 移动的距离为dx ，如右图所示，则在这段时间内回路面积的增量为dS ldx =。

如果选取回路面积矢量的方向垂直纸面向里，则通过回路所围面积磁通量的增量为：d ΦB S Bldx ==根据法拉第电磁感应定律知，导线AB 内所产生的感应电动势为[1]d Φε dt=- 其中，负号代表感应电动势的方向。

所以，在运动导线AB 段上产生的动生电动势的表达式为dx εBlv dtBl =-=-即运动导线AB 段上产生的动生电动势的大小为：Blv ，方向：B A →.例2、如图2所示，在方向垂直纸面向内的均匀磁场 B 中，一长为 l 的导体棒OA 绕其一端 O 点为轴，以角速度大小为ω逆时针转动，求导体棒OA 上所产生的动生电动势。

动生电动势公式3个公式
在基础电学中，我们学习过许多关于电路和电流的知识。

其中，电动势是理解电路中电流流动的重要概念之一。

在电路中，电动势可以用来表示电源的输出能力。

在本文中，我们将探讨三个常见的电动势公式以及其用途。

第一个公式是基本的电动势公式：
E = V - IR
其中，E表示电源的电动势，V表示电路中的电压，I表示电路中的电流，而R则表示电路中的电阻。

这个公式的用途是计算电源的电动势大小。

根据欧姆定律，电路的电流流动是受到电压和电阻的影响的，而电动势则可以被看做是电源的电压，衡量电源能给电路中的电流提供多少能量。

第二个公式是电动势与内阻的关系公式：
E = EM
F - Ir
这里，EMF代表电源的特征电动势，r则代表电源的内阻。

这个公式的用途在于计算电池的理论最大输出电动势。

其中，EMF代表电池在给定条件下的最大电动势，而r则代表电池内部的电阻。

通过这个公式，我们可以衡量电池的实际输出与其理论输出的差距。

第三个公式是洛伦兹力公式：
F = q(E + V x B)
这个公式与电动势的关系并不直接，它是用来计算电荷在磁场中受力的公式。

其中，F代表受力大小，q代表电荷，E代表电场强度，V 表示电荷流速，B则表示磁场强度。

在实际应用中，这个公式可以帮助我们设计电动机、发电机等机器。

通过以上三个电动势公式的介绍，我们可以看出，电动势在电路中扮演着非常重要的角色。

电动势公式的掌握可以帮助我们更好地理解电路和电流，进而解决实际问题。

希望本文能够为读者提供帮助！。

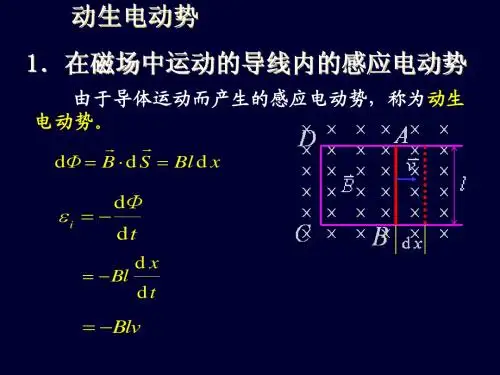
动生电动势的公式
动生电动势是指在一个固定的量子系统中，当外加电场和其它外
力施加了一个小变化时，核系统内部关联的变化。

它是一种可以用来
描述量子物理系统中特定状态转换时能量消耗的概念。

电场对本征态
的影响，通常用动生电动势公式来表示：V(r)=-∫E(r)*d(r), 其中
V(r)是动生电动势，E(r)是应用到波函数上的电场，D(r)是以r为自
变量的波函数积分。

另外，动生电动势也可以用来描述单子及其领域内电子的变化：
V(R)=−∫E(R)·d(R)，其中V(R)是动生电动势，E(R)是在波函数上施
加的电场，D(R)是以R为自变量的波函数积分。

在这种情况下，动生
电动势可以用来表达电子状态转换时电子原子结构及结合能等的变化。

动生电动势可以用来计算和分析物质的性质，如离子极化能、化
学键能、分子极化能等。

另外，也可以用来计算电子结构及光吸收、
电磁，热学等方面的性质。

最后，动生电动势也可以用来研究光学特性，如线谱强度、电离概率等，为材料科学的发展提供重要支持。

第32讲动生电动势()d i lv B lε=⨯⋅⎰整个导体回路均处于磁场中 i ()d bav B l ε=⨯⋅⎰对任意在磁场中运动的导体动生电动势：单纯由导体运动产生的感应电动势非静电力：f qv B=⨯洛非静电力场： E v B=⨯非静电求解运动导体中动生电动势的步骤： 3. 将动生电动势的矢量表示式化简为标量形式i ()d bav B lε=⨯⋅⎰i d ()d sin cos d v B l vB lεθα=⨯⋅=⋅1. 在运动导体上任取一线元； d l 2. 标出 处的和 矢量； B v d l 4.沿方向从导体的一端向另一端进行积分， 求得动生电动势的大小和方向。

d l i i 0,d 0,d l l εε><动生电动势方向与方向一致；动生电动势方向与方向相反。

动生电动势的方向如图所示，一根长度为 L 的铜棒，在均匀磁场中以匀角速度 ω 逆时针方向旋转， 的方向垂直铜棒的转动平面。

设 t = 0 时刻，铜棒与 Ob 的夹角为 θ ，则时刻 t 铜棒上的感应电动势为：(A) ωL 2B cos(ωt +θ)。

(B) ½ωL 2B cos(ωt +θ)。

(C) 2ωL 2B cos(ωt +θ)。

(D) ωL 2B 。

(E) ½ωL 2B 。

B × × × × × × × × × × × × × × × × × × × × × × × ×ω O L B b θ答案：（E ） i 0d L Bl l εω=-⋅⎰212BL ω=-v半径为 R 的金属圆板在均匀磁场中以角速度 ω 绕中心轴旋转，均匀磁场的方向平行于转轴，如图所示，这时板中由中心至同一边缘点的不同曲线上总感应电动势的大小 ，方向 。

三种动生感应电动势的计算方法
在我们日常生活中，动生感应电动势可以说是极其广泛的存在，在电子、化学、机械工程
等科学领域得到了广泛的应用，因此对于动生感应电动势的有效计算具有十分重要的意义。

一般来说，有三种常用的计算动生感应电动势的方法，它们分别是：数字计算方法、代数
计算方法和图形计算方法。

首先，数字计算方法是最常用的方法，其核心思想是通过建立一些数学模型来描述物理现象，然后利用数学软件来解这些数学模型，从而得到动生感应电动势的数值。

其次，代数计算方法是一种非常有效的计算动生感应电动势的方法，它的核心思想是将动
生感应电动势的问题转换为求解一个方程组的问题，这个方程组便会来描述动生感应电动
势的问题，从而可通过代数计算方法来求解动生感应电动势。

最后，图形计算方法也是求解动生感应电动势的一种不失效果的方法，核心思想就是通过
绘制图像来描述问题，然后利用图形求解软件来完成计算，从而求得动生感应电动势的值。

总之，以上三种动生感应电动势计算方法各有优势，任何一种方法都可以满足我们对自然
界动态变化特性描述的要求，但同时也有其不足之处，希望未来能更好地改进这种测量模型。

动生电动势的计算方法电动势是描述电池或发电机产生电流的能力的物理量，它是指单位时间内通过电池或发电机的电荷的能量。

计算电动势的方法可以分为两种，即理论计算和实验测量。

首先，我们来介绍理论计算电动势的方法。

理论计算通常基于电动势的定义公式：电动势=电场力/单位电荷。

其中，电场力是指单位电荷在电场中受到的力。

根据此定义，我们可以通过以下步骤计算电动势：1.确定电场强度：电场强度是指在电场中单位正电荷所受到的力的大小。

可以使用库仑定律计算电场强度，公式为：E=k*(Q/r^2)，其中，E表示电场强度，k表示库仑常数，Q表示电荷的大小，r 表示距离。

2.确定电场力：电场力是指电场中电荷所受到的力，可以使用公式F=q*E计算，其中，F表示电场力，q表示电荷的大小，E表示电场强度。

3.确定电动势：电动势可以通过电场力除以单位电荷来计算，公式为：ε=F/q。

这个结果就是电动势的数值。

以上是理论计算电动势的一般方法。

通过这种方法，我们可以简单地计算出电动势的数值，从而了解到电池或发电机产生电流的能力。

除了理论计算，我们还可以通过实验测量来确定电动势。

在实验中，一种常见的方法是使用伏特计来测量电动势。

伏特计是一种测量电压的装置，可以通过两个电极之间的电压差来测量电动势。

具体的实验步骤包括：1.将伏特计的正负极连接到电池或发电机的正负极上，确保电路完整。

2.读取伏特计上的数值，即为电动势的数值。

通过实验测量，我们可以更加直观地了解电池或发电机的电动势，并且可以验证理论计算的结果。

总而言之，计算电动势的方法有理论计算和实验测量两种方法。

理论计算可以通过电动势的定义公式来计算，而实验测量则可以使用伏特计来测量。

这两种方法都可以帮助我们全面了解电动势的概念和计算过程，为我们研究电池或发电机的能力提供指导意义。