空间群

+ ,- -, + +, - - ,+
+ ,- -, + +, - - ,+
+ ,- -, + +, - - ,+
俯视图(单胞)： (左)一般等效点位置 (右)对称元素分布
8 1 x,y,z; x,y,z; x,y,z; x,y,z;
x,y,z; x,y,z; x,y,z; x,y,z. 1 a mmm 0,0,0.
{R|} {R|t}、 {1|tn}、 {R|0} 、
点式空间群：由全部作用于同一个公共点
上的对称操作完全确定，或者说仅由点对称操 作和平移对称操作组合而产生。
۞ 螺旋轴或滑移面不是其基本操作。
۞ 点式空间群在单胞中一定至少有一个位置具有与
空间群点群相同的位置对称性
点对称条件
1(E)或1(i)
晶系
第十一讲—空间群(3)
第九讲 空间群(I)：点式空间群
晶体的宏观外形可视作一个连续整体的有限图形，而晶体 微观结构是不连续排列的原子在三维空间的无限展开。晶体 宏观对称性是晶体结构(原子排列对称性)即微观对称的反映。
点群中对称要素必须交于一点，只有方向的概念。微观对 称性中对称要素无须交于一点，要引入平移和位置的概念。
空间群：结晶学空间群就是能使三维周期物体(无
限大晶体)自身重复的所有几何对称操作的集合，
它构成数学意义上的群。
第十讲 空间群(II)：非点式对称操作
点对称操作：r’ = Rr r’=x’a + y’b +z’c r=xa + yb +zc 空间群操作：r’ = {R|t}r = Rr + t (赛兹算符)

空 间 群 可 分 为 230种
点式空间群(symmorphic space Group)
对称操作全部作用于同一个公共点上的，不包含任何一个比初基平移还要小的
平移τ。
73种
非点式空间群(Nonsymmorphic space Group)
157种
对称操作全部作用于同一个公共点上的，至少包含一个比初基平移还要小的平 移τ。
滑移面 由镜面和平移组合产生的对称元素称为滑移反映面，简称滑移面。滑移面的基本操作可表示为{m·t}， 其对称群为{m·t}p，P=0，±1，±2……。
晶体中有3种不同的滑移面，即轴向滑移、对角线滑移（又称n滑移）和金刚石滑移。 所有滑移中，都是经镜面操作后再平移单胞周期的某一分数的距离。和螺旋轴的操作相同，镜面和 平移两步操作的先后次序是不重要的。
以合适的取向放到阵点上的含义 如果希望每个阵点都具有正交对称性，那么放置物体时就必须使它的镜面和2次轴沿单胞某一轴方
向放置。这样导出的晶体结构，才会既有平移对称性又能使任何一个阵点都有C2v-mm2 的对称性。
这两种类型的对称操作正是描述整个晶体结构对称性的基本操作。
图 (a)是正交点阵的阵点上放上对称性 为C2v-mm2的物体的空间群的俯视图。
附图1
除了上述两种点群，我们不可能再增加任何对称操作而使 物体仍属于三斜晶系，所以，属于三斜晶系的晶类只有两种。 Ci-1点群的对称操作最多(不严格地说它具有最高的对称性)，称 这种点群为该晶系的全对称点群。
附图1
从上述两种点群的极射投影再一次说明在投影图上一般位置的正规点系的数目和点群具有对称操作 的数目相同，即与点群的阶数相同。
讨论点对称操作有哪些可能的组合方式，并对晶体做进一步划分。 3.1 群的概念和基本性质

的新对称操作，同样可由赛兹算符{RI}r=Rr+描述。晶体中有三
种不同的滑移面：轴滑移、对角n滑移、金刚石滑移。
轴向滑移：平移矢量平行于反映面，大小是单胞
轴长的一半。有a滑移、b滑移、c滑移；n滑移。
+
b
， +
a/2
+
+
b
+
b
b/2
_ ，
a/2
+
b/2
a/2
a/2
+
， +
b/2
b/2
a
a
a
n滑移 如 Pban
3
+ + + +
_ _ _ _
+ +
, ,
+ +
_ _
_ _
, ,
12 l
1
x,y,z; x,y,z; y,x,z; y,x,z;
y,x-y,z; y,x-y,z; x,y-x,z; x,y-x,z;
y-x,x,z; y-x,x,z; x-y,y,z; x-y,y,z.
x
, ,
Origin at 62m
Origin on 6
+
5/6+
1/3+ 1/2+ 2/3+ 1/6+ + 5/6+ 2/3+ 1/2+
1/3+ 1/6+ + 5/6+
Origin on 61
2/3+
P65 (C6, No. 170) P62 (C6, No. 171) P64 (C6, No. 172) P63 (C6, No. 173)

m[001]
|

1 2
,
1 2
,
0

r
金刚石滑移
空间群推导
点群
点阵 点阵对称性和点群的协调性
点式空间群 能否替换
用对应的非点式操作替换点式操作 非点式空间群
非点操作的位置
5种平面点阵
矩形 (a≠b, 90°)
平面群：
pm, pg, p2mg, p2mm 和 p2gg
• 立方结构的晶体，其原子一般位于高对称 的位置上，如Au，Al等金属单质
平面群（自学）
• 10种平面点群，13种点式平面群 • 有滑移面非点式对称操作，17种平面群
国际表
提供的信息的是： 1. 空间群的国际符号 2. Schoenflies符号 3. 晶系 4. 晶类 5。一般等效点图： 单胞的投影，包含所有等效点位置。
一般等效位置 确定单胞内的原子数及位置
商群中h个基本操作作用后产生h个一般等效点 系
点阵类型加一般等效点系描述空间群
等效位置确定商群的对称性及所属的晶系 由点阵类型便知道平移群的对称性
国际表中对称操作的表示
对称操作的分类及几何符号
由对称操作的矩阵求对应的几何符号
1，查表确定对应点对称操作 2，确定对称元素的取向和位置 a，反映 b，纯旋转 c，旋转倒反
• 空间群： 国际符号： 空间群符号的意义： 空间群的熊夫利推导方法：
符号的意义：第一个字符表示布拉菲点阵， 后面的表示对称性，符号的顺序与轴的选 取有关
空间群的两个重要内容：一般等效位置的坐 标，相对特定原点的全部对称元素
空间群与点群的关系：
• 俯视图 • 矩阵
空间群的描述
• 一般等效位置及对称元素

滑移反射
不对称单位先经镜面反射，然后沿平行与镜面的方向平移
滑移反射改变了不对称单位的手性。
滑移面分类
• 轴向滑移面：沿晶轴(a、b， c)方向滑移;
• 对角滑移面：沿晶胞面对角线或体对角线方向滑移，平 移分量为对角线一半;
• 金刚石滑移面：沿晶胞面对角线或体对角线方向滑移， 平移分量对角线1/4的对角滑移面。只有在体心或面心 点阵中出现，这时有关对角线的中点也有一个阵点，所 以平移分量仍然是滑移方向点阵平移点阵周期的一半。
Wyckoff位置 （2）
• 多重性（ multiplicity ）：告诉我们如果安 置一个特定原子在该位置，经过空间群的所 有对称操作，总共会产生多少个原子。 • 记号（ letter ）是从高对称性位置开始按英 文字母顺序指定的位置标记。 • 对称（ symmetry ）告诉我们原子所在之处 具有的对称元素。
空间群的描述
• 俯视图 • 矩阵 • 一般等效位置及对称元素
熊夫利推导230个空间群
• （1） 推导73个点式空间群 • （2） 分析可能的滑移面和螺旋轴 • （3) 把各种可能的布拉菲格子和h个点式 或非点式对称操作结合起来，推导可能的 非点式空间群
三斜晶系
单胞俯视图
新的反演中心是-1和单位平移操作组合而得
Wyckoff位置告诉我们在晶体中何处可以找到原子。
比如：单斜空间群Pm 仅有垂直于b轴的二个镜面。 一个在y = 0， 另一个在y = ½ 位置。 通过镜面操作，在x， y， z的原子 --〉在x， - y， z
第二个原子。如果我们安置原子在其中一个镜面(它的Y座标将必须是0
或½ )，镜面反射操作就不会产生第二个原子。
在非对称基元内任何一点不会再有对称 相关的位置

包括了这些与平移有关的操作之后，晶体的对称运动可以全部分类成230个对称操作群，称晶体空间群，也 称空间群。
的确定
如果知道了点群和点阵平移以外，还已知非晶格平移矢量，布拉维格子类型，则空间群就完全确定，列举出 所有可能的α和的相容性组合，就可得到所有可能的空间群。空间群共有230种，其中73种为简单空间群，余下 的157种为复杂空间群。
的三要素
非晶格平移矢量决定于与转轴相的坐标原点的选择，因此不是唯一的。 确定空间群必须指出的三个组成部分：
的表达
空间群符号(3张)表示一个空间群时，圣佛利斯符号和国际符号并用。
空间的国际群符号由两部分组成：前一部分是格子类型（布拉维格子）[P，C(A、B)，I，F]；后一部分与点 群的国际符号基本相同，不同的是那三个特定方向上的对称要素取自晶胞中对应方向上对称程度最高的那种对称 要素。
空间群的圣佛利斯符号是在其点群圣佛利斯符号的右上角加上序号即可。
谢谢观看
空间型和对称型（点群）体现了晶体内部结构的对称与晶体外形对称的统一。每个对称型有若干个空间群与 之相适应。即外形上属于同一对称型的晶体，其内部结构可分属于若干空间群。
空间群可以分为两类：一类称为简单空间群或称点空间群；一类称为复杂空间群或称非点空间群。
所谓点空间群，是由一个平移群和一个点群对称操作组合而成的，它的一般对称操作可以写成（R | t (αβγ)），其中R表示点群对称操作，t(αβγ)表示平移操作。具体分析表明，共有73种不同的点空间群。
点阵平移
理想的完整晶体应是无限大的，点阵单元在空间三个方向上的无限平移将给出整个点阵。或者说，无限的点 阵在平移下保持不变。所以平移也是一种对称操作，它的对称要素不是一个轴，一个点，一个面，而是整个点阵。 与平移有关的对称要素有三个：

正 交 222, mm2, mmm P
P222, C222, C I222, I F F222,
四 方 4, 4/m, 4mm, 422, P
4, 42m, 4/mmm
I
P4, P4/m, P4mm, P4/mmm, P422, P4, P42m, P4m2 I4, I4/m, I4mm, I4/mmm, I422, I4, I42m, I4m2
P 21 21 21
No.
19
½
+
_
P 212121 4 D2
¼ ¼ ¼
+
¼ ¼
½+
_
½+ ½
_
+
+
¼
Origin halfway between three pairs of non-intersecting screw axes
Number of positions, Wyckoff notation, and point symmetry
二次螺旋轴
平行于纸面
c/2 a/2或b/2 无
4 6
四次反演轴
六次旋转轴
三次旋转轴 三次螺旋轴 三次反演轴
c/3
2c/3 无
61 62 63 六次螺旋轴 64 65
3
6
六次反演轴
对称面符号
符号 对称面
图示符号
垂直于投影面 平行于投影面
滑移特征
没有(如果平面在z=1/4的 高度，就在符号边标注 1/4) 沿[100]滑移a/2，或沿[010] 滑移b/2，或沿<100>滑移
m a, b
反映面 (镜面)
轴滑移面
c n d
对角滑移面 (网)

空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

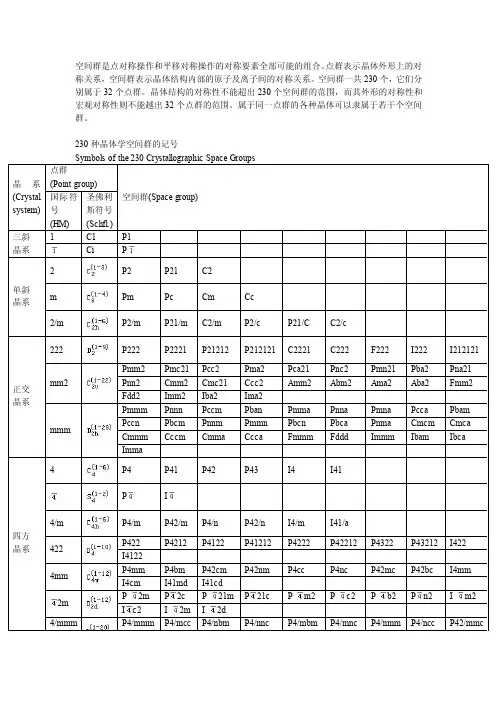
230种晶体学空间群的记号
Ci
I
2m
2m P P P I
m 1m P
m2 m2
m
3m 3m I P
Pm Im m
1 三斜晶系
2 单斜晶系
3 斜方晶系
4 四方晶系
为2，
为⊥m，5 三方晶系
6 六方晶系
(191) P6/mmm 7 等轴晶系。

矩阵乘法
1 0 0 x x 2次旋转矩 0 1 0 y y 阵 0 z z 0 1
倒反中心(Inversion center)
倒反中心：也称为反演中心或对称中心(Center of
0 cos sin 0 0 sin cos 0 1 0 0 1
旋转反映轴--映轴
旋转反映轴，简称映轴(rotoreflection axis)，其对 称操作是先进行绕映轴的旋转操作(n)后立刻再对
垂直于该映轴的反映面进行反映操作m。符号为ñ (Sn)，设对称轴沿[001]方向，其矩阵表示为：
Z Z
无， 2，m X 无， 2，m X
立方 2,m,4, `4
X
3,`3
体对 无， 2，m 面对 角线 角线
点群的Schönflies符号
Cn: 具有一个n次旋转轴的点群。
Cnh: 具有一个n次旋转轴和一个垂直于该轴的镜面的点群。
Cnv: 具有一个n次旋转轴和n个通过该轴的镜面的点群。 Dn: 具有一个n次旋转主轴和n个垂直该轴的二次轴的点群。 Sn:具有一个n次反轴的点群。 T:具有4个3次轴和4个2次轴的正四面体点群。
c)单位元素。 集合G中存在一个单位元素e，对任意元素， f G 有
ef fe f
d)可逆性。 对任意元素 f G ，存在逆元素 f 1 G ，使 f 1 f ff 1 e 则称集合G为一个群。
晶体学点群
晶体中满足群的性质定义的点对称操作的集合称
作晶体学点群。点对称操作的共同特征是进行操
非点式操作，如平移，螺旋转动和滑移反映。
对称操作和对称元素
对称操作：

空间群
简介
什么是空间群？
空间群是指空间中一组对称操作的所有可能组合，通常用来描述晶体的对称性。

在晶体学中，空间群是研究晶体结构和性质的重要工具。

空间群包含各种对称性操作，如旋转、镜像和平移等，以描述晶体的结构和排列方式。

历史
空间群的发展
空间群的概念最早可以追溯到19世纪初的晶体学研究。

科学家们发现晶体中
具有各种对称性操作，这些对称性操作可以基于不同的组合生成不同类型的空间群。

在随后的发展过程中，空间群的分类方法不断完善，以适应不同类型晶体的描述和研究需求。

分类
空间群的分类
空间群根据不同的对称性操作和组合方式可以被划分为不同类型。

常见的空间
群分类包括点群和空间群两大类。

点群描述了晶体中原子的对称性操作，而空间群则描述了晶体的整体对称性操作，包括旋转、平移和镜像等。

应用
空间群在材料科学中的应用
空间群在材料科学中有着广泛的应用。

通过研究晶体的空间群，科学家可以了
解晶体的结构和性质，为新材料的设计和合成提供重要参考。

空间群的研究也有助于解决材料的物理和化学性质之间的关联，推动材料科学领域的发展。

总结
结语
空间群作为描述晶体对称性的重要工具，在材料科学和晶体学领域发挥着重要
作用。

通过深入研究空间群的理论和应用，我们可以更好地理解晶体结构和性质的关系，为材料科学的进步和发展提供重要支持。

以上就是关于空间群的简要介绍，希望对您有所帮助。

种不同的滑移面：轴滑移、对角n滑移、金刚石滑移。
轴向滑移：平移矢量平行于反映面，大小是单胞
轴长的一半。有a滑移、b滑移、c滑移；n滑移。
+
b
， +
a/2
+
+
b
+
b
b/2
_ ，
a/2
+
b/2
a/2
a/2
+
， +
b/2
b/2
a
a
a
n滑移 如 Pban
左(中，右)图：沿b
(a, c) 滑移面的a (b, n)轴滑移
三方
3或3沿c 6或6沿c
2或2沿a、b和a+b 2或2沿a、b和a+b
2或2a、b和a+b 2或2a、b和a+b
六方
62m
63L23P) (Li
y
y
x
x
6m2 (Li63P3L2)
P62m (D3h, No. 189)
3
+ + + +
_ _ _ _
+ +
, ,
+ +
_ _
_ _
, ,
12 l
四次反演轴
六次旋转轴
三次旋转轴 三次螺旋轴 三次反演轴
c/3
2c/3 无
61 62 63 六次螺旋轴 64 65
3
6
六次反演轴
对称面符号
符号 对称面
图示符号
垂直于投影面 平行于投影面
滑移特征
没有(如果平面在z=1/4的 高度，就在符号边标注 1/4) 沿[100]滑移a/2，或沿[010] 滑移b/2，或沿<100>滑移

各个空间群晶胞与原胞的转换
空间群与晶胞、原胞的转换是一个复杂的过程，涉及到晶体学和空间几何的知识。

以下是一些基本的概念和步骤：
1.了解空间群：空间群是描述晶体内部结构对称性的基本对称元素。

空间群可以用符号表示，例如
Pm3m、P4/mmm等。

每个空间群都有一组特定的对称元素，如镜面、旋转轴、反轴等。

2.确定晶胞参数：晶胞是晶体结构的基本单元，由三个互相垂直的向量a、b、c和一个角度θ表示。

晶胞参数包括晶格常数a、b、c和α、β、γ等角度。

3.确定原胞参数：原胞是比晶胞更小的单位，是晶胞的一部分。

原胞的参数与晶胞相同，但可以包
含更多的原子或分子。

4.空间群的转换：通过特定的变换操作可以将晶胞参数和原胞参数转换为不同的空间群。

这些变换
操作包括旋转、镜面反射、反轴等。

5.确定原胞中的原子或分子：在确定了原胞参数后，可以根据空间群的对称性确定原胞中的原子或
分子的位置。

这通常涉及到对原胞进行平移、旋转或镜面反射等操作。

需要注意的是，空间群与晶胞、原胞的转换是一个复杂的过程，需要深入了解晶体学和空间几何的知识。

在进行具体的转换操作时，建议参考相关的专业书籍或咨询专业人士的意见。

空间群（Space group）是一种描述晶体结构的数学工具，它把晶体中的所有原子看作点，并使用符号（由数字和符号组成）来表示这些点的几何排列。

空间群的种类非常多，通常在几千种以上，但常用的只有几十种。

以下是一些常用的空间群符号及其含义：
1. 225型空间群（P22_1_5）：这种空间群表示具有两套相互垂直的近正方形的简单晶体结构，每个原子都在一个平面上，通过角顶相互连接。

2. 432型空间群（P4_3_2）：这种空间群表示具有四套相互垂直的矩形排列的简单晶体结构，每个原子都在一个平面上，通过角顶相互连接。

3. 62型空间群（I6_2）：这种空间群表示具有六套相互垂直的六边形排列的复杂晶体结构，每个原子都在一个平面上，通过角顶相互连接。

4. 61型空间群（P6_1）：这种空间群表示具有六套相互垂直的六边形排列的简单晶体结构，每个原子都在一个六边形的顶点上。

5. 31型空间群（P3_1）：这种空间群表示具有三套相互垂直的平面排列的简单晶体结构，每个原子都在一个平面上。

需要注意的是，空间群的种类非常多，不同文献和教科书可能会对同一晶体的空间群描述有所不同。

因此，在进行晶体结构分析时，需要参考具体的文献或教科书来确定具体的空间群符号和含义。

此外，不同的晶体结构也可能需要不同的计算参数和方法，因此在应用空间群进行晶体结构分析时需要选择适当的软件和算法。

目前常用的晶体结构分析软件如VESTA、Pymatgen等都提供了对空间群的详细解释和使用方法。

以上就是部分常见的空间群符号及含义，如果您需要了解更多空间群的符号及含义，建议您查阅相关的专业书籍或咨询专业人士。

空间群在文章中的表达形式1.引言【1.1 概述】空间群是固体结构中的一种重要组织形式，它描述了晶体中的原子或分子在空间中的排列方式和周期性。

空间群在材料科学、化学、物理学以及生物学等领域都有广泛的应用。

在科学研究和工程实践中，了解和掌握空间群的定义、特点和表示方法对于分析和设计晶体结构至关重要。

空间群的定义与特点是我们理解和研究该概念的基础。

在晶体学中，空间群是指所有保持晶格不变的空间对称操作的集合。

这些对称操作包括平移、旋转、镜面反射等，可通过数学表达式进行描述。

每个空间群都具有一些独特的特点，如对称性的类型、晶体的点群和晶胞的形状等。

空间群的特点直接决定了晶体的物理性质和结构稳定性。

空间群的分类与表示方法是研究和表达空间群的重要手段。

根据国际晶体学联合会（International Union of Crystallography, IUCr）的分类法，空间群可以分为230个不同的类型。

这些类型根据空间群的对称性和操作方式进行划分，每个类型都有一个特定的编号和名称。

此外，空间群还可以用不同的表示方法进行描述，如赝空间群、世界坐标系下的坐标变换等。

这些表示方法方便了晶体学家和科研人员对空间群进行研究和应用。

本文将全面介绍空间群在文章中的表达形式。

首先，我们将详细探讨空间群的定义与特点，帮助读者全面了解空间群的基本概念及其作用。

然后，我们将介绍空间群的分类与表示方法，以便读者能够有效地区分和辨识不同类型的空间群。

最后，我们将讨论空间群在文章中的重要性以及不同表达形式对文章的影响。

通过本文的阅读，读者将能够更好地理解和运用空间群的概念，为相关科研和实践提供有力支持。

1.2 文章结构文章结构部分的内容如下：文章结构是指文章的整体框架和组织方式。

一个好的文章结构可以使读者更好地理解文章的内容，帮助作者清晰地表达思想和观点。

本文的结构分为引言、正文和结论三个部分。

引言部分主要包括概述、文章结构和目的三个方面。

国际符号international symbol 采用国际符号，不仅可以表示出各种晶类中有那些对称元素，而且还能表示出这些对称元素在空间的方向。

国际符号根据各种晶类的对称性可以是三项、或二项、或一项符号组成，它分别表示晶体某三个、或二个、或一个方向上的对称元素。

如果在某一个方向上，同时具有对称轴和垂直于此轴的对称面，则写成分数形式。

熊夫利斯（Sch öenfles ）符号C n ：字母表示旋转的意思，组标n 表示旋转的次数，n=1、2、3、4、6。

例如C 2代表二次旋转轴。

C nh ：表示除了n 次旋转轴外，还包括一个与此轴垂直的对称面。

C nv ：表示除了n 次旋转轴外，还包括一个与此轴重合（即平行）的对称面。

C ni ：表示除了n 次旋转轴外，还包括一个对称中心。

C i：表示有一个对称中心。

S4：表示有一个四次旋转倒反轴。

D n：表示除了n次主旋转轴外，还包括n 个与之轴垂直的二次旋转轴。

D nh：表示除了D n的对称性外，还包括一个与主旋转轴垂直的对称面，和n个与二次旋转轴重合（即平行）的对称面。

D nd：表示除了D n的对称性外，还包括n个T：除了四个三次旋转轴外，还包括三个正交的二次旋转轴。

T h：除了T的对称性外，还包括与二次旋转轴垂直的三个对称面。

T d：除了T的对称性外，还包括六个平分两个二次旋转轴夹角的对称面。

O：包括三个互相垂直的四次旋转轴，六个二次旋转轴，和四个三次旋转轴。

O h：除了O的对称性外，还包括T d与T h的对国际符号与熊氏符号对比国际符号熊氏符号1C 12C 23C 34C 46C 6m C sC i ，S 2S 14其它注意事项由于分子没有无限周期性的限制，所以分子点群的数目要多于晶体中的点群数目32个； 自然界对称性很多，例如：五度对称性，足球，富勒烯C 60,buckministerfullerence ，碳管小结summary密勒指数（Miller indices）对称元素和对称操作晶体的三十二个点群对称性和点群对于压电铁电体非常重要！ 只有晶体才会有压电铁电性，不存在非晶压电铁电体。

空间群转换与等效点 系
目录
• 空间群转换的基本概念 • 等效点系的定义与性质 • 空间群转换与等效点系的关系 • 空间群转换的实例分析 • 总结与展望
01
空间群转换的基本概念
空间群的定义
空间群是晶体中所有等同的晶格 点在空间中的对称变换集合。
空间群描述了晶体中原子或分子 的排列规律，以及这些原子或分
加强跨学科合作
加强物理学、化学、材料科学、数学等学科之间的合作， 共同推进空间群转换与等效点系的研究，促进相关领域的 交叉融合发展。
THANKS
感谢观看
等效点系中的等效原子或分子的位置可以相互替 代，且不会改变晶体的结构和性质。
等效点系在晶体结构中具有周期性和规律性，是 描述晶体结构周期性和对称性的基础。
等效点系的应用
等效点系在晶体结构分析和晶体材料研究中具有广泛的应用，是描述晶体结构和性 质的重要工具。
等效点系可以用于确定晶体的空间群和对称性，进而研究晶体的物理和化学性质。
未来研究方向与展望
拓展应用领域
进一步探索空间群转换与等效点系在材料科学、物理学、 化学等领域的应用，挖掘其在新型材料、新能源等领域的 应用潜力。
发展计算模拟方法
结合计算科学和人工智能技术，发展高效、精确的晶体结 构预测和性质计算方法，为实验和应用提供更准确的指导 。
深化理论基础
深入研究空间群转换与等效点系的数学和物理学基础，完 善相关理论体系，为未ห้องสมุดไป่ตู้的研究提供更坚实的支撑。
1 2 3
促进晶体学和材料科学的发展
空间群转换与等效点系的研究有助于深入理解晶 体结构和性质，为材料科学的发展提供重要的理 论支撑。
指导实验与应用
通过空间群转换与等效点系的研究，可以预测和 解释实验中观察到的晶体结构和物理性质，为实 际应用提供指导。

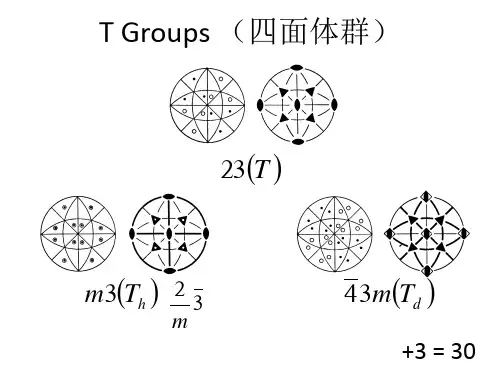
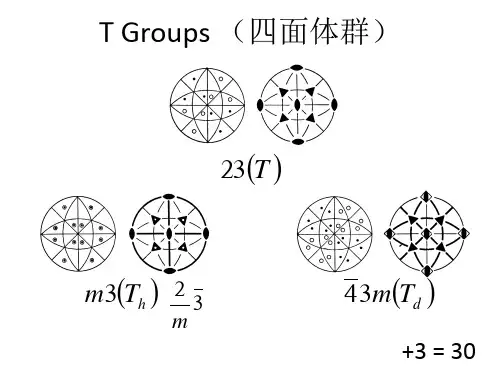
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups晶系(Cry stal syste m) 点群(Pointgroup)空间群(Space group) 国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1 C1 P1Ci P单斜晶系2 P2 P21 C2m Pm Pc Cm Cc2/m P2/mP21/mC2/m P2/c P21/C C2/c正交晶系222 P222P2221P21212P212121C2221C222 F222 I222I212121 mm2Pmm2Pmc21Pcc2 Pma2 Pca21 Pnc2Pmn21Pba2 Pna21 Pnn2Cmm2Cmc21Ccc2Amm2Abm2Ama2Aba2 Fmm2 Fdd2Imm2Iba2 Ima2mmmPmmmPnnn Pccm Pban Pmma Pnna Pmna Pcca Pbam PccnPbcmPnnmPmmnPbcn Pbca PnmaCmcmCmca CmmmCccmCmmaCccaFmmmFdddImmmIbam Ibca Imma四方晶系4 P4 P41 P42 P43 I4 I41P I4/m P4/m P42/mP4/n P42/n I4/m I41/a422 P422P4212P4122P41212P4222P42212P4322P43212I422 I41224mm P4mmP4bmP42cmP42nmP4cc P4ncP42mcP42bcI4mm I4cmI41mdI41cd2m P2mP2cP21mP21cPm2Pc2Pb2Pn2Im2 I c2I2mI2d4/m mm P4/mmmP4/mccP4/nbmP4/nncP4/mbmP4/mncP4/nmmP4/nccP42/mmc P42/mcmP42/nbcP42/nnmP42/mbcP42/mnmP42/nmcP42/ncmI4/mmmI4/mcmI41/amdI41/acd三方晶系3 P3 P31 P32 R3P R32 P312 P321 P3112P3121P3212P3221R32 3m P3m1P31mP3c1 P31c R3m R3cmP1mP1cPm1P c1RmR c六方晶系6 P6 P61 P65 P62 P64 P63P6/m P6/mP63/m622 P622P6122P6522P6222P6422P63226mmP6mmP6ccP63cmP63mcm2Pm2Pc2P2mP2c6/mmmP6/mmmP6/mccP63/mcmP63/mmc立方23 P23 F23 I23 P213 I213晶系m Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3432 P432 P4232F432F4132I432P4332P4132I41323m P3mF3mI3m P3nF3cI3dm m PmmPnnPmnPnmFmmFmcFdmFdcImm Ia d1 三斜晶系(Triclinic)点群空间群对称要素方位关系1 1 (1) P12 -1 (2) P-12 单斜晶系(Monoclinic) b为唯一轴点群空间群对称要素方位关系3 2 (3) P2(4) P21(5) C2b为2次轴或21螺旋轴4 m (6) Pm(7) Pc(8) Cm(9) Cc b为⊥m5 2/m (10) P2/m(11) P21/m(12) C2/m(13) P2/c(14) P21/c(15) C2/c b为2+⊥m3 斜方晶系(Orthohombic) 三个方位：a，b，c点群空间群对称要素方位关系6 222 (16) P222(17) P2221(18) P21212(19) P212121(20) C2221(21) C222(22) F222(23) I222(24) I212121 abc皆为27 mm(mm2)(26) Pmc21 (27) Pcc2 (28) Pma2 (29) Pca21 (30) Pnc2 (31) Pmn21 (32) Pba2 (33) Pna21 (34) Pnn2 (35) Cmm2 (36) Cmc21(37) Ccc2 (38) Amm2 (39) Abm2 (40) Ama2 (41) Aba2 (42) Fmm2 (43) Fdd2 (44) Imm2 (45) Iba2 (46) Ima2a 为⊥m ，b 为⊥m ，c 为2（两两垂直的对称面交线为2）。