推荐-文科训练4 精品

1.〔此题总分值14 分〕设数列a的前n项和为S n,且S n4a n3(n1,2,)，n〔1〕证明: 数列a n是等比数列；〔2〕假设数列b满足b n1a n b n(n1,2,)，b12，求数列b n的通项公n式．2.〔本小题总分值12分〕等比数列a的各项均为正数，且n2 2a3a1,a9aa.123261.求数列a n的通项公式.2.设blogaloga......loga,求数列n31323n 1bn的前项和.3.设数列a满足n2n1 a12,a1a32nn〔1〕求数列a的通项公式；n〔2〕令b n na n，求数列的前n项和S n3.等差数列{a n}的前3项和为6，前8项和为﹣4．〕，求数列{b n}的前n项和S n．〔Ⅰ〕求数列{a n}的通项公式；n﹣1*〔Ⅱ〕设b n=〔4﹣a n〕q〔q≠0，n∈N× 5.数列{a n}满足，，n∈N．〔1〕令b n=a n+1﹣a n，证明：{b n}是等比数列；〔2〕求{a n}的通项公式．...4.解：〔1〕证：因为S n4a n3(n1,2,)，那么S n14a n13(n2,3,)，所以当n2时，a SS14a4a1，nnnnn4整理得aa1．5分nn3由S43，令n1，得a14a13，解得a11．n an所以分a是首项为1，公比为n43的等比数列．7〔2〕解：因为4n1 a()，n3由b1ab(n1,2,)，得nnn4n1 bb()．9分n1n3由累加得()()()b n bbbbbbb12`132nn14n11()43n1＝23()1，〔n2〕，43134n1 当n=1时也满足，所以)1b3(．n35.解：〔Ⅰ〕设数列{a n}的公比为q，由 2a39a2a6得32a39a4所以21q。

有条件9可知a>0,故1q。

311a。

故数列{a n}的通项式为a n=33由2a13a21得2a13a2q1，所以1n。

〔Ⅱ〕b logaloga...logan111111(12...n)n(n1)2故12112() bn(n1)nn1n111111112n ...2((1)()...()) bbb223nn1n1 12n...所以数列1{}bn2n 的前n 项和为n16.解：〔Ⅰ〕由，当n≥1 时，a1[(a1a)(a a1)(a2a1)]a1nnnnn2n12n33(222)222(n1)1。

高三文科数学考前训练（四）一、选择题（5×10=50分）1．复数22ii+-(i 是虚数单位)表示复平面内的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．函数1()3f x x =-的定义域是（ ）A ．[2,)+∞B ．[2,3)C ．(,3)(3,)-∞⋃+∞D ．()[2,3)3,⋃+∞ 3． 已知等差数列b a ,,1，等比数列5,2,3++b a ，则该等差数列的公差为（ ） A ．3或3-B ．3或1-C ．3D ．3-4．把函数sin y x =的图象上所有点的横坐标缩小到原来的一半，纵坐标保持不变，再把所得函数图象向左平移4π个单位长度，得到的函数图象对应的解析式是（ ）A ．cos2y x =B ．sin 2y x =-C ．sin(2)4y x π=-D ．sin(2)4y x π=+5．某几何体的俯视图是如右图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形，则该几何体的表面积为（ ）A ．80B ．88224+C ．40224+D ．1186．函数()sin cos()6f x x x π=-+的单调递增区间为（ ）A ．7[2,2]()66k k k Z ππππ--∈ B ．5[2,2]()66k k k Z ππππ-+∈ C ．4[2,2]()33k k k Z ππππ--∈ D ．2[2,2]()33k k k Z ππππ-+∈ 7．如图，平行四边形ABCD 中，2,1,60AB AD A ==∠=，点M 在AB 边上，且13AM AB DM DB =⋅，则等于（ ）A． BC ．1-D ．1 8．已知抛物线24x y =-的准线与双曲线22221(0,0)y x a b a b-=>>的两条渐近线围成一个等腰直角三角形，则该双曲线的离心率是（ ） A ．2 BCD ．59．一艘海轮从A 处出…发，以每小时40海里的速度沿东偏南50°方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是东偏南20°，在B 处观察灯塔，其方向是北偏东65°，则C B 、两点间的距离是（ ） A ．102海里B ．103海里C ．202海里D ．203海里10．在R 上定义运算⊗：)1(y x y x -=⊗．若对任意2>x ，不等式2)(+≤⊗-a x a x 都成立，则实数a 的取值范围是（ ）A ．[]7,1-B ．(]3,∞-C ．(]7,∞-D ．(][)+∞-∞-,71,二、填空题（5×5=25分）11．某班50名学生在一次健康体检中，身高全部介于155cm 与185cm 之间．其身高频率分布直方图如图所示． 则该班级中身高在[]185,170之间的学生共有 人． 12．已知圆C 经过点(0,3)A 和(3,2)B ,且圆心C 在直线y x =上,则圆C 的方程为13．设变量,x y 满足约束条件22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩，则11y s x +=+的取值范围是14．阅读右面的程序框图，则输出的S 等于 15．下列命题正确的序号为 . ①函数)3ln(x y -=的定义域为]3,(-∞;②定义在],[b a 上的偶函数b x a x x f +++=)5()(2最小值为5;③若命题:p 对R x ∈∀，都有022≥+-x x ，则命题:p ⌝R x ∈∃，有022<+-x x ;④若0,0>>b a ，4=+b a ，则ba 11+的最小值为1. 三、解答题（75分）16．（本题满分13分）已知平面向量(sin,cos)44x x ππ==a b 错误！未找到引用源。

宜昌市第一中学2015届高三年级文科综合训练卷（四）考试时间：2015年1月8日 7:55-10:25第Ⅰ卷(选择题，140分)本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

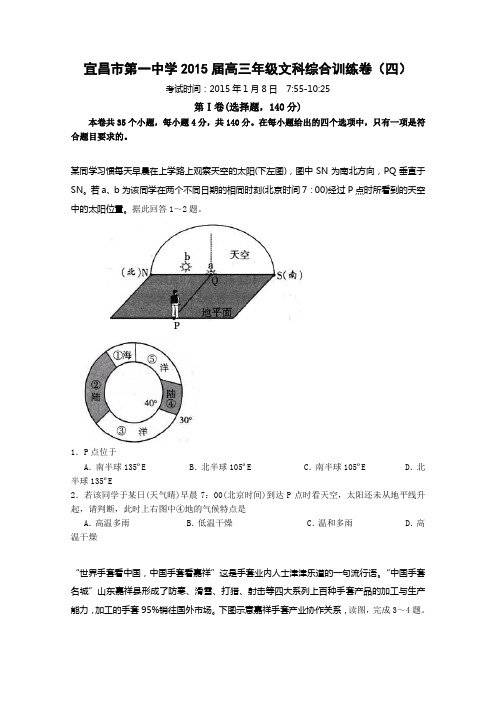
某同学习惯每天早晨在上学路上观察天空的太阳(下左图)，图中SN为南北方向，PQ垂直于SN。

若a、b为该同学在两个不同日期的相同时刻(北京时间7：00)经过P点时所看到的天空中的太阳位置。

据此回答1～2题。

1．P点位于A．南半球135ºE B．北半球105ºE C．南半球105ºE D．北半球135ºE2．若该同学于某日(天气晴)早晨7：00(北京时间)到达P点时看天空，太阳还未从地平线升起，请判断，此时上右图中④地的气候特点是A．高温多雨 B．低温干燥 C．温和多雨 D．高温干燥“世界手套看中国，中国手套看嘉祥”这是手套业内人士津津乐道的一句流行语。

“中国手套名城”山东嘉祥县形成了防寒、滑雪、打猎、射击等四大系列上百种手套产品的加工与生产能力，加工的手套95%销往国外市场。

下图示意嘉祥手套产业协作关系，读图，完成3～4题。

3．数百家手套生产加工及配套企业，形成了以县城为中心，以重点乡镇为依托，向全县多数乡村辐射传导的发展格局，大量手套企业集聚有利于A．共同利用基础设施，加强交流协作 C．增强集聚优势，实现产业升级B．降低工人工资，增加利润 D．降低生产成本，提高批发价格4．嘉祥手套产业的协作关系对当地的影响是A．削弱同类企业间的竞争 B．提高区域竞争力C．限制了其它产业的发展 D．降低专业化程度下图为某区域1月某日24小时内不同时刻海平面气压分布示意图，四幅图的等压距均为2.5百帕。

读图完成5～7题。

5．根据天气系统的发展过程，四幅天气图的先后排序为A．③④②① B．④③②① C．①④②③ D．②①④③6．形成图中雨区降水的主要天气系统是A．冷锋 B．暖锋 C．反气旋 D．高压7．关于图示区域大气状况的叙述，正确的是A．甲地在①时刻风力最大 B．该日甲地风向发生显著变化C．甲地气温随天气系统移动而上升 D．雨区降水形式可能为暴雪“花环式”海流发电站是用一串螺旋桨组成的，它的两端固定在浮筒上，浮筒里装有发电机。

2023届高三一轮复习联考（四）全国卷8．已知函数J(x)＝屈s in(2x+0)—cos(2x+0),0 E（气］，且f(O)=l，则0=re_6．A产4．B亢＿3．c产2．D文科数学试题注意事项：l．答卷前，考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交 回。

考试时间为120分钟，满分150分一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={x lx2<l},B = {x I O<x<2}，则AnB=A.(—1, 2)2.(2+i)(2—3i)=A.l—i3．下列命题中的假命题是迈A.3 x E R, s in x=— 2A.—2B.25．函数f(x)=cos x+sin 2x的图象可能是yB.(—1,0)B.7—IyC.(O, 1)C.l—4iB.3 xER,ln x=—lC.'efxER,x2>0D.'efxER,3气＞04．已知数列{a n}是各项均为正数的等差数列，a s=10，且a4• a6=96，则公差为C.—2或2D.4y yAXB c D16．已知a=lg—,b=cos l,c=z-2，则a,b,c的大小关系为2A.a<b<cB.a<c<bC.b<a<cxD.Cl,2)D.7—4iD.b<c<a.,7．如图，正方形ABCD中，E、F分别为AB、A D的中点，且BF＝入B E+AXDµBD，则入十µ的值是1 EA.1B.—23D.2C.—2 B CX 2 y 2 ＇，9直线l:y＝瓦x与椭圆C:勹+—=1交于P,Q两点，F是椭圆C的右焦点，且PP·QF=a z, b20，则椭圆的离心率为A.4—2祁B.2点—3C．点—l10．已知正数a,b满足矿＋2矿＝1，则a矿的最大值是A. 屈屈B. C.— D.—11如图所示，在正方体ABCD—A1B1C卫中，O,F分别为BD,AA]的中D,点，设二面角F—D10—B的平面角为a直线O F与平面B B丸D所成A,＇\ \B角为p，则::;：三：高三三三三：三＜言昙三三：个立体，被任一平行千这两个平面的平面所截，如果两个截面的面积相等，则这两个几何体的体积相等．上述原理在中国被称为祖睢原理，国外则一般称之为卡瓦列利原理．已知y将双曲线C：三——=1与直线y＝土2围成的图形绕y轴8 2旋转一周得到一个旋转体E，则旋转体E的体积是昼2D二、填空题：本题共4小题，每小题5分，共20分。

[A卷]1．(2021·宁波市高三模拟) 用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是()解析：选B.由题意知，用平行于水平面的平面去截球所得的底面圆是看不见的，所以在俯视图中该部分应当是虚线圆，结合选项可知选B.2．下列命题中，错误的是()A．圆柱的轴截面是过母线的截面中面积最大的一个B．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台C．圆台的全部平行于底面的截面都是圆D．圆锥全部的轴截面都是全等的等腰三角形解析：选B.依据棱台的定义，用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．3．(2021·台州市高三调考)一个空间几何体的三视图如图所示，其体积为()A．16B．32C．48 D．96解析：选A.由题意作出直观图P-ABCD如图所示，则该几何体是一个四棱锥，底面是一个直角梯形，其面积为12×(2＋4)×4＝12，高为4，因此其体积V＝13×12×4＝16.4．(2021·高考全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r＝()A．1 B．2C．4 D．8解析：选B.如图，该几何体是一个半球与一个半圆柱的组合体，球的半径为r，圆柱的底面半径为r，高为2r，则表面积S＝12×4πr2＋πr2＋4r2＋πr·2r＝(5π＋4)r2.又S＝16＋20π，所以(5π＋4)r2＝16＋20π，所以r2＝4，r＝2，故选B.5．如图是一个体积为10的空间几何体的三视图，则图中x的值为()A．2 B．3C．4 D．5解析：选A.依据给定的三视图可知，该几何体对应的直观图是一个长方体和四棱锥的组合体，所以几何体的体积V＝3×2×1＋13×3×2×x＝10，解得x＝2.故选A.6. 如图，水平放置的三棱柱的侧棱长为1，且侧棱AA1⊥平面A1B1C1，正视图是边长为1的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为()A．2 3 B． 3C.32D．1解析：选C.由直观图、正视图以及俯视图可知，侧视图是宽为32，长为1的长方形，所以面积S＝32×1＝32.故选C.7．一平面截一球得到直径为2 5 cm的圆面，球心到这个平面的距离是2 cm，则该球的体积是() A．12πcm3B．36πcm3C．646πcm3D．108πcm3解析：选B.由于球心和截面圆心的连线垂直于截面，由勾股定理得，球半径R＝22＋（5）2＝3，故球的体积为43πR3＝36π(cm3)．8．(2021·石家庄市第一次模拟)一个几何体的三视图如图所示，则该几何体的体积是()A．64B．72C．80D．112解析：选B.由三视图可知该几何体是一个组合体，下面是一个棱长为4的正方体；上面是一个三棱锥，三棱锥的高为3.故所求体积为43＋13×12×4×4×3＝72.9．已知某组合体的正视图与侧视图相同(其中AB＝AC，四边形BCDE为矩形)，则该组合体的俯视图可以是________(把正确的图的序号都填上)．解析：几何体由四棱锥与四棱柱组成时，得①正确；几何体由四棱锥与圆柱组成时，得②正确；几何体由圆锥与圆柱组成时，得③正确；几何体由圆锥与四棱柱组成时，得④正确．答案：①②③④10．把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1∶4，母线长是10 cm，则圆锥的母线长为________ cm.解析：作出圆锥的轴截面如图，设SA＝y，O′A′＝x，利用平行线截线段成比例，得SA′∶SA＝O′A′∶OA，则(y－10)∶y＝x∶4x，解得y＝403.所以圆锥的母线长为403cm.答案：40311．(2022·高考课标全国卷Ⅱ改编)正三棱柱ABC-A1B1C1的底面边长为2，侧棱长为 3，D为BC中点，则三棱锥A­B1DC1的体积为________．解析：由题意可知AD⊥BC，由面面垂直的性质定理可得AD⊥平面DB1C1，又AD＝2sin 60°＝3，所以V A­B1DC1＝13AD·S△B1DC1＝13×3×12×2×3＝1，故选C.答案：112．一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图所示，则该四棱锥的侧面积为________，体积为________．解析：由题意可知该四棱锥为正四棱锥，底面边长为2，高为2，侧面上的斜高为22＋12＝5，所以S 侧＝4×⎝⎛⎭⎫12×2×5＝45，V＝13×22×2＝83.答案：458313．(2021·南昌市第一次模拟)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1内一点，则三棱锥P -BCD 的正视图与侧视图的面积之比为________．解析：依据题意，三棱锥P -BCD 的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高，侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高，故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1. 答案：1∶114．如图是某空间几何体的三视图，则该几何体的体积为________．解析：由三视图可知，该几何体是棱长为2，2，1的长方体挖去一个半径为1的半球，所以长方体的体积为2×2×1＝4，半球的体积为12×43π×13＝2π3，所以该几何体的体积是4－2π3.答案：4－2π315．如图，正方体ABCD -A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1­EDF的体积为________．解析：由于B 1C ∥平面ADD 1A 1，所以F 到平面ADD 1A 1的距离d 为定值1，△D 1DE 的面积为12D 1D ·AD ＝12，所以V D 1­EDF ＝V F ­D 1DE ＝13S △D 1DE ·d ＝13×12×1＝16.答案：16[B 卷]1．一个锥体的正视图和侧视图如图所示，下面选项中，不行能是该锥体的俯视图的是( )解析：选C.依据三视图中“正俯长一样，侧俯宽一样，正侧高一样”的规律，C 选项的侧视图宽为32，不符合题意，故选C.2．(2021·邢台市摸底考试)已知一个几何体的三视图是三个全等的边长为1的正方形，如图所示，则该几何体的体积为( )A.16 B.13 C.23D ．56解析：选D.依题意得，题中的几何体是从棱长为1的正方体ABCD -A ′B ′C ′D ′中截去三棱锥A ′­ABD 后剩余的部分，因此该几何体的体积等于13－13×⎝⎛⎭⎫12×12×1＝56，故选D. 3．(2022·高考湖南卷)一块石材表示的几何体的三视图如图所示．将该石材切削、打磨，加工成球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4解析：选B.由三视图可知该几何体是一个直三棱柱，如图所示．由题意知，当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆相同时，该球的半径最大，故其半径r ＝12×(6＋8－10)＝2.因此选B.4．(2021·高考山东卷)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B ．4π3 C.5π3D ．2π 解析：选C.过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB 2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3，故选C.5．(2021·郑州市第一次质量猜测)某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy 的最大值为( )A ．32B ．327C ．64D ．647解析：选C.依题意，题中的几何体是三棱锥P -ABC (如图所示)， 其中底面ABC 是直角三角形，AB ⊥BC ，P A ⊥平面ABC ， BC ＝27，P A 2＋y 2＝102，(27)2＋P A 2＝x 2，因此xy ＝x 102－[x 2－（27）2]＝x128－x 2≤x 2＋（128－x 2）2＝64，当且仅当x 2＝128－x 2，即x ＝8时取等号，因此xy 的最大值是64，故选C.6．(2021·山西省第三次四校联考)在半径为10的球面上有A ，B ，C 三点，假如AB ＝83，∠ACB ＝60°，则球心O 到平面ABC 的距离为( )A ．2B ．4C ．6D ．8解析：选C.设A ，B ，C 三点所在圆的半径为r ，圆心为P .由于∠ACB ＝60°，所以∠APB ＝120°.在等腰三角形ABP 中，AP ＝43sin 60°＝8，所以r ＝8，所以球心O 到平面ABC 的距离为102－82＝6，故选C.7．如图是一个几何体的三视图，则该几何体的表面积是( )A ．5＋ 3B ．5＋2 3C ．4＋2 2D ．4＋2 3解析：选A.该几何体的直观图如图．表面积S ＝1×1＋12×1×1×2＋2×12×(1＋2)×1＋12×6×2＝5＋3，所以选A.8．在三棱锥P -ABC 中，P A ⊥平面ABC ，AC ⊥BC ，D 为侧棱PC 上的一点，它的正视图和侧视图如图所示，则下列命题正确的是( )A ．AD ⊥平面PBC ，且三棱锥D -ABC 的体积为83B ．BD ⊥平面P AC ，且三棱锥D -ABC 的体积为83C ．AD ⊥平面PBC ，且三棱锥D -ABC 的体积为163D ．BD ⊥平面P AC ，且三棱锥D -ABC 的体积为163解析：选C.由正视图可知，P A ＝AC ，且点D 为线段PC 的中点，所以AD ⊥PC .由侧视图可知，BC ＝4.由于P A ⊥平面ABC ，所以P A ⊥BC .又由于BC ⊥AC ，且AC ∩P A ＝A ，所以BC ⊥平面P AC ，所以BC ⊥AD .又由于AD ⊥PC ，且PC ∩BC ＝C ，所以可得AD ⊥平面PBC ，V D ­ABC ＝13×12×P A ×S △ABC ＝163.9．某几何体的正视图与俯视图如图所示，若俯视图中的多边形为正六边形，则该几何体的侧视图的面积为________．解析：侧视图由一个矩形和一个等腰三角形构成，矩形的长为3，宽为2，面积为3×2＝6.等腰三角形的底边为3，高为3，其面积为12×3×3＝32，所以侧视图的面积为6＋32＝152.答案：15210．(2021·洛阳市高三班级统考)如图是某几何体的三视图，则该几何体的外接球的表面积为( )解析：由三视图知，该几何体可以由一个长方体截去一个角后得到，该长方体的长、宽、高分别为5、4、3，所以其外接球半径R 满足2R ＝42＋32＋52＝52，所以该几何体的外接球的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎫5222＝50π.答案：50π 11．(2021·绍兴市高三诊断性测试)若某几何体的三视图如图所示，则该几何体的体积为________，最长的侧棱长为________．解析：依据三视图及有关数据还原该几何体，得该几何体是底面为直角梯形的四棱锥P -ABCD ，如图，过点P 作PH ⊥AD 于点H ，连接CH .底面面积S 1＝（1＋2）×12＝32，V ＝13×32×1＝12，最长的侧棱长为PB ＝ 3.答案：12312．设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2，若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________． 解析：设两个圆柱的底面半径和高分别为r 1，r 2和h 1，h 2，由S 1S 2＝94，得πr 21πr 22＝94，则r 1r 2＝32.由圆柱的侧面积相等，得2πr 1h 1＝2πr 2h 2，即r 1h 1＝r 2h 2，则h 1h 2＝23，所以V 1V 2＝πr 21h 1πr 22h 2＝32.答案：3213．(2021·洛阳市统考)已知点A ，B ，C ，D 均在球O 上，AB ＝BC ＝6，AC ＝23，若三棱锥D -ABC 体积的最大值为3，则球O 的表面积为________．解析：由题意可得，∠ABC ＝π2，△ABC 的外接圆半径r ＝3，当三棱锥的体积最大时，V D ­ABC ＝13S △ABC ·h (h为D 到底面ABC 的距离)，即3＝13×12×6×6h ⇒h ＝3，即R ＋R 2－r 2＝3(R 为外接球半径)，解得R ＝2，所以球O 的表面积为4π×22＝16π.答案：16π 14．(2021·杭州市联谊学校高三其次次联考)一个等腰直角三角形的三个顶点分别在正三棱柱ABC -A 1B 1C 1的三条侧棱上，已知正三棱柱的底面边长为2，则该三角形的斜边长为________．解析：如图，在正三棱柱ABC -A 1B 1C 1中，△ABC 为正三角形，边长为2，△DEF 为等腰直角三角形，DF 为斜边，设DF 的长为x ，则DE ＝EF ＝22x ，作DG ⊥BB 1，GH ⊥CC 1，EI ⊥CC 1，垂足分别为G ，H ，I ，则EG ＝DE 2－DG 2＝x 22－4，FI ＝EF 2－EI 2＝x 22－4，FH ＝FI ＋HI ＝FI ＋EG＝2x 22－4.连接DH ，在Rt △DHF 中，DF 2＝DH 2＋FH 2，即x 2＝4＋⎝⎛⎭⎫2x 22－42，解得x ＝23，即该三角形的斜边长为2 3.答案：2 3 15．(2021·浙江省名校新高考联盟第一次联考)如图，ABEDFC 为多面体，平面ABED 与平面ACFD 垂直，点O 在线段AD 上，OA ＝1，OD ＝2，△OAB ，△OAC ，△ODE ，△ODF 都是正三角形，则BC ＝________，四棱锥F-OBED的体积为________．解析：取AO的中点M，连接CM，BM，由△OAB，△OAC是正三角形，OA＝1，可知CM⊥AO，BM⊥AO，且BM＝CM＝32，又平面ABED⊥平面ACFD，所以CM⊥平面ABED，所以CM⊥BM，故BC＝62.过点F作FQ⊥OD于点Q，由于平面ABED⊥平面ACFD，所以FQ⊥平面ABED，FQ就是四棱锥F-OBED的高．易知FQ＝3，又S△OBE＝12×1×2×32＝32，S△OED＝12×2×2×32＝3，所以S四边形OBED＝32＋3＝332，故V四棱锥F-OBED＝13×332×3＝32.答案：6232。

选修4－4 坐标系与参数方程1．极坐标系(1)极坐标系的建立：在平面上取一个定点O ，叫做________，从O 点引一条射线Ox ，叫做________，再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就确定了一个极坐标系．设M 是平面内一点，极点O 与点M 的距离OM 叫做点M 的________，记为ρ，以极轴Ox 为始边，射线OM 为终边的角叫做点M 的极角，记为θ.有序数对(ρ，θ)叫做点M 的极坐标，记作M (ρ，θ)．(2)极坐标与直角坐标的关系：把直角坐标系的原点作为极点，x 轴的正半轴作为极轴，并在两种坐标系中取相同的长度单位，设M 是平面内任意一点，它的直角坐标是(x ，y )，极坐标为(ρ，θ)，则它们之间的关系为x ＝______，y ＝________.另一种关系为ρ2＝________，tan θ＝________. 2．简单曲线的极坐标方程 (1)直线的极坐标方程θ＝α (ρ∈R )表示过极点且与极轴成α角的直线； ρcos θ＝a 表示过(a,0)且垂直于极轴的直线； ρsin θ＝b 表示过⎝⎛⎭⎫b ，π2且平行于极轴的直线； ρsin(α－θ)＝ρ1sin(α－θ1)表示过(ρ1，θ1)且与极轴成α角的直线方程． (2)圆的极坐标方程ρ＝2r cos θ表示圆心在(r,0)，半径为|r |的圆； ρ＝2r sin θ表示圆心在⎝⎛⎭⎫r ，π2，半径为|r |的圆； ρ＝r 表示圆心在极点，半径为|r |的圆． 3．曲线的参数方程在平面直角坐标系xOy 中，如果曲线上任意一点的坐标x ，y 都是某个变量t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t ).并且对于t 的每一个允许值上式所确定的点M (x ，y )都在这条曲线上，则称上式为该曲线的________________，其中变量t 称为________．4．一些常见曲线的参数方程(1)过点P 0(x 0，y 0)，且倾斜角为α的直线的参数方程为________________(t 为参数)． (2)圆的方程(x －a )2＋(y －b )2＝r 2的参数方程为________________________(θ为参数)． (3)椭圆方程x 2a 2＋y 2b 2＝1(a >b >0)的参数方程为________________(θ为参数)．(4)抛物线方程y 2＝2px (p >0)的参数方程为________________(t 为参数)．1．在极坐标系中，直线ρsin(θ＋π4)＝2被圆ρ＝4截得的弦长为________．2．极坐标方程ρ＝sin θ＋2cos θ能表示的曲线的直角坐标方程为____________________．3．已知点P (3，m )在以点F 为焦点的抛物线⎩⎪⎨⎪⎧x ＝4t 2，y ＝4t (t 为参数)上，则PF ＝________.4．直线⎩⎪⎨⎪⎧x ＝－1＋t sin 40°，y ＝3＋t cos 40°(t 为参数)的倾斜角为________． 5．已知曲线C 的参数方程是⎩⎪⎨⎪⎧x ＝3t ，y ＝2t 2＋1(t 为参数)．则点M 1(0,1)，M 2(5,4)在曲线C 上的是________．题型一 极坐标与直角坐标的互化例1 在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系．曲线C 的极坐标方程为ρcos(θ－π3)＝1，M ，N 分别为C 与x 轴、y 轴的交点． (1)写出C 的直角坐标方程，并求M 、N 的极坐标；(2)设MN 的中点为P ，求直线OP 的极坐标方程．思维升华 直角坐标方程化为极坐标方程，只需把公式x ＝ρcos θ及y ＝ρsin θ直接代入并化简即可；而极坐标方程化为直角坐标方程要通过变形，构造形如ρcos θ，ρsin θ，ρ2的形式，进行整体代换．其中方程的两边同乘以(或同除以)ρ及方程两边平方是常用的变形方法．但对方程进行变形时，方程必须保持同解，因此应注意对变形过程的检验．在极坐标系中，已知圆ρ＝2cos θ与直线3ρcos θ＋4ρsin θ＋a ＝0相切，求实数a 的值．题型二 参数方程与普通方程的互化例2 已知两曲线参数方程分别为⎩⎨⎧x ＝5cos θ，y ＝sin θ(0≤θ<π)和⎩⎪⎨⎪⎧x ＝54t 2，y ＝t(t ∈R )，求它们的交点坐标．思维升华 (1)参数方程化为普通方程常用的消参技巧有代入消元、加减消元、平方后再加减消元等．对于与角θ有关的参数方程，经常用到的公式有sin 2θ＋cos 2θ＝1,1＋tan 2θ＝1cos 2θ等．(2)在将曲线的参数方程化为普通方程时，还要注意其中的x ，y 的取值范围，即在消去参数的过程中一定要注意普通方程与参数方程的等价性．将下列参数方程化为普通方程．(1)⎩⎪⎨⎪⎧x ＝2t 21＋t 2，y ＝4－2t21＋t2(t 为参数)；(2)⎩⎪⎨⎪⎧x ＝2－4cos 2θ，y ＝－1＋sin 2θ(θ为参数)．题型三 极坐标、参数方程的综合应用例3 在直角坐标平面内，以坐标原点O 为极点，x 轴的正半轴为极轴，建立极坐标系．曲线C 的极坐标方程是ρ＝4cos θ，直线l 的参数方程是⎩⎨⎧x ＝－3＋32t ，y ＝12t(t 为参数)，M ，N 分别为曲线C 、直线l 上的动点，求MN 的最小值．思维升华 涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．转化后可使问题变得更加直观，它体现了化归思想的具体运用．(2013·辽宁)在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系．圆C 1，直线C 2的极坐标方程分别为ρ＝4sin θ，ρcos ⎝⎛⎭⎫θ－π4＝2 2. (1)求C 1与C 2交点的极坐标；(2)设P 为C 1的圆心，Q 为C 1与C 2交点连线的中点．已知直线PQ 的参数方程为⎩⎪⎨⎪⎧x ＝t 3＋a ，y ＝b 2t 3＋1(t ∈R 为参数)，求a ，b 的值．参数的几何意义不明致误典例：(10分)已知直线l 的参数方程为⎩⎨⎧x ＝12t ，y ＝22＋32t(t 为参数)，若以直角坐标系xOy 的O 点为极点，Ox 方向为极轴，选择相同的长度单位建立极坐标系，得曲线C 的极坐标方程为ρ＝2cos(θ－π4)．(1)求直线l 的倾斜角；(2)若直线l 与曲线C 交于A ，B 两点，求AB .易错分析 不明确直线的参数方程中的几何意义导致错误． 规范解答解 (1)直线的参数方程可以化为⎩⎪⎨⎪⎧x ＝t cos 60°，y ＝22＋t sin 60°，[2分]根据直线参数方程的意义，直线l 经过点(0，22)， 倾斜角为60°.[4分](2)直线l 的直角坐标方程为y ＝3x ＋22，[6分] ρ＝2cos(θ－π4)的直角坐标方程为(x －22)2＋(y －22)2＝1，[8分]所以圆心(22，22)到直线l 的距离d ＝64. 所以AB ＝102.[10分] 温馨提醒 对于直线的参数方程⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)来说，要注意t 是参数，而α则是直线的倾斜角．与此类似，椭圆参数方程⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ的参数φ有特别的几何意义，它表示离心角．方法与技巧1．曲线的极坐标方程与直角坐标系的互化思路：对于简单的我们可以直接代入公式ρcos θ＝x ，ρsin θ＝y ，ρ2＝x 2＋y 2，但有时需要作适当的变化，如将式子的两边同时平方，两边同时乘以ρ等．2．参数方程化普通方程常用的消参技巧：代入消元、加减消元、平方后加减消元等，经常用到公式：cos 2θ＋sin 2θ＝1,1＋tan 2θ＝1cos 2θ.3．利用曲线的参数方程来求解两曲线间的最值问题非常简捷方便，是我们解决这类问题的好方法． 失误与防范1．极径ρ是一个距离，所以ρ≥0，但有时ρ可以小于零．极角θ规定逆时针方向为正，极坐标与平面直角坐标不同，极坐标与P 点之间不是一一对应的，所以我们又规定ρ≥0,0≤θ<2π，来使平面上的点与它的极坐标之间是一一对应的，但仍然不包括极点．2．在将曲线的参数方程化为普通方程时，还要注意其中的x ，y 的取值范围，即在消去参数的过程中一定要注意普通方程与参数方程的等价性．A 组 专项基础训练1．(2013·江苏)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t ＋1，y ＝2t (t 为参数)，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2tan 2θ，y ＝2tan θ(θ为参数)．试求直线l 和曲线C 的普通方程，并求出它们的公共点的坐标．2．已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝sin α，y ＝cos 2α，α∈[0,2π)，曲线D 的极坐标方程为ρsin(θ＋π4)＝－ 2.(1)将曲线C 的参数方程化为普通方程； (2)曲线C 与曲线D 有无公共点？试说明理由．3．(2013·福建)在平面直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系，已知点A 的极坐标为(2，π4)，直线l 的极坐标方程为ρcos(θ－π4)＝a ，且点A 在直线l 上．(1)求a 的值及直线l 的直角坐标方程；(2)圆C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，试判断直线l 与圆C 的位置关系．4．在极坐标系中，P 是曲线ρ＝12sin θ上的动点，Q 是曲线ρ＝12cos ⎝⎛⎭⎫θ－π6上的动点，试求PQ 的最大值．5．在极坐标系中，已知三点M ⎝⎛⎭⎫2，－π3、N (2,0)、P ⎝⎛⎭⎫23，π6. (1)将M 、N 、P 三点的极坐标化为直角坐标； (2)判断M 、N 、P 三点是否在一条直线上．6．在同一平面直角坐标系中，经过伸缩变换⎩⎨⎧x ′＝12x ，y ′＝13y后，曲线C ：x 2＋y 2＝36变为何种曲线，并求曲线的焦点坐标．B 组 专项能力提升1．在极坐标系中，已知圆O ：ρ＝cos θ＋sin θ和直线l ：ρsin(θ－π4)＝22.(1)求圆O 和直线l 的直角坐标方程；(2)当θ∈(0，π)时，求直线l 与圆O 公共点的极坐标．2．已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρcos(θ－π4)＝2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程； (2)求经过两圆交点的直线的极坐标方程．3．(2013·课标全国Ⅰ)已知曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝4＋5cos t ，y ＝5＋5sin t (t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝2sin θ. (1)把C 1的参数方程化为极坐标方程； (2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π)．4．(2012·辽宁)在直角坐标系xOy中，圆C1：x2＋y2＝4，圆C2：(x－2)2＋y2＝4.(1)在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆C1，C2的极坐标方程，并求出圆C1，C2的交点坐标(用极坐标表示)；(2)求圆C1与C2的公共弦的参数方程．答案要点梳理1．(1)极点 极轴 极径(2)ρcos θ ρsin θ x 2＋y 2 y x3．参数方程 参数4．(1)⎩⎪⎨⎪⎧ x ＝x 0＋t cos αy ＝y 0＋t sin α (2)⎩⎪⎨⎪⎧ x ＝a ＋r cos θy ＝b ＋r sin θ (3)⎩⎪⎨⎪⎧ x ＝a cos θy ＝b sin θ (4)⎩⎪⎨⎪⎧ x ＝2pt 2y ＝2pt 夯基释疑1．43 2.x 2＋y 2－2x －y ＝0 3.4 4.50° 5.M 1 题型分类·深度剖析例1 解 (1)由ρcos(θ－π3)＝1 得ρ(12cos θ＋32sin θ)＝1. 从而C 的直角坐标方程为12x ＋32y ＝1，即x ＋3y ＝2. 当θ＝0时，ρ＝2，所以M (2,0)．当θ＝π2时，ρ＝233，所以N (233，π2)． (2)M 点的直角坐标为(2,0)．N 点的直角坐标为(0，233)． 所以P 点的直角坐标为(1，33)． 则P 点的极坐标为(233，π6)， 所以直线OP 的极坐标方程为θ＝π6(ρ∈R )． 跟踪训练1 解 将极坐标方程化为直角坐标方程，得圆的方程为x 2＋y 2＝2x ，即(x －1)2＋y 2＝1，直线的方程为3x ＋4y ＋a ＝0.由题设知，圆心(1,0)到直线的距离为1，即有|3×1＋4×0＋a |32＋42＝1，解得a ＝－8或a ＝2. 故a 的值为－8或2.例2 解 将两曲线的参数方程化为普通方程分别为x 25＋y 2＝1 (0≤y ≤1，－5<x ≤5)和y 2＝45x ，联立解得交点为⎝⎛⎭⎫1，255. 跟踪训练2 解 (1)∵x ＝2t 21＋t2， ∴y ＝4－2t 21＋t 2＝4(1＋t 2)－6t 21＋t 2＝4－3×2t 21＋t 2＝4－3x . 又x ＝2t 21＋t 2＝2(1＋t 2)－21＋t 2＝2－21＋t 2∈[0,2)． ∴x ∈[0,2)．∴所求的普通方程为3x ＋y －4＝0(x ∈[0,2))．(2)∵4cos 2θ＝2－x,4sin 2θ＝4(y ＋1)．∴4cos 2θ＋4sin 2θ＝2－x ＋4y ＋4.∴4y －x ＋2＝0.∵0≤4cos 2θ≤4，∴0≤2－x ≤4，∴－2≤x ≤2.∴所求的普通方程为x －4y －2＝0(x ∈[－2,2])．例3 解 化极坐标方程ρ＝4cos θ为直角坐标方程x 2＋y 2－4x ＝0，所以曲线C 是以(2,0)为圆心，2为半径的圆．化参数方程⎩⎨⎧ x ＝－3＋32t ，y ＝12t(t 为参数)为普通方程x －3y ＋3＝0. 圆心到直线l 的距离d ＝|2＋3|1＋3＝52， 此时，直线与圆相离， 所以MN 的最小值为52－2＝12.跟踪训练3 解 (1)圆C 1的直角坐标方程为x 2＋(y －2)2＝4，直线C 2的直角坐标方程为x ＋y －4＝0.解⎩⎪⎨⎪⎧ x 2＋(y －2)2＝4，x ＋y －4＝0，得⎩⎪⎨⎪⎧ x 1＝0，y 1＝4，⎩⎪⎨⎪⎧ x 2＝2，y 2＝2.所以C 1与C 2交点的极坐标为⎝⎛⎭⎫4，π2，⎝⎛⎭⎫22，π4， 注：极坐标系下点的表示不唯一．(2)由(1)可得，P 点与Q 点的直角坐标分别为(0,2)，(1,3)．故直线PQ 的直角坐标方程为x －y ＋2＝0，由参数方程可得y ＝b 2x －ab 2＋1， 所以⎩⎨⎧ b 2＝1，－ab 2＋1＝2，解得a ＝－1，b ＝2.练出高分A 组 1．解 因为直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t ＋1，y ＝2t(t 为参数)， 由x ＝t ＋1得t ＝x －1，代入y ＝2t ，得到直线l 的普通方程为2x －y －2＝0.同理得到曲线C 的普通方程为y 2＝2x . 联立方程组⎩⎪⎨⎪⎧y ＝2(x －1)，y 2＝2x ， 解得公共点的坐标为(2,2)，⎝⎛⎭⎫12，－1. 2．解 (1)由⎩⎪⎨⎪⎧x ＝sin α，y ＝cos 2α，α∈[0,2π)得 x 2＋y ＝1，x ∈[－1,1]．(2)由ρsin(θ＋π4)＝－2得曲线D 的普通方程为 x ＋y ＋2＝0.⎩⎪⎨⎪⎧x ＋y ＋2＝0，x 2＋y ＝1得x 2－x －3＝0. 解得x ＝1±132∉[－1,1]， 故曲线C 与曲线D 无公共点．3．解 (1)由点A (2，π4)在直线ρcos(θ－π4)＝a 上，可得a ＝ 2. 所以直线l 的方程可化为ρcos θ＋ρsin θ＝2，从而直线l 的直角坐标方程为x ＋y －2＝0.(2)由已知得圆C 的直角坐标方程为(x －1)2＋y 2＝1，所以圆C 的圆心为(1,0)，半径r ＝1，因为圆心C 到直线l 的距离d ＝12＝22<1， 所以直线l 与圆C 相交．4．解 ∵ρ＝12sin θ，∴ρ2＝12ρsin θ，∴x 2＋y 2－12y ＝0，即x 2＋(y －6)2＝36.又∵ρ＝12cos ⎝⎛⎭⎫θ－π6， ∴ρ2＝12ρ⎝⎛⎭⎫cos θcos π6＋sin θsin π6， ∴x 2＋y 2－63x －6y ＝0， ∴(x －33)2＋(y －3)2＝36，∴PQ max ＝6＋6＋(33)2＋32＝18. 5．解 (1)由公式⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得M 的直角坐标为(1，－3)； N 的直角坐标为(2,0)；P 的直角坐标为(3，3)．(2)∵k MN ＝32－1＝3，k NP ＝3－03－2＝ 3. ∴k MN ＝k NP ，∴M 、N 、P 三点在一条直线上．6．解 圆x 2＋y 2＝36上任一点为P (x ，y )，伸缩变换后对应的点的坐标为P ′(x ′，y ′)，则⎩⎪⎨⎪⎧x ＝2x ′，y ＝3y ′， ∴4x ′2＋9y ′2＝36，即x ′29＋y ′24＝1. ∴曲线C 在伸缩变换后得椭圆x 29＋y 24＝1，其焦点坐标为(±5，0)． B 组1．解 (1)圆O ：ρ＝cos θ＋sin θ，即ρ2＝ρcos θ＋ρsin θ，圆O 的直角坐标方程为x 2＋y 2＝x ＋y ，即x 2＋y 2－x －y ＝0，直线l ：ρsin(θ－π4)＝22，即ρsin θ－ρcos θ＝1， 则直线l 的直角坐标方程为y －x ＝1，即x －y ＋1＝0.(2)由⎩⎪⎨⎪⎧ x 2＋y 2－x －y ＝0，x －y ＋1＝0得⎩⎪⎨⎪⎧x ＝0，y ＝1， 故直线l 与圆O 公共点的极坐标为(1，π2)． 2．解 (1)由ρ＝2知ρ2＝4，所以x 2＋y 2＝4；因为ρ2－22ρcos(θ－π4)＝2， 所以ρ2－22ρ(cos θcos π4＋sin θsin π4)＝2， 所以x 2＋y 2－2x －2y －2＝0.(2)将两圆的直角坐标方程相减，得经过两圆交点的直线方程为x ＋y ＝1.化为极坐标方程为ρcos θ＋ρsin θ＝1，即ρsin(θ＋π4)＝22. 3．解 (1)∵C 1的参数方程为⎩⎪⎨⎪⎧x ＝4＋5cos ty ＝5＋5sin t .∴⎩⎪⎨⎪⎧ 5cos t ＝x －45sin t ＝y －5. ∴(x －4)2＋(y －5)2＝25(cos 2t ＋sin 2t )＝25，即C 1的直角坐标方程为(x －4)2＋(y －5)2＝25，把x ＝ρcos θ，y ＝ρsin θ代入(x －4)2＋(y －5)2＝25，化简得：ρ2－8ρcos θ－10ρsin θ＋16＝0.(2)C 2的直角坐标方程为x 2＋y 2＝2y ，解方程组⎩⎪⎨⎪⎧(x －4)2＋(y －5)2＝25x 2＋y 2＝2y 得⎩⎪⎨⎪⎧ x ＝1y ＝1或⎩⎪⎨⎪⎧x ＝0y ＝2. ∴C 1与C 2交点的直角坐标为(1,1)，(0,2)．∴C 1与C 2交点的极坐标为⎝⎛⎭⎫2，π4，⎝⎛⎭⎫2，π2. 4．解 (1)圆C 1的极坐标方程为ρ＝2，圆C 2的极坐标方程为ρ＝4cos θ. 解⎩⎪⎨⎪⎧ρ＝2，ρ＝4cos θ得ρ＝2，θ＝±π3， 故圆C 1与圆C 2交点的坐标为⎝⎛⎭⎫2，π3，⎝⎛⎭⎫2，－π3. 注：极坐标系下点的表示不唯一． (2)方法一 由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ 得圆C 1与C 2交点的直角坐标分别为(1，3)，(1，－3)． 故圆C 1与C 2的公共弦的参数方程为⎩⎪⎨⎪⎧ x ＝1，y ＝t ，－3≤t ≤ 3. ⎝ ⎛⎭⎪⎪⎫或参数方程写成⎩⎪⎨⎪⎧x ＝1，y ＝y ，－3≤y ≤3方法二 将x ＝1代入⎩⎪⎨⎪⎧ x ＝ρcos θ，y ＝ρsin θ 得ρcos θ＝1，从而ρ＝1cos θ.于是圆C 1与C 2的公共弦的参数方程为⎩⎪⎨⎪⎧x ＝1，y ＝tan θ，－π3 ≤θ≤π3.。

文科物理会考复习学案（4）平抛运动、匀速圆周运动、万有引力定律编稿教师：李志强1. 能将平抛运动分解为水平和竖直方向的分运动，并能写出水平方向、竖直方向的分速度、分位移的表达式。

2. 知道匀速圆周运动的加速度、线速度之间的关系。

3. 记住匀速圆周运动的向心加速度、向心力的表达式，并能解决基本的匀速圆周运动动力学问题。

4. 记住万有引力定律的表达式，知道其适用范围。

水平: tvx=，vvx=竖直：221gty=，gtvy=2. 匀速圆周运动各个物理量之间的关系：v rω=，22rTvππω==,3. 匀速圆周运动的向心加速度：22224va r rr Tπω===向心力：22224vF m r m m rr Tπω===4. 万有引力定律：122m mF Gr=5. 质量为m的卫星绕质量为M的星球做匀速圆周运动，万有引力提供向心力：222224Mm vG m m r m rr r Tπω===【例1】以10m/s的速度从10m高的塔上水平抛出一个石子。

不计空气阻力，取g=10m/s2，石子落地时的速度大小是（）A. B.C. 20m/sD. 30m/s【例2】如图所示，在探究平抛运动规律的实验中，用小锤打击弹性金属片，金属片把P球沿水平方向抛出，同时Q球被松开而自由下落，P、Q两球同时开始运动.此后，可以观察到小球P与小球Q （选填“同时”或“不同时”）落到水平地面上；若小球Q在空中运动的时间为t，小球P、Q落地点间的距离为x，在小球P被弹出时的水平初速度为。

【练习】从同一高度以不同的初速度水平抛出两个小球，小球都做平抛运动，最后落到同一水平地面上，两个小球在空中运动的时间（选填“相等”或“不相等”），落地时的速度（选填“相同”或“不相同”）。

【例3】若将平抛运动沿水平和竖直两个方向进行分解，则下列说法中正确的是（）A. 水平方向的分运动是匀速直线运动B. 水平方向的分运动是匀加速直线运动C. 竖直方向的分运动是匀速直线运动D. 竖直方向的分运动是自由落体运动【例4】物体在做匀速圆周运动的过程中，下列物理量中变化的是（）A. 周期B. 动能C. 线速度D. 角速度【例5】两个质量为m1、m2的质点相距为r时，它们之间的万有引力大小为F，若将它们的距离增大为2r，则它们之间的万有引力大小为（）A. 2FB. F/2C. 4FD. F/4【例6】质量相同的人造卫星，如果在不同轨道上绕地球做匀速圆周运动，那么，下列判断中正确的是（）A. 轨道半径大的卫星所受向心力大B. 轨道半径大的卫星所受向心力小C. 轨道半径大的卫星运行速度大D. 轨道半径大的卫星运行速度小【例7】在如图所示的皮带传动装置中，A是大轮边缘上的一点，B是小轮边缘上的一点。