江苏省常州市武进区八年级数学上册第一章全等三角形练习七新版苏科版【word版】.doc

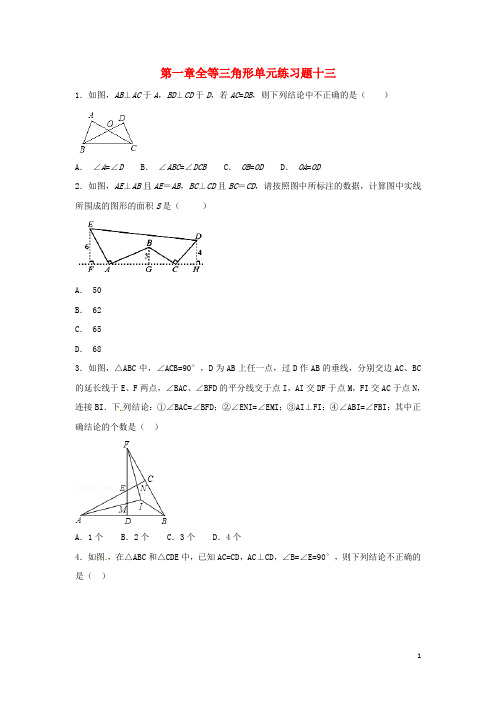
第一章全等三角形单元练习题十三1．如图，AB⊥AC于A，BD⊥CD于D，若AC=DB，则下列结论中不正确的是（）A．∠A=∠D B．∠ABC=∠DCB C．OB=OD D．OA=OD2．如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）A． 50B． 62C． 65D． 683．如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC 的延长线于E、F两点，∠BAC、∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI．下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（）A．1个 B．2个 C．3个 D．4个4．如图，在△ABC和△CDE中，已知AC=CD，AC⊥CD，∠B=∠E=90°，则下列结论不正确的是（）A．∠A与∠D互为余角B．∠A=∠2C．△ABC≌△CEDD．∠1=∠25．如图，已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD、BC于点E、F，则下列结论：①OA=OC ②OE=OF ③AE=CF ④OB=OD，其中成立的个数是（）A、1 B、2 C、3 D、46．下列命题中，是真命题的是（）A、一个角的补角大于这个角B、面积相等的两个三角形全等C、三角形的三条高线相交于三角形内一点D、成轴对称的两个图形是全等图形7．在△ABC中，∠ABC＝30°，AB边长为10，AC边的长度可以在3、5、7、9、11中取值，满足这些条件的互不全等的三角形的个数是（）A．3个 B．4个 C．5个 D．6个8．判断下列各命题（1）若a＞b，则a2＞b2；（2）两条直线被第三条直线所截，同位角相等；（3）在同一平面内，经过一点有且只有一条直线垂直于已知直线．（4）三个角对应相等的两个三角形全等；其中假命题是（）A．（1）（2）（3） B．（1）（2）（4） C．（2）（3）（4） D．（1）（3）（4）9．根据下列条件，能判定△ABC≌△A′B′C′的是（）A、AB=A′B′，BC=B′C′，∠A=∠A′B、∠A=∠A′，∠B=∠B′，AC=B′C′C、∠A=∠A′，∠B=∠B′，∠C=∠C′D、AB=A′B′，BC=B′C′，△ABC与△A′B′C′的周长相等10．如图，在△ABC和△DCB中，∠A=∠D=90°，AB=CD，∠ACB=30°，则∠ACD的度数为（）A．10° B．2° C．30° D．40°11．如图，若△OAC≌△OBD，且∠O=65°，∠C=20°，则∠OBD= ．12．如图，△ABC≌△ADE，则，AB=_____，∠E=∠_____．若∠BAE=120°，∠BAD=40°，则∠BAC=_____．13．如图，已知△ABD≌△ACE，∠1=75°，则∠2= °.14．如图，黄芳不小心把一块三角形的玻璃摔成三块碎片，现要带其中一块去配出与原来完全一样的玻璃，正确的办法是带第_________块去配，其依据是定理_________(写简称)15．（2015秋•南京期中）如图，在△ABC中，∠ACB=90°，∠CAB=30°．以AB长为一边作△ABD，且AD=BD，∠ADB=90°，取AB中点E，连DE、CE、CD．则∠EDC= °．16．如图，△ABC≌△DCB，AC与BD相交于点E，若∠A＝∠D＝80°，∠ABC＝60°，则∠BEC 等于________．17．如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E，F分别在AC，BC边上运动（点E不与点A，C重合），且保持ED⊥FD，连接DE，DF，EF，在此运动变化的过程中，有下列结论：①AE=CF；②EF最大值为22；③四边形CEDF的面积不随点E位置的改变而发生变化；④点C到线段EF的最大距离为2．其中结论正确的有（把所有正确答案的序号都填写在横线上）18．如图所示，在△ABC中，∠B=∠C=50°，BD=CF，BE=CD，则∠EDF的度数是_____.19．如图所示，在完全重合放置的两张矩形纸片ABCD中，AB=4，BC=8，将上面的矩形纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG，则图中阴影部分的面积为．20．阅读下面材料：小明遇到这样一个问题：如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．请回答：（1）在图2中，小明得到的全等三角形是△≌△；（2）BC和AC、AD之间的数量关系是．参考小明思考问题的方法，解决问题：如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9．求AB的长．21．如图，在四边形ABCD中，∠ABC=∠BCD=60°，AB+DC=BC．（1）如图1，连结AC 、BD ，求证：AC=BD ；（2）如图2，∠BAD 与∠ADC 的平分线相交于E 点，求∠E 的度数；（3）如图3，若AB=6，CD=3，点P 为BC 上一点，且∠APD=60°，试判断△APD 的形状，并说明理由．22．如图，点F ，G 分别在△ADE 的AD ，DE 边上，C ，B 依次为GF 延长线上两点，AB=AD ，∠B AF=∠CAE ，∠B=∠D ．（1）求证：BC=DE ；（2）若∠B=35°，∠AFB=78°，直接写出∠DGB 的度数．23．（1）如图1，ABC △和CDE △都是等边三角形，且D C B 、、三点共线，连接BE AD 、相交于点P ，求证：BE AD =．（2）如图2，在BCD △中，120<∠BCD °，分别以CD BC 、和BD 为边在BCD △外部作等边ABC △、等边CDE △和等边BDF △，联结BE AD 、和CF 交于点P ，下列结论中正确的是 （只填序号即可）①CF BE AD ==；②ADC BEC ∠=∠；③ 60=∠=∠=∠CPA EPC DPE °；（3）如图2，在（2）的条件下，求证：BE PD PC PB =++．24．如图，△ABE和△ACD有公共点A，∠BAC=∠DAE=90°，AB=AC，AE=AD，延长BE分别交AC、CD于点M、F．54321MFEDCBA求证：（1）△ABE≌△ACD．（2）BF⊥CD．25．如图，点C，D在线段BF上，AB∥DE，AB=DF，∠A=∠F．求证：BC=DE．26．如图，AB=AC，MB=MC．求证：直线AM垂直平分线段BC．27．如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：∠ADE=∠AED．。

苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)的全部内容。

第一章全等三角形单元测试一、单选题(共10题；共30分）1.如图,已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A、∠A=∠CB、AD=CBC、BE='DF'D、AD∥BC2。

如图，D在AB上，E在AC上,且∠B=∠C，那么补充下列条件后,不能判定△ABE≌△ACD的是（）A、AD=AEB、BE=CDC、∠AEB=∠ADCD、AB=AC3.如图所示，△ABD≌△CDB,下面四个结论中，不正确的是（）A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D。

AD∥BC,且AD=BC4。

如图，在下列条件中,不能证明△ABD≌△ACD的是（)A。

BD=DC，AB=AC B.∠ADB=∠ADC，BD=DCC.∠B=∠C,∠BAD=∠CADD.∠B=∠C，BD=DC5.已知图中的两个三角形全等，则∠1等于( ）A。

72° B。

60° C.50° D.58°6.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时,得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=12AC•BD,其中正确的结论有（）A.0个B.1个C.2个 D。

苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题，共计45分)1、如图，在平面直角坐标系中，一次函数的图象与x轴、y轴分别相交于点B，点A，以线段AB为边作正方形，且点C在反比例函数的图象上，则k的值为（）A.-12B.-42C.42D.-212、已知图中的两个三角形全等，则∠度数是（）A.72°B.60°C.58°D.50°3、如图所示，在∠AOB的两边截取AO=BO，CO=DO，连结AD、BC交于点P，考察下列结论:①△AOD≌△BOC ②△APC≌△BPD ③PC=PD.其中正确的是（）A.①②③B.只有①②C.只有②D.只有①4、如图，，，垂足分别为点，点，、相交于点O，，则图中全等三角形共有（）A.2对B.3对C.4对D.5对5、如图，在矩形ABCD中，AD= AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①△ABE ≌△ADH；②HE=CE；③H是BF的中点；④AB=HF；其中正确的有（）A.1个B.2个C.3个D.4个6、已知，如图△ABC中，AB＝5，AC＝3，则中线AD的取值范围是（）A.2＜AD＜8B.2＜AD＜4C.1＜AD＜4D.1＜AD＜87、已知，如图，为线段上一动点（不与点，重合），在同侧分别作等边三角形和等边三角形，与交于点，与交于点，与交于点，连结，，，以下四个结论：①；②三角形是等边三角形；③；④平分，其中正确的结论是（）A.①②B.③④C.①②③D.①②④8、如图是用尺规作一个角的角平分线的示意图，其根据是构造两个三角形全等．由作法知，能判定△MOC≌△NOC的依据是（）A.SASB.SSSC.ASAD.AAS9、如图，在△ABC中，∠ABC＝45°，AC＝5，H是高BD和CE的交点，则BH的长为（）A.3B.4C.5D.610、在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，则添加下列条件后不能判定两个三角形全等的是（）A.AC=A'C'B.BC=B'C'C.∠B=∠B'D.∠C=∠C'11、如图，已知AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE与CF交于点D，则下列结论中错误的是（）A.△ABE≌△ACFB.△BDF≌△CDEC.点D是BE的中点D.点D 在∠BAC的平分线上12、如图已知，AC=AD，BC=BD，便能知道∠ABC=∠ABD．这是根据什么理由得到的，小芳想了想，马上得出了正确的答案．你猜想小芳说的依据是（）A.SASB.SSAC.ASAD.SSS13、如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中一定和△ABC全等的是( )A.甲、乙B.甲、丙C.乙、丙D.乙14、如图，已知AB=AC ， BD=CD ，那么下列结论中不正确的是（）A. △ ABD ≌△ ACDB. ∠ ADB=90°C. ∠ BAD是∠ B的一半D. AD平分∠ BAC15、如图，△ABC的面积为9cm2， BP平分∠ABC，AP⊥BP于P，连接PC，则△PBC的面积为（）A.3cm 2B.4cm 2C.4.5cm 2D.5cm 2二、填空题(共10题，共计30分)16、如图，△ABC与△A'B'C'关于直线l对称，且∠A=105°，∠C'=30°，则∠B的度数为________17、如图，在菱形中，是的中点，连接，，将沿直线翻折，使得点落在上的点处，连接并延长交于点，则的值为________.18、一个三角形的三条边的长分别是3，5，7，另一个三角形的三条边的长分别是3，3x﹣2y，x+2y，若这两个三角形全等，则x+y的值是________．19、如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是________20、如图，已知∠ACD=∠BCE，AC=DC，如果要得到△ACB≌△DCE，那么还需要添加的条件是________．（填写一个即可，不得添加辅助线和字母）21、如图，△ABD≌△ACE，AD=8cm，AB=3cm，则BE=________cm22、如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2cm，BE＝0.5cm，则DE＝________cm.23、如图，已知，D是BC的中点，E是AD的中点，则AF：FC＝________.24、如图，在中，，，平分交于点，于点.若，则的周长为________cm.25、从同一张底片上冲出来的两张五寸照片________ 全等图形，从同一张底片上冲出来的一张一寸照片和一张两寸照片________ 全等图形（填“是”或“不是”）．三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、如图，点A，F，E，D在一条直线上，AB＝CD，AF＝DE，∠BAE＝∠CDF．求证：BE=CF．28、如图，点B，C分别在的两边上，点D是内一点，，，垂足分别为E，F，且，求证：．29、如图，在△ABC与△FDE中，点D在AB上，点B在DF上，∠C＝∠E，AC∥FE，AD＝FB.求证：△ABC≌△FDE.30、如图，已知：AB＝AC，BD＝CD，点P是AD延长线上的一点.求证：PB＝PC.参考答案一、单选题(共15题，共计45分)1、D2、D3、A5、C6、C7、D8、B9、C10、B11、C12、D13、C14、C15、C二、填空题(共10题，共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、29、。

一、八年级数学全等三角形解答题压轴题（难）1．如图，在ABC 中，45ABC ∠=,AD ,BE 分别为BC ,AC 边上的高，连接DE ,过点D 作DF DE ⊥与点F ，G 为BE 中点，连接AF ，DG ．（1）如图1，若点F 与点G 重合，求证：AF DF ⊥；（2）如图2，请写出AF 与DG 之间的关系并证明．【答案】(1)详见解析;(2)AF=2DG,且AF ⊥DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE ≌△DBF,从而得出△FDE 是等腰直角三角形,再证明△AEF 是等腰直角三角形,即可.(2) 延长DG 至点M,使GM=DG,交AF 于点H,连接BM, 先证明△BGM ≌△EGD,再证明△BDM ≌△DAF 即可推出.【详解】解:（1）证明:设BE 与AD 交于点H..如图，∵AD,BE 分别为BC,AC 边上的高,∴∠BEA=∠ADB=90°.∵∠ABC=45°,∴△ABD 是等腰直角三角形.∴AD=BD.∵∠AHE=∠BHD,∴∠DAC=∠DBH.∵∠ADB=∠FDE=90°,∴∠ADE=∠BDF.∴△DAE ≌△DBF.∴BF=AE,DF=DE.∴△FDE是等腰直角三角形.∴∠DFE=45°.∵G为BE中点,∴BF=EF.∴AE=EF.∴△AEF是等腰直角三角形.∴∠AFE=45°.∴∠AFD=90°,即AF⊥DF.（2）AF=2DG,且AF⊥DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,∵点G为BE的中点,BG=GE.∵∠BGM∠EGD,∴△BGM≌△EGD.∴∠MBE=∠FED=45°,BM=DE.∴∠MBE=∠EFD,BM=DF.∵∠DAC=∠DBE,∴∠MBD=∠MBE+∠DBE=45°+∠DBE.∵∠EFD=45°=∠DBE+∠BDF,∴∠BDF=45°-∠DBE.∵∠ADE=∠BDF,∴∠ADF=90°-∠BDF=45°+∠DBE=∠MBD.∵BD=AD,∴△BDM≌△DAF.∴DM=AF=2DG,∠FAD=∠BDM.∵∠BDM+∠MDA=90°,∴∠MDA+∠FAD=90°.∴∠AHD=90°.∴AF⊥DG.∴AF=2DG,且AF⊥DG【点睛】本题考查三角形全等的判定和性质,关键在于灵活运用性质.2．如图1，在平面直角坐标系中，点D（m，m+8）在第二象限，点B（0，n）在y轴正半轴上，作DA ⊥x 轴，垂足为A ，已知OA 比OB 的值大2，四边形AOBD 的面积为12．（1）求m 和n 的值．（2）如图2，C 为AO 的中点，DC 与AB 相交于点E ，AF ⊥BD ，垂足为F ，求证：AF ＝DE ．（3）如图3，点G 在射线AD 上，且GA ＝GB ，H 为GB 延长线上一点，作∠HAN 交y 轴于点N ，且∠HAN ＝∠HBO ，求NB ﹣HB 的值．【答案】（1）42m n =-⎧⎨=⎩（2）详见解析；（3）NB ﹣FB ＝4（是定值），即当点H 在GB 的延长线上运动时，NB ﹣HB 的值不会发生变化．【解析】【分析】（1）由点D ，点B 的坐标和四边形AOBD 的面积为12，可列方程组，解方程组即可； （2）由（1）可知，AD ＝OA ＝4，OB ＝2，并可求出AB ＝BD ＝25，利用SAS 可证△DAC ≌△AOB ，并可得∠AEC ＝90°，利用三角形面积公式即可求证；（3）取OC ＝OB ，连接AC ，根据对称性可得∠ABC ＝∠ACB ，AB ＝AC ，证明△ABH ≌△CAN ，即可得到结论.【详解】解：（1）由题意()()218122m n n m m --=⎧⎪⎨++-=⎪⎩ 解得42m n =-⎧⎨=⎩； （2）如图2中，由（1）可知，A （﹣4，0），B （0，2），D （﹣4，4），∴AD ＝OA ＝4，OB ＝2，∴由勾股定理可得：AB ＝BD ＝5∵AC ＝OC ＝2，∴AC＝OB，∵∠DAC＝∠AOB＝90°，AD＝OA，∴△DAC≌△AOB（SAS），∴∠ADC＝∠BAO，∵∠ADC+∠ACD＝90°，∴∠EAC+∠ACE＝90°，∴∠AEC＝90°，∵AF⊥BD，DE⊥AB，∴S△ADB＝12•AB•AE＝12•BD•AF，∵AB＝BD，∴DE＝AF．（3）解：如图，取OC＝OB，连接AC，根据对称性可得∠ABC＝∠ACB，AB＝AC，∵AG＝BG，∴∠GAB＝∠GBA，∵G为射线AD上的一点，∴AG∥y轴，∴∠GAB＝∠ABC，∴∠ACB＝∠EBA，∴180°﹣∠GBA＝180°﹣∠ACB，即∠ABG＝∠ACN，∵∠GAN＝∠GBO，∴∠AGB＝∠ANC，在△ABG与△ACN中，ABH ACNAHB ANCAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABH≌△ACN（AAS），∴BF＝CN，∴NB﹣HB＝NB﹣CN＝BC＝2OB，∵OB＝2∴NB﹣FB＝2×2＝4（是定值），即当点H在GB的延长线上运动时，NB﹣HB的值不会发生变化．【点睛】本题属于三角形综合题，全等三角形的判定和性质，解题的关键是相结合添加常用辅助线，构造图形解决问题，学会利用参数构建方程解决问题．3．(1)如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段EF，BE，FD之间的数量关系．小明同学探究的方法是：延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论是（直接写结论，不需证明）；(2)如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的二分之一，上述结论是否仍然成立，并说明理由．(3)如图3，四边形ABCD是边长为5的正方形，∠EBF=45°，直接写出三角形DEF的周长．【答案】（1）EF=BE+DF．（2）成立，理由见解析；（3）10.【解析】【分析】（1）如图1，延长FD到G，使得DG=DC,先证△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，进一步根据题意得∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.(2)如图2，延长FD到点G．使DG=BE．连结AG，证得△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，再结合题意得到∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.（3）如图3，延长DC到点G，截取CG=AE，连接BG，先证△AEB≌△CGB，得到BE=BG，∠ABE=∠CBG，结合已知条件得∴∠CBF+∠CBG=45°，再证明△EBF≌△GBF，得到EF=FG，最后求三角形的周长即可.【详解】解答：（1）解：如图1，延长FD到G，使得DG=DC在△ABE和△ADG中，∵DC DGB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；故答案为：EF=BE+DF．（2）解：结论EF=BE+DF仍然成立；理由：如图2，延长FD到点G．使DG=BE．连结AG在△ABE和△ADG中，∵DG BEB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAF AF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；（3）解：如图3，延长DC到点G，截取CG=AE，连接BG，在△AEB与△CGB中，∵AE CGA BOG AF BF=⎧⎪∠=∠⎨⎪=⎩，∴△AEB≌△CGB（SAS），∴BE=BG，∠ABE=∠CBG．∵∠EBF=45°，∠ABC=90°，∴∠ABE+∠CBF=45°，∴∠CBF+∠CBG=45°．在△EBF与△GBF中，∵BE BGEBF GBF BF BF=⎧⎪∠=∠⎨⎪=⎩，∴△EBF≌△GBF（SAS），∴EF=GF，∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10．【点睛】本题主要考查了三角形全等的判定和性质，灵活运用全等三角形的性质和判定是解答本题的关键.但本题分为三问，难度不断增加，对提升思维能力大有好处.4．如图1所示，已知点D 在AC 上，ADE ∆和ABC ∆都是等腰直角三角形，点M 为EC 的中点.（1）求证：BMD ∆为等腰直角三角形；（2）将ADE ∆绕点A 逆时针旋转45︒，如图2所示，（1）中的“BMD ∆为等腰直角三角形”是否仍然成立？请说明理由；（3）将ADE ∆绕点A 逆时针旋转一定的角度，如图3所示，（1）中的“BMD ∆为等腰直角三角形”成立吗？请说明理由.【答案】（1）详见解析；（2）是，证明详见解析；（3）成立，证明详见解析.【解析】【分析】()1根据等腰直角三角形的性质得出45ACB BAC ∠∠==，90ADE EBC EDC ∠∠∠===，推出BM DM =，BM CM =，DM CM =，推出BCM MBC ∠∠=，ACM MDC ∠∠=，求出22290BMD BCM ACM BCA ∠∠∠∠=+==即可． ()2延长ED 交AC 于F ，求出12DM FC =，//DM FC ，DEM NCM ∠=，根据ASA 推出EDM ≌CNM ，推出DM BM =即可．()3过点C 作//CF ED ，与DM 的延长线交于点F ，连接BF ，推出MDE ≌MFC ，求出DM FM =，DE FC =，作AN EC ⊥于点N ，证BCF ≌BAD ，推出BF BD =，DBA CBF ∠∠=，求出90DBF ∠=，即可得出答案．【详解】()1证明：ABC 和ADE 都是等腰直角三角形，45ACB BAC ∠∠∴==，90ADE EBC EDC ∠∠∠===点M 为EC 的中点，12BM EC ∴=，12DM EC =， BM DM ∴=，BM CM =，DM CM =，BCM MBC ∠∠∴=，DCM MDC ∠∠=，2BME BCM MBC BCE∠∠∠∠∴=+=，同理2DME ACM∠∠=，22224590 BMD BCM ACM BCA∠∠∠∠∴=+==⨯= BMD∴是等腰直角三角形．()2解：如图2，BDM是等腰直角三角形，理由是：延长ED交AC于F，ADE和ABC△是等腰直角三角形，45BAC EAD∠∠∴==，AD ED⊥，ED DF∴=，M为EC中点，EM MC∴=，12DM FC∴=，//DM FC，45BDN BND BAC∠∠∠∴===，ED AB⊥，BC AB⊥，//ED BC∴，DEM NCM∠∴=，在EDM和CNM中DEM NCMEM CMEMD CMN∠=∠⎧⎪=⎨⎪∠=∠⎩EDM∴≌()CNM ASA，DM MN∴=，BM DN∴⊥，BMD∴是等腰直角三角形．()3BDM是等腰直角三角形，理由是：过点C 作//CF ED ，与DM 的延长线交于点F ，连接BF ，可证得MDE ≌MFC ，DM FM ∴=，DE FC =，AD ED FC ∴==，作AN EC ⊥于点N ，由已知90ADE ∠=，90ABC ∠=，可证得DEN DAN ∠∠=，NAB BCM ∠∠=，//CF ED ，DEN FCM ∠∠∴=，BCF BCM FCM NAB DEN NAB DAN BAD ∠∠∠∠∠∠∠∠∴=+=+=+=， BCF ∴≌BAD ，BF BD ∴=，DBA CBF ∠∠=，90DBF DBA ABF CBF ABF ABC ∠∠∠∠∠∠∴=+=+==，DBF ∴是等腰直角三角形，点M 是DF 的中点，则BMD 是等腰直角三角形，【点睛】本题考查了等腰直角三角形的性质，全等三角形的性质和判定，直角三角形斜边上中线性质的应用，在本题中需要作辅助线来证明，难度较大．5．如图，AB=12cm ，AC ⊥AB ，BD ⊥AB ，AC=BD=9cm ，点P 在线段AB 上以3 cm/s 的速度，由A 向B 运动，同时点Q 在线段BD 上由B 向D 运动．（1）若点Q 的运动速度与点P 的运动速度相等，当运动时间t=1（s ），△ACP 与△BPQ 是否全等？说明理由，并直接判断此时线段PC 和线段PQ 的位置关系；（2）将 “AC ⊥AB ，BD ⊥AB ”改为“∠CAB=∠DBA ”，其他条件不变．若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能使△ACP 与△BPQ 全等. （3）在图2的基础上延长AC ，BD 交于点E ，使C ，D 分别是AE ，BE 中点，若点Q 以（2）中的运动速度从点B 出发，点P 以原来速度从点A 同时出发，都逆时针沿△ABE 三边运动，求出经过多长时间点P 与点Q 第一次相遇．【答案】（1）△ACP ≌△BPQ ，理由见解析；线段PC 与线段PQ 垂直（2）1或32（3）9s 【解析】【分析】（1）利用SAS 证得△ACP ≌△BPQ ，得出∠ACP=∠BPQ ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP ≌△BPQ ，分两种情况：①AC=BP ，AP=BQ ，②AC=BQ ，AP=BP ，建立方程组求得答案即可．（3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，据此列出方程，解这个方程即可求得．【详解】（1）当t=1时，AP=BQ=3，BP=AC=9，又∵∠A=∠B=90°，在△ACP 与△BPQ 中，AP BQ A B AC BP =⎧⎪∠=∠⎨⎪=⎩，∴△ACP ≌△BPQ （SAS ），∴∠ACP=∠BPQ ，∴∠APC+∠BPQ=∠APC+∠ACP=90°，∠CPQ=90°，则线段PC 与线段PQ 垂直.（2）设点Q 的运动速度x,①若△ACP ≌△BPQ ，则AC=BP ，AP=BQ ，912t t xt =-⎧⎨=⎩， 解得31t x =⎧⎨=⎩， ②若△ACP ≌△BPQ ，则AC=BQ ，AP=BP ，912xt t t =⎧⎨=-⎩解得632t x =⎧⎪⎨=⎪⎩， 综上所述，存在31t x =⎧⎨=⎩或632t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. （3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，设经过x 秒后P 与Q 第一次相遇，∵AC=BD=9cm ，C ，D 分别是AE ，BD 的中点；∴EB=EA=18cm.当V Q =1时，依题意得3x=x+2×9，解得x=9；当V Q=32时，依题意得3x=32x+2×9，解得x=12.故经过9秒或12秒时P与Q第一次相遇.【点睛】本题考查了一元一次方程的应用，解题的关键是熟练的掌握一元一次方程的性质与运算.6．已知△ABC中，AB=AC，点P是AB上一动点，点Q是AC的延长线上一动点，且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同，PQ与BC相交于点D，若AB=82，BC=16．（1）如图1，当点P为AB的中点时，求CD的长；（2）如图②，过点P作直线BC的垂线，垂足为E，当点P、Q在移动的过程中，设BE+CD=λ，λ是否为常数？若是请求出λ的值，若不是请说明理由．【答案】（1）4；（2）8【解析】【分析】（1）过P点作PF∥AC交BC于F，由点P和点Q同时出发，且速度相同，得出BP=CQ，根据PF∥AQ，可知∠PFB=∠ACB，∠DPF=∠CQD，则可得出∠B=∠PFB，证出BP=PF，得出PF=CQ，由AAS证明△PFD≌△QCD，得出，再证出F是BC的中点，即可得出结果；（2）过点P作PF∥AC交BC于F，易知△PBF为等腰三角形，可得BE=12BF，由（1）证明方法可得△PFD≌△QCD 则有CD=12CF，即可得出BE+CD=8．【详解】解:（1）如图①，过P点作PF∥AC交BC于F，∵点P 和点Q 同时出发，且速度相同，∴BP=CQ ，∵PF ∥AQ ，∴∠PFB=∠ACB ，∠DPF=∠CQD ，又∵AB=AC ，∴∠B=∠ACB ，∴∠B=∠PFB ，∴BP=PF ，∴PF=CQ ，又∠PDF=∠QDC ，∴△PFD ≌△QCD ，∴DF=CD=12CF ， 又因P 是AB 的中点，PF ∥AQ ， ∴F 是BC 的中点，即FC=12BC=8， ∴CD=12CF=4； （2）8BE CD λ+==为定值．如图②，点P 在线段AB 上，过点P 作PF ∥AC 交BC 于F ，易知△PBF 为等腰三角形，∵PE ⊥BF∴BE=12BF ∵易得△PFD ≌△QCD∴CD=12CF ∴()111182222BE CD BF CF BF CF BC λ+==+=+== 【点睛】 此题考查了等腰三角形的性质，全等三角形的判断与性质，熟悉相关性质定理是解题的关键．7．如图，Rt △ABC ≌Rt △CED （∠ACB ＝∠CDE ＝90°），点D 在BC 上，AB 与CE 相交于点F(1) 如图1，直接写出AB 与CE 的位置关系(2) 如图2，连接AD 交CE 于点G ，在BC 的延长线上截取CH ＝DB ，射线HG 交AB 于K ，求证：HK ＝BK【答案】（1）AB ⊥CE ；（2）见解析.【解析】【分析】（1）由全等可得∠ECD=∠A ，再由∠B+∠A=90°，可得∠B+ECD=90°，则AB ⊥CE. （2）延长HK 于DE 交于H ，易得△ACD 为等腰直角三角形，∠ADC=45°，易得DH=DE ，然后证明△DGH ≌△DGE ，所以∠H=∠E ，则∠H=∠B ，可得HK=BK.【详解】解：（1）∵Rt △ABC ≌Rt △CED ，∴∠ECD=∠A ，∠B=∠E ，BC=DE ，AC=CD∵∠B+∠A=90°∴∠B+ECD=90°∴∠BFC=90°，∴AB ⊥CE（2）在Rt △ACD 中，AC=CD ，∴∠ADC=45°，又∵∠CDE=90°，∴∠HDG=∠CDG=45°∵CH ＝DB ，∴CH+CD=DB+CD ，即HD=BC ，∴DH=DE ，在△DGH 和△DGE 中，DH=DEHDG=EDG=45DG=DG⎧⎪∠∠⎨⎪⎩∴△DGH≌△DGE（SAS）∴∠H=∠E又∵∠B=∠E∴∠H=∠B，∴HK=BK【点睛】本题考查全等三角形的判定与性质，利用全等找出角相等，再利用等角对等边判定线段相等是本题的关键.8．在ABC中，AB AC=，点D在BC边上，且60,ADB E∠=︒是射线DA上一动点(不与点D重合，且DA DB≠)，在射线DB上截取DF DE=，连接EF．()1当点E在线段AD上时，①若点E与点A重合时，请说明线段BF DC=；②如图2，若点E不与点A重合，请说明BF DC AE=+；()2当点E在线段DA的延长线上()DE DB>时，用等式表示线段,,AE BF CD之间的数量关系(直接写出结果，不需要证明)．【答案】（1）①证明见解析；②证明见解析；（2）BF＝AE-CD【解析】【分析】（1）①根据等边对等角，求到B C∠=∠，再由含有60°角的等腰三角形是等边三角形得到ADF∆是等边三角形，之后根据等边三角形的性质以及邻补角的性质得到120AFB ADC∠=∠=︒，推出ABF ACD∆∆≌，根据全等三角形的性质即可得出结论；②过点A做AG∥EF交BC于点G，由△DEF为等边三角形得到DA＝DG，再推出AE＝GF，根据线段的和差即可整理出结论；（2）根据题意画出图形，作出AG，由（1）可知，AE=GF，DC=BG，再由线段的和差和等量代换即可得到结论．【详解】（1）①证明：AB AC=B C∴∠=∠,60DF DE ADB=∠=︒，且E与A重合，ADF∴∆是等边三角形60ADF AFD∴∠=∠=︒120AFB ADC∴∠=∠=︒在ABF∆和ACD∆中AFB ADCB CAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩ABF ACD∴∆∆≌BF DC∴=②如图2，过点A做AG∥EF交BC于点G，∵∠ADB＝60°DE＝DF∴△DEF为等边三角形∵AG∥EF∴∠DAG＝∠DEF＝60°，∠AGD＝∠EFD＝60°∴∠DAG＝∠AGD∴DA＝DG∴DA－DE＝DG－DF，即AE＝GF由①易证△AGB≌△ADC∴BG＝CD∴BF＝BG＋GF＝CD＋AE（2）如图3，和（1）中②相同，过点A做AG∥EF交BC于点G，由（1）可知，AE=GF ，DC=BG ，BF CD BF BG GF AE ∴+=+==故BF AE CD =-．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．9．综合实践如图①，90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥，垂足分别为点D E 、，2.5, 1.7AD cm DE cm ==．（1）求BE 的长；（2）将CE 所在直线旋转到ABC ∆的外部，如图②，猜想AD DE BE 、、之间的数量关系，直接写出结论，不需证明；（3）如图③，将图①中的条件改为：在ABC ∆中，,AC BC D C E =、、三点在同一直线上，并且BEC ADC BCA α∠=∠=∠=，其中α为任意钝角．猜想AD DE BE 、、之间的数量关系，并证明你的结论．【答案】(1)0.8cm;(2)DE=AD+BE;(3)DE=AD+BE ，证明见解析．【解析】【分析】(1)本小题只要先证明ACD CBE ≅，得到AD CE =，CD BE =，再根据2.5, 1.7AD cm DE cm ==，CD CE DE =-，易求出BE 的值；(2)先证明ACD CBE ≅，得到AD CE =，CD BE =，由图②ED=EC+CD ，等量代换易得到AD DE BE 、、之间的关系；（３）本题先证明EBC DCA ∠=∠，然后运用“AAS”定理判定BEC CDA ≅，从而得到,BE CD EC AD ==，再结合图③中线段ED 的特点易找到AD DE BE 、、之间的数量关系．【详解】解：(1)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∵90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中，90ADC E ACD BCEAC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ 2.5, 1.7AD cm DE cm ==， 2.5 1.70.8()CD CE DE AD DE cm =-=-=-= ∴0.8BE cm =(2)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∴90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中，90ADC E ACD BCE AC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+(3)∵BEC ADC BCA α∠=∠=∠=∴180BCE ACD a ︒∠+∠=-180BCE BCE a ︒∠+∠=-∴ACD BCE ∠=∠在ACD与CBE△中，ADC E aACD BCEAC BC∠=∠=⎧⎪∠=∠⎨⎪=⎩∴ACD CBE≅∴,AD CE CD BE==又∵ED EC CD=+∴ED AD BE=+【点睛】本题考查的知识点是全等三角形的判定，确定一种判定定理，根据已知条件找到判定全等所需要的边相等或角相等的条件是解决这类题的关键．10．综合与实践：我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是，乐乐发现：当这两个三角形都是锐角三角形时，它们会全等.（1）请你用所学知识判断乐乐说法的正确性.如图，已知ABC∆、111A B C∆均为锐角三角形，且11AB A B=，11BC B C=，1C C∠=∠.求证：111ABC A B C∆∆≌.（2）除乐乐的发现之外，当这两个三角形都是______时，它们也会全等.【答案】（1）见解析；（2）钝角三角形或直角三角形.【解析】【分析】（1）过B作BD⊥AC于D，过B1作B1D1⊥B1C1于D1，得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°，根据SAS证△BDC≌△B1D1C1，推出BD=B1D1，根据HL证Rt△BDA≌Rt△B1D1A1，推出∠A=∠A1，根据AAS推出△ABC≌△A1B1C1即可．（2）当这两个三角形都是直角三角形时，直接利用HL即可证明；当这两个三角形都是钝角三角形时，与（1）同理可证.【详解】（1）证明：过点B作BD AC⊥于D，过1B作1111B D A C⊥于1D，则11111190BDA B D A BDC B D C ∠=∠=∠=∠=︒. 在BDC ∆和111B D C ∆中，1C C ∠=∠，111BDC B D C ∠=∠，11BC B C =， ∴111BDC B D C ∆∆≌，∴11BD B D =.在Rt BDA ∆和111Rt B D A ∆中，11AB A B =，11BD B D =，∴111Rt Rt (HL)BDA B D A ∆∆≌，∴1A A ∠=∠.在ABC ∆和111A B C ∆中，1C C ∠=∠，1A A ∠=∠，11AB A B =，∴111(AAS)ABC A B C ∆∆≌.（2）如图，当这两个三角形都是直角三角形时，∵11AB A B =，11BC B C =，190C C ∠==∠︒. ∴Rt ABC ∆≌111Rt A B C ∆（HL ）；∴当这两个三角形都是直角三角形时，它们也会全等； 如图，当这两个三角形都是钝角三角形时，作BD ⊥AC ，1111B D A C ⊥，与（1）同理，利用AAS 先证明111BDC B D C ∆∆≌，得到11BD B D =， 再利用HL 证明111Rt Rt BDA B D A ∆∆≌，得到1A A ∠=∠， 再利用AAS 证明111ABC A B C ∆∆≌；∴当这两个三角形都是钝角三角形时，它们也会全等；故答案为：钝角三角形或直角三角形.【点睛】本题考查了全等三角形的性质和判定的应用，主要考查学生的推理能力．解题的关键是熟练掌握证明三角形全等的方法.。

学大教育第1章全等三角形检测题〔本检测题总分值：100分，时间：90分钟〕一、选择题〔每题3分，共30分〕要测量河两岸相对的两点错误!未找到引用源。

的距离，先在错误!未找到引用源。

的垂线错误!未找到引用源。

上取两点错误!未找到引用源。

，使错误!未找到引用源。

，再作出错误!未找到引用源。

的垂线错误!未找到引用源。

，使错误!未找到引用源。

在一条直线上〔如下列图〕，可以说明△错误!未找到引用源。

≌△错误!未找到引用源。

，得错误!未找到引用源。

，因此测得错误!未找到引用源。

的长就是错误!未找到引用源。

的长，判定△错误!第1题图未找到引用源。

≌△错误!未找到引用源。

最恰当的理由是〔〕A.边角边B.角边角C.边边边D.边边角2.如下列图，两个全等的等边三角形的边长为1m，一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动，行走第2题图2 021m停下，那么这个微型机器人停在〔〕A.点A处B.点B处C.点C 处D.点E处3.如图，ABCDADBCAC与BD交于点AEBD于点ECFBD于点,，那么图中全等的三角形有( ) 对对对对4.以下命题中正确的选项是〔〕全等三角形的高相等全等三角形的中线相等全等三角形的角平分线相等全等三角形对应角的平分线相等如下列图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，那么以下结论不一定成立的是〔〕A.△ACE≌△BCDB. △BGC≌△AFCC.△DCG≌△ECFD. △ADB≌△CEA如下列图，错误!未找到引用源。

分别表示△ABC的三边长，那么下第3题图面与△错误!未找到引用源。

一定全等的三角形是〔〕第5题图第6题图7.：如下列图，B、C、D三点在同一条直线上，AC=CD，∠B=∠E=90°，1第7题图学大教育AC⊥CD，那么不正确的结论是〔〕A．∠A与∠D互为余角 B ．∠A=∠2C．△ABC≌△CED D ．∠1=∠2如下列图，两条笔直的公路错误!未找到引用源。

2021-2022年苏科版八年级数学上册《第1章全等三角形》单元能力提升训练（附答案）1．已知图中的两个三角形全等，则∠α的度数是（）A．72°B．60°C．58°D．50°2．如图，红红书上的三角形被墨迹污染了一部分，她根据所学的知识很快就画了一个与书上完全一样的三角形，那么红红画图的依据是（）A．SSS B．SAS C．ASA D．AAS3．下列说法正确的是（）A．全等三角形是指形状相同的两个三角形B．全等三角形的周长和面积分别相等C．全等三角形是指面积相等的两个三角形D．所有的等边三角形都是全等三角形4．如图，△ABC≌△EDF，DF＝BC，AB＝ED，AF＝20，EC＝10，则AE的长是．5．如图，△ABC≌△DCB，∠DBC＝40°，则∠AOB＝°．6．如图，BE⊥AC于点D，且AD＝CD，BD＝ED，若∠ABC＝54°，则∠E＝°．7．如图所示，已知AB＝AC，AE＝AF，AE⊥EC，AF⊥BF，垂足分别是点E、F．求证：∠1＝∠2．8．如图，AD⊥BC于D，AD＝BD，DC＝DE，∠1与∠C有什么关系？证明你的结论．9．如图，F是AD上一点，AB＝DE，AB∥DE，AF＝CD，求证：△ABC≌△DEF．10．完成下列推理过程：如图，已知点B，E在线段CF上，CE＝BF，AC∥FD，∠ABC＝∠DEF试说明：△ABC≌△DEF．解：因为CE＝BF（已知），所以CE﹣＝BF﹣（等式的性质），即＝．因为AC∥FD，所以∠＝∠．在△ABC和△DEF中，因为∠C＝∠F，BC＝EF，∠ABC＝∠DEF．所以△ABC≌△DEF（）．11．如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．求证：△AOB≌△COD．12．如图，已知AD＝AE，∠B＝∠C．求证：△ACD≌△ABE．13．如图，已知BD平分∠ABC，∠A＝∠C．求证：△ABD≌△CBD．14．如图，点B，E，C，F在同一条直线上，AB＝DE，BE＝CF，AB∥DE．求证：△ABC≌△DEF．15．已知：如图，AB＝AE，AB∥DE，∠ECB+∠D＝180°．求证：△ABC≌△EAD．16．如图，已知∠ABC＝∠BAD，∠C＝∠D，求证：△ABC≌△BAD．17．已知：如图，AC＝BD，∠1＝∠2．求证：△ADB≌△BCA．18．已知：如图，OA＝OD，OB＝OC．求证：△OAB≌△ODC．19．如图，已知点B，C，F，E在同一直线上，∠1＝∠2，BF＝CE，AB∥DE．求证：△ABC≌△DEF．20．如图，AB＝CB，BE＝BF，∠1＝∠2，证明：△ABE≌△CBF．21．如图，点D在AB上，点E在AC上，BE与CD相交于点O，AB＝AC，AD＝AE．求证：△BDC≌△CEB．22．已知，如图，点D，E分别在AB，AC上，∠B＝∠C，AB＝AC．求证：△AEB≌△ADC．23．如图，AC＝AE，∠1＝∠2，AB＝AD．求证：△ABC≌△ADE．24．如图，已知△ABC为等边三角形，D为BC延长线上的一点，CE平分∠ACD，CE＝BD，求证：（1）△ABD≌△ACE；（2）试判断△ADE的形状，并证明．参考答案1．解：∵图中的两个三角形全等a与a，c与c分别是对应边，那么它们的夹角就是对应角∴∠α＝50°故选：D．2．解：根据题意，三角形的两角和它们的夹边是完整的，所以可以利用“角边角”定理作出完全一样的三角形．故选：C．3．解：A、全等三角形的形状相同，但形状相同的两个三角形不一定是全等三角形．故该选项错误；B、全等三角形是指能够完全重合的两个三角形，则全等三角形的周长和面积一定相等，故B正确；C、全等三角形面积相等，但面积相等的两个三角形不一定是全等三角形．故该选项错误；D、两个等边三角形，形状相同，但不一定能完全重合，不一定全等．故错误．故选：B．4．解：∵△ABC≌△EDF，∴AC＝EF，∴AC﹣CE＝EF﹣CE，即AE＝CF，∵AF＝20，EC＝10，∴AE＝×（20﹣10）＝5．故答案为：5．5．解：∵△ABC≌△DCB，∠DBC＝40°，∴∠ACB＝∠DBC＝40°，∴∠AOB＝∠ACB+∠DBC＝40°+40°＝80°．故答案为：80．6．解：∵BE⊥AC，AD＝CD，∴AB＝CB，即△ABC为等腰三角形，∴BD平分∠ABC，即∠ABE＝∠CBE＝∠ABC＝27°，在△ABD和△CED中，，∴△ABD≌△CED（SAS），∴∠E＝∠ABE＝27°，故答案为：277．证明：∵AE⊥EC，AF⊥BF，∴△AEC是Rt△，△AFB是Rt△，在Rt△AEC与Rt△AFB中，，∴Rt△AEC≌Rt△AFB（HL），∴∠EAC＝∠F AB，∴∠EAC﹣∠BAC＝∠F AB﹣∠BAC，即∠1＝∠2．8．解：∠C＝∠1，理由如下：∵AD⊥BC，∴∠ADC＝∠BDE＝90°．又∵DC＝DE，AD＝BD，∴△ADC≌△BDE．∴∠C＝∠1．9．证明：∵AB∥DE，∴∠A＝∠D，∵AF＝DC，∴AF+FC＝DC+FC，即AC＝DF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．10．解：因为CE＝BF（已知），所以CE﹣BE＝BF﹣BE（等式的性质），即CB＝FE．因为AC∥FD，所以∠C＝∠F．在△ABC和△DEF中，因为∠C＝∠F，BC＝EF，∠ABC＝∠DEF．所以△ABC≌△DEF（ASA）．故答案为BE，BE；CB，FE；C，F；ASA．11．证明：∵∠AOC＝∠BOD，∴∠AOC﹣∠AOD＝∠BOD﹣∠AOD，即∠COD＝∠AOB，在△AOB和△COD中，，∴△AOB≌△COD（SAS）．12．证明：在△ACD和△ABE中，，∴△ACD≌△ABE（AAS）．13．证明：∵BD平分∠ABC，∴∠ABD＝∠CBD，在△ABD与△CBD中，，∴△ABD≌△CBD（AAS）．14．证明：∵BE＝CF，∴BE+EC＝CF+EC，即BC＝EF，又∵AB∥DE，∴∠B＝∠1，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．15．证明：∵AB∥DE，∴∠CAB＝∠E，∵∠ECB+∠D＝180°，∠ECB+∠ACB＝180°，∴∠D＝∠ACB，在△ABC与△EAD中，，∴△ABC≌△EAD（AAS）．16．证明：在△ABC和△BAD中，，∴△ABC≌△BAD（AAS）．17．证明：在△ADB和△BCA中，，∴△ADB≌△BCA（SAS）．18．证明：在△OAB和△ODC中，∴△OAB≌△ODC（SAS）．19．证明：∵BF＝CE，∴BF﹣FC＝CE﹣CF，即BC＝EF，∵AB∥DE，∴∠E＝∠B，在△ABC和△DEF中，，∴△ABC≌△DEF（ASA）．20．证明：∵∠1＝∠2，∴∠1+∠FBE＝∠2+∠FBE，即∠ABE＝∠CBF，在△ABE与△CBF中，，∴△ABE≌△CBF（SAS）．21．证明：∵AB＝AC，∴∠DBC＝∠ECB，∵AB＝AC，AD＝AE，∴BD＝CE，在△BDC和△CEB中，，∴△BDC≌△CEB（SAS）．22．证明：在△AEB和△ADC中，，∴△AEB≌△ADC（ASA）．23．证明：∵∠1＝∠2，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS），24．（1）证明：∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，AB＝AC，∴∠ACD＝120°，∵CE平分∠ACD，∴∠ACE＝∠DCE＝60°，∴∠B＝∠ACE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：△ADE是等边三角形，证明如下：由（1）得：△ABD≌△ACE，∴AD＝AE，∠BAD＝∠CAE，即∠BAC+∠CAD＝∠DAE+∠CAD，∴∠DAE＝∠BAC＝60°，∴△ADE为等边三角形．。

苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题，共计45分)1、如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）A. AB= DEB. AC= DFC.∠A=∠DD. BF= EC2、能判定△ABC≌△A′B′C′的条件是（）A.AB＝A′B′，AC＝A′C′，∠C＝∠C′B.AB＝A′B′，∠A＝∠A′，BC＝B′C′C.AC＝A′C′，∠A＝∠A′，BC＝B′C′D.AC＝A′C′，∠C＝∠C′，BC＝B′C′3、如图，在△ABC和△DBE中，AB=BC，DB=EB，∠ABC=∠DBE=50°.若∠BDC=25°，AD=4，DE= ，则CD的长为（）A. B. C. D.24、如图，在△ABD中，AD=AB，∠DAB=90⁰，在△ACE中，AC=AE，∠EAC=90⁰，CD，BE相交于点F，有下列四个结论：①DC=BE；②∠BDC=∠BEC；③DC⊥BE；④FA平分∠DFE.其中，正确的结论有（）A.4个B.3个C.2个D.1个5、如图，在正方形ABCD中，点G为CD边上一点，以CG为边向右作正方形CEFG，连结AF，BD交于点P，连结BG，过点F作FH∥BG交BC于点H，连结AH，交BD于点K，下列结论中错误的是（）A.HE=CDB.△AHF是等腰直角三角形C.点P为AF中点 D.PK=BK+DP6、如图为作一个角的角平分线的示意图，该作法的依据是全等三角形判定的基本事实，可简写为 ( )A.SSSB.SASC.ASAD.AAS7、如图，已知，下列结论：①；②；③；④；⑤；⑥；⑦.其中正确的有（）A. 个B. 个C. 个D. 个8、如图，已知的六个元素，则图甲、乙、丙三个三角形中和图全等的图形是（）．A.甲乙B.丙C.乙丙D.乙9、如图已知中，，，，点D为的中点.如果点P在线段上以的速度由B点向C点运动，同时，点Q在线段上由C点向A点运动.若点Q的运动速度为v，则当与全等时，v的值为（）A.1B.3C.1或3D.2或310、下列条件中，能判定△ABC≌△DEF的是（）A. ∠A=∠D，∠B=∠E，∠C=∠FB. AC=DF，∠B=∠E，BC=EF C. AB=DE，∠B=∠E，AC=DF D. AB=DE，∠B=∠E，BC=EF11、如图，AC⊥BC，BD⊥AD，垂足分别为C，D，再添加一个条件，仍不能判定△ABC≌△BAD的是（）A.AC＝BDB.AD＝BCC.∠ABD＝∠BACD.∠CAD＝∠DBC12、下列说法正确的是（）A.两角及一边分别相等的两个三角形全等B.到角两边距离相等的点在角的平分线上C.角的对称轴是角的平分线D.三角形三内角平分线的交点到三个顶点的距离相等13、如图，把长方形纸片沿对角线折叠，设重叠部分为.下列说法错误的是（）A. B. C. D.△ABE≌△CDE14、如图，公园里有一座假山，要测假山两端A，B的距离，先在平地上取一个可直接到达 A 和B的点C，分别延长AC，BC到D，E，使CD=CA ，CE=CB，连接DE．这样就可利用三角形全等，通过量出DE的长得到假山两端A，B的距离．其中说明两个三角形全等的依据是（）A.SSSB.ASAC.AASD.SAS15、如图，已知△ABC和△DCE均是等边三角形，点 B、C、E 在同一条直线上，AE与 BD交于点 O，AE与 CD交于点 G，AC与 BD交于点 F，连接 OC、FG，则下列结论要：①AE＝BD；②AG＝BF；③FG∥BE；④OC 平分∠BOE，其中结论正确的个数有（）A.1个B.2个C.3个D.4个二、填空题(共10题，共计30分)16、如图，△ABC≌△ADE，∠EAC=25°，则∠BAD= ________17、如图，在平面直角坐标系中，点A(2，0)，B(0，4)，作△BOC，使△BOC与△ABO全等，则点C坐标为________.18、如图，△ABC中（AB＞BC），G在CB的延长线上，边AC的垂直平分线DE 与∠ABG的角平分线交于点M，与AB交于点D，与AC相交于E，MN⊥AB于N.已知AB=13，BC=9，MN=3，则△BMN的面积是________.19、已知平面直角坐标系xOy中，点A、B的坐标分别为（1，0），（1，3），以A、B、P为顶点的三角形与△ABO全等，写出一个符合条件的点P的坐标：________20、如图，已知与是两个全等的直角三角形，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点B,C,F,D在同一条直线上，且点C与点F重合，将图（1）中的绕点C顺时针方向旋转到图（2）的位置，点E 在AB边上，AC交DE于点G，则∠ECG=________ 。

全等三角形解答题集中训练1.如图，已知△ABC 为等边三角形，点D、E 分别在边BC、AC 上，且AE＝CD，AD 与BE 相交于点F．(1)说明△ABE≌△CAD 的理由；(2)求∠BFD 的度数．2.如图(1)，已知点C 为线段AB 上一点，△ACM、△BCN 都是等边三角形．(1)求证：AN＝BM；(2)若把原题中“△ACM 和△BCN 是两个等边三角形”换成两个正方形(如图(2)所示），AN 与BM 的关系如何？请说明理由．3.如图，点C 在线段AB 上，DA⊥AB，EB⊥AB，FC⊥AB，且DA＝BC，EB＝AC，FC＝AB，∠AFB＝51°，求∠DFE 的度数．4.如图，在△ABC 中，D 是BC 的中点，DE⊥DF，试判断BE＋CF 与EF 的大小关系，并证明你的结论．5.如图，四边形ABCD 中，CD∥AB，E 是AD 中点，CE 交BA 延长线于点F．(1)试说明：CD＝AF；(2)若BC＝BF，试说明：BE⊥CF．6.一张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如图所示的形式，使点B、F、C、D 在同一条直线上．(1)求证：AB⊥ED；(2)若PB＝BC，请找出图中与此条件有关的一对全等三角形，并给予证明．7.已知在 Rt △ABC 中，AC ＝BC ，∠C ＝90°，D 为边 AB 的中点，∠EDF ＝90°，∠EDF绕点 D 旋转，它的两边分别交 AC 、CB(或它们的延长线)于点 E 、F ．当∠EDF 绕点 D 旋转到 DE ⊥AC 于点 E 时(如图(1))，易证 S △DEF ＋S △CEF ＝ 12S △ABC ．当∠EDF 绕点 D 旋转到 DE 和 AC 不垂直时，在图(2)和图(3)这两种情况下，上述结论是 否成立?若成立，请给予说明；若不成立，S △DEF 、S △CEF 、S △ABC 又有怎样的数量关系？请写出你的猜想，不需说明．8.数学作业本发下来了，徐波想：“我应该又是满分吧”，翻开作业本，一个大红的错号映入眼帘，徐波不解了，“我哪里做错了呢”？下面是题目和徐波的解法，亲爱的同学， 你知道他哪儿错了吗？你能帮他进行正确的说明吗？如图，∠BAC 是钝角，AB ＝AC ，D ，E 分别在 AB ，AC 上，且 CD ＝BE ．试说明∠ADC ＝ ∠AEB ． 徐波的解法：在△ACD 和△ABE 中，()()()AB AC BE CD BAE CAD =⎧⎪=⎨⎪∠=∠⎩已知已知公共角∴△ABE ≌△ACD ，∴∠ADC ＝∠AEB ．9.如图，已知直线l1∥l2，线段AB 在直线l1 上，BC 垂直于l1 交l2 于点C，且AB=BC，P 是线段BC 上异于两端点的一点，过点P 的直线分别交l2、l1 于点D、E（点A、E 位于点B 的两侧），满足BP=BE，连接AP、CE．（1）求证：△ABP≌△CBE；（2）连结AD、BD，BD 与AP 相交于点F．如图2．①当BCBP=2 时，求证：AP⊥BD；②当BCBP =n（n＞1）时，设△PAD 的面积为S1，△PCE 的面积为S2，求12SS的值．10.如图，在四边形ABCD 中，AB＝BC，BF 是∠ABC 的平分线，AF∥DC，连接ACCF．求证：CA 是∠DCF 的平分线．11.两个大小不同的等腰直角三角形三角板按图1 所示的位置放置，图2 是由它抽象出的几何图形，AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°，B，C，E 在同一条直线上，连接DC．(1)请找出图2 中与△ABE 全等的三角形，并给予证明（说明：结论中不得含有未标识的字母）；(2)证明：DC⊥BE．12.如图1，△ABC 的边BC 在直线l 上，AC⊥BC，且AC＝BC；△EFP 的边FP 也在直线l，边EF 与边AC 重合，且EF＝FP．(1)在图1 中，请你通过观察、测量，猜想并写出AB 与AP 所满足的数量关系和位置关系；(2)将△EFP 沿直线l 向左平移到图三的位置时，EP 交AC 于点Q，连接AP，BQ，猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；(3)将△EFP 沿直线x 向左平移到图3 的位置时，EP 的延长线交AC 的延长线于点Q，连接AP，BQ，你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗？若成立，请给出证明；若不成立，请说明理由．13.如图所示，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB 的度数．14.如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC.求证：（1）EC=BF；（2）EC⊥BF.15.在△ABC 中，∠ACB＝90°，AC＝BC，直线MN 经过点C，且AD⊥MN，BE⊥MN，垂足分别为点D，E．求证：DE＝AD＋BE．17.如图，在△ABC 中，∠ACB＝90°，AC＝BC，AE 是边BC 上的中线，过点C 作CF⊥AE，垂足为点F，过点B 作BD⊥BC 交CF 的延长线于点D．(1)求证：AE＝CD；(2)若AC＝12cm，求BD 的长．18.如图，已知CE⊥AB，BD⊥AC，垂足分别为点E，D，BD 与CE 交于点O，且AO 平分∠BAC．(1)图中有多少对全等三角形？请一一列举出来（不必说明理由）．(2)小明说：欲证BE＝CD，可先证明△AOF≌△AOD，得到AE＝AD，再证明△ADB≌△ AEC．得到AB＝AC，然后利用等式的性质得到BE＝CD，请问他的说法正确吗？如果正确，请按照他的说法写出推导过程；如果不正确，请说明理由．(3)要得到BE＝CD，你还有其他思路吗？若有，请写出推理过程．17.八年级(1)班同学到野外上数学活动课，为测量池塘两点A，B 的距离，设计了如下的方案：(I)如图①，先在平地上取一个可直接到达A，B 的点C，连接AC，BC，并分别延长AC 至点D，BC 至点E，使DC＝AC，EC＝BC，最后测出DE 的长即为AB 的距离；(Ⅱ)如图②，先过B 点作AB 的垂线BF，再在BF 上取C，D 两点使BC＝CD，接着过D 点作BD 的垂线DE，交AC 的延长线于点E，则测出DE 的长即为AB 的距离．阅读后回答下列问题：(1)方案(I)是否可行？；（填“可行”或“不可行”）(2)方案(Ⅱ)是否可行？请说明理由；(3)如果将方案(Ⅱ)中作BF⊥AB，ED⊥BF 改成满足∠ABD＝∠BDE≠90°，其他条件不变，方案(Ⅱ)是否可行？（直接回答即可，不必说明理由）18.在数学课本中我们研究过这样一道题目：(1)如图①，∠ACB＝90°，AC＝BC，BE⊥MN，AD⊥MN，垂足分别为E，D．图中哪条线段与AD 相等？(2)试问在图①这种情况下线段DE，AD，BE 具有怎样的等量关系？请写出来，不需要说明理由；(3)当直线CE 绕点C 旋转到图②中直线MN 的位置时，试问DE，AD，BE 具有怎样的等量关系？请写出这个等量关系，并说明理由．19.已知点P 是Rt△ABC 斜边AB 上一动点（不与点A，B 重合）分别过点A，B 向直线CP 作垂线，垂足分别为点E，F，Q 为斜边AB 的中点．(1)如图1，当点P 与点Q 重合时，AE 与BF 的位置关系是，QE 与QF 的数量关系是；(2)如图2，当点P 在线段AB 上不与点Q 重合时，试判断QE 与QF 的数量关系，并给予证明；(3)如图3，当点P 在线段BA(或AB)的延长线上时，此时(2)中的结论是否成立？请画出图形并给予证明．20.如图，在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于点F，连接CF．求证：(1) AF=CD；(2) ∠AFC=∠CDA．21.如图，在四边形ABCD 中，AB=DC，延长线段CB 到E，使BE=AD，连接AE，AC，AE=AC．求证：(1) △ABE≌△CDA；(2) AD∥EC．22.如图，点M，N 分别是正五边形ABCDE 的边BC，CD 上的点，且BM=CN，AM 交BN 于点P．(1) 求证：△ABM≌△BCN；(2) 求∠APN 的度数．23.已知：如图，在△ABC 中，DE、DF 是△ABC 的中位线，连接EF、AD，其交点为O．求证：（1）△CDE≌△DBF；（2）OA=O D．24..如图1，在△ABC 中，∠BAC 为直角，点D 为射线BC 上一点，连接AD，以AD 为一边且在AD 的右侧作正方形ADEF．如图(1),则∠BAD =∠(2)若AB=AC，①当点D 在线段BC 上时（与点B 不重合），如图2，问CF、BD 有怎样的关系?并说明理由.②当点D 在线段BC 的延长线上时，如图3，①中的结论是否仍然成立，直接写出结论.(10分)25.如图，已知正方形ABCD 中，边长为10cm，点E 在AB 边上，BE＝6cm．(1)如果点P 在线段BC 上以4cm/秒的速度由B 点向C 点运动，同时，点Q 在线段CD 上以acm/秒的速度由C 点向D 点运动，设运动的时间为t 秒，①CP 的长为cm（用含t 的代数式表示）；②若以E、B、P 为顶点的三角形和以P、C、Q 为顶点的三角形全等，求a 的值．(2)若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿正方形ABCD 四边运动．则点P 与点Q 会不会相遇？若不相遇，请说明理由．若相遇，求出经过多长时间点P 与点Q 第一次在正方形ABCD 的何处相遇？。

第一章全等三角形单元练习题七1．如图，AD是角平分线，E是AB上一点，AE=AC，EF∥BC交AC于F．以下结论①△ADC≌△ADE；②CE平分∠DEF；③AD垂直平分CE．其中正确的选项是〔〕A．①②③ B．① C．② D．③2．△ABC≌△A′B′C′，其中∠A′=50°，∠B′=70°，那么∠C的度数为〔〕A． 55° B． 60° C． 70° D． 75°3．如图，△ABC≌△CDA，AB=4，BC=6，AC=5，那么AD的长为〔〕A． 4 B． 5 C． 6 D．不确定4．如图是5×5的正方形的网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出〔〕A ． 2个B ． 3个C ． 4个D ． 5个5．如图，在矩形ABCD 中， 2BC AB =， ADC ∠的平分线交边BC 于点E ， AH DE ⊥于点H ，连接CH 并延长交边AB 于点F ，连接AE 交CF 于点O .给出以下命题：①AEB AEH ∠=∠；②22DH EH =；③12HO AE =；④2BC BF EH -=.其中正确命题为〔 〕A ． ①②B ． ①③C ． ①③④D ． ①②③④6．如图，在△PAB 中，P A ＝PB ，M ，N ，K 分别在PA ，PB ，AB 上，且AM ＝BK ，BN ＝AK ，假设∠MKN ＝40°，那么∠P 的度数为〔 〕A ． 140° B． 90° C． 100° D． 110°7．如图，△ABC 中，∠A=90°，AB=AC ，BD 平分∠ABE ，DE ⊥BC ，假设△DEC 的周长是10cm ，那么BC=〔 〕A ． 8cmB ． 10cmC ． 11cmD ． 12cm8．如图，，添加以下条件还不能．．判定≌的是A． B． C． D．9．如下图，∠E=∠F，∠B=∠C，AE=AF，以下结论：①∠FAN=∠EAM；②EM=FN；③△ACN≌△ABM；④CD=DN．其中正确的有〔〕A． 1个 B． 2个 C． 3个 D．4个10．以下条件中，不能判定两个直角三角形全等的是( )A．两条直角边对应相等 B．有两条边对应相等C．斜边和一锐角对应相等 D．一条直角边和斜边对应相等11．在如下图的4×4正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝_____．12．如图，在△ABC和△DEF中，B，E，C，F在同一条直线上，下面有四个条件：①AB＝DE，②AC＝DF，③∠ABC＝∠DEF，④BE＝CF．请你在其中选3个作为题设，余下的1个作为结论，写出所有能组成真命题组合的题设．．为__________________．〔填序号〕13．课间，顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图)，直角顶点H的坐标为(0，1)，另一个顶点G的坐标为(4，4)，那么点K的坐标为___________14．如图，AB ⊥BD 于B ，ED ⊥BD 于D ，AB=CD,AC=CE ，那么∠ACE=__________°.15．如图，△ABE 和△ACF 分别是以△ABC 的AB 、AC 为边的等边三角形，CE 、BF 相交于O ，那么∠EOB=___°．16．如图，在正方形ABCD 中，AC 为对角线，E 为AB 上一点，过点E 作EF ∥AD ，与AC 、DC 分别交于点G 、F ，H 为CG 的中点，连接DE 、EH 、DH 、FH ．以下结论：①EG=DF ；②∠AEH+∠ADH=180°；③△EHF ≌△DHC ；④假设13AE AB =，那么3S △EDH =13S △DHC ，其中结论正确的有________〔填写序号〕.17．如图，AB =AD ，只需添加一个条件___________________，就可以判定△ABC ≌△ADE ．18．如图，四边形ABCD 中， AB AD BD ==， 2AC AB =， 30BCD ∠=︒，那么线段BC 、BD 、CD 之间的重量关系是__________．19．如图，己知AC=BD，CF=DE，点A、E、F、B在同一条直线上，要使△ACF≌△BDE，还要添加一个条件，添加的这个条件可以是______.20．如图，AD∥BC，AB∥DC，那么全等三角形共有______对.21．，如图，延长的各边，使得，，顺次连接，得到为等边三角形．求证：〔1〕；〔2〕为等边三角形．22．四边形 ABCD 中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=1200，∠MBN=600，将∠MBN 绕点B 旋转．当∠MBN 旋转到如图的位置，此时∠MBN 的两边分别交 AD、DC 于 E、F，且AE≠CF.延长 DC 至点 K，使 CK=AE，连接BK．求证：〔1〕△ABE≌△CBK；〔2〕∠KBC+∠CBF=600 ；〔3〕CF+AE=EF．23．正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD 于点F．如图1，当点P与点O重合时，显然有DF=CF．〔1〕如图2，假设点P在线段AO上〔不与点A、O重合〕，PE⊥PB且PE交CD于点E．求证：DF=EF；〔2〕假设点P在线段OC上〔不与点O、C重合〕，PE⊥PB且PE交直线CD于点E．请完成图3并判断〔1〕中的结论是否成立？请说明理由．24．如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8.点P从点A出发沿路径A→C→B向终点B运动；点Q从点B出发沿路径B→C→A向终点A运动．点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动，两点都要到相应的终点时才能停止运动，在某一时刻，过点P作PE⊥l于点E，过点Q作QF⊥l于点F.问：点P运动多少时间时，△PEC与△CFQ 全等？请说明理由．25．如下图，△BDC中，AB=8cm，AC=6cm，AD为BC边上的中线，求中线AD的取值范围. 26．如图，点F、C在BE上，BF=CE，AB=DE，∠B=∠E.求证：∠A=∠D．27．〔1〕如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，求证：EF=BE+FD．〔2〕如图2，四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，那么当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD，说明理由．〔3〕如图3，四边形ABCD中，∠BAD≠90°，AB=AD，AC平分∠BCD，AE⊥BC于E，AF⊥CD 交CD延长线于F，假设BC=8，CD=3，那么CE= .〔不需证明〕28．如图，桌面上竖直放置一等腰直角三角板ABC，假设测得斜边AB的两端点到桌面的距离分别为AD,BE. DE为8cm，BE=3cm，求点A距离桌面的高度．。

苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题，共计45分)1、如图，在下列条件中，不能证明△ABD≌△ACD的条件是（）A.∠B=∠C，BD=DCB.∠ADB=∠ADC，BD=DCC.∠B=∠C，∠BAD=∠CADD.BD=DC，AB=AC2、直线l上有三个正方形A、B、C放置如图所示，若正方形A、C的面积分别为1和12，则正方形B的面积为（）．A.11B.12C.13D.3、下列各组图形中，是全等形的是（）A.两个含60º角的直角三角形B.腰对应相等的两个等腰直角三角形 C.有一腰和一角相等的两个等腰三角形 D.一个钝角相等的两个等腰三角形4、如图，AB∥CD，AD∥BC，EF过点O，图中全等三角形共有（）A.2对B.4对C.6对D.8对5、如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（）A.BD=CDB.AB=ACC.∠B=∠CD.∠BAD=∠CAD6、下列命题：①关于某条直线成轴对称的两个图形是全等图形；②有一个外角为60°的等腰三角形是等边三角形；③关于某直线对称的两条线段平行；④正五边形有五条对称轴；⑤在直角三角形中，30°角所对的边等于斜边的一半．其中正确的有（）个．A.1个B.2个C.3个D.4个7、已知，，且的周长为20，，，则等于（）A.3B.5C.9D.118、下列说法中，不正确的是（）①全等形的面积相等；②形状相同的两个三角形是全等三角形；③全等三角形的对应边，对应角相等；④若两个三角形全等，则其中一个三角形一定是由另一个三角形旋转得到的．A.①与②B.③与④C.①与③D.②与④9、用直尺和圆规作一个角等于已知角的示意图如下，则说明∠A′O′B′=∠AOB的依据是（）A.SSSB.SASC.ASAD.AAS10、如图，△ABC≌△DEF，BC＝7，EC＝4，则CF的长为（）A.2B.3C.5D.711、如图，△ABC≌△ADE，∠DAC=60 ，∠BAE=100 ,BC，DE相交于点F,则∠DFB度数是( )A.15B.20C.25D.3012、如图，已知△ABC≌△ADC，∠B＝30°，∠BAC＝23°，则∠ACD的度数为（）A.120°B.125°C.127°D.104°13、在△ABC和△EMN中，已知∠A=50°，∠B=60°，∠E=70°，∠M=60°，AC=EN，则这两个三角形（）A.一定全等B.一定不全等C.不一定全等D.以上都不对14、如图，点D在AB上，点E在AC上，AB＝AC添加下列一个条件后，还不能证明△ABE≌△ACD的是（）A.AD＝AEB.BD＝CEC.∠B＝∠CD.BE＝CD15、如图，在中，，，，垂足为点，过点作射线，点是边上任意一点，连接并延长与射线相交于点，设，两点之间的距离为，过点作直线的垂线，垂足为．岑岑同学思考后给出了下面五条结论，正确的共有（）①；②当时，；③当时，四边形是平行四边形；④当或时，都有；⑤当时，与一定相似．A.2条B.3条C.4条D.5条二、填空题(共10题，共计30分)16、在△ABC中，AC＝5，中线AD＝4，则边AB的取值范围是________.17、如图，在锐角三角形ABC中，，，点D为边AB的中点，点E在边AC上，将沿DE折叠得到.若，则的值为________；的值为________.18、如图，正方形ABCD中，BE平分∠ABD交AD于E，EF⊥BD于F，FP⊥AB于P，已知正方形ABCD的边长BC＝2，则AP的长是________．19、如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是________ （只写一个条件即可）.20、如图，在正方形中，，延长到点，使，连接，动点从点出发以每秒个单位的速度沿向终点运动，设点的运动时间为秒，当和全等时，的值为________．21、如图，直线y＝2x﹣1分别交x，y轴于点A，B，点C在x轴的正半轴，且∠ABC＝45°，则直线BC的函数表达式是________．22、如图，△ABD≌△ABC，∠C=100°，∠ABD=30°，则∠DAC=________．23、如图，AD是ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE．下列说法：①CE＝BF；②ABD和ACD面积不相等；③BF∥CE；④BDF≌CDE．其中正确的有________(填序号)．24、如图，已知AB∥CF，E为DF的中点，若AB=13cm，CF=9cm，则BD=________cm．25、以线段AC为对角线的四边形ABCD(它的四个顶点A，B，C，D按顺时针方向排列)，已知AB＝BC＝CD，∠ABC＝100°，∠CAD＝40°，则∠BCD的度数为________．三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、已知：如图，点P是ABCD的对角线AC的中点，经过点P的直线EF交AB于点E，交DC于点F．求证：AE＝CF．28、易知周长相等的两圆相同，周长相等的两个正方形相同，那么，周长相等的两个三角形全等吗？29、已知：如图，E，F是▱ABCD的对角线AC上两点，且AE＝CF.求证：BE＝DF.30、如图，在△ABC中，点E在BC上，点D在AE上，已知∠ABD=∠ACD，∠BDE=∠CDE．求证：BD=CD．参考答案一、单选题(共15题，共计45分)1、A2、C3、B4、C5、B6、C7、C9、A10、B11、B12、C13、A14、D15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。