相似三角形的应用题

相似三角形的应用经典练习题三套A卷：1、在阳光下，身高1.68m的小强在地面上的影长为2m，在同一时刻，测得学校的旗杆在地面上的影长为18m．则旗杆的高度为(精确到0.1m)．2、如图，在河两岸分别有A、B两村，现测得A、B、D在一条直线上，A、C、E在一条直线上，BC//DE，DE=90米，BC=70米，BD=20米。

则A、B两村间的距离为。

3、（06湖州）为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据《科学》中光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树（AB）的高度约为________米（精确到0.1米）。

4、如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，求电视塔的高ED。

5、小强用这样的方法来测量学校教学楼的高度：如图，在地面上放一面镜子（镜子高度忽略不计），他刚好能从镜子中看到教学楼的顶端B，他请同学协助量了镜子与教学楼的距离EA=21米，以及他与镜子的距离CE=2.5米，已知他的眼睛距离地面的高度DC=1.6米，请你帮助小强计算出教学楼的高度。

（根据光的反射定律：反射角等于入射角）6、某数学课外实习小组想利用树影测量树高，他们在同一时刻测得一身高为1.5米的同学的影子长为1.35米，因大树靠近一栋建筑物，大树的影子不全在地面上，他们测得地面部分的影子长BC=3.6米，墙上影子高CD=1.8米，求树高AB。

7、如图,甲楼AB 高18米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是 ,已知两楼相距20米,那么甲楼的影子落在乙楼上有多高?8、为了测量路灯（OS ）的高度,把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC ）长为1米,然后拿竹竿向远离路灯方向走了4米（BB ‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B ‘C ‘）为1.8米,求路灯离地面的高度.9、如图，有一路灯杆AB(底部B 不能直接到达)，在灯光下，小明在点D 处测得自己的影长DF ＝3m ，沿BD 方向到达点F 处再测得自己得影长FG ＝4m ，如果小明得身高为1.6m ，求路灯杆AB 的高度。

人教版九年级数学下册27.2.3 相似三角形应用举例达标训练一、单选题1．如图，阳光从教室的窗户射入室内，窗户框AB 在地面上的影子长DE ＝1.8m ，窗户下沿到地面的距离BC＝1m ，EC ＝1.2m ，那么窗户的高AB 为（ ）A ．1.5mB ．1.6mC ．1.86mD ．2.16m2．某班某同学要测量学校升旗的旗杆高度，在同一时刻，量得某一同学的身高是1.5m ，影长是1m ，旗杆的影长是8m ，则旗杆的高度是（ ） A ．12mB ．11mC ．10mD ．9m3．如图，王华晚上由路灯A 下的B 处走到C 处时，测得影子CD 的长为1 m ，继续往前走3 m 到达E 处时，测得影子EF 的长为2 m.已知王华的身高是1.5 m ，那么路灯A 的高度AB 等于( )A ．4.5 mB ．6 mC ．7.2 mD ．8 m4．如图，身高为1.6m 的某学生想测量一棵大树的高度，她沿着树影BA 由B 到A 走去，当走到C 点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m ，CA=0.8m ，则树的高度为（ ）A ．4.8mB ．6.4mC ．8mD ．10m5．如图，小明晚上由路灯A 下的点B 处走到点C 处时，测得自身影子CD 的长为1米，他继续往前走3米到达点E 处（即CE=3米），测得自己影子EF 的长为2米，已知小明的身高是1.5米，那么路灯A 的高度AB 是（ ）A ．4.5米B ．6米C ．7.2米D ．8米6．如图所示的梯形梯子，AA′∥EE′，AB=BC=CD=DE ，A′B′=B′C′=C′D′=D′E′，AA′=60cm ，EE′=80cm ．则BB′的长为（ ）A ．0.65mB ．0.675mC ．0.725mD ．0.75m7．现有一个测试距离为5m 的视力表（如图），根据这个视力表，小华想制作一个测试距离为3m 的视力表，则图中的ab的值为（ ）A ．32B ．23C ．35D ．538．如图，A 、B 两点被池塘隔开，在AB 外任选一点C ，连接AC，BC分别取其三等分点M，N ，量得MN=38m ．则AB 的长是（ ）A ．76mB ．104mC ．114mD ．152m二、填空题9．图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB=cm10．小明在离路灯底部6m 处测得自己的影子长为1.2m ，小明的身高为1.6m ，那么路灯的高度为m .11．如图，AB 是斜靠在墙角的长梯，梯角B 距墙0.8m ，长梯上一点D 距墙0.7m ，BD 长0.55m ，则梯子的长度是 m ．12．如图，某风景区在建设规划过程中，需要测量两岸码头A 、B 之间的距离．设计人员在O 点设桩，取OA 、OB 的三等分点C 、D ，测得CD=25m ，则AB= ．13．为测量操场上悬挂国旗的旗杆的高度，设计的测量方案如图所示：标杆高度CD=3m ，标杆与旗杆的水平距离BD=15 m ，人的眼睛与地面的高度EF=1.6m ，人与标杆CD 的水平距离DF=2m ，E 、C 、A 三点共线，则旗杆AB 的高度为 米．14．如图；课外活动小组测量学校旗杆的高度．如图，在地面上C 处放一小镜子，当镜子离旗杆AB 底端6米，小明站在离镜子3米的E 处，恰好能看到镜子中旗杆的顶端，测得小明眼睛D 离地面1.5米，则旗杆AB 的高度约是 米．三、解答题15．如图，要测量河岸相对的两点A 、B 的距离，先从点B 出发与AB 成90°角方向，向前走50m 到C 处立一根标杆，然后方向不变继续朝前走10m 到D 处，在D 处转90°沿DE 方向再走17m ，这时A 、C 、E 在同一直线上．问A 、B 间的距离约为多少？16．如图，某人在点A 处测量树高，点A 到树的距离AD 为21米，将一长为2米的标杆BE 在与点A 相距3米的点B 处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树的顶点C，求树CD的高．17．又到了一年中的春游季节．某班学生利用周末去参观“三军会师纪念塔”．下面是两位同学的一段对话：甲：我站在此处看塔顶仰角为60°； 乙：我站在此处看塔顶仰角为30°； 甲：我们的身高都是1.6m ； 乙：我们相距36m ．请你根据两位同学的对话，计算纪念塔的高度．（精确到1米）18．如图，已知∥ABC 的面积S ∥ABC =1.在图（1）中，若11112AA BB CC AB BC CA ===， 则11114A B C S =； 在图（2）中，若22213AA BB CC AB BC CA ===， 则22213A B C S =； 在图（3）中，若33314AA BB CC AB BC CA ===， 则333716A B C S =； 按此规律，若44415AA BB CC AB BC CA ===， 则444A B C S = 若88819AA BB CC AB BC CA ===， 则888A B C S = . 19．如图，在直角梯形ABCD 中，AD∥BC ，∥A=90°，BD∥CD ，垂足为D ．（1） 若AD=9，BC=16，求BD 的长； （2） 求证：AB 2•BC=CD 2•AD ．答案解析部分1．【答案】A【解析】【解答】∵BE∥AD，∴∥BCE∥∥ACD，∴CB CEAC CD=，即CB CEAB BC DE EC=++，∵BC=1，DE=1.8，EC=1.2∴1 1.21 1.8 1.2 AB=++∴1.2AB=1.8，∴AB=1.5m．故答案为：A．【分析】先证明∥BCE∥∥ACD，再利用相似三角形的性质可得CB CEAC CD=，即CB CEAB BC DE EC=++，再将数据代入计算可得1 1.21 1.8 1.2AB=++，最后求出AB的长即可。

相似三角形的应用精选练习题1.XXX用自制的直角三角形纸板DEF测量树AB的高度。

测量时，使直角边DF保持水平状态，其延长线交AB于点G；使斜边DE所在的直线经过点A。

测得边DF离地面的高度为1m，点D到AB的距离等于7.5m。

已知DF=1.5m，EF=0.6m，求树AB的高度。

2.XXX测得2m高的标杆在太阳下的影长为1.2m，同时又测得一棵树的影长为3.6m。

请计算这棵树的高度。

3.XXX用下面的方法来测量学校教学大楼AB的高度。

在水平地面点E处放一面平面镜，镜子与教学大楼的距离AE=20米。

当她与镜子的距离CE=2.5米时，她刚好能从镜子中看到教学大楼的顶端B。

已知她的眼睛距地面高度DC=1.6米，请帮助小红测量出大楼AB的高度（注：入射角=反射角）。

5.XXX在晚上由路灯A走向路灯B。

当他走到点P时，发现他身后影子的顶部刚好接触到路灯A的底部；当他向前再步行12m到达点Q时，发现他身前影子的顶部刚好接触到路灯B的底部。

已知XXX的身高是1.6m，两个路灯的高度都是9.6m，且AP=QB。

1) 求两个路灯之间的距离。

2) 当XXX走到路灯B的底部时，他在路灯A下的影长是多少？6.某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度。

他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上。

已知DE=0.5米，EF=0.25米，目测点D到地面的距离DG=1.5米，到旗杆的水平距离DC=20米，求旗杆的高度。

7.△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm。

在BC边上取一点E，使AE=CD。

连接DE，求DE的长度。

8.晚饭后，小聪和小军在社区广场散步，小聪问小军：“你有多高？”小军一时语XXX。

XXX想到了一个办法，他找到一面墙，让小军站在墙边，然后用一支笔在墙上画出小军头顶的位置，再测量墙顶到地面的距离，就能算出小军的身高了。

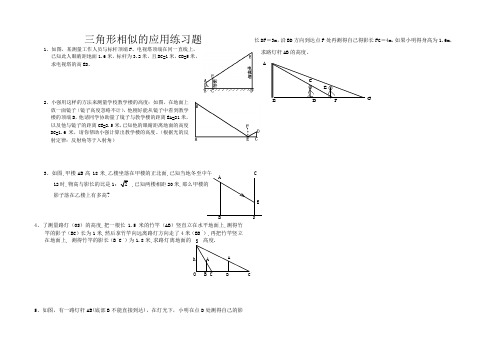
三角形相似的应用练习题
1、如图，某测量工作人员与标杆顶端F 、电视塔顶端在同一直线上，
已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，
求电视塔的高ED 。

2、小强用这样的方法来测量学校教学楼的高度：如图，在地面上放一面镜子（镜子高度忽略不计），他刚好能从镜子中看到教学楼的顶端B ，他请同学协助量了镜子与教学楼的距离EA=21米，
以及他与镜子的距离CE=2.5米，已知他的眼睛距离地面的高度
DC=1.6米，请你帮助小强计算出教学楼的高度。

（根据光的反
射定律：反射角等于入射角）
3、如图,甲楼AB 高18米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是
1: 已知两楼相距20米,
那么甲楼的影子落在乙楼上有多高?
4、了测量路灯（OS ）的高度
,把一根长1.5米的竹竿（AB ）竖直立在水平地面上,测得竹竿的影子（BC ）长为1米,然后拿竹竿向远离路灯方向走了4米（BB ‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B ‘C ‘）为1.8米,求路灯离地面的高度.
5、如图，有一路灯杆AB(底部B 不能直接到达)，在灯光下，小明在点D 处测得自己的影长DF ＝3m ，沿BD 方向到达点F 处再测得自己得影长FG ＝4m ，如果小明得身高为1.6m ，求路灯杆AB 的高度。

A h S A C B B 'O C 'A 'E D
C A G。

利用相似三角形求解问题的练习题相似三角形是几何学中重要的概念之一，应用相似三角形的性质可以帮助我们解决许多问题。

以下是一些利用相似三角形求解问题的练习题，希望能帮助读者更好地理解和掌握这一概念。

练习题一：已知直角三角形ABC，其中∠C为直角，AB=5cm，AC=12cm。

在AB边上选一点D，连接CD并延长至与BC边交于点E。

若BD=DE，求CE的长度。

解答：由于∠C为直角，则∠CAB和∠CBA分别为对角ABC和ACB的对应角，即∠CAB∽∠ACB。

又因为BD=DE，所以可以得到∠BDC=∠CDE，同理有∠CBD=∠CED。

根据相似三角形的性质，可以得到以下比例关系：AB/AC = BD/CE代入已知数值，可得：5/12 = BD/CE解方程，可得：CE = (12/5) * BD由题目可知BD=DE，所以BD=5cm，代入可得：CE = (12/5) * 5 = 12cm所以CE的长度为12cm。

练习题二：在平面直角坐标系中，已知三角形ABC，其中A(-2,4)、B(1,2)、C(4,-2)，直线DE与x轴和y轴分别交于点D(5,0)和E(0,-4)，求证：△ABC∽△ADE，并计算其相似比。

解答：首先，计算△ABC和△ADE的边长：△ABC的边长：AB = √[(1-(-2))^2 + (2-4)^2] = √[3^2 + (-2)^2] = √13BC = √[(4-1)^2 + (-2-2)^2] = √[3^2 + 4^2] = 5AC = √[(4-(-2))^2 + (-2-4)^2] = √[6^2 + (-6)^2] = 6√2△ADE的边长：AD = √[(-2-5)^2 + (4-0)^2] = √[(-7)^2 + 4^2] = √65DE = √[(-2-0)^2 + (4-(-4))^2] = √[(-2)^2 + 8^2] = 2√4 = 4AE = √[(-2-0)^2 + (4-0)^2] = √[(-2)^2 + 4^2] = 2√5可以发现，AB/AD = 1/√5，BC/DE = 5/4，AC/AE = √2/√5。

初中数学相似三角形应用题及答案相似三角形是初中数学中的一个重要概念，通过相似三角形的性质和应用，我们可以解决很多实际问题。

本文将介绍几个常见的相似三角形应用题，并给出详细的解答。

1. 题目：甲地点的高楼上立有一块长度为6厘米的广告牌，乙地点的高楼上立有一块长度为8厘米的广告牌。

测得甲地点的高楼到乙地点的高楼的水平距离为12米。

求甲地点的高楼到乙地点的高楼的实际距离。

解答：我们可以构建两个相似三角形，分别是甲地点的高楼到广告牌的距离和甲地点的高楼到乙地点的高楼的距离。

设甲地点的高楼到广告牌的距离为x米，则根据相似三角形的性质有：x/6 = 12/8通过交叉相乘得到6x = 12*8，化简得到x = 16米。

因此，甲地点的高楼到乙地点的高楼的实际距离为16米。

2. 题目：甲、乙两地相距120公里。

已知甲地点的高楼高度为80米，乙地点的高楼高度为60米。

测得甲地点的高楼顶与乙地点的高楼顶的仰角为30度。

求甲地点的高楼底与乙地点的高楼底的水平距离。

解答：我们可以构建两个相似三角形，分别是甲地点的高楼到乙地点的高楼的距离和甲地点高楼的高度与乙地点高楼的高度的距离。

设甲地点的高楼底与乙地点的高楼底的水平距离为x米，则根据相似三角形的性质有：x/120 = 80/60通过交叉相乘得到60x = 120*80，化简得到x = 160米。

因此，甲地点的高楼底与乙地点的高楼底的水平距离为160米。

3. 题目：已知一艘船从A地点出发，以每小时20公里的速度顺水行驶，到达B地点。

然后从B地点回到A地点，以每小时16公里的速度逆水行驶。

整个行程共花费10小时。

求从A地点到B地点的距离。

解答：我们可以构建两个相似三角形，分别是从A地点到B地点的距离与船行驶的时间。

设从A地点到B地点的距离为x公里，则根据相似三角形的性质有：x/(20-16) = (10-10)/10通过交叉相乘得到4x = 0，化简得到x = 0公里。

因此，从A地点到B地点的距离为0公里。

相似三角形的应用及位似（习题）➢例题示范例1：小红用下面的方法来测量学校教学大楼AB 的高度：如图在水平地面点E 处放一面平面镜，镜子与教学大楼的距离AE=20 米．当她与镜子的距离CE=2.5 米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1.6 米，请你帮助小红测量出大楼AB 的高度（注：入射角=反射角）．解：由题意，AE=20，CE=2.5，DC=1.6，∠FEB=∠FED∴∠BEA=∠DEC∵∠BAE=∠DCE=90°∴△BAE∽△DCE∴ AB=AEDC EC∴ AB=201.62.5∴AB=12.8∴大楼AB 的高为12.8 米．例2：如图，某一时刻，旗杆AB 的影子一部分在地面上，另一部分在建筑物的墙面上．小明测得旗杆AB 在地面上的影长BC 为9.6 m，在墙面上的影长CD 为2 m．同一时刻，小明又测得竖立于地面长1 m 的标杆的影长为1.2 m．请帮助小明求出旗杆的高度．解：如图，过点D 作DE∥BC 交AB 于点E，则四边形BCDE 为矩形．由题意，BC=9.6，CD=2，∴BC=DE=9.6，CD=BE=2由题意，AE=ED1 1.2∴AE=8∴AB=AE+EB=8+2=10∴旗杆的高度为10 m．➢巩固练习1.如图，AB∥CD，AD，BC 相交于点E，过E 作EF∥AB 交BD于点F，则图中相似的三角形有对．2.如图是测量河宽的示意图，AE 与BC 相交于点D，∠B=∠C=90°，测得BD=120 m，DC=60 m，EC=50 m，求得河宽AB= m．3.如图，在同一时刻，小明测得他的影长为1 m，距他不远处的一棵槟榔树的影长为5 m，若小明的身高为1.5 m，则这棵槟榔树的高度是．4.“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（）A．1.25 尺B．57.5 尺C．6.25 尺D．56.5 尺5.小刚身高1.7 m，测得他站立在阳光下的影子长为0.85 m，紧接着他把手臂竖直举起，测得影子长为1.1 m，那么小刚举起的手臂超出头顶（）A．0.5 m B．0.55 m C．0.6 m D．2.2 m 6.如图是小明设计的用手电筒来测量某古城墙高度的示意图．点P 处放一水平的平面镜，光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处，已知AB⊥BD，CD⊥BD，且测得AB=1.2 m，BP=1.8 m，PD=12 m，那么该古城墙的高度是（）A．8 m B．10 mC．15 m D．18 m7.如图5，小明同学用自制的直角三角形纸板EFG 测量树的高度AB，他调整自己的位置，设法使斜边EG 保持水平，并且边EF 所在的直线经过点A，已知纸板的两条直角边EF=60 cm，FG=30 cm，测得小明与树的水平距离BD=8 m，边EG 离地面的高度DE=1.6 m，则树高为．8.如图，一同学在某时刻测得1 m 长的标杆竖直放置时影子长为1.6 m，同一时刻测量旗杆的影子长时，因旗杆靠近一栋楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影子长为11.2 m，留在墙上的影子高为1 m，则旗杆的高度是．第8 题图第9 题图9.如图，小明想测量电线杆AB 的高度，发现电线杆的影子恰好落在土坡的坡面CD 和地面BC 上，量得CD=4 m，BC=10 m，CD 与地面成30°角，且此时测得1 m 杆的影子长为2 m，则电线杆的高度为．10.如图，在斜坡的顶部有一竖直铁塔AB，B 是CD 的中点，且CD 是水平的．在阳光的照射下，塔影DE 留在坡面上，已知铁塔底座宽CD=14 m，塔影长DE=36 m，小明和小华的身高都是1.6 m，小明站在点E 处，影子也在斜坡面上，小华站在沿DE 方向的坡脚下，影子在平地上，两人的影长分别为4 m，2 m，那么塔高AB= ．第10 题图第11 题图11.某兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1 m 的竹竿的影长为0.4 m，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2 m，一级台阶高为0.3 m，如图所示，若此时落在地面上的影长为4.4 m，则树高为．12.如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A′B′C′D′E′，已知OA=10 cm，OA'=20 cm，则五边形ABCDE 的周长与五边形A′B′C′D′E′的周长比是．13.如图，△ABC 与△DEF，且直线AD，CF，BE 相交于点O，OA=OB=OC=2，已知AB=4，则DE 的长为．OD OE OF 314.如图，在△ABC 中，A，B 两个顶点在x 轴的上方，点C 的坐标是(-1，0)．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2 倍，记所得的像是△A′B′C．设点B 的对应点B′的横坐标是a，则点B 的横坐标是．➢思考小结1.如图，四边形ABCD 的顶点坐标分别为A(4，2)，B(8，6)，C(6，10)，D(-2，6)．1 A B C D1（）将，，，的横坐标、纵坐标都乘2，得到四个点，以这四个点为顶点的四边形与四边形ABCD 位似吗？如果位似，指出位似中心并求出相似比．（2）将A，B，C，D 的横坐标、纵坐标都乘 1，得到四个2点，以这四个点为顶点的四边形与四边形ABCD 位似吗？如果位似，指出位似中心并求出相似比．（3）在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k（k≠0），所对应的图形与原图形，位似中心是，它们的相似比为．2.实际生活中测量旗杆的高度，都是利用了相似三角形的原理进行的．下列三种方法都利用了物体与地面垂直的特性，除此之外，这三种方法还分别用了哪些实际生活中的原理呢？请把选项填到对应的横线上．①利用阳光下的影子：②利用标杆：③利用镜子的反射：A．镜子的反射定律：借助入射角、反射角相等B．视线与一组平行线相交，同位角相等C．同一时刻，太阳光线（平行光线）与水平地面的夹角相等3.影子上墙问题的常见处理方法：推墙法、砍树法、抬高地面法，这三种方法的实质都是构造三角形相似，在构造的时候，我们主要是想办法构造出来太阳光线与地面的夹角．【参考答案】➢ 巩固练习1. 32. 1003. 7.5 m4. B5. A6. A7. 5.6 m8. 8 m9. (7 + 3) m10. 20 m11. 11.8 m12. 1:213. 614. -3 +a 2➢思考小结1.（1）位似；位似中心是原点；相似比是1 2（2）位似；位似中心是原点；相似比是12（3）位似；原点；|k|．2.C；B；A。

相似三角形应用专题班级： 姓名：1、如图,一名同学(用AB 表示),站在阳光下,通过镜子C 恰好看到旗杆ED 的顶端,已知这名同学的身高是1.60米,他到影子的距离是2米,镜子到旗杆的距离是8米,求旗杆的高.2：如图，零件的外径为16cm ，要求它的壁厚x ，需要先求出内径AB ，现用一个交叉钳(AD 与BC 相等)去量，若测得OA:OD=OB:OC=3:1，CD ＝5cm ，你能求零件的壁厚x 吗？3、为了测量路灯（OS ）的高度,把一根长1.5米的竹竿（AB ）竖直立在水平地面上,测得竹竿的影子（BC ）长为1米,然后拿竹竿向远离路灯方向走了4米（BB ‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B ‘C ‘）为1.8米,求路灯离地面的高度.h S A CB B 'OC 'A '4、晚上，小亮走在大街上，他发现：当他站在大街两边的两盏相同高度的路灯之间，并且自己被两边的路灯罩在地上的影子成一直线时，自己右边的影子长3米，左边影子长为1.5米，如图所示，已知自己身高为1.80米，两盏路灯之间相距12米，求路灯的高度。

5、小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E 处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度 1.2CD =m ，0.8CE =m ，30CA =m （点A E C 、、在同一直线上）． 已知小明的身高EF 是1.7m ，请你帮小明求出楼高AB （结果精确到0.1m ）．6、如图小明想测量电线杆AB 的高度，发现电线杆的影子恰好落在土坡的坡面CD 和地面HGFBC 上，量得CD=4 m ，BC=10 m ，CD 与地面成30°角，且此时测得1 m 杆的影子长为2 m ，则电线杆的高度约为多少米？（结果精确到0.1 m ）7、如图，某测量工作人员与标杆顶端F 、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，求电视塔的高ED 。