新人教版27.2.3相似三角形应用举例(优质课)
- 格式：ppt
- 大小：1.04 MB
- 文档页数：15
下载文档原格式
合集下载
(课件) 27.2.3相似三角形应用举例1
求旗杆高度的方法:
因为旗杆的高度不能直 接测量,我们可以利用
旗杆的高 度和影长 组成的三
角形
人身高和 相似于 影长组成
的三角形
再利用相似三角 形对应边成比例
来求解.
１、旗杆的高度
是线段
；
旗杆的高度与它
的影长组成什么
三角形？（ ）
这个三角形有没
有哪条边可以直
接测量？
Ａ 6m
c
8m
2、人的高度与它的
1、校园里有一棵大树，要测量树的高度， 你有什么方法？
2、在某一时刻，测得一根高为1.8米的竹竿 的影长为3米，同时测得一栋楼的影长为90 米，这栋楼的高度是多少？
3、为了测量一棵树的高度，小林把一小 镜子放在离树（AB）8米的点E处，然后沿 着直线BE后退到点D，这时恰好在镜子里 看到树梢顶点A，再用皮尺量得DE=2.8m， 观察者目高CD=1.6m。这时树高多少？你 能解决这个问题吗？
作业
• 1.课堂作业：课本P43：8、9题； • 2.家庭作业：《配套练习》P37—38页.
人生的价值，并不是用时间，而 是用深度去衡量的。
——列夫·托尔斯泰
学习目标
1.熟练掌握相似三角形的判定和性质； 2.能灵活运用相似三角形的判定和性质
解决实际问题.
相似三角形的判定方法有哪几种？ 1.定义法：对应边成比例，对应角相等的 两个三角形相似。
2.平行法：平行于三角形一边，与另外两边（或两 边的延长线)相交所构成的三角形与三角形相似。
3.(SSS)三边对应成比例的两三角形相似.
4.(SAS)两边成比例且夹角相等的两个三角形相似.
5.(AA)两角对应相等的三角形全等.
6.(HL)斜边和一直角边对应成比例的两三角形全 等.
27.2.3相似三角形的应用举例(2)
点拨：人、标杆和旗杆都垂直于地面．
∵人、标杆和旗杆都垂直于地面， ∴∠ABF＝∠EFD＝∠CDH＝90°， ∴人、标杆和旗杆是互相平行的． ∵EF∥CN，∴∠1＝∠2.
∵∠3＝∠3，△AME∽△ANC，
∴
AM AN
EM CN
.
∵人与标杆的距离、人与旗杆的距离，标杆
与人的身高的差EM都已测量出，
C
D
A
P
Q
B
五、课堂小结
谈谈你在本节课的收获.
六、布置作业
1.必做题： 教材第43-44页习题
3.备选题：
一盗窃犯于夜深人静之时潜入某单位作案，该 单位的自动摄像系统摄下了他作案的全过程.请你为 警方设计一个方案，估计该盗窃犯的大致身高.
∴能求出CN.
∵∠ABF＝∠CDF＝∠AND＝90°，
∴四边形ABND为矩形． ∴DN＝AB. ∴能求出旗杆CD的长度．
8.为了测量路灯（OS）的高度,把一根长1.5米的 竹竿（AB）竖直立在水平地面上,测得竹竿的 影子（BC）长为1米,然后拿竹竿向远离路灯方 向走了4米（BB‘）,再把竹竿竖立在地面上, 测 得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的 高度.
方法一：利用阳光下的影子
操作方法：一名学生在直立于旗杆影子的顶端处, 测出该同学的影长和此时旗杆的影长．
点拨：把太阳的光线看成是平行的.
∵太阳的光线是平行的， ∴AE∥CB，
∴∠AEB＝∠CBD.
∵人与旗杆是垂直于地面的， ∴∠ABE＝∠CDB，
∴△ABE∽△CBD.
∴
AB BE CD BD
.即CD=
S
hA
A'
O BC
B'
C'
∵人、标杆和旗杆都垂直于地面， ∴∠ABF＝∠EFD＝∠CDH＝90°， ∴人、标杆和旗杆是互相平行的． ∵EF∥CN，∴∠1＝∠2.
∵∠3＝∠3，△AME∽△ANC，
∴
AM AN
EM CN
.
∵人与标杆的距离、人与旗杆的距离，标杆
与人的身高的差EM都已测量出，
C
D
A
P
Q
B
五、课堂小结
谈谈你在本节课的收获.
六、布置作业
1.必做题： 教材第43-44页习题
3.备选题：
一盗窃犯于夜深人静之时潜入某单位作案，该 单位的自动摄像系统摄下了他作案的全过程.请你为 警方设计一个方案，估计该盗窃犯的大致身高.
∴能求出CN.
∵∠ABF＝∠CDF＝∠AND＝90°，
∴四边形ABND为矩形． ∴DN＝AB. ∴能求出旗杆CD的长度．
8.为了测量路灯（OS）的高度,把一根长1.5米的 竹竿（AB）竖直立在水平地面上,测得竹竿的 影子（BC）长为1米,然后拿竹竿向远离路灯方 向走了4米（BB‘）,再把竹竿竖立在地面上, 测 得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的 高度.
方法一：利用阳光下的影子
操作方法：一名学生在直立于旗杆影子的顶端处, 测出该同学的影长和此时旗杆的影长．
点拨：把太阳的光线看成是平行的.
∵太阳的光线是平行的， ∴AE∥CB，
∴∠AEB＝∠CBD.
∵人与旗杆是垂直于地面的， ∴∠ABE＝∠CDB，
∴△ABE∽△CBD.
∴
AB BE CD BD
.即CD=
S
hA
A'
O BC
B'
C'
人教版数学九年级下册27.2.3相似三角形的应用举例优秀教学案例
2.引导学生运用相似三角形的性质进行分析和计算，鼓励他们分享解题思路和方法。
3.教师巡回指导，对学生的解题过程进行观察和评价，及时给予指导和鼓励。
4.邀请小组代表分享他们的讨论结果和解题过程，引导其他学生进行学习和借鉴。
（四）总结归纳
1.引导学生回顾本节课所学习的内容，总结相似三角形的性质和应用方法。
1.培养学生对数学学科的兴趣，使他们愿意主动学习数学，提高他们的数学素养。
2.培养学生勇于探究、积极思考的学习精神，使他们养成良好的学习习惯。
3.使学生认识到数学在现实生活中的重要性，培养他们运用数学知识解决实际问题的意识。
4.通过对本节课的学习，使学生感受到数学的乐趣，提高他们的学习积极性。
三、教学策略
2.鼓励学生对自己的学习过程进行评价，发现优点和不足，提高自我认知。
3.组织学生进行互评，让他们在评价中互相学习，共同进步。
4.教师对学生的学习情况进行总结性评价，关注学生的成长和进步，给予肯定和鼓励。
四、教学内容与过程
（一）导入新课
1.利用多媒体展示一幅图片，图片中包含两个相似的三角形，引导学生观察并思考这两个三角形的相似性质。
二、教学目标
（一）知识与技能
1.理解相似三角形的性质，并掌握其在解决实际问题中的应用方法。
2.能够通过具体实例，将实际问题转化为数学问题，并运用相似三角形的性质进行解答。
3.熟练运用相似三角形的性质进行证明和计算，提高解题能力。
4.了解相似三角形在现实生活中的应用，感受数学与生活的紧密联系。
（二）过程与方法
人教版数学九年级下册27.2.3相似三角形的应用举例优秀教学案例
一、案例背景
本节内容是“人教版数学九年级下册27.2.3相似三角形的应用举例”，是在学生已经掌握了相似三角形的性质和判定方法的基础上进行学习的。通过本节课的学习，使学生能够运用相似三角形的性质解决实际问题，提高他们的数学应用能力。
3.教师巡回指导，对学生的解题过程进行观察和评价，及时给予指导和鼓励。
4.邀请小组代表分享他们的讨论结果和解题过程，引导其他学生进行学习和借鉴。
（四）总结归纳
1.引导学生回顾本节课所学习的内容，总结相似三角形的性质和应用方法。
1.培养学生对数学学科的兴趣，使他们愿意主动学习数学，提高他们的数学素养。
2.培养学生勇于探究、积极思考的学习精神，使他们养成良好的学习习惯。
3.使学生认识到数学在现实生活中的重要性，培养他们运用数学知识解决实际问题的意识。
4.通过对本节课的学习，使学生感受到数学的乐趣，提高他们的学习积极性。
三、教学策略
2.鼓励学生对自己的学习过程进行评价，发现优点和不足，提高自我认知。
3.组织学生进行互评，让他们在评价中互相学习，共同进步。
4.教师对学生的学习情况进行总结性评价，关注学生的成长和进步，给予肯定和鼓励。
四、教学内容与过程
（一）导入新课
1.利用多媒体展示一幅图片，图片中包含两个相似的三角形，引导学生观察并思考这两个三角形的相似性质。
二、教学目标
（一）知识与技能
1.理解相似三角形的性质，并掌握其在解决实际问题中的应用方法。
2.能够通过具体实例，将实际问题转化为数学问题，并运用相似三角形的性质进行解答。
3.熟练运用相似三角形的性质进行证明和计算，提高解题能力。
4.了解相似三角形在现实生活中的应用，感受数学与生活的紧密联系。
（二）过程与方法
人教版数学九年级下册27.2.3相似三角形的应用举例优秀教学案例
一、案例背景
本节内容是“人教版数学九年级下册27.2.3相似三角形的应用举例”，是在学生已经掌握了相似三角形的性质和判定方法的基础上进行学习的。通过本节课的学习，使学生能够运用相似三角形的性质解决实际问题，提高他们的数学应用能力。
27.2.3相似三角形应用举例 课件
•这节课我学会（懂得）了…… •这节课我想对师傅（学友）说……
温馨提示：师友交流、总结本节课的知识点、易错点、重难点、解题思路以及蕴含的数学 思想,并互相评价对方的表现,对本节课的互助情况进行总结反思。师傅要对学友今后的努 力方向提出明确的要求。
1. 相似三角形的应用主要有两个方面：
（1） 测高（不能直接使用皮尺或刻度尺量的） 测量不能到达顶部的物体的高度，通常用
操作方法： 1、在观测者和旗杆之间的地面上直立一根高度已知的标杆；
2、观测者前后调整自己的位置，当旗杆顶部、标杆顶
部与眼睛恰好在同一直线上时；
C
3、分别测出她的脚与旗杆底部、标杆底部的距离
，学生眼睛到地面的高度，即可求出旗杆的高度；
怎么办？
E
A 31 M
2
N
B
F
DH
E
A3
1
M
C
2
N
过A作AN⊥CD交EF于M ∵人、标杆和旗杆是互相平行的 ∵EF∥CN
“在同一时刻物高与影长成比例”的原理解决。
（2） 测距（不能直接测量的两点间的距离） 测量不能到达两点间的距离,常构造相似三
角形求解。
利用三角形的相似,可以解决一些不能直接测量 的物体的长度问题,下面请看几个例子。
1、据史料记载,古希腊数学家,天文学家泰勒斯曾利用相 似三角形的原理,在金字塔影子的顶部立一根木杆。借助太阳 光线构成两个相似三角形,来测量金字塔的高度。
必做： 1. 2. 选做：
如图,如果木杆EF长2m,它的影长FD为3m,测OA得为201m, 求金字塔的高度BO。
如图,如果木杆EF长2m,它的影长FD为3m,测OA得为201m,求 金字塔的高度BO。 解:太阳光是平行的光线,因此:∠BAO=∠EDF。 又 ∠AOB=∠DFE=900。
人教版九年级下册数学27.2.3：相似三角形的应用 举例 测量(金字塔高度、河宽)问题 课件 (共12张PPT)
明朝未及，我只有过好每一个今天，唯一的今天。
昨日的明天是今天。明天的昨日是今天。为什么要计较于过去呢（先别急着纠正我的错误，你确实可以在评判过去中学到许多）。但是我发现有的人过分地瞻前顾后了。为 何不想想“现在”呢？为何不及时行乐呢？如果你的回答是“不”，那么是时候该重新考虑一下了。成功的最大障碍是惧怕失败。这些句子都教育我们：不要惧怕失败。如 果你失败了他不会坐下来说：“靠，我真失败，我放弃。”并且不是一个婴儿会如此做，他们都会反反复复，一次一次地尝试。如果一条路走不通，那就走走其他途径，不 断尝试。惧怕失败仅仅是社会导致的一种品质，没有人生来害怕失败，记住这一点。宁愿做事而犯错，也不要为了不犯错而什么都不做。不一定要等到时机完全成熟才动手。 开头也许艰难，但是随着时间的流逝，你会渐渐熟悉你的事业。世上往往没有完美的时机，所以当你觉得做某事还不是时候，先做起来再说吧。喜欢追梦的人，切记不要被 梦想主宰；善于谋划的人，切记空想达不到目标；拥有实干精神的人，切记选对方向比努力做事重要。太阳不会因为你的失意，明天不再升起；月亮不会因为你的抱怨，今 晚不再降落。蒙住自己的眼睛，不等于世界就漆黑一团；蒙住别人的眼睛，不等于光明就属于自己！鱼搅不浑大海，雾压不倒高山，雷声叫不倒山岗，扇子驱不散大雾。鹿 的脖子再长，总高不过它的脑袋。人的脚指头再长，也长不过他的脚板。人的行动再快也快不过思想！以前认为水不可能倒流，那是还没有找到发明抽水机的方法；现在认 为太阳不可能从西边出来，这是还没住到太阳从西边出来的星球上。这个世界只有想不到的，没有做不到的！不是井里没有水，而是挖的不够深；不是成功来的慢，而是放 弃速度快。得到一件东西需要智慧，放弃一样东西则需要勇气！终而复始，日月是也。死而复生，四时是也。奇正相生，循环无端，涨跌相生，循环无端，涨跌相生，循环 无穷。机遇孕育着挑战，挑战中孕育着机遇，这是千古验证了的定律！种子放在水泥地板上会被晒死，种子放在水里会被淹死，种子放到肥沃的土壤里就生根发芽结果。选
昨日的明天是今天。明天的昨日是今天。为什么要计较于过去呢（先别急着纠正我的错误，你确实可以在评判过去中学到许多）。但是我发现有的人过分地瞻前顾后了。为 何不想想“现在”呢？为何不及时行乐呢？如果你的回答是“不”，那么是时候该重新考虑一下了。成功的最大障碍是惧怕失败。这些句子都教育我们：不要惧怕失败。如 果你失败了他不会坐下来说：“靠，我真失败，我放弃。”并且不是一个婴儿会如此做，他们都会反反复复，一次一次地尝试。如果一条路走不通，那就走走其他途径，不 断尝试。惧怕失败仅仅是社会导致的一种品质，没有人生来害怕失败，记住这一点。宁愿做事而犯错，也不要为了不犯错而什么都不做。不一定要等到时机完全成熟才动手。 开头也许艰难，但是随着时间的流逝，你会渐渐熟悉你的事业。世上往往没有完美的时机，所以当你觉得做某事还不是时候，先做起来再说吧。喜欢追梦的人，切记不要被 梦想主宰；善于谋划的人，切记空想达不到目标；拥有实干精神的人，切记选对方向比努力做事重要。太阳不会因为你的失意，明天不再升起；月亮不会因为你的抱怨，今 晚不再降落。蒙住自己的眼睛，不等于世界就漆黑一团；蒙住别人的眼睛，不等于光明就属于自己！鱼搅不浑大海，雾压不倒高山，雷声叫不倒山岗，扇子驱不散大雾。鹿 的脖子再长，总高不过它的脑袋。人的脚指头再长，也长不过他的脚板。人的行动再快也快不过思想！以前认为水不可能倒流，那是还没有找到发明抽水机的方法；现在认 为太阳不可能从西边出来，这是还没住到太阳从西边出来的星球上。这个世界只有想不到的，没有做不到的！不是井里没有水，而是挖的不够深；不是成功来的慢，而是放 弃速度快。得到一件东西需要智慧，放弃一样东西则需要勇气！终而复始，日月是也。死而复生，四时是也。奇正相生，循环无端，涨跌相生，循环无端，涨跌相生，循环 无穷。机遇孕育着挑战，挑战中孕育着机遇，这是千古验证了的定律！种子放在水泥地板上会被晒死，种子放在水里会被淹死，种子放到肥沃的土壤里就生根发芽结果。选
人教版九年级数学下册教案：27.2.3 相似三角形应用举例
2.布置作业：
教材第43页习题27.2第8，9，10题.
通过问题的形式回顾所学基本知识，能够使学生获得整体认知.
【知识网络】
提纲挈领，重点突出.
【教学反思】
①[授课流程反思]
本课时从学生感兴趣的测量金字塔开始，然后测量河宽，最后解决盲区的问题，每一个问题都是抓住怎样把实际问题转化为数学问题这一关键点进行突破.
通过拓展提升使学生加深对实际问题解法的应用，学会并领悟建模思想.
【达标测评】
1.如图27－2－209，为估算学校的旗杆的高度，身高1.6米的张良同学沿着旗杆在地面上的影子AB由点A向点B走去，当他走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC＝2 m，BC＝8 m，则旗杆的高度是(C)
师生活动：教师提出问题，学生理解测量方法.
分析问题：题目的前提是我们只能在河的一边测量河的宽度，所以想到用相似的知识来解决，因此寻找包括河的宽度的相似三角形．分析题目可知△PQR与△PST相似，所以知道QR，ST，QS的长度即可求出PQ的长度.
问题：是否有其他的解题方法？试一试！
师生活动：通过作图可以理解并进行解答.
三：
开放
训练
体现
应用
【应用举例】
例1李明同学为了测量河对岸树AB的高度，他在河岸边放一面平面镜MN，他站在C处通过平面镜看到树的顶端A，如图27－2－207，他量得B，P之间的距离是56米，C，P之间的距离是12米，他的身高是1.74米.图27－2－207
(1)他这种测量方法应用了物理学的什么知识？请简要说明.
2.你能举出现实生活中有哪些相似的例子吗？试一试！
回顾以前所学内容，为学习本节课内容做好准备.
活动
一：
创设
教材第43页习题27.2第8，9，10题.
通过问题的形式回顾所学基本知识，能够使学生获得整体认知.
【知识网络】
提纲挈领，重点突出.
【教学反思】
①[授课流程反思]
本课时从学生感兴趣的测量金字塔开始，然后测量河宽，最后解决盲区的问题，每一个问题都是抓住怎样把实际问题转化为数学问题这一关键点进行突破.
通过拓展提升使学生加深对实际问题解法的应用，学会并领悟建模思想.
【达标测评】
1.如图27－2－209，为估算学校的旗杆的高度，身高1.6米的张良同学沿着旗杆在地面上的影子AB由点A向点B走去，当他走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC＝2 m，BC＝8 m，则旗杆的高度是(C)
师生活动：教师提出问题，学生理解测量方法.
分析问题：题目的前提是我们只能在河的一边测量河的宽度，所以想到用相似的知识来解决，因此寻找包括河的宽度的相似三角形．分析题目可知△PQR与△PST相似，所以知道QR，ST，QS的长度即可求出PQ的长度.
问题：是否有其他的解题方法？试一试！
师生活动：通过作图可以理解并进行解答.
三：
开放
训练
体现
应用
【应用举例】
例1李明同学为了测量河对岸树AB的高度，他在河岸边放一面平面镜MN，他站在C处通过平面镜看到树的顶端A，如图27－2－207，他量得B，P之间的距离是56米，C，P之间的距离是12米，他的身高是1.74米.图27－2－207
(1)他这种测量方法应用了物理学的什么知识？请简要说明.
2.你能举出现实生活中有哪些相似的例子吗？试一试！
回顾以前所学内容，为学习本节课内容做好准备.
活动
一：
创设
27.2.3相似三角形应用举例(优质课)省公开课获奖课件说课比赛一等奖课件
DE BC EF BC
C．AB BC
DE EF
D．DABE
AC DF
例5 如图，为了估算河旳宽度，我们能够在河对岸选定一种目 旳点P，在近岸点Q和S，使点P、Q、S共线且直线PS与河垂直， 接着在过点S且与PS垂直旳直线a上选择合适旳点T，拟定PT与 过点Q且垂直PS旳直线b旳交点R．假如测得QS＝45m，ST＝ 90m，QR＝60m，求河旳宽度PQ．
2. 在处理某些不能直接度量旳物体旳高度或宽
度等测量类问题时，能够借助他物间接测量，这 时往往需要构造相同三角形来处理.
3. 我们把观察者眼睛旳位置称为视点，观察时 ，从下方向上看，视线与水平线旳夹角称为仰角.
4．相同三角形旳实际应用 (1)测量物高 利用“同一时刻旳物高和影长”
比例式为：DABE＝BECF.
FH AH FK CK
为这棵树旳遮挡，右边树 旳顶端点C在观察者旳盲
即 FH 8 1.6 6.4
FH 5 12 1.6 10.4
区之内，观察者看不到 它．
解得 FH＝8
利用相同来处理测量物体高度旳问题旳一般思绪 是怎样旳?
一般情况下，能够从人眼所在旳部位向物体作垂 线，根据人、物体都与地面垂直构造相同三角形 数学模型，利用相同三角形相应边旳比相等处理 问题．
池塘旳宽为36m．
4. 如图是小明设计用手电来测量某古城墙高度旳示 意图，点处放一水平旳平面镜，光线从点出发经 平面镜反射后刚好射到古城墙旳顶端处，已知小
明身高1.6米，且测得BP=2米，PD=10米，那么该
古城墙旳高度是（ B ）
A. 6米 B. 8米 C. 18米 D. 24米
例6 已知左、右并排旳两棵大树旳高分别是AB＝6cm和CD＝ 12m，两树旳根部旳距离BD＝5m．一种身高1.6m旳人沿着正 对这两棵树旳一条水平直路 l 从左向右迈进，当他与左边较低 旳树旳距离不大于多少时，就不能看到右边较高旳树旳顶端点
C．AB BC
DE EF
D．DABE
AC DF
例5 如图，为了估算河旳宽度，我们能够在河对岸选定一种目 旳点P，在近岸点Q和S，使点P、Q、S共线且直线PS与河垂直， 接着在过点S且与PS垂直旳直线a上选择合适旳点T，拟定PT与 过点Q且垂直PS旳直线b旳交点R．假如测得QS＝45m，ST＝ 90m，QR＝60m，求河旳宽度PQ．
2. 在处理某些不能直接度量旳物体旳高度或宽
度等测量类问题时，能够借助他物间接测量，这 时往往需要构造相同三角形来处理.
3. 我们把观察者眼睛旳位置称为视点，观察时 ，从下方向上看，视线与水平线旳夹角称为仰角.
4．相同三角形旳实际应用 (1)测量物高 利用“同一时刻旳物高和影长”
比例式为：DABE＝BECF.
FH AH FK CK
为这棵树旳遮挡，右边树 旳顶端点C在观察者旳盲
即 FH 8 1.6 6.4
FH 5 12 1.6 10.4
区之内，观察者看不到 它．
解得 FH＝8
利用相同来处理测量物体高度旳问题旳一般思绪 是怎样旳?
一般情况下，能够从人眼所在旳部位向物体作垂 线，根据人、物体都与地面垂直构造相同三角形 数学模型，利用相同三角形相应边旳比相等处理 问题．
池塘旳宽为36m．
4. 如图是小明设计用手电来测量某古城墙高度旳示 意图，点处放一水平旳平面镜，光线从点出发经 平面镜反射后刚好射到古城墙旳顶端处，已知小
明身高1.6米，且测得BP=2米，PD=10米，那么该
古城墙旳高度是（ B ）
A. 6米 B. 8米 C. 18米 D. 24米
例6 已知左、右并排旳两棵大树旳高分别是AB＝6cm和CD＝ 12m，两树旳根部旳距离BD＝5m．一种身高1.6m旳人沿着正 对这两棵树旳一条水平直路 l 从左向右迈进，当他与左边较低 旳树旳距离不大于多少时，就不能看到右边较高旳树旳顶端点
新人教版27.2.3相似三角形应用举例(优质课)
设观察者眼晴的位置（视点） 为F，∠CFK和∠AFH分别是 观察点C、A的仰角，区域Ⅰ 和区域Ⅱ都在观察者看不到 的区域（盲区）之内。 WXQ
解：假设观察者从左向右走到点E时，他的眼睛的 位置点F与两棵树的顶端点A、C在一条直线上。 ∵AB⊥L，CD⊥L， ∴AB∥CD，△AFH∽△CFK， FH AH ∴ FK CK 即 FH 8 1 .6 ，
A(F)
B E 2m O 201m 3m D
A(F)
解：太阳光是平行线， 因此∠BAO= ∠EDF
又 ∠AOB= ∠DFE=90° ∴△ABO∽△DEF BO OA = EF FD OA· EF 201×2 BO = = = 134 FD 3
1.小华为了测量所住楼房的高度，他请来同学 帮忙，测量了同一时刻他自己的影长和楼房的 影长分别是0.5米和15米．已知小华的身高为 1.6米，那么他所住楼房的高度为 米．
BD EC 120 50 解得AB 100(米) DC 60 WXQ 答： 两岸间的大致距离为 100米．
一题多解
我们还可以在河对岸选定一目标点A，再在河的一边选 点D和 E，使DE⊥AD，然后，再选点B，作BC∥DE， 与视线EA相交于点C。此时，测得DE , BC, BD, 就可 以求两岸间的大致距离AB了。
27.2.2 相似三角形应用举例
复习回顾 1、判断两三角形相似有哪些方法?
定义，平行法，(SSS)，(SAS)，(AA)，(HL)
2、相似三角形有什么性质？
（1）对应边的比相等，对应角相等 （2）相似三角形的周长比等于相似比 （3）相似三角形的面积比等于相似比的平方 （4）相似三角形的对应边上的高、中线、角 平分线的长度比等于相似比
复习回顾
人教版数学相似三角形应用举例ppt优质课件3
长FD为3m,测得OA为201m,求金
如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
字塔的高度BO. 方法4：两边对应成比例且夹角相等.
（2）对应线段的比等于相似比（对应中线的比、对应高 经测量，地面部分影长BC为6. 5m时,长臂端点升高 m。 方法6：斜边直角边对应成比例. 例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T, 确定PT与过点Q且垂直PS的直线b的交点为R. 8米 C. 3相似三角形应用举例(1) 2、相似三角形的性质： 8米 C. 解：∵∠PQR=∠PST=90°，∠P=∠P 方法2:（平行法）平行于三角形一边的直线和其它两边相交 ， （2）对应线段的比等于相似比（对应中线的比、对应高 8m的竹竿的影长为3m，同时测得一栋高楼的影长为90m，这栋高楼的高度是 m. 据史料记载,古希腊数学家,天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆. 例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T, 确定PT与过点Q且垂直PS的直线b的交点为R. 方法2:（平行法）平行于三角形一边的直线和其它两边相交 ， 4米，墙上影长CD为1. （3）周长的比等于相似比. 他在某一时刻测得小树EF高为1. 2、相似三角形的性质：
如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
8m的竹竿的影长为3m，同时测得一栋高楼的影长为90m，这栋高楼的高度是 m.
例2、如图,为了估算河的宽度,我们可以在河对岸选P定一个目标点P,在河的这一边取N点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,
如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
字塔的高度BO. 方法4：两边对应成比例且夹角相等.
（2）对应线段的比等于相似比（对应中线的比、对应高 经测量，地面部分影长BC为6. 5m时,长臂端点升高 m。 方法6：斜边直角边对应成比例. 例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T, 确定PT与过点Q且垂直PS的直线b的交点为R. 8米 C. 3相似三角形应用举例(1) 2、相似三角形的性质： 8米 C. 解：∵∠PQR=∠PST=90°，∠P=∠P 方法2:（平行法）平行于三角形一边的直线和其它两边相交 ， （2）对应线段的比等于相似比（对应中线的比、对应高 8m的竹竿的影长为3m，同时测得一栋高楼的影长为90m，这栋高楼的高度是 m. 据史料记载,古希腊数学家,天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆. 例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T, 确定PT与过点Q且垂直PS的直线b的交点为R. 方法2:（平行法）平行于三角形一边的直线和其它两边相交 ， 4米，墙上影长CD为1. （3）周长的比等于相似比. 他在某一时刻测得小树EF高为1. 2、相似三角形的性质：
如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
8m的竹竿的影长为3m，同时测得一栋高楼的影长为90m，这栋高楼的高度是 m.
例2、如图,为了估算河的宽度,我们可以在河对岸选P定一个目标点P,在河的这一边取N点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,
《27.2.3 相似三角形的应用举例》教案、导学案、同步练习
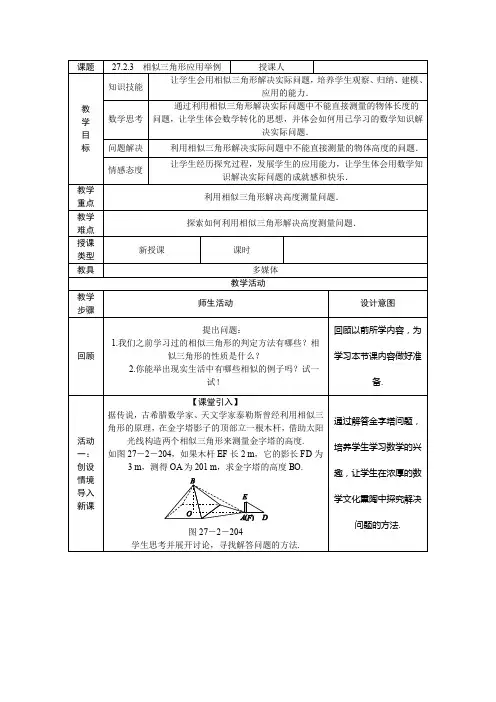
27.2.3 相似三角形的应用举例【教学目标】1．运用三角形相似的知识计算不能直接测量物体的长度和高度；(重点) 2．灵活运用三角形相似的知识解决实际问题．(难点)【教学过程】一、情境导入胡夫金字塔是埃及现存规模最大的金字塔，被喻为“世界古代七大奇观之一” .在古希腊，有一位伟大的科学家叫泰勒斯．一天，希腊国王阿马西斯对他说：“听说你什么都知道，那就请你测量一下埃及金字塔的高度吧！”这在当时条件下是个大难题，因为是很难爬到塔顶的．你知道泰勒斯是怎样测量金字塔的高度的吗？二、合作探究探究点：相似三角形的应用【类型一】利用影子的长度测量物体的高度如图，某一时刻一根2m长的竹竿EF的影长GE为1.2m，此时，小红测得一棵被风吹斜的柏树与地面成30°角，树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6m，求树AB的长．解析：先利用△BDC∽△FGE得到BC3.6＝21.2，可计算出BC＝6m，然后在Rt△ABC中利用含30度的直角三角形三边的关系即可得到AB的长．解：如图，CD＝3.6m，∵△BDC∽△FGE，∴BCCD＝EFGE，即BC3.6＝21.2，∴BC＝6m.在Rt△ABC中，∵∠A＝30°，∴AB＝2BC＝12m，即树长AB是12m.方法总结：解答此类问题时，首先要把实际问题转化为数学问题．利用相似三角形对应边成比例建立相等关系求解．【类型二】利用镜子的反射测量物体的高度小红用下面的方法来测量学校教学大楼AB的高度．如图，在水平地面点E处放一面平面镜，镜子与教学大楼的距离AE＝20m.当她与镜子的距离CE＝2.5m时，她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC ＝1.6m，请你帮助小红测量出大楼AB的高度(注：入射角＝反射角)．解析：根据物理知识得到∠BEA＝∠DEC，所以可得△BAE∽△DCE，再根据相似三角形的性质解答．解：如图，∵根据光的反射定律知∠BEA＝∠DEC，∵∠BAE＝∠DCE＝90°，∴△BAE∽△DCE，∴ABDC＝AEEC.∵CE＝2.5m，DC＝1.6m，∴AB1.6＝202.5，∴AB＝12.8，∴大楼AB的高度为12.8m.方法总结：解本题的关键是找出相似的三角形，然后根据对应边成比例列出方程．解题时要灵活运用所学各学科知识．【类型三】利用标杆测量物体的高度如图，某一时刻，旗杆AB影子的一部分在地面上，另一部分在建筑物的墙面上．小明测得旗杆AB在地面上的影长BC为9.6m，在墙面上的影长CD为2m.同一时刻，小明又测得竖立于地面长1m的标杆的影长为1.2m.请帮助小明求出旗杆的高度．解析：根据在同一时刻物高与影长成正比例，利用相似三角形的对应边成比例解答即可．解：如图，过点D作DE∥BC，交AB于E，∴DE＝CB＝9.6m，BE＝CD＝2m，∵在同一时刻物高与影长成正比例，∴EA∶ED＝1∶1.2，∴AE＝8m，∴AB＝AE＋EB＝8＋2＝10m，∴学校旗杆的高度为10m.方法总结：利用杆或直尺测量物体的高度就是利用杆(或直尺)的高(长)作为三角形的边构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．【类型四】利用相似三角形的性质设计方案测量高度星期天，小丽和同学们在碧沙岗公园游玩，他们来到1928年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前，小丽问：“这个纪念碑有多高呢？”请你利用初中数学知识，设计一种方案测量纪念碑的高度(画出示意图)，并说明理由．解析：设计相似三角形，利用相似三角形的性质求解即可．在距离纪念碑AB的地面上平放一面镜子E，人退后到D处，在镜子里恰好看见纪念碑顶A.若人眼距地面距离为CD，测量出CD、DE、BE的长，就可算出纪念碑AB的高．解：设计方案例子：如图，在距离纪念碑AB的地面上平放一面镜子E，人退后到D处，在镜子里恰好看见纪念碑顶A.若人眼距地面距离为CD，测量出CD、DE、BE的长，就可算出纪念碑AB的高．理由：测量出CD、DE、BE的长，因为∠CED＝∠AEB，∠D＝∠B＝90°，易得△ABE∽△CDE.根据CDAB＝DEBE，即可算出AB的高．方法总结：解题的关键是根据相似三角形的性质设计出具体图形，将实际问题抽象出数学问题求解．三、板书设计1．利用相似三角形测量物体的高度；2．利用相似三角形测量河的宽度；3．设计方案测量物体高度．【教学反思】通过本节知识的学习，可以使学生综合运用三角形相似的判定和性质解决问题，发展学生的应用意识，加深学生对相似三角形的理解和认识．基本达到了预期的教学目标，大部分学生都学会了建立数学模型，利用相似的判定和性质来解决实际问题.27.2.3 相似三角形的应用举例〔学习设计〕，即，， 。
《相似三角形应用举例》优质课一等奖教学设计
相似三角形应用举例【教学目标】1.进一步稳固相似三角形的知识。
2.能够运用三角形相似的知识，解决不能直接测量物体的长度和高度〔如测量金字塔高度问题、测量河宽问题、盲区问题〕等的一些实际问题。
3.通过把实际问题转化成有关相似三角形的数学模型，进一步了解数学建模的思想，培养分析问题、解决问题的能力。
【教学重难点】1．重点：运用三角形相似的知识计算不能直接测量物体的长度和高度。
2．难点：灵活运用三角形相似的知识解决实际问题〔如何把实际问题抽象为数学问题〕。
【教学过程】难点的突破方法〔1〕本节主要探索的是应用相似三角形的判定、性质等知识去解决某些简单的实际问题〔计算不能直接测量物体的长度和高度及盲区问题〕，学生已经学过了相似三角形的概念、判定方法及性质，在此根底上通过本课的学习将对前面所学知识进展全面应用。
初三学生在思维上已具备了初步的应用数学的意识，在心理特点上那么更依赖于直观形象的认识。
〔2〕在实际生活中，面对不能直接测量出长度和宽度的物体及盲区问题，我们可以应用相似三角形的知识来测量，只要将实际问题转化为数学问题，建立相似三角形模型，再利用线段成比例来求解。
在教学中，要通过这些知识的教学，帮助学生从实际生活中发现数学问题、运用所学知识解决实际问题。
另外，还可以根据学生实情，选择一些实际问题，引导学生加以解决，提高他们应用知识解决问题的能力。
〔3〕课上可以通过著名的科学家名句和如何测量神秘的金字塔的高度来激发学生学数学的兴趣，使学生积极参与探索，体验成功的喜悦。
〔4〕运用三角形相似的知识解决实际问题对于学生来说难度较大，可以适当增加课时。
例题的意图相似三角形的应用主要有如下两个方面：〔1〕测高(不能直接使用皮尺或刻度尺量的)；〔2〕测距(不能直接测量的两点间的距离) 。
本节课通过例题的讲解，使学生掌握测高和测距的方法。
知道在实际测量物体的高度、宽度时，关键是要构造和实物所在三角形相似的三角形，而且要能测量三角形的各条线段的长，运用相似三角形的性质列出比例式求解。
27.2.3相似三角形应用举例课件(共33张PPT)(共33张PPT)
A
B
D
C
E
如图:为了估算河的宽度,我们可以在河对岸
选定一个目标作为点A,再在河的这一边选点B和C,
使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC
和AE的交点D.此时如果测得BD=120米,DC=60
米,EC=50米,求两岸间的大致距离AB.
解: ∵ ∠ ADB = ∠ EDC
A
∠ ABC =∠ECD =900.
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
温馨提示：
１、旗杆的高度是线
段 BC ；旗杆的高
度与它的影长组成什
么三角R形t△？ABC
（
）这个三
角形有没有哪条边可
以直接测量？
Ａ
6m
P
Q Rb
a
S
T
知பைடு நூலகம்要点
测距的方法 测量不能到达两点间的距离,常构造 相似三角形求解。
如图:为了估算河的宽度,我们可以
在河对岸选定一个目标作为点A,再在河的 这一边选点B和C,使AB⊥BC,然后,再选点E, 使EC⊥BC,用视线确定BC和AE的交点D.此 时如果测得BD=120米,DC=60米,EC=50米, 求两岸间的大致距离AB.
毫米。 因为PN∥BC，所以△APN∽ △ABC
PE N
所以
AE
PN =
AD
BC
B Q DM C
因此
80–x =
x
，得 x=48（毫米）。答：-------。
80
120
课堂小结
一 、相似三角形的应用主要有如下两个方面
B
D
C
E
如图:为了估算河的宽度,我们可以在河对岸
选定一个目标作为点A,再在河的这一边选点B和C,
使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC
和AE的交点D.此时如果测得BD=120米,DC=60
米,EC=50米,求两岸间的大致距离AB.
解: ∵ ∠ ADB = ∠ EDC
A
∠ ABC =∠ECD =900.
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
温馨提示：
１、旗杆的高度是线
段 BC ；旗杆的高
度与它的影长组成什
么三角R形t△？ABC
（
）这个三
角形有没有哪条边可
以直接测量？
Ａ
6m
P
Q Rb
a
S
T
知பைடு நூலகம்要点
测距的方法 测量不能到达两点间的距离,常构造 相似三角形求解。
如图:为了估算河的宽度,我们可以
在河对岸选定一个目标作为点A,再在河的 这一边选点B和C,使AB⊥BC,然后,再选点E, 使EC⊥BC,用视线确定BC和AE的交点D.此 时如果测得BD=120米,DC=60米,EC=50米, 求两岸间的大致距离AB.
毫米。 因为PN∥BC，所以△APN∽ △ABC
PE N
所以
AE
PN =
AD
BC
B Q DM C
因此
80–x =
x
，得 x=48（毫米）。答：-------。
80
120
课堂小结
一 、相似三角形的应用主要有如下两个方面
27.2.3相似三角形应用举例PPT课件
又∵∠ABO＝∠A′B′O′＝90°， ∴△OAB∽△O′A′B′. ∴OB∶O′B′＝AB∶A′B′.
∴OB＝ ABOB 2741 137
AB
2
答:金字塔高为137米．
（米）
例2. 在△ABC中，AC=4,AB=5，D是AC 上一动点,且∠ADE=∠B,设AD=x,AE=y,试 写出y与x之间的函数关系式，并画出函数 的图像.
一、回顾与复习
（一）相似三角形的判定
1.两角 对应相等 的两个三角形相似. 2.两边 对应成比例且夹角 相等的两个三角形相似. 3.三边 对应成比例的两个三角形相似.
（二）相似三角形的性质
1.对应角 相等，对应边 成比例. 2.对应高 的比，对应中线 的比，对应角平分线 的 比都等于相似比.（相似形中的对应线段） 3.周长的比等于相似比 . 4.面积的比 等于相似比的平方 .
二、探索与应用
例1. 如图所示，为了测量金字塔的高度OB，先竖 一根已知长度的木棒O′B′，比较棒子的影长A′B′ 与金字塔的影长AB，即可近似算出金字塔的高度 OB．如果O′B′＝1m，A′B′＝2m，AB＝274m， 求金字塔的高度OB.
解：∵太阳光是平行光线， ∴∠OAB＝∠O′A′B′．
三、思考与演练
1、 在△ABC中，BC=a，DE∥BC，交
AB于E，交AC于D，SADE S梯形BCDE
求DE的长度.
A
E
D
B
C
A
D
2.已知:四边形ABCD
中,AC平分∠BCD,
∠D= ∠BAC.、布置作业
课本58页第11----12题
∴OB＝ ABOB 2741 137
AB
2
答:金字塔高为137米．
（米）
例2. 在△ABC中，AC=4,AB=5，D是AC 上一动点,且∠ADE=∠B,设AD=x,AE=y,试 写出y与x之间的函数关系式，并画出函数 的图像.
一、回顾与复习
（一）相似三角形的判定
1.两角 对应相等 的两个三角形相似. 2.两边 对应成比例且夹角 相等的两个三角形相似. 3.三边 对应成比例的两个三角形相似.
（二）相似三角形的性质
1.对应角 相等，对应边 成比例. 2.对应高 的比，对应中线 的比，对应角平分线 的 比都等于相似比.（相似形中的对应线段） 3.周长的比等于相似比 . 4.面积的比 等于相似比的平方 .
二、探索与应用
例1. 如图所示，为了测量金字塔的高度OB，先竖 一根已知长度的木棒O′B′，比较棒子的影长A′B′ 与金字塔的影长AB，即可近似算出金字塔的高度 OB．如果O′B′＝1m，A′B′＝2m，AB＝274m， 求金字塔的高度OB.
解：∵太阳光是平行光线， ∴∠OAB＝∠O′A′B′．
三、思考与演练
1、 在△ABC中，BC=a，DE∥BC，交
AB于E，交AC于D，SADE S梯形BCDE
求DE的长度.
A
E
D
B
C
A
D
2.已知:四边形ABCD
中,AC平分∠BCD,
∠D= ∠BAC.、布置作业
课本58页第11----12题
人教版九年级数学下册27.2.3相似三角形应用举例说课稿
3.引发思考：鼓励学生尝试用自己的语言描述相似三角形的特征，为新课的学习做好铺垫。
（二）新知讲授
在新知讲授阶段，我将按照以下步骤逐步呈现知识点，引导学生深入理解：
1.概念阐述：明确相似三角形的定义，解释其与全等三角形的区别与联系。
2.性质分析：通过示例和证明，引导学生发现并理解相似三角形的性质。
3.判定方法：介绍并解释相似三角形的判定方法，如AA、SSS、SAS等，结合具体实例进行分析。
本节课的主要知识点有：
1.相似三角形的性质及其证明；
2.相似三角形的判定方法；
3.相似三角形在实际问题中的应用。
（二）教学目标
知识与技能：
1.掌握相似三角形的性质及其证明；
2.熟练运用相似三角形的判定方法；
3.能够运用相似三角形解决实际问题。
过程与方法：
1.通过实际问题的引入，培养学生从问题中抽象出数学模型的能力；
在本节课中，我将使用以下教具、多媒体资源和技术工具：
1.教具：三角板、量角器等，用于直观展示相似三角形的性质和判定方法；
2.多媒体资源：PPT、教学视频等，展示实际问题和解题过程，帮助学生更好地理解和掌握知识；
3.技术工具：交互式电子白板，实现师生互动、生生互动，提高课堂参与度。
（三）互动方式
为了促进学生的参与和合作，我计划设计以下师生互动和生生互动环节：
四、教学过程设计
（一）导入新课
为了快速吸引学生的注意力和兴趣，我将采用以下方式导入新课：
1.创设情境：通过展示实际生活中相似三角形的例子，如建筑物的立面图、摄影中的构图等，让学生感受到相似三角形在生活中的广泛应用。
2.提出问题：以情境为背景，提出与相似三角形相关的问题，如“为什么这些图形看起来如此和谐？”、“它们之间有什么联系？”等，激发学生的好奇心和求知欲。
（二）新知讲授
在新知讲授阶段，我将按照以下步骤逐步呈现知识点，引导学生深入理解：
1.概念阐述：明确相似三角形的定义，解释其与全等三角形的区别与联系。
2.性质分析：通过示例和证明，引导学生发现并理解相似三角形的性质。
3.判定方法：介绍并解释相似三角形的判定方法，如AA、SSS、SAS等，结合具体实例进行分析。
本节课的主要知识点有：
1.相似三角形的性质及其证明；
2.相似三角形的判定方法；
3.相似三角形在实际问题中的应用。
（二）教学目标
知识与技能：
1.掌握相似三角形的性质及其证明；
2.熟练运用相似三角形的判定方法；
3.能够运用相似三角形解决实际问题。
过程与方法：
1.通过实际问题的引入，培养学生从问题中抽象出数学模型的能力；
在本节课中，我将使用以下教具、多媒体资源和技术工具：
1.教具：三角板、量角器等，用于直观展示相似三角形的性质和判定方法；
2.多媒体资源：PPT、教学视频等，展示实际问题和解题过程，帮助学生更好地理解和掌握知识；
3.技术工具：交互式电子白板，实现师生互动、生生互动，提高课堂参与度。
（三）互动方式
为了促进学生的参与和合作，我计划设计以下师生互动和生生互动环节：
四、教学过程设计
（一）导入新课
为了快速吸引学生的注意力和兴趣，我将采用以下方式导入新课：
1.创设情境：通过展示实际生活中相似三角形的例子，如建筑物的立面图、摄影中的构图等，让学生感受到相似三角形在生活中的广泛应用。
2.提出问题：以情境为背景，提出与相似三角形相关的问题，如“为什么这些图形看起来如此和谐？”、“它们之间有什么联系？”等，激发学生的好奇心和求知欲。
27.2.3相似三角形的应用举例教案
27.2.3 相似三角形的应用举例1．运用三角形相似的知识计算不能直接测量物体的长度和高度；(重点)2．灵活运用三角形相似的知识解决实际问题．(难点)一、情境导入胡夫金字塔是埃及现存规模最大的金字塔，被喻为“世界古代七大奇观之一” .在古希腊，有一位伟大的科学家叫泰勒斯．一天，希腊国王阿马西斯对他说：“听说你什么都知道，那就请你测量一下埃及金字塔的高度吧！”这在当时条件下是个大难题，因为是很难爬到塔顶的．你知道泰勒斯是怎样测量金字塔的高度的吗？二、合作探究探究点：相似三角形的应用【类型一】 利用影子的长度测量物体的高度如图，某一时刻一根2m 长的竹竿EF 的影长GE 为1.2m ，此时，小红测得一棵被风吹斜的柏树与地面成30°角，树顶端B 在地面上的影子点D 与B 到垂直地面的落点C 的距离是3.6m ，求树AB 的长．解析：先利用△BDC ∽△FGE 得到BC 3.6＝21.2，可计算出BC ＝6m ，然后在Rt △ABC 中利用含30度的直角三角形三边的关系即可得到AB 的长．解：如图，CD ＝3.6m ，∵△BDC ∽△FGE ，∴BC CD ＝EF GE ，即BC 3.6＝21.2，∴BC ＝6m.在Rt △ABC 中，∵∠A ＝30°，∴AB ＝2BC ＝12m ，即树长AB 是12m.方法总结：解答此类问题时，首先要把实际问题转化为数学问题．利用相似三角形对应边成比例建立相等关系求解．变式训练：见《学练优》本课时练习“课堂达标训练” 第1题【类型二】 利用镜子的反射测量物体的高度小红用下面的方法来测量学校教学大楼AB 的高度．如图，在水平地面点E 处放一面平面镜，镜子与教学大楼的距离AE ＝20m.当她与镜子的距离CE ＝2.5m 时，她刚好能从镜子中看到教学大楼的顶端B .已知她的眼睛距地面高度DC ＝1.6m ，请你帮助小红测量出大楼AB 的高度(注：入射角＝反射角)．解析：根据物理知识得到∠BEA ＝∠DEC ，所以可得△BAE ∽△DCE ，再根据相似三角形的性质解答．解：如图，∵根据光的反射定律知∠BEA ＝∠DEC ，∵∠BAE ＝∠DCE ＝90°，∴△BAE∽△DCE ，∴AB DC ＝AE EC .∵CE ＝2.5m ，DC ＝1.6m ，∴AB 1.6＝202.5，∴AB ＝12.8，∴大楼AB 的高度为12.8m.方法总结：解本题的关键是找出相似的三角形，然后根据对应边成比例列出方程．解题时要灵活运用所学各学科知识．变式训练：见《学练优》本课时练习“课堂达标训练” 第5题【类型三】 利用标杆测量物体的高度如图，某一时刻，旗杆AB 影子的一部分在地面上，另一部分在建筑物的墙面上．小明测得旗杆AB 在地面上的影长BC 为9.6m ，在墙面上的影长CD 为2m.同一时刻，小明又测得竖立于地面长1m 的标杆的影长为1.2m.请帮助小明求出旗杆的高度．解析：根据在同一时刻物高与影长成正比例，利用相似三角形的对应边成比例解答即可． 解：如图，过点D 作DE ∥BC ，交AB 于E ，∴DE ＝CB ＝9.6m ，BE ＝CD ＝2m ，∵在同一时刻物高与影长成正比例，∴EA ∶ED ＝1∶1.2，∴AE ＝8m ，∴AB ＝AE ＋EB ＝8＋2＝10m ，∴学校旗杆的高度为10m.方法总结：利用杆或直尺测量物体的高度就是利用杆(或直尺)的高(长)作为三角形的边构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．变式训练：见《学练优》本课时练习“课堂达标训练”第3题【类型四】 利用相似三角形的性质设计方案测量高度星期天，小丽和同学们在碧沙岗公园游玩，他们来到1928年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前，小丽问：“这个纪念碑有多高呢？”请你利用初中数学知识，设计一种方案测量纪念碑的高度(画出示意图)，并说明理由．解析：设计相似三角形，利用相似三角形的性质求解即可．在距离纪念碑AB 的地面上平放一面镜子E ，人退后到D 处，在镜子里恰好看见纪念碑顶A .若人眼距地面距离为CD ，测量出CD 、DE 、BE 的长，就可算出纪念碑AB 的高．解：设计方案例子：如图，在距离纪念碑AB 的地面上平放一面镜子E ，人退后到D 处，在镜子里恰好看见纪念碑顶A .若人眼距地面距离为CD ，测量出CD 、DE 、BE 的长，就可算出纪念碑AB 的高．理由：测量出CD 、DE 、BE 的长，因为∠CED ＝∠AEB ，∠D ＝∠B ＝90°，易得△ABE ∽△CDE .根据CD AB ＝DE BE，即可算出AB 的高．方法总结：解题的关键是根据相似三角形的性质设计出具体图形，将实际问题抽象出数学问题求解．变式训练：见《学练优》本课时练习“课后巩固提升”第6题三、板书设计1．利用相似三角形测量物体的高度；2．利用相似三角形测量河的宽度；3．设计方案测量物体高度．通过本节知识的学习，可以使学生综合运用三角形相似的判定和性质解决问题，发展学生的应用意识，加深学生对相似三角形的理解和认识．基本达到了预期的教学目标，大部分学生都学会了建立数学模型，利用相似的判定和性质来解决实际问题.。
人教版九年级数学下27.2相似三角形小结优秀教学案例
（一）导入新课
1.利用生活情境，引发学生兴趣。
在导入新课时，我会利用与生活相关的情境，引发学生的学习兴趣。例如，我可以展示一些建筑设计图，让学生观察并思考：如何在设计中利用相似三角形的性质？这样既能激发学生的学习兴趣，又能引导学生思考相似三角形在实际生活中的应用。
2.回已有知识，为新课学习做好铺垫。
（五）作业小结
1.设计具有针对性的作业，巩固所学知识。
在布置作业时，我会设计一些具有针对性的题目，让学生通过完成作业，巩固所学知识。例如，我可以设计一些关于相似三角形的判定和性质的练习题，让学生在完成作业的过程中，加深对知识的理解和运用。
2.鼓励学生进行自我反思，提高自我监控能力。
在布置作业时，我会鼓励学生进行自我反思，让学生思考自己在学习过程中的优点和不足，从而提高学生的自我监控能力。例如，我可以让学生在作业中总结自己在学习相似三角形时的思维方式和方法，以及遇到的困难和解决方法。
2.培养学生运用数学知识解决实际问题的能力，提高学生的创新思维。
在教学过程中，我会以一个实际问题为背景，让学生分组讨论，探讨相似三角形在实际问题中的应用，培养学生的合作意识和解决问题的能力。同时，我会鼓励学生提出问题，引导他们通过讨论、思考解决问题，从而提高学生的思维能力和创新能力。
（二）过程与方法
在教学过程中，我会引导学生分工合作，完成一些具有挑战性的任务。例如，在讲解相似三角形的判定时，我可以让学生分组进行实验，通过实际操作验证相似三角形的性质，从而提高学生的团队协作能力。
（四）反思与评价
1.引导学生进行自我反思，提高学生的自我监控能力。
在教学过程中，我会引导学生进行自我反思，让学生思考自己在学习过程中的优点和不足，从而提高学生的自我监控能力。例如，在讲解相似三角形的性质时，我可以让学生回顾自己的学习过程，思考自己在解决问题时的思维方式和方法。
1.利用生活情境，引发学生兴趣。
在导入新课时，我会利用与生活相关的情境，引发学生的学习兴趣。例如，我可以展示一些建筑设计图，让学生观察并思考：如何在设计中利用相似三角形的性质？这样既能激发学生的学习兴趣，又能引导学生思考相似三角形在实际生活中的应用。
2.回已有知识，为新课学习做好铺垫。
（五）作业小结
1.设计具有针对性的作业，巩固所学知识。
在布置作业时，我会设计一些具有针对性的题目，让学生通过完成作业，巩固所学知识。例如，我可以设计一些关于相似三角形的判定和性质的练习题，让学生在完成作业的过程中，加深对知识的理解和运用。
2.鼓励学生进行自我反思，提高自我监控能力。
在布置作业时，我会鼓励学生进行自我反思，让学生思考自己在学习过程中的优点和不足，从而提高学生的自我监控能力。例如，我可以让学生在作业中总结自己在学习相似三角形时的思维方式和方法，以及遇到的困难和解决方法。
2.培养学生运用数学知识解决实际问题的能力，提高学生的创新思维。
在教学过程中，我会以一个实际问题为背景，让学生分组讨论，探讨相似三角形在实际问题中的应用，培养学生的合作意识和解决问题的能力。同时，我会鼓励学生提出问题，引导他们通过讨论、思考解决问题，从而提高学生的思维能力和创新能力。
（二）过程与方法
在教学过程中，我会引导学生分工合作，完成一些具有挑战性的任务。例如，在讲解相似三角形的判定时，我可以让学生分组进行实验，通过实际操作验证相似三角形的性质，从而提高学生的团队协作能力。
（四）反思与评价
1.引导学生进行自我反思，提高学生的自我监控能力。
在教学过程中，我会引导学生进行自我反思，让学生思考自己在学习过程中的优点和不足，从而提高学生的自我监控能力。例如，在讲解相似三角形的性质时，我可以让学生回顾自己的学习过程，思考自己在解决问题时的思维方式和方法。
人教版数学九年级下册27.2.3相似三角形应用举例(教案)
五、教学反思
今天在讲解相似三角形应用举例的过程中，我发现学生们对于理论知识的学习相对扎实，能够跟上课程的节奏。但在实际问题的应用上，部分学生还是显得有些吃力。我意识到，将抽象的数学概念与生活实际相结合，并非易事。
在讲授新课的过程中，我尽量用生动的语言和例子来解释相似三角形的应用，希望能够激发学生的兴趣。通过案例分析，他们对于相似三角形在实际生活中的运用有了更直观的认识。然而，我也注意到，有些学生在将理论知识运用到具体问题时，还是显得有些力不从心。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了相似三角形的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对相似三角形应用的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
3.通过具体例子，让学生掌握以下相似三角形应用方法：
-利用相似三角形对应边成比例求解未知长度。
-利用相似三角形对应角相等判断形状。
-解决实际问题中涉及的相似三角形问题，如高度、距离等测量。
本节课将结合课本例题和习题，使学生在实际操作中掌握相似三角形的应用。
二、核心素养目标
1.培养学生运用数学知识解决实际问题的能力，特别是利用相似三角形性质进行问题分析和解决。
人教版数学九年级下册27.2.3相似三角形应用举例（教案）
一、教学内容
人教版数学九年级下册27.2.3相似三角形应用举例。本节课主要内容包括：
1.探索并理解相似三角形在现实生活中的应用，如测量物体长度、距离等。
2.学会运用相似三角形的性质解决实际问题，包括直角三角形、等腰三角形以及一般三角形的相似问题。
今天在讲解相似三角形应用举例的过程中，我发现学生们对于理论知识的学习相对扎实，能够跟上课程的节奏。但在实际问题的应用上，部分学生还是显得有些吃力。我意识到，将抽象的数学概念与生活实际相结合，并非易事。
在讲授新课的过程中，我尽量用生动的语言和例子来解释相似三角形的应用，希望能够激发学生的兴趣。通过案例分析，他们对于相似三角形在实际生活中的运用有了更直观的认识。然而，我也注意到，有些学生在将理论知识运用到具体问题时，还是显得有些力不从心。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了相似三角形的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对相似三角形应用的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
3.通过具体例子，让学生掌握以下相似三角形应用方法：
-利用相似三角形对应边成比例求解未知长度。
-利用相似三角形对应角相等判断形状。
-解决实际问题中涉及的相似三角形问题，如高度、距离等测量。
本节课将结合课本例题和习题，使学生在实际操作中掌握相似三角形的应用。
二、核心素养目标
1.培养学生运用数学知识解决实际问题的能力，特别是利用相似三角形性质进行问题分析和解决。
人教版数学九年级下册27.2.3相似三角形应用举例（教案）
一、教学内容
人教版数学九年级下册27.2.3相似三角形应用举例。本节课主要内容包括：
1.探索并理解相似三角形在现实生活中的应用，如测量物体长度、距离等。
2.学会运用相似三角形的性质解决实际问题，包括直角三角形、等腰三角形以及一般三角形的相似问题。
九年级数学下册第二十七章相似27.2相似三角形3相似三角形应用举例作业课件新版新人教版
6．(2020·上海)《九章算术》中记载了一种测量井深的方法．如图所示， 在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C， 视线DC与井口的直径AB交于点E，如果测得AB＝1.6米，BD＝1米，BE＝ 0.2米，那么井深AC为_________7米．
7．周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时， 他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸 边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延 长线上选择点D，竖起标杆DE，使得点E与点C，A共线． 已知：CB⊥AD，ED⊥AD，测得BC＝1 m，DE＝1.5 m，BD＝8.5 m．测 量示意图如图所示．请根据相关测量信息，求河宽AB的长度．
解：设 BN 的长为 x 米，则 BM＝x＋1.1＋2.8－1.5＝(x＋2.4)米．由题 意，得∠CND＝∠ANB，∠CDN＝∠ABN＝90°，∴△CND∽△ANB， ∴CADB ＝DBNN .同理，△EMF∽△AMB，∴AEFB ＝BFMM .∵EF＝CD， ∴DBNN ＝BFMM ，即1x.1 ＝x＋1.52.4 .解得 x＝6.6，∵CADB ＝DBNN ，∴A1.B6
解：∵BC⊥AD，DE⊥AD，∴BC∥DE，∴△ABC∽△ADE，∴BDCE ＝AADB ，∴11.5 ＝ABA＋B8.5 ，解得 AB＝17 m.经检验，AB＝17 是 分式方程的解．答：河宽 AB 的长度为 17 m．
8．如图，某同学用自制的直角三角形纸板DEF测量树的高度AB，他 调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直 线上．已知纸板的两条直角边DE＝40 cm，EF＝20 cm，测得边DF离 地面的高度AC＝1.5 m，CD＝8 m，则树高AB是( D ) A．4米 B．4.5米 C．5米 D．5.5米
人教版初中数学相似三角形应用举例优质课件下载
•
4.做好这类题首先要让学生对所给材 料有准 确的把 握，然 后充分 调动已 有的知 识和经 验再迁 移到文 段中来 。开放 性试题 ，虽然 没有规 定唯一 的答案 ，可以 各抒已 见，但 在答题 时要就 材料内 容来回 答问题 。
•
5.木质材料由纵向纤维构成，只在纵 向上具 备强度 和韧性 ，横向 容易折 断。榫 卯通过 变换其 受力方 式，使 受力点 作用于 纵向， 避弱就 强。
四、课堂练习：
1、如图，为估算学校的旗杆的高度，身高 1.6 米的张良同学沿着
旗杆在地面上的影子 AB 由点 A 向点 B 走去，当他走到点 C 处时，
她的影子的顶端正好与旗杆的影子的顶端重合，此时测得 AC＝2 m，
C BC＝8 m，则旗杆的高度是( )
A.6.4 m B．7 m
C．8 m
D．9 m
•
8.正是在大米的哺育下，中国南方地 区出现 了加速 度的文 明发展 轨迹。 河姆渡 文化之 后，杭 嘉湖地 区兴盛 起来的 良渚文 化，在 东亚大 陆率先 迈上了 文明社 会的台 阶，成 熟发达 的稻作 农业是 其依赖 的社会 经济基 础。
•
9.考查对文章内容信息的筛选有效信 息的能 力。这 类试题 ，首先 要明确 信息筛 选的方 向，即 挑选的 范围和 标准， 其次要 对原文 语句进 行加工 ，用凝 练的语 言来作 答。
•
2.该类题目考察学生对文本的理解， 在一定 程度上 是在考 察学生 对这类 题型答 题思路 。因此 一定要 将这些 答题技 巧熟记 于心， 才能自 如运用 。
•
3. 结合实际，结合原文，根据知识库 存，发 散思维 ，大胆 想象。 由文章 内容延 伸到现 实生活 ，对现 实生活 中相关 现象进 行解释 。对人 类关注 的环境 问题等 提出解 决的方 法，这 种题考 查的是 学生的 综合能 力，考 查的是 学生对 生活的 关注情 况。
最新人教版九年级数学下册27.2.3：相似三角形的应用举例课件
相交于点C。此时，测得DE 、 BC、BD就可以求两岸间
的大致距离AB了。
A
此时如果测得DE＝120米， BC＝60米，BD＝50米，求
两岸间的大致距离AB． B
请同学们自已解答
并进行交流
D
C
E
例4:为了估算河的宽度,我们可以在河对岸 选定一个目标点P,在近岸取点Q和S,使点P、 Q、S共线且直线PS与河垂直，接着在过点 S且与PS垂直的直线a上选择适当的点T,确 定PT与过点Q且垂直PS的直线b的交点R.如 果测得QS=45m,ST=90m,QR=60m, 求河的宽度PQ.
分别根据上述两种不同方 A
法求出树高（精确到0.1M）
C
请你自己写出求解过程，
并与同伴探讨，还有其
B
他测量树高的方法吗？
D
E
5.小华为了测量所住楼房的高度，他请来 同学帮忙，测量了同一时刻他自己的影长 和楼房的影长分别是0.5米和15米．已知小 华的身高为1.6米，那么他所住楼房的高度 为 米．
6.如图，一条河的两岸有一段是平行的，在
A D
B
CE F
7.教学楼旁边有一棵树，数学兴趣小组的同 学们想利用树影测量树高。课外活动时在阳 光下他们测得一根长为1米的竹竿的影长是 0.9米，但当他们马上测量树高时，发现树的 影子不全落在地面上，有一部分影子落在教 学楼的墙壁上。他们测得落在地面的影长2.7 米，落在墙壁上的影长1.2米，请你和他们一 起算一下，树高多少米？
P
Q Rb
a
S
T
P
例题
求河宽?
45m
解：∵∠PQR=∠PST= 90° ∠P=∠P
∴ △PQR ∽△PST
60m QR
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FH 5 12 1.6
解得FH=8.
当他与左边较低的树的距离小 于8m时，就不能看到右边较高 的树的顶端点C。 WXQ
此时如果测得BD＝120米，DC＝60米，EC＝50米，求两 岸间的大致距离AB．
A
BDC EWXQ应用举例2
此时如果测得BD＝120米，DC＝60米，EC＝50 米，求两岸间的大致距离AB．
解： 因为 ∠ADB＝∠EDC，
∠ABC＝∠ECD＝90°，
所以 △ABD∽△ECD，
AB BD 那么 EC DC
A OB
EF
1.数学兴趣小组测校内一棵树高，如图，把镜子 放在离树（AB）8m点E处，然后沿着直线BE后 退到D，这时恰好在镜子里看到树梢顶点A，再 用皮尺量得DE=2m，观察者目高CD=1.6m。树 高多少米？
A C
E D
WXQ
B
应用举例2
如图，为了估算河的宽度，我们可以在河对岸选定一个目 标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后， 再选点E，使EC⊥BC，用视线确定BC和AE的交点D．
埃及著名的考古专家穆罕穆 德决定重新测量胡夫金字塔 的高度.在一个烈日高照的上 午.他和儿子小穆罕穆德来到 了金字塔脚下,他想考一考年 仅15岁的小穆罕穆德.
给你一条2米高的 木杆,一把皮尺. 你能利用所学知 识来测出塔高吗?
2米木杆
皮尺
例1：据史料记载，古希腊数学家、天文学家泰勒斯 曾利用相似三角形的原理，在金字塔影子的顶部立一 根木杆，借助太阳光线构成两个相似三角形，来测量 金字塔的高度。 如图，如果木杆EF长2m，它的影长FD为3 m，测得OA 为201 m，求金字塔的高度BO B E 2m O 201m 3m D
A(F)
B E 2m O 201m 3m D
A(F)
解：太阳光是平行线， 因此∠BAO= ∠EDF
又 ∠AOB= ∠DFE=90° ∴△ABO∽△DEF BO OA = EF FD OA· EF 201×2 BO = = = 134 FD 3
1.小华为了测量所住楼房的高度，他请来同学 帮忙，测量了同一时刻他自己的影长和楼房的 影长分别是0.5米和15米．已知小华的身高为 1.6米，那么他所住楼房的高度为 米．
A
B
D
C
E
WXQ
此时如果测得BD＝45米， DE＝90米，BC＝60米， 求两岸间的大致距离AB．
4、 已知左、右并排的两棵大树的高分别是 AB=8m和CD=12m，两树的根部的距离 BD=5m，一个身高1.6m的人沿着正 对这两棵树的一条水平直路l从左 向右前进，当他与左边较低的树的距离小于多少时， 就不能看到右边较高的树的顶端点C？
27.2.2 相似三角形应用举例
复习回顾 1、判断两三角形相似有哪些方法?
定义，平行法，(SSS)，(SAS)，(AA)，(HL)
2、相似三角形有什么性质？
（1）对应边的比相等，对应角相等 （2）相似三角形的周长比等于相似比 （3）相似三角形的面积比等于相似比的平方 （4）相似三角形的对应边上的高、中线、角 平分线的长度比等于相似比
BD EC 120 50 解得AB 100(米) DC 60 WXQ 答： 两岸间的大致距离为 100米．
一题多解
我们还可以在河对岸选定一目标点A，再在河的一边选 点D和 E，使DE⊥AD，然后，再选点B，作BC∥DE， 与视线EA相交于点C。此时，测得DE , BC, BD, 就可 以求两岸间的大致距离AB了。
设观察者眼晴的位置（视点） 为F，∠CFK和∠AFH分别是 观察点C、A的仰角，区域Ⅰ 和区域Ⅱ都在观察者看不到 的区域（盲区）之内。 WXQ
解：假设观察者从左向右走到点E时，他的眼睛的 位置点F与两棵树的顶端点A、C在一条直线上。 ∵AB⊥L，CD⊥L， ∴AB∥CD，△AFH∽△CFK， FH AH ∴ FK CK 即 FH 8 1 .6 ，
WXQ
图11
3、如图，有一路灯杆AB(底部B不能直接到达)，路 灯杆AB的高度8m，小明得身高为1.6m,小明在距灯 的底部（B处)20m的点F处沿NB方向行走14米到达点 B处,人影的长度变化了多少？
A
C O
E G
B
N
F
一题多解 还可以有其他方法测量吗？
B
E
┐ F △ABO∽△AEF 平面镜 ┐ O = OA AF
WXQ
2.教学楼旁边有一棵树，数学兴趣小组的同学们想利用树 影测量树高。课外活动时在阳光下他们测得一根长为 1米 的竹竿的影长是0.9米，但当他们马上测量树高时，发现 树的影子不全落在地面上，有一部分影子落在教学楼的墙 壁上。他们测得落在地面的影长2.7米，落在墙壁上的影 长1.2米，请你和他们一起算一下，树高多少米？
解得FH=8.
当他与左边较低的树的距离小 于8m时，就不能看到右边较高 的树的顶端点C。 WXQ
此时如果测得BD＝120米，DC＝60米，EC＝50米，求两 岸间的大致距离AB．
A
BDC EWXQ应用举例2
此时如果测得BD＝120米，DC＝60米，EC＝50 米，求两岸间的大致距离AB．
解： 因为 ∠ADB＝∠EDC，
∠ABC＝∠ECD＝90°，
所以 △ABD∽△ECD，
AB BD 那么 EC DC
A OB
EF
1.数学兴趣小组测校内一棵树高，如图，把镜子 放在离树（AB）8m点E处，然后沿着直线BE后 退到D，这时恰好在镜子里看到树梢顶点A，再 用皮尺量得DE=2m，观察者目高CD=1.6m。树 高多少米？
A C
E D
WXQ
B
应用举例2
如图，为了估算河的宽度，我们可以在河对岸选定一个目 标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后， 再选点E，使EC⊥BC，用视线确定BC和AE的交点D．
埃及著名的考古专家穆罕穆 德决定重新测量胡夫金字塔 的高度.在一个烈日高照的上 午.他和儿子小穆罕穆德来到 了金字塔脚下,他想考一考年 仅15岁的小穆罕穆德.
给你一条2米高的 木杆,一把皮尺. 你能利用所学知 识来测出塔高吗?
2米木杆
皮尺
例1：据史料记载，古希腊数学家、天文学家泰勒斯 曾利用相似三角形的原理，在金字塔影子的顶部立一 根木杆，借助太阳光线构成两个相似三角形，来测量 金字塔的高度。 如图，如果木杆EF长2m，它的影长FD为3 m，测得OA 为201 m，求金字塔的高度BO B E 2m O 201m 3m D
A(F)
B E 2m O 201m 3m D
A(F)
解：太阳光是平行线， 因此∠BAO= ∠EDF
又 ∠AOB= ∠DFE=90° ∴△ABO∽△DEF BO OA = EF FD OA· EF 201×2 BO = = = 134 FD 3
1.小华为了测量所住楼房的高度，他请来同学 帮忙，测量了同一时刻他自己的影长和楼房的 影长分别是0.5米和15米．已知小华的身高为 1.6米，那么他所住楼房的高度为 米．
A
B
D
C
E
WXQ
此时如果测得BD＝45米， DE＝90米，BC＝60米， 求两岸间的大致距离AB．
4、 已知左、右并排的两棵大树的高分别是 AB=8m和CD=12m，两树的根部的距离 BD=5m，一个身高1.6m的人沿着正 对这两棵树的一条水平直路l从左 向右前进，当他与左边较低的树的距离小于多少时， 就不能看到右边较高的树的顶端点C？
27.2.2 相似三角形应用举例
复习回顾 1、判断两三角形相似有哪些方法?
定义，平行法，(SSS)，(SAS)，(AA)，(HL)
2、相似三角形有什么性质？
（1）对应边的比相等，对应角相等 （2）相似三角形的周长比等于相似比 （3）相似三角形的面积比等于相似比的平方 （4）相似三角形的对应边上的高、中线、角 平分线的长度比等于相似比
BD EC 120 50 解得AB 100(米) DC 60 WXQ 答： 两岸间的大致距离为 100米．
一题多解
我们还可以在河对岸选定一目标点A，再在河的一边选 点D和 E，使DE⊥AD，然后，再选点B，作BC∥DE， 与视线EA相交于点C。此时，测得DE , BC, BD, 就可 以求两岸间的大致距离AB了。
设观察者眼晴的位置（视点） 为F，∠CFK和∠AFH分别是 观察点C、A的仰角，区域Ⅰ 和区域Ⅱ都在观察者看不到 的区域（盲区）之内。 WXQ
解：假设观察者从左向右走到点E时，他的眼睛的 位置点F与两棵树的顶端点A、C在一条直线上。 ∵AB⊥L，CD⊥L， ∴AB∥CD，△AFH∽△CFK， FH AH ∴ FK CK 即 FH 8 1 .6 ，
WXQ
图11
3、如图，有一路灯杆AB(底部B不能直接到达)，路 灯杆AB的高度8m，小明得身高为1.6m,小明在距灯 的底部（B处)20m的点F处沿NB方向行走14米到达点 B处,人影的长度变化了多少？
A
C O
E G
B
N
F
一题多解 还可以有其他方法测量吗？
B
E
┐ F △ABO∽△AEF 平面镜 ┐ O = OA AF
WXQ
2.教学楼旁边有一棵树，数学兴趣小组的同学们想利用树 影测量树高。课外活动时在阳光下他们测得一根长为 1米 的竹竿的影长是0.9米，但当他们马上测量树高时，发现 树的影子不全落在地面上，有一部分影子落在教学楼的墙 壁上。他们测得落在地面的影长2.7米，落在墙壁上的影 长1.2米，请你和他们一起算一下，树高多少米？