三角形梯形的面积(2)

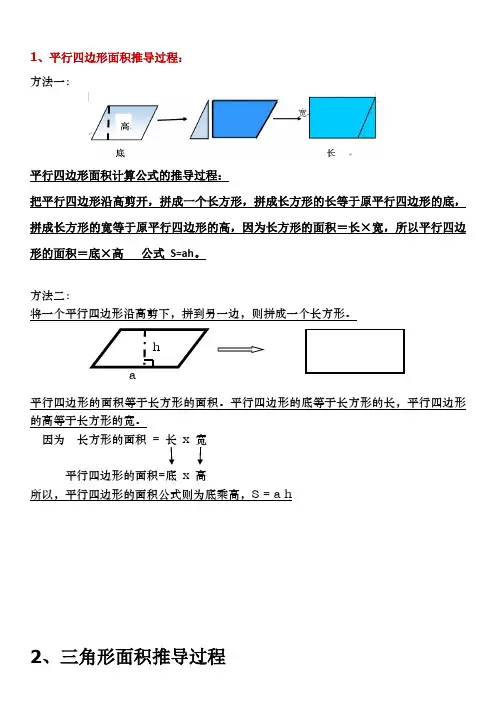
1、平行四边形面积推导过程：
方法一：
平行四边形面积计算公式的推导过程：
把平行四边形沿高剪开，拼成一个长方形，拼成长方形的长等于原平行四边形的底，拼成长方形的宽等于原平行四边形的高，因为长方形的面积＝长×宽，所以平行四边形的面积＝底×高公式S=ah。

方法二：
将一个平行四边形沿高剪下，拼到另一边，则拼成一个长方形。

平行四边形的面积等于长方形的面积。

平行四边形的底等于长方形的长，平行四边形的高等于长方形的宽。

因为长方形的面积= 长х宽
平行四边形的面积=底х高
所以，平行四边形的面积公式则为底乘高，S = a h
2、三角形面积推导过程
两个完全一样的三角形能拼成一个平行四边形，三角形的面积是拼成平行四边形面积
面积÷2=底×高÷2 ，公式S= a×h÷2
3、梯形面积推导过程
两个完全一样的梯形可以拼成一个平行四边形，原梯形的面积是拼成平行四边形面积的一半，拼成平行四边形的底是原梯形的上底与下底的和，拼成平行四边形的高是原梯形的高，所以梯形的面积=（上底+下底）×高÷2 公式S=(a+b)×h÷2；。

三角形和四边形的面积求法三角形和四边形是常见的几何形状，在数学和几何学中经常会涉及到它们的面积计算。

本文将分别介绍三角形和四边形的面积求法，并给出详细的计算方法。

一、三角形的面积求法：三角形是由三条边连接而成的平面图形，根据三角形的特点，我们可以通过不同的方式计算三角形的面积。

1.通过底和高计算：当我们已知三角形的底和高时，可以利用以下公式计算三角形的面积：面积=底×高÷ 22.通过两边和夹角计算：当我们已知两条边和它们之间的夹角时，可以利用以下公式计算三角形的面积：面积= 1/2 ×边1 ×边2 × sin(夹角)3.通过三边长度计算：当我们已知三条边的长度时，可以利用以下公式计算三角形的面积：面积= √[p × (p -边1) × (p -边2) × (p -边3)]其中，p = (边1 +边2 +边3) ÷ 2二、四边形的面积求法：四边形是由四条边连接而成的平面图形，不同的四边形有不同的面积计算方法。

下面将介绍几种常见四边形的面积求法。

1.长方形的面积求法：长方形由长和宽组成，可以利用以下公式计算长方形的面积：面积=长×宽2.正方形的面积求法：正方形的四边长度相等，可以利用以下公式计算正方形的面积：面积=边长×边长或面积=边长的平方3.平行四边形的面积求法：平行四边形的面积可以通过底和高计算，可以利用以下公式计算平行四边形的面积：面积=底×高4.梯形的面积求法：梯形由上底、下底和高组成，可以利用以下公式计算梯形的面积：面积= (上底+下底) ×高÷ 2通过以上公式和方法，我们可以在不同情况下准确地计算三角形和四边形的面积。

当然，在实际应用中，也可以根据需要灵活运用其他数学原理和几何定理来求解面积问题。

需要注意的是，在进行面积计算时，应该确保所使用的单位是一致的，例如，如果底的单位是米，那么高的单位也应该是米，面积的单位就是平方米。

1、已知右图的上底是20厘米，下底是34厘米，其中阴影部分的面积是340平方厘米。

这个梯形的面积是多少？2、已知下图梯形的面积是252平方米，空白部分为平行四边形,求阴影部分的面积。

（单位：米）3、在一个底为6分米，高为15分米的直角三角形右侧对接上一个梯形（阴影部分）拼成了一个平行四边形，求这个梯形的面积。

4、一块直角梯形的地，它的下底是40米，如果上底增加38米，这块地就变成了正方形，原来梯形的面积是多少？5、如下图，一个平行四边形被分成甲、乙两部分，甲的面积比乙大32平方米，甲的上底是多少米？2、有一个梯形，如果它的上底增加2米，下底和高都不变，它的面积就增加4．8平方米；如果下底和上底都不变，高增加2米，它的面积就增加8．5平方米。

求原来梯形的面积。

7、一个长方形纸折成如下梯形的形状，AE=AD，AB边长10厘米，求梯形ABCD的面积。

8、一块三角形地的底是24米，高15米。

这块地的面积是多少平方米？9、一块平行四边形的麦地，底是230米，高是80米，每平方米收小麦5千克。

这块地共收小麦多少千克?一、填空20301.利用割补法，可以把一个平行四边形转化成一个（），它的面积与平行四边形的面积（），它的（）与平行四边形的底相等，它的（）与平行四边形的高相等。

因为它的面积等于（），所以平行四边形边的面积等于（）。

2．平行四边形的面积公式用字母表示可以写作（），也可以写作（）。

还可以写作（）。

；三角形的面积的计算公式用字母表示是（）。

3. 平行四边形的底是2分米5厘米，高是底的1.2倍，它的面积是（）平方厘米。

4.一个三角形的底是4分米，高是30厘米，面积是（）平方分米。

5.一个三角形的高是7分米，底是8分米，和它等底等高的平行四边形的面积是（）平方分米。

6.一个三角形的面积是4.8平方米，与它等底等高的平行四边形的面积是（）7．一个平行四边形的面积是280平方厘米，与它的等底等高的三角形的面积是（）平方厘米。

三角形：面积=底×高÷2 ——【底=面积×2÷高；高=面积×2字母公式： S=ah÷2 h=2S÷a a=2S÷h梯形：面积=（上底+下底）×高÷字母公式： S=（a+b）h÷2 a=2S÷h-b b=2S÷h-a a+b=2S÷h h=2S÷（a+b）三角形面积公式推导：旋转两个完全一样的三角形可以拼成一个平行四边形，长方形的长相当于平行四边形的底；平行四边形的底相当于三角形的底；长方形的宽相当于平行四边形的高；平行四边形的高相当于三角形的高；长方形的面积等于平行四边形的面积，平行四边形的面积等于三角形面积的2倍，因为长方形面积=长×宽，所以平行四边形面积=底×高。

因为平行四边形面积=底×高，所以三角形面积=底×高÷2两个完全一样的梯形可以拼成一个平行四边形，知道就行。

平行四边形的底相当于梯形的上下底之和；平行四边形的高相当于梯形的高；平行四边形面积等于梯形面积的2倍，因为平行四边形面积=底×高，所以梯形面积=(上底+下底)×高÷2等底等高的平行四边形面积相等；等底等高的三角形面积相等；等底等高的平行四边形面积是三角形面积的2倍。

例1.三角形的面积公式用字母表示为（ ）。

一个三角形底长9cm ，高是6cm ，它的面积是（ ）。

一个平行四边形的面积是2.4平方米，和它等底等高的三角形的面积是（ ）平方米。

一个直角三角形的两条直角边分别是5厘米和8厘米，这个三角形的面积是（ ）平方厘米。

变式：1.两个完全相同的直角三角形一定能拼成一个长方形。

（ ）2.两个面积相等的三角形，它们的底和高一定相等。

（ ）3.三角形的面积等于平行四边形面积的一半。

（ ）4.等底等高的三角形的面积相等。

《三角形和梯形的面积》教学设计长兴县煤山镇中心小学王园飞教学内容人教版《义务教育教科书·数学》五年级上册第六单元多边形的面积“三角形和梯形的面积”及相关练习。

课例说明《三角形和梯形的面积》是人教版五年级上册第五单元的知识，本课内容是对三角形和梯形的面积的整合，引导学生把三角形和梯形转化成已学过的图形来推导面积计算公式，然后利用面积计算公式解决生活中的应用问题。

教学中提供给学生几种不同形状的三角形和梯形去探究，目的是让学生经历从特殊到一般的归纳过程。

有了操作和讨论作铺垫，公式的推导也就水到渠成了，所以，让他们自己推公式。

在“操作、观察、分析、讨论、概括、归纳”这一系列的数学活动中，学生亲历了一个知识再创造的过程，体验到成功的喜悦。

教学目标1.使学生在理解的基础上探索并掌握三角形和梯形的面积计算公式的推导过程,能利用公式求三角形和梯形的面积。

2.掌握转化的思想和方法,进一步明白事物之间是相互联系,可以转化的。

教学重点三角形和梯形面积计算公式的推导和利用教学难点运用转化的方法探究三角形和梯形的面积计算公式教学具准备剪刀,一个梯形，方格纸教学过程一、复习欣赏、引入新课。

1.展示生活中的三角形梯形,温故引新师:这就是我们生活中的三角形和梯形。

你能说出它各部分的名称吗?请你边说边用你的小手指一指.你还想知道什么?(出示课件)生:面积2.出示课题师：今天我们继续用转化的方法学习三角形和梯形的面积。

（板书课题：三角形和梯形的面积）师：谁知道三角形或梯形的面积公式？用字母怎么表示？【设计意图】本环就展开想象，在兴趣盎然的状态中打开了思维，培养了学生以发展的眼光看数学，逐步建构自己知识体系的能力,初步感知解决问题的途径和方法.二、提供材料、动手操作、公式推导。

任务一、猜想三角形和梯形面积公式可能的推导过程师：谁愿意猜一猜三角形和梯形面积的计算公式可能是怎样推导出来的？生1：用两个完全一样的三角形拼成平行四边形，用两个完全一样的梯形拼成平行四边形生2：把个梯形分割成两个三角形生3：把一个三角形转化成一个平行四边形来推导，把一个梯形转化成三角形来推导生4: 把一个梯形转化成平行四边形来推导师：同学们对梯形面积的计算公式推导作了大胆的猜想，但光有猜想是不够的，我们还要进行探索研究，通过事实来说明。

广州市博尔雅教育中心五年级数学暑假班第15讲三角形和梯形的面积例1、一块三角形的菜地底边长100厘米，它的高22厘米。

求菜地的面积？例2、已知，如图，三角形ABC 的面积为54cm 2，找出三角形ABC 的底和高，并求出BD的长。

例3、一块近似梯形的挡风玻璃，上底132cm ，下底105cm ，高50cm 。

这块挡风玻璃的面积大约是多少？例4、一个梯形的面积是60平方厘米, 上底与下底的和是20厘米, 求梯形的高。

1.计算下面三角形的面积 （单位cm ）574 3.64.52.78m 3. 你能求下图三角形斜边上的高吗？4.计算下面梯形的面积 （单位cm ）5. 利用一面墙，用篱笆围成一块梯形菜地，已知篱笆全长35米，求菜地的面积是多少平方米？6.一块近似梯形的菜地,上底长32米,下底比上底多16米,高是8米,这块菜地的面积是多少平方米?如果每平方米种菜50棵 ，一共可以种多少棵？、图中有哪两个三角形的面积相等？你能找出几组？35 cm4.8 cm2、一块平行四边形的草地中有一条长8m 、宽1m 的小路，求草地的面积。

3、下图中阴影部分的面积是10平方厘米，三角形ABC4、图中是两个完全相同的直角三角形叠在一起的，求阴影部分的面积。

（单位：分米）一、判断题1.两个面积相等的梯形可以拼成一个平行四边形。

（ ）2.梯形面积是三角形面积的2倍。

（ ）3.一个梯形有无数条高。

（ ）4.如果梯形的面积是12平方厘米,两个完全一样的梯形拼成的平行四边形的面积是6平方厘米。

（ ）5.一个梯形上下底的和是20米，高是8米，这个梯形的面积是80平方米。

（ ）6.一个平行四边形可以分成两个梯形 。

（ ）7.两个三角形可以拼成一个长方形。

（ ）8.三角形的面积是长方形面积的一半。

（ ）9.三角形面积是S ＝ah 。

（ ） 10.有两个形状不同的三角形，它们的底、高都相等，那么它们的面积一定相等。

（ ） 二、填空题。

梯形面积计算方法梯形是一种特殊的四边形，它有两对平行的边，其中一对边较长，另一对边较短。

计算梯形的面积可以使用特定的公式，或者通过将梯形分解为矩形和三角形来计算。

下面将介绍两种常用的梯形面积计算方法。

方法一：使用梯形面积公式梯形的面积可以使用以下公式进行计算：面积 = （上底 + 下底）× 高÷ 2其中，上底和下底分别表示梯形的两条平行边的长度，高表示梯形的高度。

假设有一个梯形，上底长度为a，下底长度为b，高度为h，那么可以使用上述公式计算其面积。

例如，如果上底长度为5cm，下底长度为8cm，高度为4cm，则梯形的面积为：面积 = （5 + 8）× 4 ÷ 2 = 26 平方厘米方法二：分解为矩形和三角形除了使用公式计算梯形的面积外，还可以将梯形分解为矩形和三角形，分别计算它们的面积，然后将结果相加。

将梯形划分为一个矩形和两个三角形。

矩形的长度为梯形的高度，宽度为梯形上底和下底的平均值。

两个三角形的面积可以使用以下公式计算：三角形面积 = 底边长度× 高度÷ 2然后，将矩形和两个三角形的面积相加，即可得到梯形的总面积。

例如，假设有一个梯形，上底长度为6cm，下底长度为10cm，高度为3cm。

首先计算矩形的面积，矩形的长度为3cm，宽度为（6+10）÷ 2 = 8cm。

因此，矩形的面积为3cm × 8cm = 24平方厘米。

接下来，计算两个三角形的面积。

第一个三角形的底边长度为6cm，高度为3cm，面积为6cm × 3cm ÷ 2 = 9平方厘米。

第二个三角形的底边长度为10cm，高度为3cm，面积为10cm × 3cm ÷ 2 = 15平方厘米。

将矩形和两个三角形的面积相加，即可得到梯形的总面积：总面积 = 矩形面积 + 两个三角形面积 = 24 平方厘米 + 9 平方厘米 + 15 平方厘米 = 48 平方厘米梯形的面积计算方法主要有两种：使用梯形面积公式和分解为矩形和三角形。

梯形的面积知识点梯形是初中数学中常见的一个几何形状，计算梯形的面积是考察学生几何计算能力的重要内容。

本文将介绍梯形的定义、性质以及计算梯形面积的方法。

一、梯形的定义和性质梯形是一个四边形，其中两条边是平行的，这两条平行边称为梯形的上底和下底，两边不平行的边称为梯形的斜边，梯形的高是从上底垂直地落到下底的一条垂线段。

梯形的性质如下：1. 梯形的对角线长度相等。

梯形的对角线是从一个非平行边的一个顶点连接到另一条非平行边的对角线，对角线的长度相等。

2. 梯形的相邻内角互补。

梯形的相邻内角是指具有一个公共顶点且内部没有其他角的连续两个角，这两个角的和是180度。

3. 梯形的底角和顶角互补。

梯形的底角是指与梯形的下底相对的两个内角，底角的和与顶角的和是180度。

二、计算梯形面积的方法计算梯形的面积可以使用以下两种方法：一种是使用梯形的面积公式，另一种是将梯形拆分成两个三角形进行计算。

1. 面积公式：梯形的面积公式为：面积 = （上底 + 下底）×高 ÷ 2其中，上底和下底分别表示梯形的两个平行边的长度，高表示从上底垂直落到下底的垂直距离。

例如，给定梯形的上底为6cm，下底为10cm，高为4cm，可以使用面积公式计算：面积 = （6 + 10）× 4 ÷ 2 = 16 cm²2. 拆分成两个三角形计算：将梯形分成两个三角形，然后计算两个三角形的面积，最后将两个三角形的面积相加即可得到梯形的面积。

例如，给定梯形的上底为6cm，下底为10cm，高为4cm，先计算两个三角形的面积：第一个三角形的面积 = 底 ×高 ÷ 2 = 6 × 4 ÷ 2 = 12 cm²第二个三角形的面积 = 底 ×高 ÷ 2 = 10 × 4 ÷ 2 = 20 cm²最后，将两个三角形的面积相加：12 cm² + 20 cm² = 32 cm²三、应用梯形面积的例题例题1：求梯形ABCD的面积，已知上底AB=8cm，下底CD=12cm，高EF=6cm。