常用逻辑用语复习小结(精华)

常用逻辑用语知识点总结命题：1、定义：我们把用语言、符号或式子表达的，可以判断真假的陈述句叫做命题。

其中判断为真的语句叫做真命题，判断为假的语句叫做假命题．注：1、疑问句、祈使句、感叹句都不是命题．2、还有一种语句，如“5x >”、“210x -=”等，语句中含有变量x 或y ，在没有给定这些变量的值之前，是无法确定语句的真假的，这种含有变量的语句叫做开语句（条件命题）．开语句不是命题．含有全称量词的命题，叫做全称命题．含有存在量词的命题，叫做存在性命题全称命题q: ()x q A ,x ∈∀的否定： 存在性命题p: ()x p A ,x ∈∃的否定：基本逻辑联结词“且”“或”“非”用联结词“且”把命题p 和q 联结起来，得到一个新命题，记作p q ∧，读作：“p 且q ” 命题p q ∧真假判断规律：用联结词“或”把命题p 和q 联结起来，得到一个新命题，记作p q ∨，读作：“p 或q ” 命题p q ∨真假判断规律：对命题p 加以否定，得到一个新命题，记作p ⌝，读作“非p ”或“p 的否定” 命题p ⌝真假判断规律：充分条件与必要条件如果p ，则q ，记作p q ⇒，则称p 是q 的 条件；q 是p 的 条件。

如果p q ⇒，且q p ⇒，简称p 是q 的充要条件。

记作p q ⇔设满足条件p 的集合为数集A ，满足条件q 的集合为数集B,若A 是B 的子集，则p 是q 的 条件若A 是B 的真子集，则p 是q 的 条件若A=B ，则p 是q 的 条件若B 是A 的子集，则p 是q 的 条件若B 是A 的真子集，则p 是q 的 条件规律总结： 。

命题的四种形式• 原命题：如果p ，则q ； • 逆命题：如果q ，则p ；• 否命题：如果非p ，则非q ； • 逆否命题：如果非q ，则非p ．原命题与逆命题，否命题与逆否命题是 的命题；原命题与否命题，逆命题与逆否命题是 的命题；原命题与逆否命题，逆命题与否命题是 的命题。

常用逻辑用语知识点总结在数学和日常的逻辑思考中，常用逻辑用语是非常重要的工具，它们帮助我们清晰准确地表达思想、进行推理和判断。

下面就让我们来一起总结一下常用逻辑用语的相关知识点。

一、命题命题是能够判断真假的陈述句。

比如“今天是晴天”，如果今天确实是晴天，那么这个命题就是真的；如果今天不是晴天，那么这个命题就是假的。

需要注意的是，疑问句、祈使句和感叹句都不是命题。

命题又分为真命题和假命题。

真命题就是判断为真的命题，假命题则是判断为假的命题。

二、四种命题及其关系1、原命题：若 p，则 q。

2、逆命题：若 q，则 p。

3、否命题：若¬p，则¬q。

4、逆否命题：若¬q，则¬p。

其中，原命题和逆否命题同真同假，逆命题和否命题同真同假。

这两对关系在推理和证明中经常被用到。

三、充分条件与必要条件如果有“若 p，则q”为真命题，那么 p 是 q 的充分条件，q 是 p 的必要条件。

例如，“如果一个数是偶数，那么这个数能被 2 整除”，“一个数是偶数”就是“这个数能被 2 整除”的充分条件，“这个数能被 2 整除”就是“一个数是偶数”的必要条件。

充分不必要条件：p 能推出 q，但 q 不能推出 p。

必要不充分条件：q 能推出 p，但 p 不能推出 q。

充要条件：p 能推出 q，q 也能推出 p。

四、逻辑联结词1、“且”（∧）：表示两个命题同时成立。

例如，命题 p：今天是星期一；命题 q：今天是晴天。

那么“今天是星期一且今天是晴天”就是用“且”联结的复合命题。

只有当 p 和 q 都为真时，“p 且q”为真。

2、“或”（∨）：表示两个命题至少有一个成立。

例如，“今天是星期一或今天是晴天”，只要 p 和 q 中有一个为真，“p 或q”就为真。

3、“非”（¬）：表示对一个命题的否定。

例如，命题 p：今天是星期一，那么“非p”就是“今天不是星期一”。

当 p 为真时，“非p”为假；当 p 为假时，“非p”为真。

常用逻辑用语—、命题1、命题的概念在数学中用语言、符号或式子表达的，可以判断真假的陈述句叫做命题•其中判断为真的语句叫做真命题，判断为假的语句叫做假命题.2、四种命题及其关系(1) 、四种命题(2) 、四种命题间的逆否关系(3) 、四种命题的真假关系**两个命题互为逆否命题，它们有相同的真假性；*两个命题为互逆命题或互否命题，它们的真假性没有关系.、充分条件与必要条件1、定义1 .如果p? q,则p是q的充分条件，q是p的必要条件.2•如果p? q, q? p，则p是q的充要条件.2、四种条件的判断1.如果若p则q ”为真，记为p q，如果若p则q ”为假，记为p q .2.若p q，则p是q的充分条件，q是p的必要条件3.判断充要条件方法:p q p q(1 )定义法：①p是q的充分不必要条件p q ②p是q的必要不充分条件p qp q p q③p是q的充要条件q p ④p是q的既不充分也不必要条件p q(2)集合法：设P={p}, Q={q},①若P Q,则p是q的充分不必要条件，q是p的必要不充分条件②若P=Q，则p是q的充要条件(q也是p的充要条件).③若P g.Q且Q ^ P，则p是q的既不充分也不必要条件.(3)逆否命题法：①q是p的充分不必要条件p是q的充分不必要条件②q是p的必要不充分条件p是q的充分不必要条件③q是p的充分要条件p是q的充要条件④q是p的既不充分又不必要条件p是q的既不充分又不必要条件三、简单的逻辑联结词⑴命题中的且”或”非”叫做逻辑联结词.①用联结词且”联结命题p和命题q,记作p A q,读作p且q”.②用联结词或”联结命题p和命题q,记作p V q,读作p或q”.③对一个命题p全盘否定，就得到一个新命题，记作？p，读作非p”或p的否定(2)简单复合命题的真值表:*p A q：p、q有一假为假, *p V q：一真为真, .四、量词1、全称量词与存在量词(1)常见的全称量词有：任意一个” 一切”每一个”任给”所有的”等.(2)常见的存在量词有：存在一个”至少有一个”有些”有一个”某个”有的”等.(3)全称量词用符号?”表示；存在量词用符号? ”表示.2全称命题与特称命题(1) 含有全称量词的命题叫全称命题：对M中任意一个x,有p(x)成立”可用符号简记为？x€ M, p(x),读作对任意x属于M，有p(x)成立”.(2) 含有存在量词的命题叫特称命题:存在M中的一个x o,使p(x o)成立"可用符号简记为？x o€ M , P(x o),读作存在M中的兀素x o，使p(x o)成立”3 命题的否定(1) 含有量词命题的否定全称命题p：x M , p(x) 的否定p：x M, p x ；全称命题的否定为存在命题存在命题p：x M, p x 的否定p：x M , p x ；存在命题的否定为全称命题其中p x p (x)是一个关于x的命题.(2) 含有逻辑连接词命题的否定“p 或q ”的否定：“ p 且q” ；p且q ”的否定：“ p或q”(3) “若p则q “命题的否定：只否定结论特别提醒：命题的“否定”与“否命题”是不同的概念，命题的否定：只否定结论；否命题：全否对命题p的否定(即非p)是否定命题p所作的判断，而否命题”是若p则q ”。

常用逻辑用语知识点总结嘿，同学们！咱们今天来好好聊聊常用逻辑用语这个有点神秘但其实挺有趣的知识板块。

先来说说“命题”。

啥是命题呢？简单说，就是能判断真假的陈述句。

比如说，“今天天气真好”，这就不是命题，因为天气好不好得看具体情况，没法直接判断真假。

但“三角形内角和是 180 度”，这就是个命题，因为它肯定是真的嘛！再讲讲“充分条件”和“必要条件”。

这俩家伙就像是一对好兄弟，总是让人有点分不清。

咱来举个例子，比如说你要参加一个比赛，“你努力训练”是“你取得好成绩”的什么条件呢？如果你努力训练了，可能会取得好成绩，但不是一定能取得好成绩，所以“你努力训练”是“你取得好成绩”的必要条件，但不是充分条件。

还有“全称量词与存在量词”。

比如说“所有的同学都很努力”，这里的“所有”就是全称量词；“有些同学喜欢数学”，这里的“有些”就是存在量词。

我记得有一次给学生们讲这些知识的时候，有个同学一脸迷茫地问我：“老师，这些东西学了有啥用啊？”我当时就笑了，跟他说：“你想想啊，假如你长大了去买东西，商家说‘我们所有的商品都质量上乘’，这时候你就得用咱们学的知识判断一下这是不是真的，别被忽悠了呀！”同学们听了都哈哈大笑，但是也明白了这些知识在生活中的用处。

再说说“逻辑联结词”，“且”“或”“非”。

“且”就像是两个人手拉手，必须都满足条件才行；“或”呢，就像是两条路，走其中一条就行；“非”就是反过来，否定原来的说法。

比如说，“今天是晴天且我心情好”，那必须今天真是晴天，而且我心情也确实好，这个命题才成立。

关于常用逻辑用语的题型，那也是五花八门。

有判断命题真假的，有让你找出充分必要条件的，还有让你用逻辑用语表述一些情况的。

这就需要咱们把知识点掌握得牢牢的，做题的时候认真分析。

学习常用逻辑用语就像是在搭建一座思维的大厦，每一块砖都很重要。

只有把基础打扎实了，才能在解题的时候游刃有余。

希望同学们都能在这个知识海洋里畅游，找到属于自己的宝藏！好啦，今天关于常用逻辑用语的知识点就总结到这里，同学们加油哦！。

常用逻辑用语小结课标要求1．命题及其关系① 了解命题及其逆命题、否命题与逆否命题.② 理解必要条件、充分条件与充要条件的意义，会分析四种命题的相互关系.2．简单的逻辑联结词了解逻辑联结词“或”、“且”、“非”的含义.3．全称量词与存在量词① 理解全称量词与存在量词的意义.② 能正确地对含有一个量词的命题进行否定.知识结构知识盘点一．命题1．命题的定义：我们把用语言、符号或式子表达的，可以判断真假的 叫做命题。

其中判断为真的语句叫做 ，判断为假的语句叫做 。

2．命题的结构：在数学中，具有“若p 则q ”这种形式的命题是较为常见的，我们把这种形式的的命题中的p 叫做 ，q 叫做 。

二．四种命题及其相互关系3．四种命题的概念：一般地，用p 和q 分别表示原命题的条件和结论，用p ⌝和q ⌝分别表示p 和q 的否定，于是四种命题的形式就是：原命题：若p 则q ；逆命题： ；否命题： ；逆否命题： 。

关于逆命题、否命题与逆否命题，也可以如下表述：（1）交换原命题的条件和结论，所得的命题是原命题的 ；（2）同时否定原命题的条件和结论，所得的命题是原命题的 ；（3）交换原命题的条件和结论，同时进行否定，所得的命题是原命题的 。

4．四种命题之间的关系四种命题之间的相互关系如下图所示：由上图知逆命题与否命题也互为逆否命题，因此这四种命题的真假之间的关系如下：（1）两个命题互为逆否命题，它们具有相同的 ；（2）两个命题为互逆命题或互否命题，它们的真假性 。

5．反证法由于原命题与它的逆否命题具有相同的真假性，所以我们在直接证明某一命题有困难时，可以通过证明 ，来间接地证明原命题为真命题，这种证明的方法，称作是 。

用反证法证明的步骤如下：（1） ，即假设结论的反面成立；（2）从 出发，经过推理论证得出矛盾；（3）由矛盾判定假设不正确， 。

三．充分条件与必要条件6．若q p ⇒，则p 叫做q 的 条件，则q 叫做p 的 条件；若q p ⇔，则p 叫做q 的 条件，简称为 条件.7．如果q p ⇒且p q ⇒，我们称p 为q 的 条件，如果q p ⇒且p q ⇒，则我们称p 为q 的 条件.四．判断充要条件的方法8．命题判断法设“若p 则q ”为原命题，那么：(1)原命题为真，逆命题为假时，则p 是q 的 条件；(2)原命题为假，逆命题为真时p 是q 的 条件；(3)原命题与逆命题都为真时，p 是q 的 条件；(4) 原命题与逆命题都为假时，p 是q 的 条件.9．集合判断法 从集合的观点看，建立命题q p ,相应的集合：)(|{:x p x A p =成立}，)(|{:x q x B q =成立}，那么：(1)若B A ⊆，则p 是q 的 条件，若B A ≠⊂时，则p 是q 的 条件； (2) 若A B ⊆，则p 是q 的 条件，若A B ≠⊂时，则p 是q 的 条件； (3)若B A =，则p 是q 的 条件，若B A ⊆且A B ⊆时，则p 是q 的 条件.五．逻辑联结词10．逻辑联结词：在数学中，有时会使用一些联结词，如 .11．“p 且q ”记作 ；“p 或q ”记作 ；“非p ”记作 .12．命题q p ∧，q p ∨和p ⌝的真假判断（1）当q p ,都是真命题时，q p ∧为 ；q p ∨为 ；p ⌝为 .（2）当q p ,有一个是真命题时，q p ∧为 ；q p ∨为 .(3) 当q p ,都是假命题时，q p ∧为 ；q p ∨为 ；p ⌝为 .上述语句可以描述为：对于q p ∧而言“一假必假”；对于q p ∨而言“一真必真”；对于p ⌝而言“真假相反”。

常用逻辑用语知识点总结逻辑是一种以证明、推理和推断为基础的理性思维方法。

在日常生活和学术研究中, 人们经常会遇到各种逻辑问题, 如何正确运用逻辑用语是非常重要的。

下面将就常用的逻辑用语进行知识点总结。

一、假言命题1. 假言命题是由“如果……，则……”的句子构成的命题。

它表示的是一种条件关系。

2. 假言命题的充分条件和必要条件。

充分条件是指如果A成立，则B必定成立；必要条件是指B成立就必定是A成立。

3. 常用逻辑连接词：如果……，就……；只要……，就……；每当……，就……。

4. 示例：如果下雨，地面就会湿。

这就是一个假言命题，如果下雨是充分条件，地面湿是必要条件。

5. 常见的假言命题推理错误：偷换充分条件与必要条件；否定假设；无中生有。

二、联言命题1. 联言命题是由“而且”、“也”、“而且还”等词连接的两个或多个简单命题构成的命题。

它表示的是多个条件同时成立的关系。

2. 常用逻辑连接词：而且、又、且、还、除此之外还。

3. 示例：他不但聪明，而且还非常勤奋。

这就是一个联言命题，表示他既聪明又勤奋。

4. 常见的联言命题推理错误：谬误的联言；与联言条件无关；由联言推出联言分解。

三、析言命题1. 析言命题是由“但是”、“除了……还有”等词连接的两个或多个简单命题构成的命题。

它表示的是两个条件相互排斥的关系。

2. 常用逻辑连接词：但是、然而、不过、相反、相反地、与……相反。

3. 示例：他很有学识，但是思维缜密不足。

这就是一个析言命题，表示他虽然有学识，但思维缜密不足。

4. 常见的析言命题推理错误：非提出人之谬误；擅自坚持；不正当引用。

四、复言命题1. 复言命题是由多个简单命题以及相应的逻辑连接词构成的复杂命题。

2. 常用逻辑连接词：如果……，就……；且；但是；不是；如果……则……；不是因为……而是因为……。

3. 示例：如果你努力学习，就一定会取得好成绩。

这就是一个复言命题，由假言命题构成。

5. 常见的复言命题推理错误：对联言的否定；混淆假言及联言；推而广之。

高中数学知识点总结：常用逻辑用语
高中学生在学习中或多或少有一些困惑，的编辑为大家总结了高中数学知识点总结：常用逻辑用语，各位考生可以参考。

常用逻辑用语：
1、四种命题：
⑴原命题：若p则q;⑵逆命题：若q则p;⑶否命题：若 p 则q;⑷逆否命题：若 q则 p
注：1、原命题与逆否命题等价;逆命题与否命题等价。

判断命题真假时注意转化。

2、注意命题的否定与否命题的区别：命题否定形式是 ;否命题是 .命题或的否定是且且的否定是或 .
3、逻辑联结词：
⑴且(and) ：命题形式 p q; p q p q p q p
⑵或(or)：命题形式 p q; 真真真真假
⑶非(not)：命题形式 p . 真假假真假
假真假真真
假假假假真
或命题的真假特点是一真即真，要假全假
且命题的真假特点是一假即假，要真全真
非命题的真假特点是一真一假
4、充要条件
由条件可推出结论，条件是结论成立的充分条件;由结论可推出条件，则条件是结论成立的必要条件。

5、全称命题与特称命题：
短语所有在陈述中表示所述事物的全体，逻辑中通常叫做全称量词，并用符号表示。

含有全体量词的命题，叫做全称命题。

短语有一个或有些或至少有一个在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词，并用符号表示，含有存在量词的命题，叫做存在性命题。

全称命题p： ; 全称命题p的否定 p：。

特称命题p： ; 特称命题p的否定 p：
以上就是高中数学知识点总结：常用逻辑用语的全部内容，更多考试资讯请继续关注!。

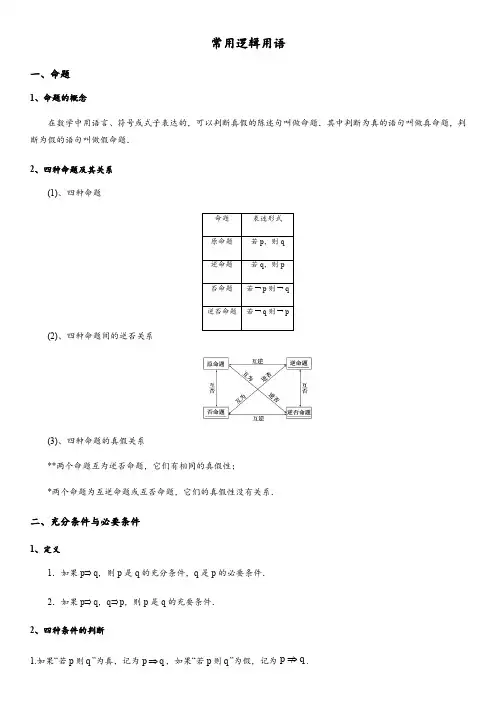
常用逻辑用语一、命题1、命题的概念在数学中用语言、符号或式子表达的，可以判断真假的陈述句叫做命题．其中判断为真的语句叫做真命题，判断为假的语句叫做假命题．2、四种命题及其关系(1)、四种命题(2)、四种命题间的逆否关系(3)、四种命题的真假关系**两个命题互为逆否命题，它们有相同的真假性；*两个命题为互逆命题或互否命题，它们的真假性没有关系．二、充分条件与必要条件1、定义1．如果p⇒q，则p是q的充分条件，q是p的必要条件．2．如果p⇒q，q⇒p，则p是q的充要条件．2、四种条件的判断⇒/.1.如果“若p则q”为真，记为p q⇒，如果“若p则q”为假，记为p q2.若p q⇒，则p是q的充分条件，q是p的必要条件3.判断充要条件方法：（1）定义法：①p是q的充分不必要条件⇔p qp q⇒⎧⎨⇐/⎩②p是q的必要不充分条件⇔p qp q⇒⎧/⎨⇐⎩③p是q的充要条件⇔p qq p⇒⎧⎨⇒⎩④p是q的既不充分也不必要条件⇔p qp q⇒⎧/⎨⇐/⎩（2）集合法：设P={p}，Q={q}，①若P Q，则p是q的充分不必要条件，q是p的必要不充分条件.②若P=Q，则p是q的充要条件（q也是p的充要条件）.③若P Q且Q P，则p是q的既不充分也不必要条件.（3）逆否命题法：①⌝q是⌝p的充分不必要条件⇔p是q的充分不必要条件②⌝q是⌝p的必要不充分条件⇔p是q的充分不必要条件③⌝q是⌝p的充分要条件⇔p是q的充要条件④⌝q是⌝p的既不充分又不必要条件⇔p是q的既不充分又不必要条件三、简单的逻辑联结词(1)命题中的“且”“或”“非”叫做逻辑联结词．①用联结词“且”联结命题p和命题q，记作p∧q，读作“p且q”．②用联结词“或”联结命题p和命题q，记作p∨q，读作“p或q”．③对一个命题p全盘否定，就得到一个新命题，记作¬p，读作“非p”或“p的否定”．(2)简单复合命题的真值表：*p ∧q ： p 、q 有一假为假， *p ∨q ：一真为真， *p 与¬p ：真假相对即一真一假．四、量词1、全称量词与存在量词(1)常见的全称量词有：“任意一个”“一切”“每一个”“任给”“所有的”等．(2)常见的存在量词有：“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等．(3)全称量词用符号“∀”表示；存在量词用符号“∃”表示．2 全称命题与特称命题(1)含有全称量词的命题叫全称命题: “对M 中任意一个x ，有p (x )成立”可用符号简记为∀x ∈M ，p (x )，读作“对任意x 属于M ，有p (x )成立”．(2)含有存在量词的命题叫特称命题: “存在M 中的一个x 0，使p (x 0)成立”可用符号简记为∃x 0∈M ，P (x 0)，读作“存在M 中的元素x 0，使p (x 0)成立”．3命题的否定(1) 含有量词命题的否定全称命题p ：,()x M p x ∀∈的否定⌝p ：(),x M p x ∃∈⌝；全称命题的否定为存在命题存在命题p ：(),x M p x ∃∈的否定⌝p ：(),x M p x ∀∈⌝；存在命题的否定为全称命题其中()p x p （x ）是一个关于x 的命题.(2)含有逻辑连接词命题的否定“p或q”的否定：“⌝p且⌝q”；“p且q”的否定：“⌝p或⌝q”(3)“若p则q“命题的否定：只否定结论特别提醒：命题的“否定”与“否命题”是不同的概念，命题的否定：只否定结论；否命题：全否对命题p的否定（即非p）是否定命题p所作的判断，而“否命题”是“若⌝p则⌝q”。

常用逻辑用语知识点总结在数学的学习中，常用逻辑用语是非常重要的一部分，它能够帮助我们清晰、准确地表达思维和推理过程。

下面就来详细总结一下常用逻辑用语的相关知识点。

一、命题命题是能够判断真假的陈述句。

比如“2 是偶数”，这是一个真命题；“1 ＋ 1 ＝4”，这是一个假命题。

需要注意的是，疑问句、祈使句和感叹句都不是命题。

命题通常用小写字母 p，q，r 等来表示。

根据命题的真假情况，命题可以分为真命题和假命题。

二、四种命题及其关系1、原命题：若 p，则 q。

2、逆命题：若 q，则 p。

3、否命题：若¬p，则¬q。

4、逆否命题：若¬q，则¬p。

原命题和逆否命题、逆命题和否命题互为逆否关系，它们的真假性相同。

例如，原命题“若 a ＞ 0，则 a²＞0”是真命题，那么它的逆否命题“若a² ≤ 0，则a ≤ 0”也是真命题。

三、充分条件与必要条件如果有“若 p，则q”为真命题，那么就说 p 是 q 的充分条件，q 是 p 的必要条件。

比如“若 x ＞ 2，则 x ＞1”，因为 x ＞ 2 能推出 x ＞ 1，所以“x ＞2”是“x ＞1”的充分条件，“x ＞ 1”是“x ＞2”的必要条件。

充分不必要条件：p 能推出 q，但 q 不能推出 p。

必要不充分条件：q 能推出 p，但 p 不能推出 q。

充要条件：p 能推出 q，q 也能推出 p。

四、逻辑联结词1、“且”（∧）：当两个命题 p 和 q 都为真时，p ∧ q 为真；只要有一个为假，p ∧ q 就为假。

例如，命题“2 是偶数且 3 是奇数”是真命题，因为“2 是偶数”和“3是奇数”都是真命题。

2、“或”（∨）：只要两个命题 p 和 q 中有一个为真，p ∨ q 就为真；只有两个都为假时，p ∨ q 才为假。

比如，“2 是奇数或 3 是偶数”是假命题，因为“2 是奇数”和“3 是偶数”都是假命题。

集合与常用逻辑用语知识点总结与归纳本文旨在总结和归纳集合与常用逻辑用语的知识点。

以下是相关概念和要点的简要介绍：集合定义集合是由一组特定元素构成的整体。

常用符号- ∪：表示并集，包括所有在两个或多个集合中的元素。

- ∩：表示交集，包括同时存在于两个或多个集合中的元素。

- ∈：表示元素属于某个集合。

- ∅：表示空集，即不包含任何元素的集合。

常见概念- 子集：如果一个集合的所有元素都属于另一个集合，则前者是后者的子集。

- 真子集：一个集合是另一个集合的真子集，当且仅当它是该集合的子集且不等于该集合本身。

- 并集：两个或多个集合中的所有元素构成的集合。

- 交集：两个或多个集合中共有的元素构成的集合。

逻辑用语常用逻辑符号- ∧：表示逻辑与（and），指两个命题都为真才为真。

- ∨：表示逻辑或（or），指两个命题只要有一个为真就为真。

- ¬：表示逻辑非（not），指对命题的否定。

- ⇒：表示逻辑蕴含（implies），指如果前提为真，则结论也为真。

- ⇔：表示逻辑等价（equivalence），指前提与结论互相为真或互相为假。

常见概念- 命题：陈述性句子，可以判断为真或为假。

- 否定：与命题相反的判断。

- 合取：将多个命题通过逻辑与连接起来的复合命题。

- 析取：将多个命题通过逻辑或连接起来的复合命题。

- 蕴含：由前提推导出结论的关系。

- 等价：前提与结论互相为真或互相为假的关系。

总结本文对集合与常用逻辑用语进行了概念、符号和概念的介绍，希望能够帮助读者更好地理解和应用这些知识点。

深入学习和理解集合和逻辑用语将有助于在不同领域的问题解决和决策过程中的应用。