DH坐标系建立

机械手 D-H 坐标系建立分析孙伏【摘要】D-H method is used widely when analyzing robots and spatial mechanism .However , the fact that there are two joints in middle connecting rod has caused difficulty in understanding and handling in terms of building the linkage ’ coordinate on the previous or rearjoint .On the basis of clarifying the parametric im-plication, the study has tried building and comparing two methods .It shows that the two methods have a-chieved equal results .Through examples , the study analyzes D-H parameter list and kinematical equation with the two methods and comes up with D-H coordination selection method when applying D-H coordinates analy-sis.%在机械手和空间机构分析时，D-H分析法使用广泛。

但是在建立D-H坐标时，中间连杆有两个关节，连杆的坐标是建在前关节还是后关节上，该问题会引起理解和处理的困扰。

在明确了D-H法及其参数含义的基础上，通过两种不同位置D-H坐标的建立和分析对比，说明了两种方法是完全等价的。

通过实例，分析对比了两种方法的D-H参数表和运动学方程，总结出在D-H法分析时D-H坐标选择方法和注意事项。

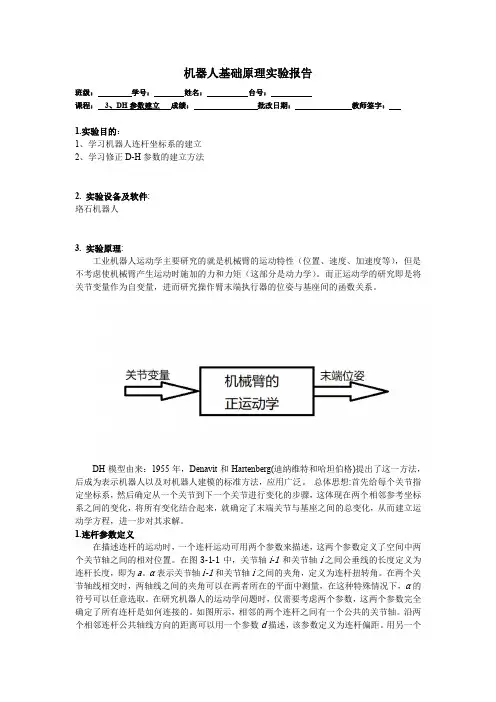
机器人基础原理实验报告班级：学号：姓名：台号：课程：3、DH参数建立成绩：批改日期：教师签字：1.实验目的：1、学习机器人连杆坐标系的建立2、学习修正D-H参数的建立方法2. 实验设备及软件:珞石机器人3. 实验原理:工业机器人运动学主要研究的就是机械臂的运动特性（位置、速度、加速度等），但是不考虑使机械臂产生运动时施加的力和力矩（这部分是动力学）。

而正运动学的研究即是将关节变量作为自变量，进而研究操作臂末端执行器的位姿与基座间的函数关系。

DH模型由来：1955年，Denavit和Hartenberg(迪纳维特和哈坦伯格)提出了这一方法，后成为表示机器人以及对机器人建模的标准方法，应用广泛。

总体思想:首先给每个关节指定坐标系，然后确定从一个关节到下一个关节进行变化的步骤，这体现在两个相邻参考坐标系之间的变化，将所有变化结合起来，就确定了末端关节与基座之间的总变化，从而建立运动学方程，进一步对其求解。

1.连杆参数定义在描述连杆的运动时，一个连杆运动可用两个参数来描述，这两个参数定义了空间中两个关节轴之间的相对位置。

在图3-1-1中，关节轴i-1和关节轴i之间公垂线的长度定义为连杆长度，即为a。

α表示关节轴i-1和关节轴i之间的夹角，定义为连杆扭转角。

在两个关节轴线相交时，两轴线之间的夹角可以在两者所在的平面中测量，在这种特殊情况下，α的符号可以任意选取。

在研究机器人的运动学问题时，仅需要考虑两个参数，这两个参数完全确定了所有连杆是如何连接的。

如图所示，相邻的两个连杆之间有一个公共的关节轴。

沿两个相邻连杆公共轴线方向的距离可以用一个参数d描述，该参数定义为连杆偏距。

用另一个参数描述两相邻连杆绕公共轴线旋转的夹角，该参数称为关节角，记为θ。

图3-1-1 连杆参数的定义(改进DH参数)连杆长度（link length）ai-1：关节轴i-1和关节轴i之间公垂线的长度；连杆扭转角（link twist）αi-1：关节轴i-1和关节轴i投影到垂直于ai-1的平面后构成的角（遵从右手法则，从i-1轴绕ai-1转向i轴）；连杆偏距（link offset）di：沿i轴方向，ai-1和ai的距离，即ai-1与关节轴i的交点到ai与关节轴i的交点的距离；关节角（joint angle）θi：平移ai-1和ai，绕关节轴i旋转成的夹角。

abb机器人的dh参数ABB机器人是世界领先的工业机器人制造商之一，其机器人产品具有高性能、高精度和高可靠性的特点。

为了精确描述ABB机器人的动力学特性，人们常常使用DH参数（Denavit-Hartenberg参数）来建立机器人的运动学模型。

DH参数是用于描述机器人关节之间的几何关系和运动学特性的一种常用方法。

它由四个参数组成：连杆长度、连杆偏移、连杆转角和关节转角。

通过这些参数，可以建立机器人的坐标系，并计算出机器人各个关节之间的转动关系。

我们来看一下ABB机器人的DH参数。

以ABB机器人IRB 120为例，该机器人具有6个自由度，其中第1个关节的DH参数为[a1, α1, d1, θ1]，第2个关节的DH参数为[a2, α2, d2, θ2]，以此类推，直到第6个关节。

这些参数描述了机器人各个关节之间的几何关系和运动学特性。

其中，a表示连杆长度，代表相邻两个关节之间的距离；α表示连杆偏移，代表相邻两个关节之间的旋转轴之间的夹角；d表示连杆转角，代表相邻两个关节之间的位移；θ表示关节转角，代表关节的旋转角度。

通过DH参数，我们可以建立机器人的坐标系，并确定各个关节之间的运动学关系。

例如，对于ABB机器人IRB 120，我们可以通过DH参数计算出机器人末端执行器的位置和姿态。

除了描述机器人的动力学特性，DH参数还可以用于机器人的逆运动学求解。

逆运动学是指根据机器人末端执行器的位置和姿态，求解机器人各个关节的转动角度。

通过DH参数，我们可以建立机器人的正运动学模型，然后利用解析几何和三角学的知识，求解机器人的逆运动学问题。

DH参数在机器人领域中有着广泛的应用。

它不仅可以用于建立机器人的运动学模型和逆运动学模型，还可以用于机器人轨迹规划、动力学分析和控制算法设计等方面。

DH参数是描述机器人动力学特性的重要工具。

通过这些参数，我们可以建立机器人的运动学模型，求解机器人的逆运动学问题，实现机器人的精确控制。

机器人连杆D-H参数及其坐标变换高向东清华大学机械学院在建立坐标变换方程时，把一系列的坐标系建立在连接连杆的关节上，用齐次坐标变换来描述这些坐标之间的相对位置和方向,就可以建立起机器人的运动学方程.现在的问题是如何在每个关节上确定坐标系的方向，以及如何确定相邻两个坐标系之间的相对平移量和旋转量，即需要采用一种合适的方法来描述相邻连杆之间的坐标方向和参数。

常用的是D-H参数法。

D-H参数法Denavit和Hartenberg于1995年提出了一种为关节链中的每一杆件建立坐标系的矩阵方法，即D-H参数法.1.连杆坐标系的建立如图3-15所示，关于建立连杆坐标系的规定如下：（1）z i坐标轴沿i+1关节的轴线方向;（2）x i坐标轴沿z i和z i-1轴的公垂线，且指向背离z i-1轴的方向；（3）y i坐标轴的方向须满足x i轴、z i轴构成x i y i z i右手直角坐标系的条件。

2.连杆参数1）单根连杆参数用两相邻关节轴线间的相对位置关系来描述单根连杆的尺寸，有两个参数。

（1）连杆长度（link length）a i为两关节轴线之间的距离，即z i轴与z i轴的公垂线长度，沿x i轴方向测量.a i总为正值，当两关—1节轴线平行时，a i=l i，l i为连杆的长度；当两关节轴线垂直时，a i=0。

（2）连杆扭角（link twist)αi为两关节轴线之间的夹角，即z i与z i-1轴之间的夹角，绕x i轴从z i—1轴旋转到z i轴，符合右手规则时为正。

当两关节轴线平行时，αi=0;当两关节轴线垂直时，αi=90o.2)相邻连杆之间的参数相邻两连杆之间的参数，用两根公垂线之间的关系来描述.（1）连杆距离（link offset）d i为两根公垂线a i与a i-1之间的距离，即x i轴与x i—1轴之间的距离，在z i—1轴上测量。

对于转动关节,d i为常数；对于移动关节,d i为变量。

（2）连杆转角（joint angle）θi为两根公垂线a i与a i-1之间的夹角，即x i轴与x i-1轴之间的夹角，绕z i—1轴从x i-1轴旋转到x i轴，符合右手规则时为正.对于转动关节，θi为变量；对移动关节，θi为常数。

dh坐标系建立技巧
DH坐标系（Denavit-Hartenberg，简称DH参数法）是一种用于描述机器人连杆结构和关节运动关系的数学方法。

建立DH坐标系时需要遵循一定的原则和技巧：
关节与连杆编号：
1.底座设为Link0，依次对各连杆进行编号。

2.关节i连接的是Link i 和Link i-1。

确定Z轴方向：
1.Z轴通常垂直于关节轴线，并且与关节转动正方向一致，对于旋转
关节，使用右手定则确定其正方向；对于移动关节，则沿直线运动的方向。

确定X轴方向：
1.X轴的选取根据相邻两连杆Z轴之间的相对位置来确定。

1.若Zi与Zi+1不平行也不相交，X轴取作这两轴之间的公垂
线方向，指向Zi+1轴的方向。

2.若Zi与Zi+1平行，可以选择任意一个公垂线作为X轴。

3.若Zi与Zi+1相交，则X轴取为两轴的叉乘方向（右手螺旋
法则）。

确定Y轴方向：
1.Y轴采用右手直角坐标系的规则，通过Zi轴和Xi轴按照右手定则
确定方向。

定义DH参数：
1.DH参数包括四个元素：关节角θ、连杆长度d、关节坐标系原点
相对于前一坐标系的偏移量a以及关节轴线与前一坐标系Z轴的垂直偏移量α。

2.根据上述选定的坐标轴方向，计算每个关节处对应的DH参数。

建立模型矩阵：
1.依据DH参数，可以逐级构建从基坐标系到末端执行器坐标的变换
矩阵，即连杆的模型矩阵A(i)。

在实际应用中，建立DH坐标系是一个反复迭代和调试的过程，确保每一级坐标系正确地反映了机械臂或机器人的连杆和关节特性，以便后续进行正运动学分析和逆运动学求解等任务。

dh坐标系的建立方法## English Answer:### Establishing the DH Coordinate System.The Denavit-Hartenberg (DH) coordinate system is a systematic approach for defining the relative positions and orientations of connected rigid bodies in a robotic or mechanical system. It provides a standardized framework for describing the kinematics and geometry of multi-link assemblies.Steps for Establishing the DH Coordinate System:1. Identify the Base Frame:Determine the fixed reference frame (frame 0) that will serve as the base for the entire system.2. Assign Link Frames:Assign a coordinate frame to each joint or link in the system. These frames will be denoted as {1}, {2}, ..., {n}, where n is the number of links.3. Establish Joint Axes:Define the axis of rotation (z-axis) for each joint. The z-axis should be perpendicular to the plane of motion for revolute joints (Rz) and parallel to the direction of motion for prismatic joints (Tz).4. Determine Common Normals:Identify a vector that is perpendicular to both the z-axis of the current joint and the z-axis of the previous joint. This vector will define the common normal, which is represented as n.5. Assign x-Axes:Assign the x-axis of each link frame to lie in thedirection of the common normal. If there is no common normal, the x-axis can be assigned perpendicular to the z-axis using the right-hand rule.6. Establish y-Axes:Determine the y-axis of each link frame by applying the right-hand rule to the z-axis and x-axis. The y-axis should be perpendicular to both the z-axis and x-axis.7. Define Translation Parameters:Specify the distance along the z-axis between the origins of the adjacent link frames. This parameter is represented as d.8. Define Rotation Parameters:Determine the angle of rotation about the z-axis between the x-axes of adjacent link frames. This parameter is represented as θ.### 中文回答：建立DH坐标系的方法。

dh参数表坐标系的建立DH参数表是用于描述机器人关节之间的几何关系的一种方法。

它是由Denavit-Hartenberg(DH)提出的，用于描述机器人运动学的一种常用方法。

DH参数表的主要作用是将机器人关节之间的几何关系转化为数学表达，从而方便进行运动学分析和控制。

DH参数表一般由四个参数组成，分别是alpha、a、d和theta。

其中，alpha表示相邻两个关节绕z轴旋转的角度，a表示相邻两个关节在x轴上的距离，d表示相邻两个关节在z轴上的距离，theta表示相邻两个关节绕x轴旋转的角度。

通过DH参数表，可以建立起机器人的坐标系。

在建立坐标系时，首先需要确定一个基准坐标系，一般选择机器人的固定坐标系作为基准。

然后，根据DH参数表的定义，逐个关节地建立坐标系。

具体建立坐标系的步骤如下：1.选择一个基准坐标系，一般选择机器人的固定坐标系作为基准。

这个基准坐标系的原点可以选择在机器人的某个关节上，也可以选择在机器人的末端执行器上。

2.逐个关节地建立坐标系。

对于每个关节，根据DH参数表的定义，可以确定该关节的坐标系原点和坐标系的方向。

3.确定坐标系的方向。

根据DH参数表的定义，关节的旋转轴与坐标系的正方向相同，关节的平移轴与坐标系的正方向相反。

4.确定坐标系的原点。

根据DH参数表的定义，关节的旋转轴与坐标系的原点相交，关节的平移轴与坐标系的原点在同一平面上。

5.建立坐标系的坐标轴。

根据坐标系的方向和原点，可以确定坐标系的坐标轴。

通过以上步骤，逐个关节地建立坐标系，就可以得到完整的机器人坐标系。

DH参数表坐标系的建立对于机器人运动学的分析和控制非常重要。

通过建立坐标系，可以方便地描述机器人关节之间的几何关系，从而进行运动学分析和控制。

在实际应用中，DH参数表坐标系的建立也是机器人控制的基础。

DH参数表坐标系的建立是描述机器人关节之间几何关系的一种方法。

通过DH参数表，可以方便地将机器人的关节之间的几何关系转化为数学表达，从而建立起机器人的坐标系。

简述机器人坐标系d-h法的建立方法
DH法（D-H表示Denavit-Hartenberg参数）是机器人学中常用的建立机器人坐标系的方法。

该方法基于以下原则：
1. 坐标系的方向应与机器人的关节轴线一致。

2. 第一个坐标系应与机器人基座相对应。

3. 坐标系的原点应被定义为机器人关节轴线的交点。

4. 坐标系的x轴应指向下一个坐标系原点沿着前一个坐标系z轴方向的投影。

5. y轴应沿着右手法则确定，使得z轴、x轴和y轴构成右手系。

DH法建立机器人坐标系的步骤如下：
1. 确定机器人的关节数和关节类型。

2. 为每个关节定义一个坐标系。

3. 根据关节类型确定每个关节坐标系的变换关系（平移和旋转），并通过设定DH参数进行表述。

4. 将变换矩阵相乘得到机器人所有坐标系之间的变换矩阵，从而得到机器人坐标系（通常选择机器人末端执行器坐标系为目标坐标系）。

DH法能够简便而准确地描述机器人的运动学，是目前机器人学中最常用的方法之一。

大地坐标系建立方法大地坐标系可是个很有趣又很重要的东西呢。

那大地坐标系建立呀，得先确定一个基准面。

这个基准面就像是大地的一个基础舞台。

一般呢，我们会选择参考椭球面作为这个基准面哦。

这个椭球面可不是随便定的，它要尽可能地接近地球的实际形状呢。

想象一下，地球有点像个不太规则的大圆球，这个椭球面就是一个能比较好地贴合它的形状啦。

然后呢，得确定原点的位置。

这个原点就像是坐标系的心脏。

在建立大地坐标系的时候，要精心挑选一个合适的点作为原点。

这个点的选取要考虑到很多因素，比如说在某个国家或者地区的中心位置附近呀，或者是在测量起来比较方便的地方。

接下来就是坐标轴啦。

大地坐标系有坐标轴就像一个大框架的横竖支撑。

通常有X轴、Y轴和Z轴呢。

X轴和Y轴一般是在参考椭球面上确定的方向，Z轴呢就垂直于这个椭球面向外啦。

这些轴的方向和定义都有严格的规定哦，就像大家都要遵守的游戏规则一样。

在建立的过程中呀，还得依靠大量的测量数据。

测量员们就像一群勤劳的小蜜蜂，到处去测量地球上各个点的位置信息。

这些数据就像是拼图的小碎片，把它们都收集起来，经过复杂的计算和调整，才能让这个大地坐标系更加准确。

而且呀，不同的国家和地区可能会根据自己的需求建立自己的大地坐标系。

这就像是每个地方都有自己独特的小天地一样。

不过呢，这些坐标系之间也可以通过一定的转换关系来相互联系，这样在全球范围内大家就都能互相交流位置信息啦。

大地坐标系的建立可不容易呢，它就像是为地球量身打造的一套精确的坐标系统衣服，让我们能够准确地找到地球上的任何一个地方，是不是超级酷呀？。

标准d-h参数法建立六关节臂型机器人的连杆坐标系
标准D-H参数法是一种常用的方法，用于建立机器人的运动
学模型。

在六关节臂型机器人中，每个关节都有一个连杆坐标系。

以下是使用标准D-H参数法建立六关节臂型机器人连杆坐标
系的步骤：
1. 给每个关节定义一个坐标系，通常选择右手坐标系规定方向。

其中，基座（base）使用基座坐标系（坐标系0），末端执行
器（end effector）使用末端坐标系（坐标系N）。

2. 选择一个参考位置，并为每个关节选择一个坐标系原点，通常选取连接轴线的交点作为原点。

3. 根据机器人的结构和运动特点，确定关节坐标系的方向，规定z轴为关节轴线的方向，x轴为连接前一关节与当前关节的
交线的方向。

4. 使用三个转换矩阵描述每个关节的位姿变换，即由前一个关节坐标系到当前关节坐标系的变换关系。

5. 使用DH参数（a, alpha, d, theta）描述每个关节坐标系之间
的相对位移，其中a和alpha表示连接前一关节与当前关节坐
标系原点的距离和连接线与x轴之间的夹角；d表示连接前一
关节与当前关节坐标系原点在z轴方向上的位移；theta表示
连接前一关节与当前关节坐标系原点在z轴方向上的旋转角度。

6. 根据DH参数，建立每两个关节坐标系之间的变换矩阵，乘积即为整个机器人的运动学变换矩阵。

值得注意的是，标准D-H参数法只能用于建立运动学模型，
不考虑机器人的物理约束和动力学特性。

如果需要进行动力学分析和控制，还需要考虑惯性、摩擦等因素，使用更为复杂的方法。

dh法建立机器人运动学方程
DH法（Denavit-Hartenberg法）是一种用于建立机器人运动学方程的方法。

它是由Jacques Denavit和Richard Hartenberg在1955年提出的，用于描述机器人的运动学关系。

DH法将机器人的每个关节作为旋转或平移运动来描述，然后使用一个坐标系来描述每个关节之间的相对位置和方向。

这些坐标系被称为DH 坐标系，它们是固定在机器人上的。

DH法建立机器人运动学方程的步骤如下：
1. 定义坐标系
首先，需要定义一个基准坐标系（通常是世界坐标系），然后为每个关节定义一个本地坐标系。

这些本地坐标系与基准坐标系有一定的相对位置和方向。

2. 建立DH参数表
然后，需要建立一个DH参数表，其中包含每个关节之间的距离、角度和长度等参数。

这些参数将用于计算机器人的运动学方程。

3. 计算转换矩阵
接下来，需要计算从一个本地坐标系到另一个本地坐标系的转换矩阵。

这个转换矩阵可以通过使用DH参数表中定义的参数来计算得出。

4. 建立变换矩阵
然后，需要将每个关节之间的转换矩阵相乘，以建立一个总的变换矩阵。

这个变换矩阵描述了机器人末端执行器相对于基准坐标系的位置
和方向。

5. 建立运动学方程
最后，使用总的变换矩阵来建立机器人的运动学方程。

这个方程可以
用来计算机器人末端执行器在三维空间中的位置和方向。

总之，DH法是一种非常有用的方法，可以用于建立机器人的运动学方程。

它提供了一种简单而有效的方式来描述机器人关节之间的相对位
置和方向，并计算出机器人末端执行器在三维空间中的位置和方向。

标准dh的x轴方向
标准DH（Denavit-Hartenberg）方法是一种用于描述机器人的运动学模型的方法。

在标准DH方法中，x轴方向定义为从前一关节到当前关节的方向。

具体而言，对于每个关节，我们可以定义一个坐标系来描述其位置和方向：
- x轴：与链条的方向一致，从前一关节指向当前关节
- y轴：垂直于链条的方向，向上
- z轴：垂直于x和y轴的方向，满足右手法则
通过定义了x轴的方向，我们可以方便地确定每个关节之间的相对方位和运动关系。

同时，通过标准DH方法可以建立一系列齐次变换矩阵，用于描述整个机器人的位姿和运动。

需要注意的是，标准DH方法只是一种约定和描述机器人运动学的方法，x轴方向并不一定要按照特定的规则进行定义，具体的定义方式可能因机器人模型的不同而有所变化。

因此，在实际应用中，需要根据具体的机器人模型和需要进行适当的调整。

机器人dh参数法机器人dh参数法是机器人运动学中一种常见的时空描述方式，它可将机器人末端执行器的位置转化为机器人每个关节的位置和姿态。

本文将分步骤介绍机器人dh参数法的相关内容。

一、机器人dh参数定义dh参数是一组约定的参数，它能够描述机器人的几何和动力学特征，包括机器人关节变量和机器人工具的链接参数。

其主要包括以下4个参数：1. d：表示沿z轴的偏移量，即关节的偏移量，它可以正表示z轴朝向末端执行器方向，也可以反表示z轴朝向基座的方向。

2. a：表示沿x轴的长度，即相对于前一个关节，在x方向上的位移。

3. \alpha：表示关节底座坐标系z轴与相邻关节坐标系z轴之间的夹角。

4. \theta：表示关节转角，即旋转的角度，相邻关节坐标系之间z轴的夹角。

以上参数一般用$[d, a, \alpha, \theta]$的四元组来表示其在坐标系之间的关系。

其中，d, a, $\alpha$和$\theta$都是与机器人结构有关的常数，称机器人dh参数。

二、机器人dh参数法建模通过dh参数法，可以将机器人末端执行器的位置和姿态表示为机器人每个关节的位置和姿态。

具体的建模方法包括以下步骤：1. 选择机器人的坐标系：假设机器人是n个绝对刚性结构（关节）的串联，以其中的第i个关节为起点构建一个本地坐标系O(i)。

在这个坐标系中，z(i)轴指向第i+1个关节，并沿着它的转动轴表达（即选择z轴朝向）；x(i)轴沿着相邻两关节在O(i-1)中的相交线表达，也就是按照右手定则来表达。

2. 建立坐标系之间的转换：通过四种关系参数(d, a, $\alpha$,$\theta$)来描述相邻两个稳定结构之间的坐标系转换。

3. 坐标系间的相互关系：每个坐标系以自己的z轴为法向量，画出x轴与其它坐标系z轴的夹角。

假定坐标系i沿着x轴转动角度$\theta_i$与坐标系i-1对齐。

4. 构建机构的位姿矩阵：通过定义好的坐标系和它们之间的转换关系，可以构建机器人的位姿矩阵。

六轴机械臂逆运动学原理及仿真设计一、引言机械臂是一种能够模拟人类手臂运动的机械装置，广泛应用于工业自动化、医疗手术、物流等领域。

其中，六轴机械臂是一种常见的机械臂类型，具有较高的灵活性和精度。

本文将介绍六轴机械臂的逆运动学原理以及仿真设计。

二、六轴机械臂逆运动学原理逆运动学是指已知机械臂末端位置和姿态，求解各个关节角度的过程。

对于六轴机械臂而言，其逆运动学原理可以通过以下步骤进行求解：1. 建立坐标系首先，需要建立机械臂的坐标系。

对于六轴机械臂而言，通常采用DH（Denavit-Hartenber g）坐标系建立方法。

该方法通过定义关节坐标系和连杆坐标系之间的转换关系，将机械臂的运动描述为一系列的旋转和平移运动。

2. 建立正运动学模型根据机械臂的几何参数和DH坐标系的定义，可以建立机械臂的正运动学模型。

正运动学模型可以将关节角度转化为末端位置和姿态的描述，即由关节角度求解末端位置和姿态。

3. 求解逆运动学问题已知末端位置和姿态，需要求解各个关节角度。

逆运动学问题通常存在多解性，即可以有多组关节角度满足末端位置和姿态的要求。

求解逆运动学问题的方法有数值解法和解析解法两种。

数值解法通常采用迭代的方式，通过不断调整关节角度的初始值，使得末端位置和姿态逼近目标值。

常用的数值解法有牛顿-拉夫逊法（Newton-Raphson）和雅可比转置法（Jacobi an transpose）等。

解析解法则通过数学推导直接求解关节角度的表达式。

解析解法的优点是计算速度快，但对于复杂的机械臂结构和运动约束较多的情况，解析解法可能无法求解。

三、六轴机械臂仿真设计六轴机械臂的仿真设计可以通过计算机软件进行，常用的仿真软件有MATLAB、SolidWor ks和ROS等。

以下是一种基于ROS的六轴机械臂仿真设计流程：1. 建立机械臂模型在ROS中，可以通过URDF（Unified Robot Description Format）文件来描述机械臂的几何参数和运动学信息。