向量的点乘和叉乘以及几何意义

向量相乘几何意义1. 向量的乘法的几何意义：向量的乘法，即叉乘，就是两个向量的矢量积，也叫向量积、叉乘。

它表示在三维空间中两个向量的交叉影响。

叉乘的计算结果是一个新的向量，它与原来两个向量不共线（垂直），新向量指向与两个向量夹角关系最小的方向，新向量的模大小取决于原来向量的模和夹角。

2. 投影乘法几何意义：向量投影乘法是为了了解两个向量之间的相似性，它是把一个向量投影到另一个向量上，然后求出两个向量的内积，它描述的是两个向量的大小和方向的关系。

三维空间中的向量投影，得出的结果是一个垂直于另一向量的向量，可以表示为一个实值，表示投影后的向量的模长。

3. 向量的点乘几何意义：向量的点乘就是两个向量的点积，也叫内积。

它表示对两个向量之间的角度。

如果两个向量夹角为90°，说明他们是正交，点乘结果为0。

另外，点乘结果大于0，说明他们夹角小于90°；点乘结果小于0，则说明他们夹角大于90°。

4. 向量的乘法的应用：（1）在几何中，向量的乘法可以用来求出三角形的重心。

（2）在物理学中，向量的乘法可以用来求出力矩，从而了解力和位移之间的关系。

（3）在几何中，向量投影乘法可以用来求出过某点的投影线和一条向量的投影。

（4）在几何中，可以用点乘乘法求出两个向量之间的夹角，求出相交后三角形的重心，也可以用来求出向量的长度。

（5）在数学中，向量的乘法可以用来求解线性方程组的解。

（6）在统计学中，可以通过向量的乘法和投影乘法来求出最小二乘回归。

（7）在仿真中，可以通过向量的乘法来求出任意天体运行的轨迹。

向量的点乘与叉乘的几何意义与计算方法向量是数学中的重要概念，它在几何学、物理学和工程学等领域中都有广泛的应用。

在向量运算中，点乘和叉乘是两个常见且重要的运算。

本文将探讨向量的点乘和叉乘的几何意义和计算方法。

一、向量的点乘向量的点乘，也称为内积或数量积，是两个向量之间的一种运算。

点乘的结果是一个标量，用于衡量两个向量之间的相似程度。

点乘的计算方法如下：设有两个向量A和B，A的坐标表示为(Ax, Ay, Az)，B的坐标表示为(Bx, By, Bz)。

则A和B的点乘结果为：A·B = Ax * Bx + Ay * By + Az * Bz点乘的几何意义是通过计算两个向量之间的夹角来衡量它们的相似程度。

具体来说，点乘的结果等于两个向量的模长乘积与它们夹角的余弦值的乘积。

如果两个向量夹角为锐角，则点乘结果为正值；如果夹角为钝角，则点乘结果为负值；如果夹角为直角，则点乘结果为零。

点乘还有其他重要的应用，例如计算向量的投影。

通过点乘可以得到一个向量在另一个向量上的投影长度。

这在物理学中常用于计算力的分解和合成。

二、向量的叉乘向量的叉乘，也称为外积或向量积，是两个向量之间的一种运算。

叉乘的结果是一个新的向量，它与原来的两个向量都垂直，并且符合右手定则。

叉乘的计算方法如下：设有两个向量A和B，A的坐标表示为(Ax, Ay, Az)，B的坐标表示为(Bx, By, Bz)。

则A和B的叉乘结果为：A×B = (Ay * Bz - Az * By, Az * Bx - Ax * Bz, Ax * By - Ay * Bx)叉乘的几何意义是通过计算两个向量所构成的平行四边形的面积来衡量它们的相似程度。

具体来说，叉乘的结果的模长等于两个向量所构成平行四边形的面积，方向则由右手定则确定。

叉乘在几何学和物理学中有广泛的应用。

例如，在计算力矩时，可以利用叉乘来求解力和力臂之间的关系。

此外，叉乘还可以用于计算平面的法向量，用于求解直线和平面的交点等。

向量的点乘和叉乘以及几何意义|b|cosθ我试着证明为什么会是这样（为了能让大家看的方便，我将向量标为蓝色，具体长度标为红色）：定义向量c=a2abcos(θ)(这里的a,b,c全部都是每一边的具体长度)根据定义我们可以推导出cc=c(有兴趣的朋友可以去试着推导一下)所以：cc=aa+bb-2abcos(θ)因为向量的点乘满足分配率：a(b+c)=ab+acc=ab)(a2ab+bb)(aa2abcos(q)约掉aa=a,bb=b;-2ab= -2abcos(θ)ab=abcos(θ)因为a=|a|所以ab=|a| |b|cosθ跟据这个公式，我们能拿到两个向量之间的夹角，这对于判断两个向量是否同一方向，是否正交(也就是垂直)，很有用处。

具体判断如下：ab>0方向基本相同，夹角在0到90之间ab=0正交ab<0方向基本相反，夹角在90到180之间所以，点乘的几何意义和用处就是计算两个向量之间的夹角，以及在某一方向上的投影。

至于为什么要判断两个向量是否方向一致，这在3D中很有用处。

比如：3D技术中的光栅化（光栅化的任务是为了绘制每个三角形单元，如何计算构成三角形单元的每个像素的颜色值）过程中，我们可以根据两个面的法向量的点乘判断两个面是否处于同一面，如果不是，那么只要光栅化其中需要显示出来的一面，而另一面我们就不用光栅化它（因为我们根本看不到被遮住的面），这样就节省了很多很多计算，能加快效率。

向量的叉乘(也叫做叉积)为什么是这样，上面已经说过，规定就这样。

同样，我们给出叉乘的几何解释：在3维几何中，我们可以一眼看出来，叉乘的结果也是一个向量，而且这个向量不是一般的向量，而是大名鼎鼎的"法向量"，3D技术中法向量有多重要我就不吹了，反正是个VIP概念。

在2维集合中，axb等于由向量组成的平行四边形的面积（证明很简单，你们可以自己试着证明）总之：向量的叉积最重要的应用就是创建垂直于平面，三角形，或者多边形的向量。

向量点乘、叉乘的定义及几何意义
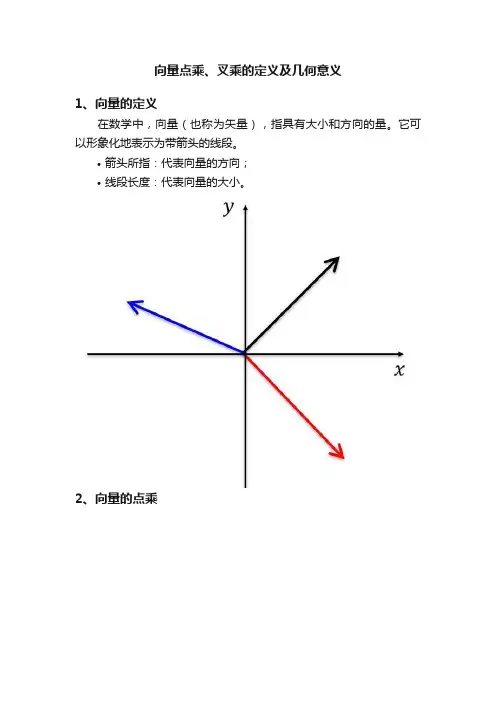
1、向量的定义
在数学中，向量（也称为矢量），指具有大小和方向的量。

它可以形象化地表示为带箭头的线段。

•箭头所指：代表向量的方向；
•线段长度：代表向量的大小。

2、向量的点乘
•向量点乘的数学定义：
•向量点乘的几何意义：
向量的点乘可以用来计算两个向量之间的夹角，进一步判断这两个向量是否正交（垂直）等方向关系。

同时，还可以用来计算一个向量在另一个向量方向上的投影长度。

3、向量的叉乘
•向量叉乘的数学定义：
•向量叉乘的几何定义：
叉乘的运算结果是一个向量而不是一个标量，上述结果是它的模，
向量C的方向与A，B所在的平面垂直，方向用“右手法则”判断。

判断方法如下：
•右手手掌张开，四指并拢，大拇指垂直于四指指向的方向；
•伸出右手，四指弯曲，四指与A旋转到B方向一致，那么大拇指指向为C向量的方向。

在二维空间中，叉乘还有另外一个几何意义就是：叉积等于由向量A和向量B构成的平行四边形的面积。

所谓点乘（也常称作内积），数学定义如下：点乘只是表达这个结果的一种方式，符号不重要，叫法也不重要，我可以叫点乘，内积，也可以叫"相乘"，定义"#"字符代替“·” 符号都可以，只是人们约束习惯这么这么写，那我们就也都这么写。

而且，也不要纠结为什么是这么定义，没有为什么，人们就是这么“龟腚”这个公式的，我们要研究的是这个规定到底能干嘛？有啥具体意义？a.点乘的具体几何意义：根据公式，我们可以得出a·b=|a| |b|cosθ我试着证明为什么会是这样（为了能让大家看的方便，我将向量标为蓝色，具体长度标为红色）：定义向量c=a - b这样就形成了一个封闭的三角形，c向量为他的第三边由于余弦定理我们可以知道c² =a² +b² - 2ab cos(θ) (这里的a,b,c全部都是每一边的具体长度)根据定义我们可以推导出c·c=c²(有兴趣的朋友可以去试着推导一下)所以：c·c=a·a+b·b- 2ab cos(θ)因为向量的点乘满足分配率：a·(b+c)=a·b+a·cc=a - bc·c=(a -b)·(a - b)c·c=(a·a-2a·b+b·b)(a·a - 2a·b + b·b)=a²+b²- 2ab cos(q)约掉a·a=a²,b·b=b²;-2a·b= -2ab cos(θ)a·b=ab cos(θ)因为a=|a|所以a·b=|a| |b|cosθ跟据这个公式，我们能拿到两个向量之间的夹角，这对于判断两个向量是否同一方向，是否正交(也就是垂直)，很有用处。

【最新整理，下载后即可编辑】概念向量是由n个实数组成的一个n行1列（n*1）或一个1行n列（1*n）的有序数组；向量的点乘，也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。

点乘公式对于向量a和向量b：a和b的点积公式为：要求一维向量a和向量b的行列数相同。

点乘几何意义点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影，有公式：推导过程如下，首先看一下向量组成：定义向量：根据三角形余弦定理有：根据关系c=a-b（a、b、c均为向量）有：即：向量a，b的长度都是可以计算的已知量，从而有a和b间的夹角θ：根据这个公式就可以计算向量a和向量b之间的夹角。

从而就可以进一步判断这两个向量是否是同一方向，是否正交(也就是垂直)等方向关系，具体对应关系为：a·b>0 方向基本相同，夹角在0°到90°之间a·b=0 正交，相互垂直a·b<0 方向基本相反，夹角在90°到180°之间叉乘公式两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量。

并且两个向量的叉积与这两个向量组成的坐标平面垂直。

对于向量a和向量b：a和b的叉乘公式为：其中：根据i、j、k间关系，有：叉乘几何意义在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。

如下图所示：在二维空间中，叉乘还有另外一个几何意义就是：aXb等于由向量a和向量b构成的平行四边形的面积。

向量的点乘和叉乘以及几何意义一、向量的点乘1.定义：向量的点乘，又称为数量积或内积，是两个向量之间的一种乘法运算。

对于两个n维向量a和b，它们的点乘定义为a·b = ，a，b，cosθ，其中，a，和，b，分别表示向量a和b的模的大小，θ表示a和b之间的夹角。

2.计算方法：（1）向量坐标表示计算方法：如果a=(a₁,a₂,...,aₙ)和b=(b₁,b₂,...,bₙ)是两个n维向量，它们的点乘可以用下面的公式来计算：a·b=a₁b₁+a₂b₂+...+aₙbₙ。

（2）向量模和夹角计算方法：如果，a，和，b，分别是向量a和b的模的大小，θ是向量a和b之间的夹角，则向量的点乘可以用下面的公式来计算：a·b = ，a，b，cosθ。

3.几何意义：（1）判断两个向量是否相互垂直：如果两个向量的点乘结果为0，即a·b=0，那么这两个向量相互垂直。

（2）计算向量在一些方向上的投影：如果向量a的模为，a，θ是a与b之间的夹角，那么向量a在向量b的方向上的投影长度为，a，cosθ。

（3）计算两个向量之间的夹角：如果向量a和b的点乘为a·b = ，a，b，cosθ，那么两个向量之间的夹角θ可以通过反余弦函数计算：θ = arccos(a·b / ，a，b，)。

二、向量的叉乘1.定义：向量的叉乘，又称为向量积或外积，是两个三维向量之间的一种乘法运算。

对于两个三维向量a和b，它们的叉乘定义为a×b = ，a，b，sinθn，其中，a，和，b，分别表示向量a和b的模的大小，θ表示a和b之间的夹角，n表示与a和b所在平面垂直的单位向量。

2.计算方法：向量的叉乘的计算可以利用行列式的方法进行计算：a×b=，ijk，，a₁a₂a₃，，b₁b₂b₃，其中，ijk，表示三个单位向量i、j、k所组成的行列式，a₁、a₂、a₃和b₁、b₂、b₃分别表示向量a和b的坐标。

向量的点乘和叉乘以及几何意义1.点乘（内积）对于两个n维向量A和B，其点乘表示为A·B，计算方式为：A·B=A1B1+A2B2+···+AnBn其中，A1,A2,...,An和B1,B2,...,Bn分别是向量A和B的各个分量。

点乘的几何意义：-点乘的结果是一个实数，代表两个向量之间的数量关系。

-点乘可以用来判断两个向量之间的夹角。

具体而言，当两个向量夹角为锐角时，点乘结果为正；夹角为直角时，点乘结果为零；夹角为钝角时，点乘结果为负。

-点乘可以用来判断向量间的垂直关系。

两个向量的点乘结果为零，则表示两个向量相互垂直。

点乘的应用：-计算向量的模长：对于一个n维向量A，其模长的平方等于向量自身与自身的点乘，也即A·A=A1^2+A2^2+···+An^2-计算向量投影：点乘可以将向量A在向量B上的投影表示为A·B/，B，其中，B，表示向量B的模长。

-判断向量的方向：当两个向量夹角为锐角时，点乘结果为正；当夹角为钝角时，点乘结果为负。

通过点乘可以判断两个向量之间的相对方向。

2.叉乘（外积）向量的叉乘，也称为外积或向量积，是一种二元运算，结果为一个新的向量，其方向垂直于原来的两个向量，大小等于两个向量构成的平行四边形的面积。

具体的叉乘定义如下：对于两个三维向量A和B，其叉乘表示为A×B，计算方式为：A×B=(A2B3-A3B2,A3B1-A1B3,A1B2-A2B1)叉乘的几何意义：-叉乘的结果是一个新的向量，它垂直于原来的两个向量，并且方向符合右手螺旋法则。

具体来说，如果右手的四指沿着向量A的方向伸出，再让手指旋转到向量B的方向时，大拇指的方向就是向量A×B的方向。

-叉乘的大小等于两个向量构成的平行四边形的面积。

这意味着当两个向量平行时，叉乘的结果为零；当两个向量互相垂直时，叉乘的结果为两个向量的模长的乘积。

向量点乘：（内积）点乘（Dot Product）的结果是点积，又称数量积或标量积（Scalar Product）。

在空间中有两个向量： \vec a=(x_1,y_1,z_1) ， \vecb=(x_2,y_2,z_2)， \vec a 与 \vec b之间夹角为 \theta。

从代数角度看，点积是对两个向量对应位置上的值相乘再相加的操作，其结果即为点积。

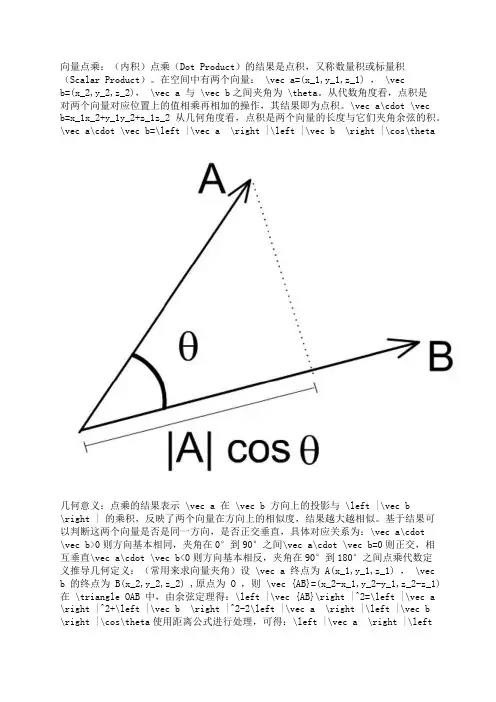
\vec a\cdot \vecb=x_1x_2+y_1y_2+z_1z_2从几何角度看，点积是两个向量的长度与它们夹角余弦的积。

\vec a\cdot \vec b=\left |\vec a \right |\left |\vec b \right |\cos\theta几何意义：点乘的结果表示 \vec a 在 \vec b 方向上的投影与 \left |\vec b\right | 的乘积，反映了两个向量在方向上的相似度，结果越大越相似。

基于结果可以判断这两个向量是否是同一方向，是否正交垂直，具体对应关系为：\vec a\cdot\vec b>0则方向基本相同，夹角在0°到90°之间\vec a\cdot \vec b=0则正交，相互垂直\vec a\cdot \vec b<0则方向基本相反，夹角在90°到180°之间点乘代数定义推导几何定义：（常用来求向量夹角）设 \vec a 终点为 A(x_1,y_1,z_1) ， \vec b 的终点为B(x_2,y_2,z_2) ,原点为 O ，则 \vec {AB}=(x_2-x_1,y_2-y_1,z_2-z_1)在 \triangle OAB 中，由余弦定理得：\left |\vec {AB}\right |^2=\left |\vec a \right |^2+\left |\vec b \right |^2-2\left |\vec a \right |\left |\vec b \right |\cos\theta使用距离公式进行处理，可得：\left |\vec a \right |\left|\vec b \right |\cos\theta=\frac {x_1^2+y_1^2+z_1^2+x_2^2+y_2^2+z_2^2-[(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2]}{2}去括号后合并，可得：\left |\vec a \right |\left |\vec b \right |\cos\theta=x_1x_2+y_1y_2+z_1z_2=\vec a\cdot \vec b根据上面的工式可计算 \vec a 与 \vec b 之间的夹角： \theta=\arccos (\frac {\vec a\cdot\vec b} {\left |\vec a \right |\left |\vec b \right |})向量叉乘：（外积）叉乘（Cross Product）又称向量积（Vector Product）。

向量的点乘和叉乘以及几何意义向量是代表大小和方向的量，可以用来描述物理量、力、速度、位移等。

在向量运算中，点乘和叉乘是两个重要的操作。

它们有着不同的定义和几何意义。

一、点乘（内积）：1. 定义：对于给定的两个向量a和b，它们的点乘定义为：a·b = ，a，b，cosθ，其中，a，和，b，分别表示向量a和b的长度，θ表示夹角。

2.计算：点乘可以通过将对应的分量相乘再相加得到。

假设a=(a1,a2,a3)和b=(b1,b2,b3)，那么a·b=a1b1+a2b2+a3b33.几何意义：-点乘的结果是一个标量，表示向量a在向量b上的投影的长度乘以b的模长。

可以通过这个特性计算物体的投影、距离等问题。

-点乘的结果a·b=0时，表示a与b垂直或其中至少有一个是零向量。

-点乘的结果a·b>0时，表示a和b之间夹角小于90°，它们的方向相似。

-点乘的结果a·b<0时，表示a和b之间夹角大于90°，它们的方向相反。

4.应用：-判断两个向量的夹角大小。

-判断向量是否垂直。

-计算工作和力的做功。

-判断两个向量的方向。

二、叉乘（外积）：1. 定义：对于给定的两个向量a和b，它们的叉乘定义为：a×b = ，a，b，sinθn，其中，a，和，b，分别表示向量a和b的长度，θ表示夹角，n表示与a和b所在平面垂直的单位向量。

2.计算：叉乘可以通过行列式的形式计算。

假设a=(a1,a2,a3)和b=(b1,b2,b3)，那么a×b=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)。

3.几何意义：- 叉乘的结果是一个向量，它垂直于向量a和b所在的平面，其大小等于ab所围成的平行四边形的面积。

-叉乘的方向满足右手定则，即右手四指指向a，然后弯曲的拇指指向b，拇指的方向就是叉乘的方向。

-叉乘的结果a×b=0时，表示a和b平行或其中至少有一个是零向量。

向量点乘和叉乘概念及几何意义解读向量点乘和叉乘是向量拓展运算的两种常见形式。

它们不仅在数学上有重要的应用，同时在几何学中也具有重要的几何意义。

1.向量点乘：向量点乘又被称为内积，用符号"·"表示。

对于两个向量A和B，它们的点乘结果可以用如下公式表示：A·B = ，A，× ，B，× cosθ其中，A，和，B，表示向量的模(长度)，θ表示A和B之间的夹角。

几何意义：向量点乘的几何意义在于可以刻画两个向量之间的几何关系。

根据向量点乘的性质，可得到以下结论：a)如果A·B=0，说明两个向量A和B正交(垂直于彼此)。

b)如果A·B>0，说明夹角θ为锐角，即两个向量趋于同一方向。

c)如果A·B<0，说明夹角θ为钝角，即两个向量趋于相反方向。

另外，向量点乘可用来计算一些向量在另一个向量方向上的投影。

具体而言，向量A在B方向上的投影等于(A·B)/，B，×B。

2.向量叉乘：向量叉乘又被称为外积或向量积，用符号"×"表示。

对于两个向量A和B，它们的叉乘结果可以用如下公式表示：A×B = ，A，× ，B，× sinθ× n其中，A，和，B，表示向量的模，θ表示A和B之间的夹角，n表示垂直于A和B所在平面的单位向量。

几何意义：向量叉乘的几何意义在于可以刻画两个向量之间的几何关系。

根据向量叉乘的性质，可得到以下结论：a)向量叉乘的结果是与A和B都垂直的向量。

这个垂直向量的方向可以通过右手法则确定，即右手的四指指向A，然后弯曲指向B的拇指所指的方向。

b)向量叉乘的模等于以A和B所在平面为底面的平行四边形的面积。

c)如果A和B共线，则它们的向量叉乘结果为零。

在几何学中，向量叉乘被广泛应用于描述平面和空间中的曲面、法线、旋转等概念。

例如，在三维空间中，计算离散点的法向量时常用到向量叉乘。

向量点乘和叉乘的意义
1、向量点乘意义：可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影。

2、向量叉乘意义：在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。

3、两者区别：
（1）向量点乘结果是标量，是两个向量在一个方向的累计结果，结果只保留大小属性，抹去方向属性，就相等于降维；
（2）向量叉乘，是这这两个向量平面上，垂直生成新的向量，大小是两个向量构成四边形的面积。

相等于生维。

这是运算所需要，向量加和减都是在同一纬空间操作的，如果要想实现维度的变化就要在向量的乘法做出定义。

点乘和叉乘
点乘是向量的内积，叉乘是向量的外积。

点乘，也叫数量积。

结果是一个向量在另一个向量方向上投影的长度，是一个标量。

顾名思义，求下来的结果是一个数。

叉乘，也叫向量积。

结果是一个和已有两个向量都垂直的向量。

求下
来的结果是一个向量。

扩展资料：
线性变换中点积的意义：
根据点积的代数公式：a·b=a1b1+a2b2+……+anbn，假设a为给定权
重向量，b为特征向量，则a·b其实为一种线性组合，函数F（a·b）则
可以构建一个基于a·b+c = 0 （c为偏移）的其中一超平面的线性分类器，F是个简单函数，会将超过一定阈值的值对应到第一类，其它的值对
应到第二类。

向量的点积与它们夹角的余弦成正比，因此在聚光灯的效果计算中，
可以根据点积来得到光照效果，如果点积越大，说明夹角越小，则物体离
光照的轴线越近，光照越强。

点乘和叉乘的物理意义
点乘和叉乘是向量运算中常见的两种运算，它们在物理中有着重要的应用。

点乘，也称为数量积或内积，是两个向量的标量积。

其结果是两个向量之间的夹角的余弦值与两个向量长度之积的乘积。

点乘的意义在于，它可以用来计算两个向量之间的投影。

在力学中，点乘可以用来计算两个力的相对方向和大小，从而确定它们在特定方向上的作用效果。

叉乘，也称为向量积或外积，是两个向量的叉积。

其结果是一个向量，方向垂直于两个向量所在的平面，大小等于两个向量之间夹角所组成的平行四边形的面积。

叉乘的意义在于，它可以用来计算向量之间的叉积积，从而得出向量之间的垂直关系。

在力学中，叉乘可以用来计算力矩，即力在物体上产生的旋转效果，以及电磁感应中的磁通量和电场强度之间的关系。

向量的点乘和叉乘向量是数学中非常重要的概念之一。

它可以表示空间中的一条线段并且具有有向性。

在向量的运算中，点乘和叉乘是两个非常关键的操作。

本文将深入探讨向量的点乘和叉乘。

一、向量的点乘向量的点乘也叫做内积，它是一个标量的运算。

设两个向量a 和b，它们的点乘可以表示为a·b。

点乘的计算方式如下：a·b=|a||b|cosθ，其中|a|表示向量a的模长，|b|表示向量b的模长，θ表示a、b两向量的夹角。

可以看出，点乘的结果是一个标量，它等于两向量模长之积再乘上它们夹角的余弦值。

点乘的作用非常广泛，它可以用于计算两个向量之间的夹角、向量在某个方向上的投影以及向量在某个方向上的大小等。

在物理学中，向量的点乘还可以用于计算功和能量。

点乘还有一个很重要的特性，即两向量的点乘等于其中一个向量在另一个向量方向上的投影的长度与它们模长之积的积。

二、向量的叉乘向量的叉乘也叫做外积，它是一个向量的运算。

设两个向量a 和b，它们的叉积可以表示为a×b。

叉乘的计算方式如下：a×b=|a||b|sinθn，其中|a|表示向量a的模长，|b|表示向量b的模长，θ表示a、b两向量的夹角，n表示垂直于a、b两向量所在平面的单位向量。

可以看出，叉乘的结果是一个向量，它的方向垂直于a、b两向量所在平面，并且遵循右手法则。

即将右手放置在a、b两向量所在的平面上，让拇指指向a，食指指向b，中指的方向就是向量a×b的方向。

叉乘还有一个很重要的性质，即两个向量的叉乘的模长等于两个向量所围成的平行四边形的面积。

叉乘在实际应用中也有很多的作用。

在物理学中，向量的叉乘可以用于计算电磁场的旋度。

在计算机图形学中，叉乘可以用于计算法向量等。

总结向量的点乘和叉乘是向量运算中最为基本且重要的概念之一。

点乘是一个标量的运算，而叉乘是一个向量的运算。

它们都有着广泛的应用，并且在数学、物理学、工程学、计算机图形学等领域都扮演着重要的角色。

物理中点乘和叉乘的区别在物理学和数学中，向量运算扮演着重要的角色。

点乘和叉乘作为两种基本的向量运算方式，在描述物体运动和力的作用时具有不同的意义和用途。

本文将详细解析点乘和叉乘的区别。

一、定义及表达式1.点乘（又称标量乘积或数量积）：点乘是指两个向量在数量上的乘积，结果为一个标量（即一个数值）。

对于三维空间中的两个向量A（a1, a2, a3）和B（b1, b2, b3），点乘的表达式为：A·B = a1b1 + a2b2 + a3b32.叉乘（又称向量积或叉积）：叉乘是指两个向量在方向上的乘积，结果为一个向量。

对于三维空间中的两个向量A和B，叉乘的表达式为：A×B = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)二、性质及特点1.点乘：- 结果为标量，只描述大小，无方向；- 交换律：A·B = B·A；- 适用于描述力的大小、能量转换等。

2.叉乘：- 结果为向量，既有大小也有方向；- 反交换律：A×B = -B×A；- 适用于描述力矩、角速度等。

三、应用场景1.点乘：- 动力学中，力F和位移S的点乘表示力所做的功：W = F·S；- 电磁学中，电场E和电荷q的点乘表示电场对电荷的作用力：F = qE。

2.叉乘：- 刚体动力学中，力F和力臂r的叉乘表示力矩M：M = F×r；- 流体力学中，速度v和旋度ω的叉乘表示涡量。

四、总结点乘和叉乘在物理中的运用有着明显的区别，主要体现在结果类型、运算性质和应用场景等方面。

了解这两种运算的区别和联系，有助于我们更好地理解物理现象和解决实际问题。

了解向量的叉乘与点乘向量是数学中的重要概念，广泛应用于物理、计算机科学等领域。

向量的运算中，叉乘和点乘是两个基本操作，本文将介绍向量的叉乘和点乘的概念、性质以及应用。

一、向量的概念向量是指具有大小和方向的量。

通常用箭头表示，箭头的长度代表向量的大小，箭头的方向代表向量的方向。

向量可以用有序数组表示，也可以用坐标表示。

有序数组表示时，向量常用小写字母加粗表示，比如a；坐标表示时，则将向量与其他向量关联，比如OA。

二、向量的点乘点乘也称为内积或数量积，是两个向量之间的一种运算。

给定两个向量a和b，它们的点乘表示为a·b，其计算方式为将两个向量对应分量相乘再相加。

数学上，设a=(a1, a2, a3)和b=(b1, b2, b3)是两个三维向量，则a·b=a1b1+a2b2+a3b3。

如果向量是二维的，则点乘的计算方式类似。

点乘的运算可以应用于求向量之间的夹角，有如下公式：cosθ = (a·b) / (|a| * |b|)其中θ表示向量a和b之间的夹角，|a|表示向量a的长度，|b|表示向量b的长度。

三、向量的叉乘叉乘也称为外积或向量积，是两个向量之间的一种运算。

给定两个向量a和b，它们的叉乘表示为a×b，其计算方式为：a×b = |a| |b| sinθ n其中|a|和|b|分别表示向量a和b的长度，θ表示向量a和b之间的夹角，n是一个垂直于a和b的单位向量。

由于叉乘的结果是一个新的向量，因此它的方向垂直于a和b所在的平面。

叉乘的运算可以应用于求向量之间的面积和方向，有如下公式：|a×b| = |a| |b| sinθ其中|a×b|表示叉乘的结果向量的长度，即向量a和b所张成的平行四边形的面积。

四、向量叉乘和点乘的应用1. 几何应用向量的叉乘在几何学中有广泛的应用。

例如，通过叉乘可以求得两个向量所张成的平面的法向量，从而帮助解决平面几何中的一些问题。