深圳西丽湖世纪星学校数学有理数单元培优测试卷

一、选择题1．若12a = ，3b =，且0ab <，则+a b 的值为（ ）A ．52B ．52-C ．25±D ．52±2．2--的相反数是（ ） A ．12-B ．2-C ．12D ．23．在日历纵列上圈出了三个数，算出它们的和，其中正确的一个是（ ） A ．28 B ．34 C ．45 D ．75 4．-1+2-3+4-5+6+…-2011+2012的值等于 A ．1B ．-1C ．2012D ．10065．下列各组数中，互为相反数的是（ ）A ．（﹣3）2和﹣32B ．（﹣3）2和32C ．（﹣2）3和﹣23D ．|﹣2|3和|﹣23|6．若a ，b 互为相反数，则下面四个等式中一定成立的是（ ） A ．a+b=0 B ．a+b=1C ．|a|+|b|=0D ．|a|+b=0 7．下列关系一定成立的是（ ） A ．若|a|＝|b|，则a ＝b B ．若|a|＝b ，则a ＝b C ．若|a|＝﹣b ，则a ＝bD ．若a ＝﹣b ，则|a|＝|b|8．如果a ，b ，c 为非零有理数且a + b + c = 0，那么a b c abc a b c abc+++的所有可能的值为（ A ．0B ．1或- 1C ．2或- 2D ．0或- 29．2020年5月7日，世卫组织公布中国以外新冠确诊病例约为3504000例，把“3504000”用科学记数法表示正确的是（ ） A ．3504×103B ．3.504×106C ．3.5×106D ．3.504×10710．下列四个式子，正确的是（ ） ①33.834⎛⎫->-+ ⎪⎝⎭；②3345⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭；③ 2.5 2.5->-；④125523⎛⎫-->+ ⎪⎝⎭． A ．③④B ．①C ．①②D ．②③11．下列说法中正确的是（ ） A ．a -表示的数一定是负数 B ．a -表示的数一定是正数 C ．a -表示的数一定是正数或负数 D ．a -可以表示任何有理数12．当A 地高于海平面152米时，记作“海拔+152米”，那么B 地低于海平面23米时，记作（ ） A ．海拔23米B ．海拔﹣23米C ．海拔175米D ．海拔129米13．某市11月4日至7日天气预报的最高气温与最低气温如表： 日期11月4日11月5日 11月6日 11月7日 最高气温（℃） 19 1220 9 最低气温（℃） 43-45其中温差最大的一天是（ ） A ．11月4日B ．11月5日C ．11月6日D ．11月7日14．下面说法中正确的是 （ ） A ．两数之和为正，则两数均为正 B ．两数之和为负，则两数均为负 C ．两数之和为0，则这两数互为相反数D ．两数之和一定大于每一个加数15．若2020M M +-＝+，则M 一定是（ ） A ．任意一个有理数B ．任意一个非负数C ．任意一个非正数D ．任意一个负数二、填空题16．一条数轴上有点A 、B 、C ，其中点A 、B 表示的数分别是16-、9，现以点C 为折点，将放轴向右对折，若点A 对应的点A '落在点B 的右边，若3A B '=，则C 点表示的数是______．17．在数轴上，若点A 与表示3-的点相距6个单位,则点A 表示的数是__________． 18．数轴上表示 1 的点和表示﹣2 的点的距离是_____．19．已知a 是7的相反数，b 比a 的相反数大3，则b 比a 大____．20．我国“杂交水稻之父”袁隆平主持研究的某种超级杂交稻平均亩产820千克，某地今年计划栽种这种超级杂交稻30万亩，预计今年这种超级杂交稻的产量_____千克（用科学记数法表示） 21．填空： 3÷3＝____3×13＝____ (－12)÷(－2)＝____(－12)×12⎛⎫-⎪⎝⎭＝____ (－9)÷12＝____ (－9)×2＝____22．计算－32＋5－8×（－2）时，应该先算_____，再算_____，最后算_____．正确的结果为_____．23．某商店营业员每月的基本工资为4000元，奖金制度是每月完成规定指标10000元营业额，发奖金300元；若营业额超过规定指标，另奖超额部分营业额的5%．该商店的一名营业员九月份完成营业额13200元，则他九月份的收入为________元．24．点A 表示数轴上的一个点，将点A 向右移动10个单位长度，再向左移动8个单位长度，终点恰好是原点，则点A 到原点的距离为______． 25．比较大小：364--_____________()6.25--． 26．(1)圆周率π＝3.141 592 6…，取近似值3.142，是精确到____位； (2)近似数2.428×105精确到___位；(3)用四舍五入法把3.141 592 6精确到百分位是____，近似数3.0×106精确到____位．三、解答题27．阅读下列材料：(0)0(0)(0)x x x x x x >⎧⎪==⎨⎪-<⎩，即当0x <时，1x x x x ==--．用这个结论可以解决下面问题：（1）已知a ，b 是有理数，当0ab ≠时，求a ba b+的值； （2）已知a ，b ，c 是有理数，0a b c ++=，0abc <，求b c a c a ba b c+++++的值． 28．某路公交车从起点经过A ，B ，C ，D 站到达终点，一路上下乘客如下表所示．（用正数表示上车的人数，负数表示下车的人数））到终点下车还有多少 人；（2）车行驶在____站至___ 站之间时，车上的乘客最多；（3）若每人乘坐一站需买票0.5元，问该车出车一次能收入多少钱？列式计算． 29．计算：（1）()213433⎛⎫---+-+ ⎪⎝⎭； （2）()()202011232---+-+． 30．计算（1）28()5(0.4)5+----； （2）1571361236⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭； （3）2336()(2)()(6)575⨯---⨯-+-⨯； （4）42019213(20.2)(2)(1)5⎡⎤---+-÷⨯---⎢⎥⎣⎦；（5）24512.5()(0.1)(2)(2)10⎡⎤÷-⨯---+-⎣⎦．。

一、选择题1．已知数列{}n a 的前n 项和2n S n =，()1nn n b a =-则数列{}n b 的前n 项和n T 满足（ ） A ．()1nn T n =-⨯ B ．n T n =C ．n T n =-D ．,2,.n n n T n n ⎧=⎨-⎩为偶数，为奇数2．设等比数列{}n a 的前n 项和为n S ，若633S S =， 则96S S =（ ） A ．2B ．73C ．83D ．33．已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈的最小值为M ,若M ≤恒成立, 则实数m 的取值范围是（ ）A ．11,35⎡⎤-⎢⎥⎣⎦B ．11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C ．1,3⎡⎫-+∞⎪⎢⎣⎭D ．1,2⎡⎫-+∞⎪⎢⎣⎭4．已知,,a b R +∈且115a b a b+++=,则+a b 的取值范围是（ ） A ．[1,4]B ．[)2,+∞C ．(2,4)D ．(4,)+∞5．数列{}n a 为等比数列，若11a =，748a a =，数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ，则5(S = )A ．3116B ．158C ．7D ．316．设实数,x y 满足242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩，则1y x +的最大值是（ ）A ．-1B ．12C ．1D ．327．已知等比数列{}n a 的各项都是正数，且13213,,22a a a 成等差数列，则8967a a a a +=+ A ．6B ．7C ．8D ．98．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C=120°，c=√2a ，则 A ．a ＞b B ．a ＜bC ．a ＝bD ．a 与b 的大小关系不能确定9．已知正项等比数列{}n a 的公比为3，若229m n a a a =，则212m n+的最小值等于（ ） A ．1B ．12C ．34 D ．3210．已知等比数列{}n a 的各项均为正数，前n 项和为n S ，若26442,S 6a S a =-=，则5a =A ．4B ．10C ．16D ．3211．已知数列{a n }满足331log 1log ()n n a a n N +++=∈且2469a a a ++=，则15793log ()a a a ++的值是( )A ．－5B ．－15C ．5D ．1512．已知变量x , y 满足约束条件13230x x y x y ≥⎧⎪+≤⎨⎪--≤⎩，则2z x y =+的最小值为（ ）A ．1B ．2C ．3D ．613．已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧，给出以下结论：①3450a b -+>；②当0a >时，+a b 有最小值，无最大值；③221a b +>；④当0a >且1a ≠时，11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，正确的个数是（ ） A ．1B ．2C ．3D ．414．在ΔABC 中，A =60°，B =75°，BC =10，则AB = A ．5√2B ．10√2C ．5√6D ．10√6315．若变量x ，y 满足约束条件1358x y x x y ≥-⎧⎪≥⎨⎪+≤⎩，，，则2yz x =-的取值范围是（ ） A ．113⎡⎤-⎢⎥⎣⎦，B ．11115⎡⎤--⎢⎥⎣⎦，C ．111153⎡⎤-⎢⎥⎣⎦， D ．3153⎡⎤-⎢⎥⎣⎦，二、填空题16．已知lg lg 2x y +=，则11x y+的最小值是______. 17．《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为 升；18．已知n S 为数列{a n }的前n 项和，且22111n n n a a a ++-=-，21313S a =，则{a n }的首项的所有可能值为______19．设0a >，若对于任意满足8m n +=的正数m ，n ，都有1141a m n ++≤，则a 的取值范围是______.20．已知x y 、满足约束条件1{1,22x y x y x y +≥-≥--≤若目标函数()0,0z ax by a b =+>>的最大值为7，则34a b+的最小值为_______． 21．已知数列{}n a 满足51()1,62,6n n a n n a a n -⎧-+<⎪=⎨⎪≥⎩，若对任意*n N ∈都有1n n a a +>，则实数a 的取值范围是_________.22．已知a b c R ∈、、，c 为实常数，则不等式的性质“a b a c b c >⇐+>+”可以用一个函数在R 上的单调性来解析，这个函数的解析式是()f x =_________ 23．已知0a >，0b >，且31a b +=，则43a b+的最小值是_______. 24．已知等差数列{}n a 的公差为()d d 0≠，前n 项和为n S，且数列也为公差为d 的等差数列，则d =______．25．已知数列{}n a (*n ∈N )，若11a =，112nn n a a +⎛⎫+= ⎪⎝⎭，则2lim n n a →∞= ． 三、解答题26．若0,0a b >>,且11a b+=（1）求33+a b 的最小值；（2）是否存在,a b ，使得236a b +=？并说明理由.27．已知实数x 、y 满足6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩，若z ax y =+的最大值为39a +，最小值为33a -，求实数a 的取值范围.28．在ABC △中，内角,,A B C 所对的边分别为,,a b c ，且()sin 2sin 0b A a A C -+=． （1）求角A ；（2）若3a =，ABC △11b c +的值．29．已知锐角ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，且满足2sin 1cos A C B =-．（1）若2a =，c =b ；（2）若sin 4B =，a =b ． 30．等差数列{a n }的前n 项和为S n ，且3a =9，S 6=60． （I ）求数列{a n }的通项公式；（II ）若数列{b n }满足b n+1﹣b n =n a （n∈N +）且b 1=3，求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和T n ．【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．A 2．B 3．C 4．A 5．A 6．D 7．D 8．A 9．C 10．C 11．A 12．A13．B14．D15．A二、填空题16．【解析】由得：所以当且仅当时取等号故填17．【解析】试题分析：由题意可知解得所以考点：等差数列通项公式18．【解析】【分析】根据题意化简得利用式相加得到进而得到即可求解结果【详解】因为所以所以将以上各式相加得又所以解得或【点睛】本题主要考查了数列的递推关系式应用其中解答中利用数列的递推关系式得到关于数列首19．【解析】【分析】由题意结合均值不等式首先求得的最小值然后结合恒成立的条件得到关于a的不等式求解不等式即可确定实数a的取值范围【详解】由可得故：当且仅当即时等号成立故只需又则即则的取值范围是【点睛】在20．7【解析】试题分析：作出不等式表示的平面区域得到及其内部其中把目标函数转化为表示的斜率为截距为由于当截距最大时最大由图知当过时截距最大最大因此由于当且仅当时取等号考点：1线性规划的应用；2利21．【解析】【分析】由题若对于任意的都有可得解出即可得出【详解】∵若对任意都有∴∴解得故答案为【点睛】本题考查了数列与函数的单调性不等式的解法考查了推理能力与计算能力属于中档题22．【解析】【分析】构造函数通过讨论其单调性即解析不等式的性质【详解】函数是定义在上的单调增函数若则即即故答案为：【点睛】此题考查利用函数单调性解析不等式的性质利用常见函数的单调性结合不等式的特征即可求23．【解析】【分析】利用1的代换将求式子的最小值等价于求的最小值再利用基本不等式即可求得最小值【详解】因为等号成立当且仅当故答案为：【点睛】本题考查1的代换和基本不等式求最值考查转化与化归思想的运用求解24．【解析】【分析】表示出再表示出整理并观察等式列方程组即可求解【详解】等差数列的公差为前项和为设其首项为则=又数列也为公差为的等差数列首项为所以=即：整理得：上式对任意正整数n成立则解得：【点睛】本题25．【解析】【分析】由已知推导出=(=1+（）从而-=-由此能求出【详解】∵数列满足：∴（）+（）+……+（）=++……+==(∴=(；又+……+（）=1+++……+=1+=1+（）即=1+（）∴-=-三、解答题 26． 27． 28． 29． 30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．A 解析：A 【解析】 【分析】先根据2n S n =,求出数列{}n a 的通项公式,然后利用错位相减法求出{}n b 的前n 项和n T .【详解】解:∵2n S n =,∴当1n =时,111a S ==;当2n ≥时,()221121n n n a S S n n n -=-=--=-, 又当1n =时,11a =符合上式,∴21n a n =-, ∴()()()1121n nn n b a n =-=--,∴()()()()()123113151121nn T n =⨯-+⨯-+⨯-+⋅⋅⋅+--①,∴()()()()()2341113151121n n T n +-=⨯-+⨯-+⨯-+⋅⋅⋅+--②,①-②,得()()()()()()23412121111211n n n T n +⎡⎤=-+⨯-+-+-+⋅⋅⋅+---⨯-⎣⎦()()()()()()211111122112111n n n n n -+⎡⎤---⎣⎦=-+⨯--⨯-=---,∴()1nn T n =-,∴数列{}n b 的前n 项和()1nn T n =-.故选:A . 【点睛】本题考查了根据数列的前n 项和求通项公式和错位相减法求数列的前n 项和,考查了计算能力,属中档题.2．B解析：B 【解析】 【分析】首先由等比数列前n 项和公式列方程，并解得3q ，然后再次利用等比数列前n 项和公式，则求得答案． 【详解】设公比为q ，则616363313(1)1113(1)11a q S q q q a q S qq---===+=---， ∴32q =，∴93962611271123S q S q --===--． 故选：B ． 【点睛】本题考查等比数列前n 项和公式，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时也可以利用连续等长片断的和序列仍然成等比数列，进行求解.3．C解析：C 【解析】试题分析：直线()4x m y =-恒过定点(0,4)，当0m >时，约束条件()4{04y x y x m y ≤-≤≥-对应的可行域如图，则()OP OA R λλ-∈的最小值为0M =，满足M ≤，当0m =时，直线()4x m y =-与y 轴重合，平面区域()4{04y x y x m y ≤-≤≥-为图中y 轴右侧的阴影区域，则()OP OA R λλ-∈的最小值为0M =，满足2M ≤，当0m <时，由约束条件()4{04y x y x m y ≤-≤≥-表示的可行域如图，点P 与点B 重合时，()OP OA R λλ-∈的最小值为M OB =，联立{(4)y x x m y ==-，解得44(,)11m mB m m --，所以421m OB m =-，由4221m m ≤-，解得1135m -≤≤，所以103m -≤≤，综上所述，实数m 的取值范围是1,3⎡⎫-+∞⎪⎢⎣⎭，故选C.考点：简单的线性规划.【方法点晴】本题主要考查了二元一次不等式组所表示的平面区域、简单的线性规划求最值问题，着重考查了数形结合思想方法及分类讨论的数学思想方法的应用，关键是正确的理解题意，作出二元一次不等式组所表示的平面区域，转化为利用线性规划求解目标函数的最值，试题有一定的难度，属于难题.4．A解析：A 【解析】分析：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b +++=，可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭，化简整理即可得出. 详解：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b+++=，可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭， 化为()()2540a b a b +-++≤， 解得14a b ≤+≤， 则+a b 的取值范围是[]1,4. 故选：A.点睛：本题考查了基本不等式的性质、一元二次不等式的解法，考查了推理能力与计算能力，属于中档题.5．A解析：A 【解析】 【分析】先求等比数列通项公式，再根据等比数列求和公式求结果. 【详解】数列{}n a 为等比数列，11a =，748a a =，638q q ∴=，解得2q =， 1112n n n a a q --∴==，数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ， 55111111131211248161612S ⎛⎫⨯- ⎪⎝⎭∴=++++==-．故选A ． 【点睛】本题考查等比数列通项公式与求和公式，考查基本分析求解能力，属基础题.6．D解析：D 【解析】 【分析】由约束条件确定可行域，由1y x+的几何意义，即可行域内的动点与定点P （0，-1）连线的斜率求得答案． 【详解】由约束条件242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩，作出可行域如图，联立10220x x y -=⎧⎨+-=⎩，解得A （112，），1y x+的几何意义为可行域内的动点与定点P （0，-1）连线的斜率， 由图可知，113212PAk +==最大． 故答案为32． 【点睛】本题考查简单的线性规划，考查了数形结合的解题思想方法，属于中档题型．7．D解析：D 【解析】 【分析】设各项都是正数的等比数列{a n }的公比为q ，（q ＞0），由题意可得关于q 的式子，解之可得q ，而所求的式子等于q 2，计算可得． 【详解】设各项都是正数的等比数列{a n }的公比为q ，（q ＞0）由题意可得31212322a a a ⨯=+， 即q 2-2q-3=0， 解得q=-1（舍去），或q=3，故()26728967679a a qa a q a a a a ．++===++ 故选：D ． 【点睛】本题考查等差数列和等比数列的通项公式，求出公比是解决问题的关键，属基础题．8．A解析：A 【解析】 【分析】由余弦定理可知c 2＝a 2+b 2﹣2ab cos C ，进而求得a ﹣b 的表达式，根据表达式与0的大小，即可判断出a 与b 的大小关系． 【详解】解：∵∠C ＝120°，c =√2a ，∴由余弦定理可知c 2＝a 2+b 2﹣2ab cos C ，（√2a ）2＝a 2+b 2+ab ． ∴a 2﹣b 2＝ab ，a ﹣b =aba+b ， ∵a ＞0，b ＞0， ∴a ﹣b =aba+b ， ∴a ＞b 故选A ． 【点睛】本题考查余弦定理，特殊角的三角函数值，不等式的性质，比较法，属中档题．9．C解析：C 【解析】∵正项等比数列{}n a 的公比为3，且229m n a a a =∴2224222223339m n m n a a a a --+-⋅⋅⋅=⋅=∴6m n +=∴121121153()()(2)(2)62622624m n m n m n n m ⨯++=⨯+++≥⨯+=，当且仅当24m n ==时取等号. 故选C.点睛：利用基本不等式解题的注意点：（1）首先要判断是否具备了应用基本不等式的条件，即“一正、二正、三相等”，且这三个条件必须同时成立．（2）若不直接满足基本不等式的条件，需要通过配凑、进行恒等变形，构造成满足条件的形式，常用的方法有：“1”的代换作用，对不等式进行分拆、组合、添加系数等． （3）多次使用基本不等式求最值时，要注意只有同时满足等号成立的条件才能取得等号．10．C解析：C 【解析】由64S S -=6546a a a +=得，()22460,60q q a q q +-=+-=，解得2q，从而3522=28=16a a =⋅⨯，故选C.11．A解析：A 【解析】试题分析：331313log 1log log log 1n n n n a a a a +++=∴-=即13log 1n n a a +=13n naa +∴= ∴数列{}n a 是公比为3的等比数列335579246()393a a a q a a a ∴++=++=⨯=15793log ()5a a a ∴++=-．考点：1．等比数列的定义及基本量的计算；2．对数的运算性质．12．A解析：A 【解析】 【分析】画出可行域，平移基准直线20x y +=到可行域边界的点()1,1C -处，由此求得z 的最小值. 【详解】画出可行域如下图所示，平移基准直线20x y +=到可行域边界的点()1,1C -处，此时z 取得最小值为()2111⨯+-=. 故选：A.【点睛】本小题主要考查线性规划问题，考查数形结合的数学思想方法，属于基础题. 13．B解析：B【解析】【分析】【详解】∵点M(a,b)与点N(0,−1)在直线3x−4y+5=0的两侧,∴()()34530450a b -+⨯++<，即3450a b -+<，故①错误； 当0a >时,54a b +>，a +b 即无最小值，也无最大值，故②错误； 设原点到直线3x −4y +5=0的距离为d ,则1==d ,则22a b +>1，故③正确；当0a >且a ≠1时,11b a +-表示点M (a ,b )与P (1,−1)连线的斜率． ∵当0a =,b =54时,51194114b a ++==---,又直线3x −4y +5=0的斜率为34， 故11b a +-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，故④正确.∴正确命题的个数是2个. 故选B.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.14．D解析：D 【解析】 【分析】根据三角形内角和定理可知C =45°，再由正弦定理即可求出AB . 【详解】由内角和定理知C =180°−(60°+75°)=45°， 所以AB sinC=BCsinA， 即AB =BCsinC sinA=10×sin45°sin60°=10√63， 故选D.【点睛】本题主要考查了正弦定理，属于中档题.15．A解析：A 【解析】 【分析】画出满足条件的平面区域，求出角点的坐标，结合2yz x =-的几何意义求出其范围，即可得到答案. 【详解】由题意，画出满足条件的平面区域，如图所示： 由358y x x y =⎧⎨+=⎩，解得11A (，)，由1x y x=-⎧⎨=⎩，解得(11)B --，， 而2yz x =-的几何意义表示过平面区域内的点与0(2)C ，的直线斜率， 结合图象，可得1AC k =-，13BC k =， 所以2y z x =-的取值范围为113⎡⎤-⎢⎥⎣⎦，， 故选：A.【点睛】本题主要考查了简单的线性规划问题，其中解答中作出约束条件所表示的平面区域，结合图象确定出目标函数的最优解是解答的关键，着重考查了数形结合思想，以及计算能力，属于基础题.二、填空题16．【解析】由得：所以当且仅当时取等号故填解析：15【解析】由lg lg 2x y +=得：100xy =，所以11111111()100100505xy x y xy x y x y ⎛⎫+=+=+≥ ⎪⎝⎭，当且仅当10x y ==时，取等号，故填15. 17．【解析】试题分析：由题意可知解得所以考点：等差数列通项公式 解析：6766【解析】试题分析：由题意可知123417891463,3214a a a a a d a a a a d +++=+=++=+=，解得137,2266a d ==，所以5167466a a d =+=. 考点：等差数列通项公式． 18．【解析】【分析】根据题意化简得利用式相加得到进而得到即可求解结果【详解】因为所以所以将以上各式相加得又所以解得或【点睛】本题主要考查了数列的递推关系式应用其中解答中利用数列的递推关系式得到关于数列首解析：34，- 【解析】 【分析】根据题意，化简得22111n n n a a a ++-=-，利用式相加，得到2213113112S a a a --=-，进而得到211120a a --=，即可求解结果.【详解】因为22111n n n a a a ++-=-，所以22111n n n a a a ++-=-， 所以2222222213321313121,1,,1a a a a a a a a a -=--=--=-， 将以上各式相加，得2213113112S a a a --=-，又21313S a =，所以211120a a --=，解得13a =-或14a =.【点睛】本题主要考查了数列的递推关系式应用，其中解答中利用数列的递推关系式，得到关于数列首项的方程求解是解答的关键，着重考查了推理与运算能力，属于中档试题.19．【解析】【分析】由题意结合均值不等式首先求得的最小值然后结合恒成立的条件得到关于a 的不等式求解不等式即可确定实数a 的取值范围【详解】由可得故：当且仅当即时等号成立故只需又则即则的取值范围是【点睛】在 解析：[)1,+∞【解析】 【分析】由题意结合均值不等式首先求得141m n ++的最小值，然后结合恒成立的条件得到关于a 的不等式，求解不等式即可确定实数a 的取值范围. 【详解】由8m n +=可得19m n ++=，故：()1411411411419191n m m n m n m n m n +⎛⎫⎛⎫+=+++=+++ ⎪ ⎪+++⎝⎭⎝⎭11419⎛⨯++= ⎝≥，当且仅当12141n mn mm n+=⎧⎪+⎨=⎪+⎩，即3m=，5n=时等号成立，故只需11a≤，又0a>，则1a≥.即则a的取值范围是[)1,+∞.【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．20．7【解析】试题分析：作出不等式表示的平面区域得到及其内部其中把目标函数转化为表示的斜率为截距为由于当截距最大时最大由图知当过时截距最大最大因此由于当且仅当时取等号考点：1线性规划的应用；2利解析：7【解析】试题分析：作出不等式表示的平面区域，得到及其内部，其中把目标函数转化为，表示的斜率为，截距为，由于当截距最大时，最大，由图知，当过时，截距最大，最大，因此，，由于，当且仅当时取等号，.考点：1、线性规划的应用；2、利用基本不等式求最值.21．【解析】【分析】由题若对于任意的都有可得解出即可得出【详解】∵若对任意都有∴∴解得故答案为【点睛】本题考查了数列与函数的单调性不等式的解法考查了推理能力与计算能力属于中档题解析：17,212⎛⎫⎪⎝⎭【解析】 【分析】由题若对于任意的*n N ∈都有1n n a a +>，可得5610012a a a a -＜，＞，＜＜． 解出即可得出． 【详解】∵511,62,6n n a n n a a n -⎧⎛⎫-+<⎪ ⎪=⎝⎭⎨⎪≥⎩，若对任意*n N ∈都有1n n a a +>， ∴5610012a a a a -＜，＞，＜＜．． ∴11 0()510122a a a a --⨯+＜，＞，＜＜ ， 解得17 212a ＜＜． 故答案为17,212⎛⎫⎪⎝⎭．【点睛】本题考查了数列与函数的单调性、不等式的解法，考查了推理能力与计算能力，属于中档题．22．【解析】【分析】构造函数通过讨论其单调性即解析不等式的性质【详解】函数是定义在上的单调增函数若则即即故答案为：【点睛】此题考查利用函数单调性解析不等式的性质利用常见函数的单调性结合不等式的特征即可求解析：x c -【解析】 【分析】构造函数()f x x c =-，通过讨论其单调性即解析不等式的性质． 【详解】函数()f x x c =-，是定义在R 上的单调增函数， 若a c b c +>+，则()()f a c f b c +>+，即a c c b c c +->+-， 即a b >． 故答案为：x c - 【点睛】此题考查利用函数单调性解析不等式的性质，利用常见函数的单调性结合不等式的特征即可求解．23．【解析】【分析】利用1的代换将求式子的最小值等价于求的最小值再利用基本不等式即可求得最小值【详解】因为等号成立当且仅当故答案为：【点睛】本题考查1的代换和基本不等式求最值考查转化与化归思想的运用求解 解析：25【解析】 【分析】利用1的代换，将求式子43a b +的最小值等价于求43()(3)a b a b++的最小值，再利用基本不等式，即可求得最小值. 【详解】因为4343123()(3)491325b a a b a b a b a b +=++=+++≥+， 等号成立当且仅当21,55a b ==. 故答案为：25. 【点睛】本题考查1的代换和基本不等式求最值，考查转化与化归思想的运用，求解时注意一正、二定、三等的运用，特别是验证等号成立这一条件.24．【解析】【分析】表示出再表示出整理并观察等式列方程组即可求解【详解】等差数列的公差为前项和为设其首项为则=又数列也为公差为的等差数列首项为所以=即：整理得：上式对任意正整数n 成立则解得：【点睛】本题 解析：12【解析】【分析】表示出n S【详解】等差数列{}n a 的公差为()0d d ≠，前n 项和为n S ，设其首项为1a ， 则n S =()112n n na d -+，又数列也为公差为d=()1n d -()1n d =-=上式对任意正整数n成立，则)2120122d d d da d d⎧=⎪=⎪-+=⎪⎩，解得：12d =，134a =-【点睛】本题主要考查了等差数列的前n 项和及通项公式，考查了方程思想及转化思想、观察能力，属于中档题．25．【解析】【分析】由已知推导出=(=1+（）从而-=-由此能求出【详解】∵数列满足：∴（）+（）+……+（）=++……+==(∴=(；又+……+（）=1+++……+=1+=1+（）即=1+（）∴-=-解析：23-【解析】 【分析】 由已知推导出2n S =23(11)4n -，21n S -=1+13（1114n --），从而22n n a S =-21n S -=21132n --23，由此能求出2lim n n a →∞【详解】 ∵数列{}n a 满足：1 1a =，112nn n a a +⎛⎫+= ⎪⎝⎭， ∴（12a a +）+（34 a a +）+……+（212 n n a a -+）=12+312⎛⎫ ⎪⎝⎭+……+2112n -⎛⎫ ⎪⎝⎭=11124114n ⎛⎫- ⎪⎝⎭-=23(11)4n -， ∴2n S =23(11)4n -； 又12345 a a a a a +++++……+（2221 n n a a --+）=1+212⎛⎫ ⎪⎝⎭+412⎛⎫ ⎪⎝⎭+……+2212n -⎛⎫ ⎪⎝⎭=1+2111124114n -⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭-=1+13（1114n --）， 即21n S -=1+13（1114n --） ∴22n n a S =-21n S -=21132n --23 ∴2211lim lim(32n n n n a -→∞→∞=-2)3=-2 3， 故答案为：-2 3【点睛】本题考查数列的通项公式的求法，数列的极限的求法，考查逻辑思维能力及计算能力，属于中档题．三、解答题26．（1）2）不存在.【解析】【分析】（1）由已知11a b+=，利用基本不等式的和积转化可求2ab ≥，利用基本不等式可将33+a b 转化为ab ，由不等式的传递性，可求33+a b 的最小值；（2）由基本不等式可求23a b +的最小值为6>，故不存在．【详解】（111a b=+≥，得2ab ≥，且当a b ==故33+a b≥≥a b ==所以33+a b 的最小值为 （2）由（1）知，23a b +≥≥由于436>，从而不存在,a b ，使得236a b +=成立． 【考点定位】基本不等式．27．[]1,1-【解析】【分析】作出不等式组所表示的可行域，利用题中条件找出目标函数z ax y =+取得最大值和最小值的最优解，根据题意将直线z ax y =+与可行域边界线的斜率进行大小比较，可得出实数a 的取值范围.【详解】作出不等式组6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩所表示的可行域如下图所示：由z ax y =+得y ax z =-+，目标函数z ax y =+的最大值为39a +，最小值为33a -.∴当直线y ax z =-+经过点()3,9B 时，该直线在y 轴上的截距最大，当直线y ax z =-+经过点()3,3A -时，该直线在y 轴上的截距最小，结合图形可知，直线y ax z =-+的斜率不小于直线0x y +=的斜率，不大于直线60x y -+=的斜率，即11a -≤-≤，解得11a -≤≤，因此，实数a 的取值范围是[]1,1-.【点睛】本题考查线性目标函数最大值和最小值的最优解问题，对于这类问题，一般要利用数形结合思想，利用目标函数对应直线在坐标轴上的截距最值得出目标函数所在直线的斜率与可行域边界直线的斜率的大小关系来求解，考查数形结合思想，属于中等题.28．（1）3π；（2）2【解析】【分析】（1）可通过化简()sin2sin 0b A a A C -+=计算出cos A 的值，然后解出A 的值。

一、选择题1．(0分)[ID ：12717]设m ，n 为两条不同的直线，α，β为两个不同的平面，则（ ）A ．若//m α，//n α，则//m nB ．若//m α，//m β，则//αβC ．若//m n ，n α⊥，则m α⊥D ．若//m α，αβ⊥，则m β⊥2．(0分)[ID ：12716]已知集合{}220A x x x =-->，则A =RA ．{}12x x -<< B ．{}12x x -≤≤C ．}{}{|12x x x x <-⋃D ．}{}{|1|2x x x x ≤-⋃≥3．(0分)[ID ：12713]若cos(π4−α)=35，则sin2α=（ ） A ．725B ．15C ．−15D ．−7254．(0分)[ID ：12706]已知ABC 为等边三角形，2AB =，设P ，Q 满足AP AB λ=，()()1AQ AC λλ=-∈R ，若32BQ CP ⋅=-，则λ=（ ）A ．12B ．122± C ．1102± D ．3222± 5．(0分)[ID ：12686]我国古代数学名著《九章算术》对立体几何也有深入的研究，从其中的一些数学用语可见，譬如“堑堵”意指底面为直角三角形，且侧棱垂直于底面的三棱柱，“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥．现有一如图所示的“堑堵”即三棱柱111ABC A B C -，其中AC BC ⊥，若11AA AB ==，当“阳马”即四棱锥11B A ACC -体积最大时，“堑堵”即三棱柱111ABC A B C -的表面积为A 21B 31C ．232D ．3326．(0分)[ID ：12631]设函数f (x )=cos (x +3π)，则下列结论错误的是 A ．f(x)的一个周期为−2π B ．y=f(x)的图像关于直线x=83π对称 C ．f(x+π)的一个零点为x=6π D ．f(x)在(2π,π)单调递减7．(0分)[ID ：12668]已知1sin 34πα⎛⎫-= ⎪⎝⎭，则cos 23πα⎛⎫+= ⎪⎝⎭（ ）A ．58-B ．58 C ．78-D ．788．(0分)[ID ：12653]（2018年天津卷文）设变量x ，y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为 A ．6B ．19C ．21D ．459．(0分)[ID ：12649]若tan()24πα+=，则sin cos sin cos αααα-=+（ ）A ．12B ．2C ．2-D ．12-10．(0分)[ID ：12641]设n S 为等差数列{}n a 的前n 项和，若3243S S S =+，12a =，则5a =A ．12-B ．10-C ．10D ．1211．(0分)[ID ：12636]如图，在△ABC 中, 13AN NC =,P 是BN 上的一点,若29AP m AB AC −−→−−→−−→=+,则实数m 的值为( )A ．B ．C ．19D ．12．(0分)[ID ：12700]如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数()f x ，则()y f x =在[0,]π上的图象大致为（ ）A ．B ．C ．D ．13．(0分)[ID ：12699]《莱茵德纸草书》是世界上最古老的数学著作之一．书中有这样一道题目：把100个面包分给5个人，使每个人所得成等差数列，且使较大的三份之和的17是较小的两份之和，则最小的一份为（ ）A ．53B ．103 C ．56 D ．11614．(0分)[ID ：12657]函数()(1)lg(1)35f x x x x =-+--的零点个数为（ ）A ．3B ．2C ．1D ．015．(0分)[ID ：12652]将直线2x －y ＋λ＝0沿x 轴向左平移1个单位，所得直线与圆x 2＋y 2＋2x －4y ＝0相切，则实数λ的值为( ) A ．－3或7 B ．－2或8 C ．0或10D ．1或11二、填空题16．(0分)[ID ：12824]在区间[﹣2，4]上随机地取一个数x ，若x 满足|x|≤m 的概率为，则m= _________ ．17．(0分)[ID ：12818]在ABC ∆中，若3B π=，3AC =2AB BC +的最大值为__________．18．(0分)[ID ：12817]已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 是球O 的直径.若平面SCA ⊥平面SCB ，SA AC =，SB BC =，三棱锥S ABC -的体积为9，则球O 的表面积为______． 19．(0分)[ID ：12813]函数2sin 26y x π⎛⎫=-⎪⎝⎭（[]0,x π∈）为增函数的区间是 ． 20．(0分)[ID ：12780]如图，在等腰三角形ABC 中，已知1AB AC ==，120A ∠=︒，E F 、分别是边AB AC 、上的点，且,AE AB AF AC λμ==,其中(),0,1λμ∈且41λμ+=，若线段EF BC 、的中点分别为M N 、，则MN 的最小值是_____.21．(0分)[ID ：12761]在四面体ABCD 中，=2,60,90AB AD BAD BCD =∠=︒∠=︒，二面角A BD C --的大小为150︒，则四面体ABCD 外接球的半径为__________． 22．(0分)[ID ：12740]从1，2，3，4这四个数中一次随机取两个数，则其中一个数是另一个的两倍的概率是______23．(0分)[ID ：12729]若()1,x ∈+∞，则131y x x =+-的最小值是_____． 24．(0分)[ID ：12810]若三点1(2,3),(3,2),(,)2A B C m --共线，则m 的值为 ．25．(0分)[ID ：12749]若两个向量a 与b 的夹角为θ，则称向量“a b ⨯”为向量的“外积”，其长度为sin a b a b θ⨯=.若已知1a =，5b =，4a b ⋅=-，则a b ⨯= . 三、解答题26．(0分)[ID ：12912]如图，四棱锥P ABC -中，PA ⊥平面ABCD ，AD BC ∥，3AB AD AC ===，4PA BC ，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN ∥平面PAB ； （II ）求四面体N BCM -的体积.27．(0分)[ID ：12860]如图，在三棱柱111ABC A B C -中，侧棱垂直于底面，1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ； （2）求证:1C F ∥平面ABE ； （3）求三棱锥E ABC -体积．28．(0分)[ID ：12851]等比数列{}n a 的各项均为正数，且212326231,9a a a a a +==.（1）求数列{}n a 的通项公式； （2）设 31323log log ......log nn b a a a =+++，求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T . 29．(0分)[ID ：12850]已知四点A （-3，1），B （-1，-2），C （2，0），D （23,4m m +） （1）求证：AB BC ⊥； (2) //AD BC ，求实数m 的值.30．(0分)[ID ：12837]已知ABC ∆的三个顶点坐标分别为()4,2A --，()4,2B ，()13C ，．（1）求边AB 上的高所在直线的一般式方程； （2）求边AB 上的中线所在直线的一般式方程.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．C2．B3．D4．A5．C6．D7．C8．C9．D10．B11．C12．B13．A14．B15．A二、填空题16．3【解析】【分析】【详解】如图区间长度是6区间﹣24上随机地取一个数x若x满足|x|≤m的概率为若m对于3概率大于若m小于3概率小于所以m=3故答案为317．【解析】【分析】【详解】设最大值为考点：解三角形与三角函数化简点评：借助于正弦定理三角形内角和将边长用一内角表示转化为三角函数求最值只需将三角函数化简为的形式18．36π【解析】三棱锥S−ABC的所有顶点都在球O的球面上SC是球O的直径若平面SCA⊥平面SCBSA=ACSB=BC三棱锥S−ABC的体积为9可知三角形SBC与三角形SAC 都是等腰直角三角形设球的半19．【解析】试题分析：因为所以只要求函数的减区间即可解可得即所以故答案为考点：三角函数的图象和基本性质的运用【易错点晴】本题以函数的表达式的单调区间为背景考查的是三角函数中形如的正弦函数的图象和性质解答20．【解析】【分析】根据条件及向量数量积运算求得连接由三角形中线的性质表示出根据向量的线性运算及数量积公式表示出结合二次函数性质即可求得最小值【详解】根据题意连接如下图所示:在等腰三角形中已知则由向量数21．【解析】画出图象如下图所示其中为等边三角形边的中点为等边三角形的中心(等边三角形四心合一);球心在点的正上方也在点的正上方依题意知在中所以外接圆半径22．【解析】【分析】【详解】解：从1234这四个数中一次随机取两个数有（12）（13）（14）（23）（24）（34）共6种情况；其中其中一个数是另一个的两倍的有两种即（12）（24）；则其概率为；故答23．【解析】【分析】由已知可知然后利用基本不等式即可求解【详解】解：（当且仅当取等号）故答案为【点睛】本题主要考查了利用基本不等式求最值解题的关键是配凑积为定值属于基础试题24．【解析】试题分析：依题意有即解得考点：三点共线25．3【解析】【分析】【详解】故答案为3【点评】本题主要考查以向量的数量积为载体考查新定义利用向量的数量积转化是解决本题的关键三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．C 解析：C 【解析】 【分析】根据空间线面关系、面面关系及其平行、垂直的性质定理进行判断． 【详解】对于A 选项，若//m α，//n α，则m 与n 平行、相交、异面都可以，位置关系不确定；对于B 选项，若l αβ=，且//m l ，m α⊄，m β⊄，根据直线与平面平行的判定定理知，//m α，//m β，但α与β不平行；对于C 选项，若//m n ，n α⊥，在平面α内可找到两条相交直线a 、b 使得n a ⊥，n b ⊥，于是可得出m a ⊥，m b ⊥，根据直线与平面垂直的判定定理可得m α⊥； 对于D 选项，若αβ⊥，在平面α内可找到一条直线a 与两平面的交线垂直，根据平面与平面垂直的性质定理得知a β⊥，只有当//m a 时，m 才与平面β垂直． 故选C ． 【点睛】本题考查空间线面关系以及面面关系有关命题的判断，判断时要根据空间线面、面面平行与垂直的判定与性质定理来进行，考查逻辑推理能力，属于中等题．2．B解析：B 【解析】分析：首先利用一元二次不等式的解法，求出220x x -->的解集，从而求得集合A ，之后根据集合补集中元素的特征，求得结果. 详解：解不等式220x x -->得12x x -或， 所以{}|12A x x x =<->或，所以可以求得{}|12R C A x x =-≤≤，故选B.点睛：该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题，在解题的过程中，需要明确一元二次不等式的解集的形式以及补集中元素的特征，从而求得结果.3．D解析：D 【解析】试题分析：cos[2(π4−α)]=2cos 2(π4−α)−1=2×(35)2−1=−725，且cos[2(π4−α)]=cos[π2−2α]=sin2α，故选D. 【考点】三角恒等变换【名师点睛】对于三角函数的给值求值问题，关键是把待求角用已知角表示： （1）已知角为两个时，待求角一般表示为已知角的和或差．（2）已知角为一个时，待求角一般与已知角成“倍的关系”或“互余、互补”关系．4．A解析：A 【解析】 【分析】运用向量的加法和减法运算表示向量BQ BA AQ =+，CP CA AP =+，再根据向量的数量积运算，建立关于λ的方程，可得选项. 【详解】∵BQ BA AQ =+，CP CA AP =+，∴()()BQ CP BA AQ CA AP AB AC AB AP AC AQ AQ AP ⋅=+⋅+=⋅-⋅-⋅+⋅()()2211AB AC AB AC AB AC λλλλ=⋅---+-⋅()()232441212222λλλλλλ=---+-=-+-=-，∴12λ=.故选：A. 5．C解析：C 【解析】分析：由四棱锥11B A ACC -的体积是三棱柱体积的23，知只要三棱柱体积最大，则四棱锥体积也最大，求出三棱柱的体积后用基本不等式求得最大值，及取得最大值时的条件，再求表面积．详解：四棱锥11B A ACC -的体积是三棱柱体积的23，11111122ABC A B C V AC BC AA AC BC -=⋅⋅=⋅222111()444AC BC AB ≤+==，当且仅当2AC BC ==时，取等号．∴12(1)122222S =⨯⨯+++⨯32+=． 故选C ．点睛：本题考查棱柱与棱锥的体积，考查用基本不等式求最值．解题关键是表示出三棱柱的体积．6．D解析：D 【解析】f (x )的最小正周期为2π，易知A 正确； f 8π3⎛⎫⎪⎝⎭＝cos 8ππ33⎛⎫+ ⎪⎝⎭＝cos3π＝－1，为f (x )的最小值，故B 正确；∵f (x ＋π)＝cos ππ3x ⎛⎫++ ⎪⎝⎭＝－cos π3x ⎛⎫+ ⎪⎝⎭，∴f ππ6⎛⎫+ ⎪⎝⎭＝－cos ππ63⎛⎫+ ⎪⎝⎭＝－cos 2π＝0，故C 正确； 由于f 2π3⎛⎫⎪⎝⎭＝cos 2ππ33⎛⎫+ ⎪⎝⎭＝cosπ＝－1，为f (x )的最小值，故f (x )在,2ππ⎛⎫ ⎪⎝⎭上不单调，故D 错误． 故选D.7．C解析：C 【解析】 由题意可得：1sin sin cos 32664ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 则217cos 2cos 22cos 121366168πππααα⎛⎫⎛⎫⎛⎫+=+=+-=⨯-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.本题选择C 选项.8．C解析：C 【解析】分析：首先画出可行域，然后结合目标目标函数的几何意义确定函数取得最大值的点，最后求解最大值即可.详解：绘制不等式组表示的平面区域如图所示，结合目标函数的几何意义可知目标函数在点A 处取得最大值，联立直线方程：51x y x y +=⎧⎨-+=⎩，可得点A 的坐标为：()2,3A ，据此可知目标函数的最大值为：max 35325321z x y =+=⨯+⨯=.本题选择C 选项.点睛：求线性目标函数z ＝ax ＋by (ab ≠0)的最值，当b ＞0时，直线过可行域且在y 轴上截距最大时，z 值最大，在y 轴截距最小时，z 值最小；当b ＜0时，直线过可行域且在y 轴上截距最大时，z 值最小，在y 轴上截距最小时，z 值最大.9．D解析：D 【解析】 由tan()24πα+=有tan 112,tan 1tan 3ααα+==-，所以11sin cos tan 1131sin cos tan 1213αααααα---===-+++，选D.点睛：本题主要考查两角和的正切公式以及同角三角函数的基本关系式，属于中档题。

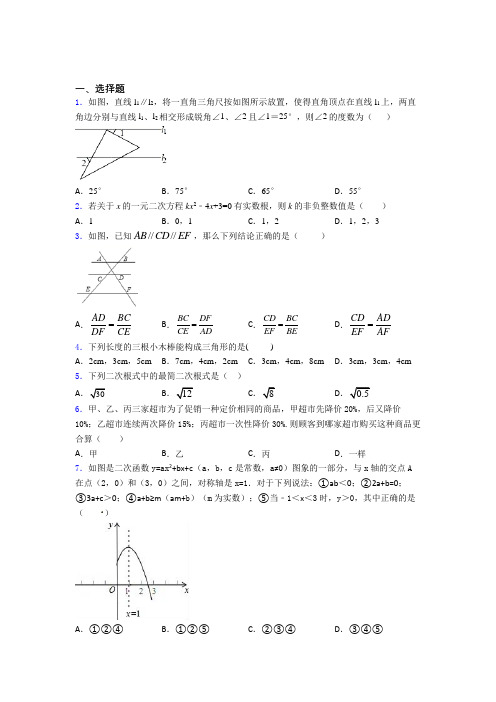
一、选择题1．如图，直线l1∥l2，将一直角三角尺按如图所示放置，使得直角顶点在直线l1上，两直角边分别与直线l1、l2相交形成锐角∠1、∠2且∠1＝25°，则∠2的度数为（）A．25°B．75°C．65°D．55°2．若关于x的一元二次方程kx2﹣4x+3=0有实数根，则k的非负整数值是（）A．1B．0，1C．1，2D．1，2，33．如图，已知////AB CD EF，那么下列结论正确的是（）A．AD BCDF CE=B．BC DFCE AD=C．CD BCEF BE=D．CD ADEF AF=4．下列长度的三根小木棒能构成三角形的是()A．2cm，3cm，5cm B．7cm，4cm，2cm C．3cm，4cm，8cm D．3cm，3cm，4cm 5．下列二次根式中的最简二次根式是（）A．30B．12C．8D．0.56．甲、乙、丙三家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%；乙超市连续两次降价15%；丙超市一次性降价30%.则顾客到哪家超市购买这种商品更合算（）A．甲B．乙C．丙D．一样7．如图是二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A 在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）A．①②④B．①②⑤C．②③④D．③④⑤8．如图，是由四个相同的小正方体组成的立体图形，它的左视图是（ ）A ．B ．C ．D ．9．如图，矩形纸片ABCD 中，4AB =，6BC =，将ABC 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（ ）A ．35B ．53C ．73D ．5410．如图,在△ABC 中,∠ACB=90°, ∠ABC=60°, BD 平分∠ABC ,P 点是BD 的中点,若AD=6, 则CP 的长为( )A ．3.5B ．3C ．4D ．4.511．甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x 个零件，下列方程正确的是（ ） A ．1201508x x =- B ．1201508x x=+ C ．1201508x x=- D ．1201508x x =+ 12．如图，AB ，AC 分别是⊙O 的直径和弦，OD AC ⊥于点D ，连接BD ，BC ，且10AB =，8AC =，则BD 的长为（ ）A ．5B ．4C ．213D ．4.813．如图所示，已知A （12，y 1），B(2,y 2)为反比例函数1y x =图像上的两点，动点P(x ，0)在x 正半轴上运动，当线段AP 与线段BP 之差达到最大时，点P 的坐标是（ ）A ．(12，0) B ．(1,0) C ．(32,0) D ．(52,0) 14．有31位学生参加学校举行的“最强大脑”智力游戏比赛，比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差，如果去掉一个最高分和一个最低分，则一定不发生变化的是（ ） A ．中位数 B ．平均数 C ．众数 D ．方差 15．点 P （m + 3，m + 1）在x 轴上，则P 点坐标为（ ）A ．（0，﹣2）B ．（0，﹣4）C ．（4，0）D ．（2，0）16．如图，AB 是一垂直于水平面的建筑物，某同学从建筑物底端B 出发，先沿水平方向向右行走20米到达点C ，再经过一段坡度（或坡比）为i=1：0.75、坡长为10米的斜坡CD 到达点D ，然后再沿水平方向向右行走40米到达点E （A ，B ，C ，D ，E 均在同一平面内）．在E 处测得建筑物顶端A 的仰角为24°，则建筑物AB 的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°=0.45）（ ）A ．21.7米B ．22.4米C ．27.4米D ．28.8米17．下表是某学习小组一次数学测验的成绩统计表： 分数/分 70 80 90100 人数/人13x1已知该小组本次数学测验的平均分是85分，则测验成绩的众数是（ ） A ．80分B ．85分C ．90分D ．80分和90分18．阅读理解：已知两点1122,,()(),M x y N x y ，则线段MN 的中点(),K x y 的坐标公式为：122x x x +=，122y y y +=．如图，已知点O 为坐标原点，点()30A -,，O 经过点A ，点B 为弦PA 的中点．若点(),P a b ，则有,a b 满足等式：229a b +=．设(),B m n ，则,m n 满足的等式是（ ）A ．229m n +=B ．223922m n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭C ．()()222323m n ++=D ．()222349m n ++=19．如图，A ，B ，P 是半径为2的⊙O 上的三点，∠APB ＝45°，则弦AB 的长为（ ）A ．2B ．4C ．22D ．220．已知平面内不同的两点A （a +2，4）和B （3，2a +2）到x 轴的距离相等，则a 的值为( ) A ．﹣3 B ．﹣5C ．1或﹣3D ．1或﹣521．如图，菱形ABCD 的一边中点M 到对角线交点O 的距离为5cm ，则菱形ABCD 的周长为（ ）A ．5cmB ．10cmC ．20cmD ．40cm22．将抛物线23y x =向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A ．23(2)3y x =++B ．23(2)3y x =-+C ．23(2)3y x =+-D ．23(2)3y x =-- 23．如图是某个几何体的三视图，该几何体是（）A ．三棱柱B ．三棱锥C ．圆柱D ．圆锥 24．若一组数据2，3，，5，7的众数为7，则这组数据的中位数为( )A ．2B ．3C ．5D ．725．若一元二次方程x 2﹣2kx +k 2＝0的一根为x ＝﹣1，则k 的值为（ ） A ．﹣1B ．0C ．1或﹣1D ．2或026．不等式x+1≥2的解集在数轴上表示正确的是（ ） A ． B ． C ．D ．27．如图，点A ，B 在反比例函数y ＝1x（x ＞0）的图象上，点C ，D 在反比例函数y ＝k x（k ＞0）的图象上，AC ∥BD ∥y 轴，已知点A ，B 的横坐标分别为1；2，△OAC 与△CBD 的面积之和为94，则k 的值为（ ）A ．2B ．3C ．4D ．28．如图，点P 是矩形ABCD 的对角线AC 上一点，过点P 作EF ∥BC ，分别交AB ，CD 于E 、F ，连接PB 、PD ．若AE=2，PF=8．则图中阴影部分的面积为（ ）A ．10B ．12C ．16D ．1829．如图，在平行四边形ABCD 中，M 、N 是BD 上两点，BM DN =，连接AM 、MC 、CN 、NA ，添加一个条件，使四边形AMCN 是矩形，这个条件是( )A ．12OM AC =B ．MB MO =C ．BD AC ⊥ D ．AMB CND ∠=∠30．下列各式化简后的结果为2 的是（ ） A 6B 12C 18D 36【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．C2．A3．A4．D5．A6．C7．A8．A9．B10．B11．D12．C13．D14．A15．D16．A17．D18．D19．C20．A21．D22．A23．A24．C25．A26．A27．C28．C29．A30．C2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．C解析：C【解析】【分析】依据∠1＝25°，∠BAC＝90°，即可得到∠3＝65°，再根据平行线的性质，即可得到∠2＝∠3＝65°．【详解】如图，∵∠1＝25°，∠BAC＝90°，∴∠3＝180°-90°-25°=65°，∵l1∥l2，∴∠2＝∠3＝65°，故选C．【点睛】本题考查的是平行线的性质，运用两直线平行，同位角相等是解答此题的关键．2．A解析：A【解析】【分析】【详解】由题意得，根的判别式为△=(-4)2-4×3k，由方程有实数根，得(-4)2-4×3k≥0，解得k≤43，由于一元二次方程的二次项系数不为零，所以k≠0，所以k的取值范围为k≤43且k≠0，即k的非负整数值为1，故选A．3．A解析：A【解析】【分析】已知AB∥CD∥EF，根据平行线分线段成比例定理，对各项进行分析即可．【详解】∵AB∥CD∥EF，∴AD BC DF CE．故选A．【点睛】本题考查平行线分线段成比例定理，找准对应关系，避免错选其他答案．4．D解析：D【解析】【详解】A．因为2+3=5，所以不能构成三角形，故A错误；B．因为2+4＜6，所以不能构成三角形，故B错误；C．因为3+4＜8，所以不能构成三角形，故C错误；D．因为3+3＞4，所以能构成三角形，故D正确．故选D．5．A解析：A【解析】【分析】根据最简二次根式的概念判断即可．【详解】ABC，不是最简二次根式；D故选：A．【点睛】此题考查最简二次根式的概念，解题关键在于掌握（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．6．C解析：C【解析】试题分析：设商品原价为x，表示出三家超市降价后的价格，然后比较即可得出答案．解：设商品原价为x，甲超市的售价为：x（1﹣20%）（1﹣10%）=0.72x；乙超市售价为：x（1﹣15%）2=0.7225x；丙超市售价为：x（1﹣30%）=70%x=0.7x；故到丙超市合算．故选C．考点：列代数式．7．A解析：A【解析】【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴判定b与0的关系以及2a+b=0；当x=﹣1时，y=a﹣b+c；然后由图象确定当x 取何值时，y＞0．【详解】①∵对称轴在y 轴右侧， ∴a 、b 异号， ∴ab ＜0，故正确；②∵对称轴1,2bx a=-= ∴2a+b=0；故正确； ③∵2a+b=0， ∴b=﹣2a ，∵当x=﹣1时，y=a ﹣b+c ＜0， ∴a ﹣（﹣2a ）+c=3a+c ＜0，故错误； ④根据图示知，当m=1时，有最大值； 当m≠1时，有am 2+bm+c≤a+b+c ， 所以a+b≥m （am+b ）（m 为实数）． 故正确．⑤如图，当﹣1＜x ＜3时，y 不只是大于0． 故错误． 故选A ． 【点睛】本题主要考查了二次函数图象与系数的关系，关键是熟练掌握①二次项系数a 决定 抛物线的开口方向，当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；②一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左； 当a 与b 异号时（即ab ＜0），对称轴在y 轴右．（简称：左同右异）③常数项c 决定抛物线与y 轴交点，抛物线与y 轴交于（0，c ）．8．A解析：A 【解析】 【分析】 【详解】从左面看，这个立体图形有两层，且底层有两个小正方形，第二层的左边有一个小正方形． 故选A ．9．B解析：B 【解析】 【分析】由折叠的性质得到AE=AB ，∠E=∠B=90°，易证Rt △AEF ≌Rt △CDF ，即可得到结论EF=DF ；易得FC=FA ，设FA=x ，则FC=x ，FD=6-x ，在Rt △CDF 中利用勾股定理得到关于x 的方程x 2=42+（6-x ）2，解方程求出x 即可．【详解】∵矩形ABCD 沿对角线AC 对折，使△ABC 落在△ACE 的位置，∴AE=AB ，∠E=∠B=90°，又∵四边形ABCD 为矩形，∴AB=CD ，∴AE=DC ，而∠AFE=∠DFC ，∵在△AEF 与△CDF 中，AFE CFD E DAE CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△AEF ≌△CDF （AAS ），∴EF=DF ；∵四边形ABCD 为矩形，∴AD=BC=6，CD=AB=4，∵Rt △AEF ≌Rt △CDF ，∴FC=FA ，设FA=x ，则FC=x ，FD=6-x ，在Rt △CDF 中，CF 2=CD 2+DF 2，即x 2=42+（6-x ）2，解得x ＝133， 则FD ＝6-x=53. 故选B ．【点睛】考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应边相等．也考查了矩形的性质和三角形全等的判定与性质以及勾股定理． 10．B解析：B【解析】【分析】【详解】解：∵∠ACB ＝90°，∠ABC ＝60°，∴∠A ＝30°，∵BD 平分∠ABC ，∴∠ABD ＝12∠ABC ＝30°， ∴∠A ＝∠ABD ，∴BD ＝AD ＝6，∵在Rt △BCD 中，P 点是BD 的中点，∴CP ＝12BD ＝3． 故选B ． 11．D解析：D【解析】【分析】首先用x 表示甲和乙每小时做的零件个数，再根据甲做120个所用的时间与乙做150个所用的时间相等即可列出一元一次方程.【详解】解：∵甲每小时做x 个零件，∴乙每小时做（x+8）个零件，∵甲做120个所用的时间与乙做150个所用的时间相等，∴1201508x x =+， 故选D.【点睛】本题考查了分式方程的实际应用，熟练掌握是解题的关键. 12．C解析：C【解析】【分析】先根据圆周角定理得∠ACB=90°，则利用勾股定理计算出BC=6，再根据垂径定理得到142CD AD AC ===，然后利用勾股定理计算BD 的长． 【详解】 ∵AB 为直径，∴90ACB ︒∠=，∴6BC ==，∵OD AC ⊥， ∴142CD AD AC ===，在Rt CBD ∆中，BD ==故选C ．【点睛】 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．解析：D【解析】【分析】求出AB 的坐标，设直线AB 的解析式是y=kx+b ，把A 、B 的坐标代入求出直线AB 的解析式，根据三角形的三边关系定理得出在△ABP 中，|AP-BP|＜AB ，延长AB 交x 轴于P′，当P 在P′点时，PA-PB=AB ，此时线段AP 与线段BP 之差达到最大，求出直线AB 于x 轴的交点坐标即可．【详解】∵把A （12，y 1），B （2，y 2）代入反比例函数y=1x 得：y 1=2，y 2=12， ∴A （12，2），B （2，12）， ∵在△ABP 中，由三角形的三边关系定理得：|AP-BP|＜AB ，∴延长AB 交x 轴于P′，当P 在P′点时，PA-PB=AB ，即此时线段AP 与线段BP 之差达到最大，设直线AB 的解析式是y=kx+b ，把A 、B 的坐标代入得：122122k b k b ⎧+⎪⎪⎨⎪+⎪⎩＝＝， 解得：k=-1，b=52， ∴直线AB 的解析式是y=-x+52， 当y=0时，x=52， 即P （52，0）， 故选D ．【点睛】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用，解此题的关键是确定P 点的位置，题目比较好，但有一定的难度．解析：A【解析】【分析】根据中位数的定义：位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数．【详解】去掉一个最高分和一个最低分对中位数没有影响，故选A．【点睛】考查了统计量的选择，解题的关键是了解中位数的定义.15．D解析：D【解析】【分析】根据点在x轴上的特征,纵坐标为0,可得m+1=0,解得:m=-1,然后再代入m+3,可求出横坐标.【详解】解:因为点P（m + 3，m + 1）在x轴上,所以m+1=0,解得:m=-1,所以m+3=2,所以P点坐标为（2，0）.故选D.【点睛】本题主要考查点在坐标轴上的特征,解决本题的关键是要熟练掌握点在坐标轴上的特征. 16．A解析：A【解析】【分析】作BM⊥ED交ED的延长线于M，CN⊥DM于N．首先解直角三角形Rt△CDN，求出CN，DN，再根据tan24°=AMEM，构建方程即可解决问题.【详解】作BM⊥ED交ED的延长线于M，CN⊥DM于N．在Rt△CDN中，∵140.753CNDN==，设CN=4k，DN=3k，∴CD=10，∴（3k ）2+（4k ）2=100，∴k=2，∴CN=8，DN=6，∵四边形BMNC 是矩形，∴BM=CN=8，BC=MN=20，EM=MN+DN+DE=66，在Rt △AEM 中，tan24°=AM EM ， ∴0.45=866AB +， ∴AB=21.7（米），故选A ．【点睛】本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键．17．D解析：D【解析】【分析】先通过加权平均数求出x 的值，再根据众数的定义就可以求解．【详解】解：根据题意得：70+80×3+90x+100=85（1+3+x+1）， x=3∴该组数据的众数是80分或90分．故选D ．【点睛】本题考查了加权平均数的计算和列方程解决问题的能力，解题的关键是利用加权平均数列出方程．通过列方程求出x 是解答问题的关键．18．D解析：D【解析】【分析】根据中点坐标公式求得点B 的坐标，然后代入,a b 满足的等式进行求解即可.【详解】∵点()30A -,，点(),P a b ，点(),B m n 为弦PA 的中点， ∴32a m -+=，02b n +=， ∴23,2a m b n =+=，又,a b 满足等式：229a b +=，∴()222349m n ++=，故选D ．【点睛】本题考查了坐标与图形性质，解题的关键是理解中点坐标公式． 19．C解析：C【解析】【分析】由A 、B 、P 是半径为2的⊙O 上的三点，∠APB=45°，可得△OAB 是等腰直角三角形，继而求得答案．【详解】解：连接OA ，OB ．∵∠APB =45°，∴∠AOB =2∠APB =90°．∵OA =OB =2，∴AB =22OA OB +=22．故选C ．20．A解析：A【解析】分析：根据点A （a ＋2，4）和B （3，2a ＋2）到x 轴的距离相等，得到4＝|2a ＋2|，即可解答．详解：∵点A （a ＋2，4）和B （3，2a ＋2）到x 轴的距离相等，∴4＝|2a ＋2|，a ＋2≠3，解得：a ＝−3，故选A ．点睛：考查点的坐标的相关知识；用到的知识点为：到x 轴和y 轴的距离相等的点的横纵坐标相等或互为相反数．21．D解析：D【解析】【分析】根据菱形的性质得出AB=BC=CD=AD ，AO=OC ，根据三角形的中位线求出BC ，即可得出答案．【详解】∵四边形ABCD 是菱形，∴AB=BC=CD=AD ，AO=OC ，∵AM=BM ，∴BC=2MO=2×5cm=10cm ， 即AB=BC=CD=AD=10cm ，即菱形ABCD 的周长为40cm ，故选D ．【点睛】本题考查了菱形的性质和三角形的中位线定理，能根据菱形的性质得出AO=OC 是解此题的关键．22．A解析：A【解析】【分析】直接根据“上加下减，左加右减”的原则进行解答即可．【详解】将抛物线23y x =向上平移3个单位，再向左平移2个单位，根据抛物线的平移规律可得新抛物线的解析式为23(2)3y x =++，故答案选A ． 23．A解析：A【解析】试题分析：观察可得，主视图是三角形，俯视图是两个矩形，左视图是矩形，所以这个几何体是三棱柱，故选A ．考点：由三视图判定几何体.24．C解析：C【解析】试题解析：∵这组数据的众数为7，∴x=7，则这组数据按照从小到大的顺序排列为：2，3，5，7，7，中位数为：5．故选C ．考点：众数；中位数.25．A解析：A【分析】把x ＝﹣1代入方程计算即可求出k 的值．【详解】解：把x ＝﹣1代入方程得：1+2k +k 2＝0，解得：k ＝﹣1，故选：A ．【点睛】此题考查了一元二次方程的解，方程的解即为能使方程左右两边相等的未知数的值．26．A解析：A【解析】试题解析：∵x+1≥2，∴x ≥1．故选A ．考点：解一元一次不等式；在数轴上表示不等式的解集．27．C解析：C【解析】【分析】由题意，可得A （1，1），C （1，k ），B （2，12），D （2，12k ），则△OAC 面积＝12(k-1)，△CBD 的面积＝12×(2-1)×(12k-12)=14(k-1)，根据△OAC 与△CBD 的面积之和为94，即可得出k 的值．【详解】∵AC ∥BD ∥y 轴，点A ，B 的横坐标分别为1、2，∴A （1，1），C （1，k ），B （2，12），D （2，12k ）， ∴△OAC 面积＝12×1×(k-1)，△CBD 的面积＝12×(2-1)×(12k-12)=14(k-1)， ∵△OAC 与△CBD 的面积之和为94， ∴12(k-1)+ 14(k-1)=94， ∴k ＝4．故选C ．【点睛】本题考查反比例函数系数k 的几何意义，三角形面积的计算，解题的关键是用k 表示出△OAC 与△CBD 的面积．28．C解析：C【解析】首先根据矩形的特点，可以得到S △ADC =S △ABC ，S △AMP =S △AEP ，S △PFC =S △PCN ，最终得到S 矩形EBNP = S 矩形MPFD ,即可得S △PEB =S △PFD ，从而得到阴影的面积．【详解】作PM ⊥AD 于M ，交BC 于N ．则有四边形AEPM ，四边形DFPM ，四边形CFPN ，四边形BEPN 都是矩形， ∴S △ADC =S △ABC ，S △AMP =S △AEP ，S △PFC =S △PCN∴S 矩形EBNP = S 矩形MPFD ,又∵S △PBE = 12S 矩形EBNP ，S △PFD =12S 矩形MPFD ， ∴S △DFP =S △PBE =12×2×8=8， ∴S 阴=8+8=16，故选C ．【点睛】 本题考查矩形的性质、三角形的面积等知识，解题的关键是证明S △PEB =S △PFD ．29．A解析：A【解析】【分析】由平行四边形的性质可知：OA OC =，OB OD =，再证明OM ON =即可证明四边形AMCN 是平行四边形．【详解】∵四边形ABCD 是平行四边形，∴OA OC =，OB OD =，∵对角线BD 上的两点M 、N 满足BM DN =，∴OB BM OD DN -=-，即OM ON =，∴四边形AMCN 是平行四边形， ∵12OM AC =， ∴MN AC =，∴四边形AMCN 是矩形．故选：A ．【点睛】本题考查了矩形的判定，平行四边形的判定与性质，解题的关键是灵活运用所学知识解决问题．30．C解析：C【解析】A不能化简；B C，故正确；D，故错误；故选C．点睛：本题主要考查二次根式，熟练掌握二次根式的性质是解题的关键．。

深圳西丽湖世纪星学校小升初数学期末试卷培优测试卷一、选择题1．用同样大小的正方体木块拼成一个大正方形，下面小正方体的块数不能拼成大正方体的是（ ）． A ．24块B ．27块C ．64块2．一壶油，用去 15 ，还剩5千克．这壶油原来有多少千克？正确的算式是( )．A ．5＋5× 15B ．5÷ 15C ．5÷(1＋ 15)D ．5÷(1－ 15)3．一个三角形三个内角度数的比是2:3:5，这个三角形中最大的内角是（ ）。

A ．锐角B ．直角C ．钝角4．学校电脑班有女生18人，比男生人数的13少2人，电脑班有多少男生？设男生有x人，下列方程正确的是（ ）。

A ．18－13x ＝2B ．13x －2＝18C ．13x ＋2＝18D ．（x ＋2）×13＝185．一个立方体的六个面上分别标上了数1点、2点、3点、4点、5点、6点，下图是从三个不同角度观察到的情况．“3点”这一面相对的面是（ ）A ．2点B ．4点C ．6点或4点6．下列说法错误的是（ ）。

A ．如果1=a b ÷，那么a 一定是b 的倒数B ．1千米增加15后，又减少15千米，结果还是1千米C ．正方体的棱长扩大为原来的3倍，那么表面积扩大为原来的6倍，体积扩大为原来的9倍7．a 是奇数，b 是偶数。

下面式子的结果是奇数的是（ ）。

A ．3a b +B ．2a b +C ．()2a b +D ．3ab8．某通讯公司的手机收费按原标准每分钟降低了a 元，再次下调了25%，现在的收费标准为每分钟b 元，原收费标准是（ ）。

A ．43b a -B ．43baC ．43b a +D ．34b a +9．如左图，照样子摆三角形，摆12个三角形一共需要（ ）根小棒。

A ．24B ．25C ．36二、填空题10．15公顷＝________平方米4.07吨＝________吨________千克2小时15分＝________小时0.45升＝________毫升 11．()()()()125%12:8÷====（填小数）。

一、选择题1．若12a = ，3b =，且0a b <，则+a b 的值为（ ） A ．52 B ．52- C ．25± D ．52± 2．13-的倒数的绝对值（ ）A ．－3B ．13-C ．3D ．13 3．如果a ＝14-，b ＝－2，c ＝324-，那么︱a ︱+︱b ︱-︱c ︱等于（ ） A ．-12 B ．112 C ．12 D ．-112 4．下列计算正确的是（ ）A ．|﹣3|＝﹣3B ．﹣2﹣2＝0C ．﹣14＝1D ．0.1252×（﹣8）2＝1 5．已知︱x ︱=4，︱y ︱=5且x ＞y ，则2x-y 的值为（ ） A ．-13 B ．+13 C ．-3或+13 D ．+3或-1 6．下列说法正确的是( )A ．近似数1.50和1.5是相同的B ．3520精确到百位等于3600C ．6.610精确到千分位D ．2.708×104精确到千分位 7．下列算式中，计算结果是负数的是( ) A ．3(2)⨯- B ．|1|- C ．(2)7-+ D ．2(1)- 8．实数a ，b ，c ，d 在数轴上的位置如图所示，下列关系式不正确的是（ ）A ．|a|＞|b|B ．|ac|=acC ．b ＜dD ．c+d ＞0 9．下列说法中，正确的是（ ）A ．正数和负数统称有理数B ．既没有绝对值最大的数，也没有绝对值最小的数C ．绝对值相等的两数之和为零D ．既没有最大的数，也没有最小的数10．用计算器求243，第三个键应按（ ）A ．4B ．3C ．y xD ．=11．某种细菌在培养过程中，每半小时分裂一次（由一个分裂成两个）．经过3个小时，这种细菌由1个可分裂为（ ）A ．8个B ．16个C ．32个D ．64个 12．计算－3－1的结果是（ ）A ．2B ．－2C ．4D ．－4 13．当A 地高于海平面152米时，记作“海拔+152米”，那么B 地低于海平面23米时，记作（ ）A ．海拔23米B ．海拔﹣23米C ．海拔175米D ．海拔129米 14．甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（ ）A ．1℃~3℃B ．3℃~5℃C ．5℃~8℃D ．1℃~8℃ 15．下列分数不能化成有限小数的是（ ） A ．625 B ．324 C ．412 D ．116二、填空题16．若a 、b 、c 、d 、e 都是大于1、且是不全相等的五个整数，它们的乘积2000abcde =，则它们的和a b c d e ++++的最小值为__．17．23(2)0x y -++=，则x y 为______．18．3-的平方的相反数的倒数是___________.19．按下面程序计算，若开始输入x 的值为正数，最后输出的结果为656，则满足条件所有x 的值是___．20．数轴上A 、B 两点所表示的有理数的和是 ________.21．计算－32＋5－8×（－2）时，应该先算_____，再算_____，最后算_____．正确的结果为_____．22．如果点A 表示+3，将A 向左移动7个单位长度，再向右移动3个单位长度，则终点表示的数是__________．23．在数轴上，与表示-2的点的距离是4个单位的点所对应的数是___________. 24．如果数轴上原点右边 8 厘米处的点表示的有理数是 32，那么数轴上原点左边 12 厘米处的点表示的有理数是__________．25．一个数的25是165-，则这个数是______. 26．绝对值小于4.5的所有负整数的积为______．三、解答题27．计算：（1）4222(37)2(1)-+--⨯-； （2）157(36)2912⎛⎫-+⨯- ⎪⎝⎭．28．画一条数轴，把1-12，0，3各数和它们的相反数在数轴上表示出来，并比较它们的大小，用“<”号连接． 29．计算：(1)－8＋14－9＋20 (2)－72－5×(－2) 3＋10÷(1－2) 10 30．计算：329(1)4(2)34⎛⎫--÷-+-⨯ ⎪⎝⎭．。

七年级上册深圳西丽湖世纪星学校数学期末试卷培优测试卷一、初一数学上学期期末试卷解答题压轴题精选（难）1．数轴上A, B, C, D四点表示的有理数分别为1, 3, －5, －8（1）计算以下各点之间的距离：①A、B两点, ②B、C两点,③C、D两点,（2）若点M、N两点所表示的有理数分别为m、n，求M、N两点之间的距离．【答案】（1）AB=3-1=2；BC=3-（-5）=8；CD=-5-（-8）=-5+8=3.（2）MN=【解析】【分析】（1）数轴上两点间的距离等于数值较大的数减去数值较小的数，据此计算即可；（2）因为m、n的大小未知，则M、N两点间的距离为它们所表示的有理数之差的绝对值. 2．如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．（1）求出∠AOB及其补角的度数；（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由．【答案】（1）解：∠AOB=∠BOC+∠AOC=70°+50°=120°，其补角为180°-∠AOB=180°-120°=60°（2）解：∠DOC= ×∠BOC= ×70°=35°，∠AOE= ×∠AOC= ×50°=25°．∠DOE与∠AOB互补，理由：∵∠DOE=∠DOC+∠COE=35°+25°=60°，∴∠DOE+∠AOB=60°+120°=180°，故∠DOE与∠AOB互补【解析】【分析】（1）由∠BOC、∠AOC的度数，求出∠AOB=∠BOC+∠AOC的度数，再求出∠AOB补角的度数；（2）根据角平分线定义求出∠DOC、∠AOE的度数，再由（1）中的度数得到∠DOE与∠AOB互补.3．科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.（1）如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射出去，若b镜反射出的光线n平行于m，且∠1=30 ，则∠2=________，∠3=________；（2）在（1）中，若∠1=70 ，则∠3=________；若∠1=a，则∠3=________；（3）由（1）（2）请你猜想：当∠3=________时，任何射到平面镜a上的光线m经过平面镜a和b的两次反射后，入射光线m与反射光线n总是平行的？请说明理由.（提示：三角形的内角和等于180 ）【答案】（1）60°；90°（2）90°；90°（3）90°【解析】【解答】(1)∵入射角与反射角相等，即∠1=∠4，∠5=∠2，根据邻补角的定义可得根据m∥n,所以所以根据三角形内角和为所以故答案为：( 2 )由(1)可得∠3的度数都是( 3 )理由：因为所以又由题意知∠1=∠4，∠5=∠2，所以由同旁内角互补,两直线平行,可知：m∥n.【分析】（1）由入射角等于反射角可得∠1=∠4，∠5=∠2；由邻补角的定义可求得∠6的度数；于是由两直线平行，同旁内角互补可得∠6+∠7=则∠7的度数可求解，由图知∠5+∠7+∠2=所以∠5和∠2的度数可求解；再根据三角形的内角和等于可求得∠3的度数；（2）由（1）可知∠3=；（3）由（1）和（2）可得∠3=4．如图，在数轴上A点表示数a，B点表示数b，AB表示A点和B点之间的距离，C是AB的中点，且a、b满足|a+3|+（b+3a）2=0．（1）求点C表示的数；（2）点P从A点以3个单位每秒向右运动，点Q同时从B点以2个单位每秒向左运动，若AP+BQ=2PQ，求时间t；（3）若点P从A向右运动，点M为AP中点，在P点到达点B之前：① 的值不变；②2BM﹣BP的值不变，其中只有一个正确，请你找出正确的结论并求出其值．【答案】（1）解：∵|a＋3|＋(b＋3a)2＝0，∴a＋3＝0，b＋3a＝0，解得a＝﹣3，b＝9，∴＝3，∴点C表示的数是3（2）解：∵AB＝9－(－3)＝12，点P从A点以3个单位每秒向右运动，点Q同时从B点以2个单位每秒向左运动，∴AP＝3t，BQ＝2t，PQ＝12﹣5t．∵AP＋BQ＝2PQ，∴3t＋2t＝24﹣10t，解得t＝；还有一种情况，当P运动到Q的左边时，PQ＝5t﹣12，方程变为2t＋3t＝2（5t﹣12），求得t＝（3）解：∵PA＋PB＝AB为定值，PC先变小后变大，∴的值是变化的，∴①错误，②正确；∵BM＝PB＋，∴2BM＝2PB＋AP，∴2BM﹣BP＝PB＋AP＝AB＝12【解析】【分析】（1）根据非负数之和为，则每一个数都是0，建立关于a、b的二元一次方程组，解方程组求出a、b的值，再根据点C是AB的中点，因此点C表示的数为，列式计算可求出点C表示的数。

一、选择题1．若12a = ，3b =，且0a b <，则+a b 的值为（ ） A ．52 B ．52- C ．25± D ．52± 2．如果a ＝14-，b ＝－2，c ＝324-，那么︱a ︱+︱b ︱-︱c ︱等于（ ） A ．-12 B ．112 C ．12 D ．-1123．计算：11322⎛⎫⎛⎫-÷-÷- ⎪ ⎪⎝⎭⎝⎭的结果是（ ） A ．﹣3 B ．3C ．﹣12D ．12 4．在-1，2，-3，4，这四个数中，任意三数之积的最大值是（ ）A ．6B ．12C ．8D ．24 5．2--的相反数是（ ）A ．12-B ．2-C ．12D ．26．若1<a <2，则化简|a -2|+|1-a |的结果是（ ）A ．a -1B ．1C ．a +1D ．a -37．定义一种新运算2x y x y x+*=，如：2212122+⨯*==.则()(42)1**-=（ ） A ．1 B ．2 C ．0 D ．-28．已知a 、b 在数轴上的位置如图所示，将a 、b 、-a 、-b 从小到排列正确的一组是（ ）A ．-a <-b <a <bB ．-b <-a <a <bC ．-b <a <b <-aD ．a <-b <b <-a 9．若21(3)0a b -++=，则b a -=（ ）A ．-412B ．-212C ．-4D ．110．计算112123123412542334445555555555⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++---+++++⋯++⋯+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值（ ）A ．54B ．27C ．272D ．011．下列说法中，正确的是（）A．正数和负数统称有理数B．既没有绝对值最大的数，也没有绝对值最小的数C．绝对值相等的两数之和为零D．既没有最大的数，也没有最小的数12．如果|a|＝－a，下列成立的是()A．－a一定是非负数B．－a一定是负数C．|a|一定是正数D．|a|不能是013．绝对值大于1且小于4的所有整数的和是（）A．6 B．–6 C．0 D．4 14．2020年5月7日，世卫组织公布中国以外新冠确诊病例约为3504000例，把“3504000”用科学记数法表示正确的是（）A．3504×103B．3.504×106C．3.5×106D．3.504×107 15．6-的相反数是（）A．6 B．-6 C．16D．16-二、填空题16．3-的平方的相反数的倒数是___________.17．运用加法运算律填空：(1)[(－1)＋2]＋(－4)＝___＝___；(2)117＋(－44)＋(－17)＋14＝____＝____．18．一个班有45个人，其中45是_____数；大门约高1.90 m，其中1.90是_____数．19．校运动会的拔河比赛真是紧张刺激！规定拔河时，任意一方拉过30cm就算获胜．小胖他们班在每次喊过“拉”声之后都可拉过7cm，但又会被拉回3cm．如此下去，该班在第________次喊过“拉”声后就可获得胜利．20．阅读理解：根据乘方的意义，可得：22×23＝（2×2）×（2×2×2）＝25．请你试一试，完成以下题目：（1）a3•a4＝（a•a•a）•（a•a•a•a）＝__；（2）归纳、概括：a m•a n＝__；（3）如果x m＝4，x n＝9，运用以上的结论，计算：x m+n＝__．21．下列各组式子：①a﹣b与﹣a﹣b，②a+b与﹣a﹣b，③a+1与1﹣a，④﹣a+b与a ﹣b，互为相反数的有__．22．截至2020年7月2日，全球新冠肺炎确诊病例已超过1051万例，其中数据1051万用科学记数法表示为_____．23．下面是七年级一班在学校举行的足球赛中的成绩，现规定赢球为“正”，输球为“负”，打平为“0”，请按照示例填空：例：若上半场输了2个球，下半场输了1个球，则全场输了3个球，也就是(－2)＋(－1)＝－3；(1)若上半场赢了3个球，下半场输了2个球，则全场赢了____个球，也就是____；(2)若上半场输了3个球，下半场赢了2个球，则全场输了___个球，也就是_____；(3)若上半场赢了3个球，下半场打平，则全场赢了___个球，也就是____．24．在一次区级数学竞赛中，某校8名参赛学生的成绩与全区参赛学生平均成绩80分的差分别为(单位：分)：5，2-，8，14，7，5，9，6-，则该校8名参赛学生的平均成绩是______ ．25．已知0a >，0b <，b a >，比较a ，a -，b ，b -四个数的大小关系，用“<”把它们连接起来：_______．26．在数轴上，距离原点有2个单位的点所对应的数是________．三、解答题27．如图，数轴上A ，B 两点之间的距离为30，有一根木棒MN ，设MN 的长度为x ．MN 数轴上移动，M 始终在左，N 在右．当点N 移动到与点A ，B 中的一个重合时，点M 所对应的数为9，当点N 移动到线段AB 的中点时，点M 所对应的数是多少？28．计算：－32＋2×（－1）3－（－9）÷213⎛⎫ ⎪⎝⎭29．计算题：（1）3×（﹣4）﹣28÷（﹣7）；（2）﹣12020+（﹣2）3×1123⎛⎫-+ ⎪⎝⎭． 30．计算：（1）412115(2)5⎡⎤⎛⎫----⨯-÷- ⎪⎢⎥⎝⎭⎣⎦（2）1111243812⎛⎫÷-+- ⎪⎝⎭（要求简便方法计算）。

1．丁丁做了4道计算题：① 2018(1)2018-=；② 0(1)1--=-；③ 1111326-+-=；④11()122÷-=-请你帮他检查一下，他一共做对了（ ）道 A ．1道B ．2道C ．3道D ．4道A 解析：A【分析】根据乘方的意义以及有理数的减法、乘法、除法法则，有理数加减混合运算法则即可判断．【详解】①2018(1)1-=，故本小题错误；②0(1)1--=，故本小题错误； ③1113267-+-=-，故本小题错误； ④11()122÷-=-，正确； 所以，他一共做对了1题．故选A ．【点睛】本题考查了有理数的乘方、加法以及除法法则，熟练掌握运算法则是解题关键． 2．若b<0，刚a ，a+b ，a-b 的大小关系是（ ）A ．a<a <+b -b aB ．<a<a-b a+bC ．a<<a-b a+bD ．<a<a+b a-b D解析：D【分析】根据有理数减法法则，两两做差即可求解．【详解】∵b<0∴()0a a b b -+=->，()0a b a b --=->∴()a a b >+，()a b a ->∴()()a b a a b ->>+故选D ．【点睛】本题考查了有理数减法运算，减去一个负数等于加上这个数的相反数．3．如图是北京地铁一号线部分站点的分布示意图，在图中以正东为正方向建立数轴，有如下四个结论：①当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣3.5时，表示东单的点所表示的数为6；②当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣7时，表示东单的点所表示的数为12；③当表示天安门东的点所表示的数为1，表示天安门西的点所表示的数为﹣2.5时，表示东单的点所表示的数为7；④当表示天安门东的点所表示的数为2，表示天安门西的点所表示的数为﹣5时，表示东单的点所表示的数为14；上述结论中，所有正确结论的序号是（）A．①②③B．②③④C．①④D．①②③④D解析：D【分析】数轴上单位长度是统一的，利用图象，根据两点之间单位长度是否统一，判断即可．【详解】：①当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣3.5时，表示东单的点所表示的数为6，故①说法正确；②当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣7时，表示东单的点所表示的数为12，故②说法正确；③当表示天安门东的点所表示的数为1，表示天安门西的点所表示的数为﹣2.5时，表示东单的点所表示的数为7，故③说法正确；④当表示天安门东的点所表示的数为2，表示天安门西的点所表示的数为﹣5时，表示东单的点所表示的数为14，故④说法正确．故选：D．【点睛】本题考查了数轴表示数，数轴的三要素是：原点，正方向和单位长度，因此本题的关键是确定原点的位置和单位长度．4．2--的相反数是（）A．12-B．2-C．12D．2D解析：D【分析】|-2|去掉绝对值后为2，而-2的相反数为2．【详解】2--的相反数是2，故选：D．【点睛】本题考查了相反数和绝对值的概念，本题的关键是首先要对原题进行化简，然后在求这个数的相反数；其中，正数的相反数是负数，负数的相反数是正数，0的相反数是0．5．下列说法正确的是( )A．近似数1.50和1.5是相同的B．3520精确到百位等于3600C．6.610精确到千分位D．2.708×104精确到千分位C解析：C【分析】相似数和原值是不相同的；3520精确到百位是3500；2.708×104精确到十位．【详解】A、近似数1.50和1.5是不同的，A错B、3520精确到百位是3500，B错D、2.708×104精确到十位．【点睛】本题考察相似数的定义和科学计数法．6．2017年12月17日，第二架国产大型客机C919在上海浦东国际机场完成首次飞行．飞行时间两个小时，飞行的高度达到15000英尺．15000用科学记数法表示是（）A．0.15×105B．15×103C．1.5×104D．1.5×105C解析：C【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥1时，n是正数；当原数的绝对值＜1时，n是负数．【详解】15000用科学记数法表示是1.5×104．故选C．【点睛】本题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．7．下列各数中，互为相反数的是（）A．+(-2)与-2 B．+(+2)与-(-2) C．-(-2)与2 D．-|-2|与+(+2)D解析：D【解析】【分析】先将各选项中的数字化简，然后根据相反数的定义进行判断即可.【详解】A. +(-2)=-2，-2=-2，故A选项中的两个数不互为相反数；B. +(+2)=2， -(-2)=2，故B选项中的两个数不互为相反数；C. -(-2)=2，2=2，故C选项中的两个数不互为相反数；D. -|-2|=-2，+(+2)=2，-2与2互为相反数，故D选项中的两个数互为相反数，故选D.【点睛】本题考查了相反数的概念，涉及了绝对值化简等，熟练掌握相关知识是解题的关键.8．计算11212312341254 2334445555555555⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++---+++++⋯++⋯+⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值（）A．54 B．27 C．272D．0C解析：C【分析】根据有理数的加减混合运算先算括号内的，进而即可求解．【详解】解：原式＝﹣12+1﹣32+2﹣52+3﹣72+…+27＝27×1 2＝272．故选：C．【点睛】本题考查了有理数的加减混合运算，解决本题的关键是寻找规律．9．将(－3.4)3，(－3.4)4，(－3.4)5从小到大排列正确的是()A．(－3.4)3＜(－3.4)4＜(－3.4)5B．(－3.4)5＜(－3.4)4＜(－3.4)3C．(－3.4)5＜(－3.4)3＜(－3.4)4D．(－3.4)3＜(－3.4)5＜(－3.4)4C解析：C【解析】(－3.4)3、 (－3.4)5的积为负数，且(－3.4)3的绝对值小于 (－3.4)5的绝对值，所以(－3.4)3>(－3.4)5；(－3.4)4的积为正数，根据正数大于负数，即可得(－3.4)5＜(－3.4)3＜(－3.4)4，故选C.10．如果用＋0.02克表示一只乒乓球质量超出标准质量0.02克，那么一只乒乓球质量低于标准质量0.02克记作（）.A．＋0.02克B．－0.02克C．0克D．＋0.04克B解析：B【解析】－0.02克，选A.11．计算－3－1的结果是（ ）A ．2B ．－2C ．4D ．－4D 解析：D【解析】试题-3-1=-3+（-1）=-（3+1）=-4．故选D.12．一根1米长的绳子，第一次剪去一半，第二次剪去剩下的一半，如此下去，第六次后剩下的绳子长度为（ ）A ．312⎛⎫ ⎪⎝⎭米B ．512⎛⎫ ⎪⎝⎭米C ．612⎛⎫ ⎪⎝⎭米D ．1212⎛⎫ ⎪⎝⎭米C 解析：C【分析】 根据乘方的意义和题意可知：第2次后剩下的绳子的长度为(12)2米，那么依此类推得到第六次后剩下的绳子的长度为(12)6米． 【详解】∵1-12=12， ∴第2次后剩下的绳子的长度为(12)2米； 依此类推第六次后剩下的绳子的长度为(12)6米． 故选C ．【点睛】此题主要考查了乘方的意义．其中解题是正确理解题意是解题的关键，能够根据题意列出代数式是解题主要步骤．13．若1＜x ＜2，则|2||1|||21x x x x x x ---+--的值是（ ） A ．﹣3B ．﹣1C ．2D ．1D 解析：D【分析】在解绝对值时要考虑到绝对值符号中代数式的正负性，再去掉绝对值符号．【详解】解：12x <<，20x ∴-<，10x ->，0x >，∴原式1111=-++=，故选：D ．【点睛】本题主要考查了绝对值，代数式的化简求值问题．解此题的关键是在解绝对值时要考虑到绝对值符号中代数式的正负性，再去掉绝对值符号．14．计算－2的结果是（ ） A ．0B ．－2C ．－4D ．4A 解析：A【详解】解：因为|-2|－2=2-2=0，故选A ．考点：绝对值、有理数的减法15．若2020M M +-＝+，则M 一定是（ ）A ．任意一个有理数B ．任意一个非负数C ．任意一个非正数D ．任意一个负数B 解析：B【分析】直接利用绝对值的性质即可解答．【详解】解：∵M ＋｜-20｜＝｜M ｜＋｜20｜，∴Ｍ≥0，为非负数．故答案为B ．【点睛】本题考查了绝对值的应用，灵活应用绝对值的性质是正确解答本题的关键．1．绝对值小于2的整数有_______个，它们是______________.3;－101等【分析】当一个数为非负数时它的绝对值是它本身；当这个数是负数时它的绝对值是它的相反数【详解】绝对值小于2的整数包括绝对值等于0的整数和绝对值等于1的整数它们是0±1共有3个故答案为(1解析：3; －1，0，1等.【分析】当一个数为非负数时，它的绝对值是它本身；当这个数是负数时，它的绝对值是它的相反数．【详解】绝对值小于2的整数包括绝对值等于0的整数和绝对值等于1的整数，它们是0，±1，共有3个．故答案为(1). 3; (2). －1，0，1等．【点睛】本题考查了绝对值，熟悉掌握绝对值的定义是解题的关键．2．数轴上，如果点 A 所表示的数是3-,已知到点 A 的距离等于 4 个单位长度的点所表示的数为负数，则这个数是_______．-7【分析】根据在数轴上点A 所表示的数为3可以得到到点A的距离等于4个单位长度的点所表示的数是什么再根据负数的定义即可求解【详解】解：∵点A所表示的数是-3到点A的距离等于4个单位长度的点所表示的数解析：-7【分析】根据在数轴上，点A所表示的数为3，可以得到到点A的距离等于4个单位长度的点所表示的数是什么，再根据负数的定义即可求解．【详解】解：∵点A所表示的数是-3，到点A的距离等于4个单位长度的点所表示的数为负数，∴这个数是-3-4=-7．故答案为：-7．【点睛】本题考查了数轴，解题的关键是明确数轴的特点，知道到一个点的距离等3个单位长度的点表示的数有两个．3．已知|a|＝3，|b|＝2，且ab＜0，则a﹣b＝_____．5或﹣5【分析】先根据绝对值的定义求出ab的值然后根据ab＜0确定ab的值最后代入a﹣b中求值即可【详解】解：∵|a|＝3|b|＝2∴a＝±3b＝±2；∵ab＜0∴当a＝3时b＝﹣2；当a＝﹣3时b解析：5或﹣5【分析】先根据绝对值的定义，求出a、b的值，然后根据ab＜0确定a、b的值，最后代入a﹣b中求值即可．【详解】解：∵|a|＝3，|b|＝2，∴a＝±3，b＝±2；∵ab＜0，∴当a＝3时b＝﹣2；当a＝﹣3时b＝2，∴a﹣b＝3﹣（﹣2）＝5或a﹣b＝﹣3﹣2＝﹣5．故填5或﹣5．【点睛】本题主要考查的是有理数的乘法、绝对值、有理数的减法，熟练掌握相关法则是解题的关键．4．数轴上A、B两点所表示的有理数的和是 ________.-1【解析】由数轴得点A表示的数是﹣3点B表示的数是2∴AB两点所表示的有理数的和是﹣3+2=﹣1故答案为-1解析：-1【解析】由数轴得，点A表示的数是﹣3，点B表示的数是2，∴ A，B两点所表示的有理数的和是﹣3+2=﹣1，故答案为-1.5．绝对值不大于2.1的所有整数是____，其和是____．﹣2﹣10120【分析】找出绝对值不大于21的所有整数求出之和即可【详解】绝对值不大于21的所有整数有﹣2﹣1012之和为﹣2﹣1+0+1+2=0故答案为：﹣2﹣1012；0【点评】此题考查了绝对值解析：﹣2，﹣1，0，1，2 0【分析】找出绝对值不大于2.1的所有整数，求出之和即可．【详解】绝对值不大于2.1的所有整数有﹣2、﹣1、0、1、2，之和为﹣2﹣1+0+1+2=0，故答案为：﹣2，﹣1，0，1，2；0【点评】此题考查了绝对值的意义和有理数的加法，熟练掌握运算法则是解本题的关键．6．计算－32＋5－8×（－2）时，应该先算_____，再算_____，最后算_____．正确的结果为_____．乘方乘法加法12【分析】按照有理数混合运算的运算顺序进行计算解答即可【详解】解：原式=-9+5+16=12故答案为：乘方乘法加法12【点睛】本题主要考查了有理数混合运算的运算顺序先算乘方再算乘除最后解析：乘方乘法加法12【分析】按照有理数混合运算的运算顺序进行计算解答即可.【详解】解：原式=-9+5+16=12.故答案为：乘方，乘法，加法，12【点睛】本题主要考查了有理数混合运算的运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的.7．校运动会的拔河比赛真是紧张刺激！规定拔河时，任意一方拉过30cm就算获胜．小胖他们班在每次喊过“拉”声之后都可拉过7cm，但又会被拉回3cm．如此下去，该班在第________次喊过“拉”声后就可获得胜利．7【分析】根据题意得到当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取得胜利【详解】解：由题意得喊过一次拉声之后可拉过当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取解析：7【分析】⨯-=，离胜利还差根据题意得到当喊到第6次时，一共拉过了6(73)24(cm)-=，所以再喊一次后拉过7cm，超过了30cm，即可取得胜利.30246(cm)【详解】解：由题意得喊过一次“拉”声之后可拉过4cm.⨯-=.当喊到第6次时，一共拉过了6(73)24(cm)-=，离胜利还差30246(cm)所以再喊一次后拉过7cm，超过了30cm，即可取得胜利.故答案为:7.【点睛】此题考查了有理数的混合运算的应用，正确理解题意，掌握有理数的各运算法则是解题的关键.8．等边三角形ABC（三条边都相等的三角形是等边三角形）在数轴上的位置如图所示，-，若ABC绕着顶点顺时针方向在数轴上翻转1次后，点A，B对应的数分别为0和1点C所对应的数为1，则再翻转3次后，点C所对应的数是________．4【分析】结合数轴不难发现每3次翻转为一个循环组依次循环然后进行计算即可得解【详解】根据题意可知每3次翻转为一个循环∴再翻转3次后点C在数轴上∴点C对应的数是故答案为：4【点睛】本题考查了数轴及数的解析：4【分析】结合数轴不难发现，每3次翻转为一个循环组依次循环，然后进行计算即可得解．【详解】根据题意可知每3次翻转为一个循环，∴再翻转3次后，点C在数轴上，+⨯=．∴点C对应的数是1134故答案为：4.【点睛】本题考查了数轴及数的变化规律，根据翻转的变化规律确定出每3次翻转为一个循环组依次循环是解题的关键．9．一个跳蚤在一条数轴上，从0开始，第1次向右跳1单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，依此规律下去，当它跳第100落下时，落点在数轴上表示的数是_________ .-50【分析】根据题意列出式子然后计算即可【详解】根据题意落点在数轴上表示的数是0＋1－2＋3－4＋ (99)100=（1－2）＋（3－4）＋……＋（99－100）===-50故答案为：-50【点解析：-50【分析】根据题意,列出式子,然后计算即可．【详解】根据题意,落点在数轴上表示的数是0＋1－2＋3－4＋……＋99－100=（1－2）＋（3－4）＋……＋（99－100）=()()()10021111÷--+-+-个=150-⨯=-50故答案为：-50．【点睛】此题考查的是有理数的加减法的应用，掌握有理数的加、减法法则和加法结合律是解决此题的关键．10．A ，B ，C 三地的海拔高度分别是50-米，70-米，20米，则最高点比最低点高______米．90【分析】先根据有理数的大小比较法则得出最高点和最低点再列出运算式子计算有理数的减法即可得【详解】因为所以最高点的海拔高度为20米最低点的海拔高度米则（米）即最高点比最低点高90米故答案为：90【解析：90【分析】先根据有理数的大小比较法则得出最高点和最低点，再列出运算式子，计算有理数的减法即可得．【详解】因为205070>->-，所以最高点的海拔高度为20米，最低点的海拔高度70-米，则20(70)207090--=+=（米），即最高点比最低点高90米，故答案为：90．【点睛】本题考查了有理数的大小比较法则、有理数减法的实际应用，依据题意，正确列出运算式子是解题关键．11．已知2x =，3y =，且x y <，则34x y -的值为_______．-6或-18【分析】先依据绝对值的性质求得xy 的值然后再代入计算即可【详解】解：∵∴∵∴当x=2y=3时；当x=-2y=3时故答案为：-6或-18【点睛】此题考查了有理数的混合运算以及绝对值熟练掌握解析：-6或-18【分析】先依据绝对值的性质求得x 、y 的值，然后再代入计算即可．【详解】解：∵2x =，3y =，∴2x =±，3=±y ．∵x y <，∴2x =±，3y =，当x=2，y=3时，346x y -=-；当x=-2，y=3时，3418x y -=-．故答案为：-6或-18．【点睛】此题考查了有理数的混合运算以及绝对值，熟练掌握绝对值的代数意义是解本题的关键． 1．计算（1）112(24)243⎛⎫-⨯-+- ⎪⎝⎭； （2）3221(2)(3)⎡⎤÷---⎣⎦；（3）2202035|5|(1)( 3.14)02π⎛⎫---⨯-+-⨯ ⎪⎝⎭． 解析：（1）22；（2）2117-；（3）54-． 【分析】（1）原式利用乘法分配律计算即可得到结果；（2）原式先计算乘方运算，再计算括号内的运算，最后除法运算即可得到结果； （3）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；【详解】 （1）112(24)243⎛⎫-⨯-+- ⎪⎝⎭ 112(24)(24)(24)243⎛⎫⎛⎫=-⨯-+-⨯+-⨯- ⎪ ⎪⎝⎭⎝⎭12616=-+=22；（2）3221(2)(3)⎡⎤÷---⎣⎦()2189=÷--()2117=÷-2117=-； （3）2202035|5|(1)( 3.14)02π⎛⎫---⨯-+-⨯ ⎪⎝⎭ 255104=-⨯+54=-． 【点睛】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．2．（1）371(24)812⎛⎫-+⨯- ⎪⎝⎭；（2）431(2)2(3)----⨯- 解析：（1）-29；（2）13．【分析】（1）利用乘法分配律进行简便运算，即可得出结果；（2）先计算有理数的乘方与乘法，再进行加减运算即可．【详解】解：（1）371(24)812⎛⎫-+⨯- ⎪⎝⎭ 37(1242424)812=-⨯-⨯+⨯ (24914)=--+29=-；（2）431(2)2(3)----⨯-1(8)(6)=-----186=-++13=．【点睛】本题考查了有理数的混合运算，熟练掌握有理数混合运算的运算顺序、运算法则及乘法运算律是解题的关键．3．设0a >，x ，y 为有理数，定义新运算：||a x a x =⨯※．如323|2|6=⨯=※，()414|1|a a -=⨯-※．（1）计算20210※和()20212-※的值． （2）若0y <，化简()23y -※．（3）请直接写出一组,,a x y 的具体值，说明()a x y a x a y +=+※※※不成立． 解析：（1）0；4042；(2)6y -；（3）1a =，2x =，3y =-（答案不唯一）【分析】(1)根据题意※表示前面的数与后面数的绝对值的积，直接代入数据求解计算；(2)有y<0，得到y 为负数，进而得到-3y 为正数，去绝对值后等于本身-3y ，再代入数据求解即可；(3)按照题意要求写一组具体的,,a x y 的值再验算即可．【详解】解：(1)根据题意得:202102021|0|0=⨯=※；()202122021|2|4042-=⨯-=※；(2)因为0y <，所以30y ->，所以()()232|3|236y y y y -=⨯-=⨯-=-※；(3)由题意，当,,a x y 分别取1a =，2x =，3y =-时，此时()2311※※(-1)=1-=，而11※2※(-3)=2+3=5+，所以，()a x y a x a y +=+※※※不成立．【点睛】本题是新定义题型，按照题目中给定的运算要求和顺序进行求解即可．4．给出四个数：3,4--,2,6，计算“24点”，请列出四个符合要求的不同算式． （可运用加、减、乘、除、乘方运算，可用括号；注意：例如4(123)24⨯++=与(213)424++⨯=只是顺序不同，属同一个算式．）算式1：_________________；算式2_______________；算式3：_________________；算式4_______________；解析：()()342624,-⨯-+⨯=()()342624,-⨯-+-=()()643224,⨯-⨯-+=()()()()43624624.-⨯--÷=-⨯-=【分析】由241212,=+ 可得()342624,-⨯-+⨯=由()2438=-⨯-，可得()()342624,-⨯-+-=由()24124,=-⨯- 可得()()643224,⨯-⨯-+=由()2446=-⨯-，可得()()()()43624624-⨯--÷=-⨯-=，从而可得答案．【详解】解：算式1：()()3426121224,-⨯-+⨯=+=算式2：()()()()34263824,-⨯-+-=-⨯-=算式3：()()()()643224124,⨯-⨯-+=-⨯-=算式4：()()()()()()43624334624,-⨯--÷=-⨯--=-⨯-=故答案为：()()342624,-⨯-+⨯=()()342624,-⨯-+-=()()643224,⨯-⨯-+=()()()()43624624.-⨯--÷=-⨯-=【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法，注意本题答案不唯一，这是一道开放性的题目，同时考查了学生的逆向思维．。

深圳西丽湖世纪星学校数学分式填空选择单元培优测试卷一、八年级数学分式填空题（难）1．如果我们定义()1x f x x =+，(例如：()555)156f ==+，试计算下面算式的值：1120152f f ⎛⎫⎛⎫+⋯+ ⎪ ⎪⎝⎭⎝⎭ ()()()()101220151f f f f f ⎛⎫++++⋯+= ⎪⎝⎭______ ． 【答案】2015 【解析】 【分析】根据题意得出规律f （x ）+f （1x）=1，原式结合后计算即可得到结果． 【详解】解：f （x ）+f （1x ）=x 1x ++111x x+=11x x ++=1， 则原式=[f （12015）+f （2015）]+…+[f （12）+f （2）]+[f （11）+f （1）]+f （0）=2015， 故答案为：2015． 【点睛】此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．2．当m= __________ 时，关于x 的分式方程231062x m x x x +++=--+没有实数解. 【答案】4或-6 【解析】 【分析】先将分式方程化为整式方程，根据方程231062x m x x x +++=--+没有实数解会产生增根判断增根是x=3或x=-2，再把增根x=3或x=-2代入整式方程即可求出m 的值． 【详解】 解：方程231062x m x x x +++=--+变形为310(3)(2)2x m x x x +++=-++， 方程两边同时乘以(3)(2)x x -+去分母得：x+m+3+x-3=0； 整理得：2x+m=0∵关于x 的分式方程231062x m x x x +++=--+没有实数解. ∴分式方程有增根x=3或x=-2.把x=3和x=-2分别代入2x+m=0中得m=-6或m=4. 【点睛】分式方程无解问题或增根问题可按如下步骤进行：①根据最简公分母确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．但也要注意，有时分式方程转化成的整式方程本身没有实数根，也是导致分式方程没有实数根的一种情况，所以要考虑全面，免得漏解.3．函数y =x 的取值范围是______． 【答案】23x -<≤ 【解析】 【分析】根据二次根式及分式有意义的条件，结合所给式子得到关于x 的不等式组，解不等式组即可求出x 的取值范围． 【详解】由题意得，30200x x ⎧-≥⎪+≥⎨≠，解得：-2<x≤3， 故答案为：-2<x≤3. 【点睛】本题考查了二次根式及分式有意义的条件，注意掌握二次根式有意义：被开方数为非负数，分式有意义分母不为零．4．如果x+1x ＝3，则24233x x x ++的值等于_____ 【答案】122【解析】 【分析】由x +1x =3得x 2+2+21x =9，即x 2+21x=7，整体代入原式=221331x x ++=221131x x ++（），计算可得结论． 【详解】解：∵x +1x =3，∴（x +1x ）2=9，即x 2+2+21x =9，则x 2+21x=7．∵x ≠0，∴原式=221331x x ++=221131x x ++（） =1371⨯+ =122． 故答案为122． 【点睛】本题主要考查分式的值，解题的关键是熟练掌握整体代入思想的运用及利用分式的基本性质对分式变形．5．已知x 为正整数，当时x=________时，分式62x-的值为负整数． 【答案】3、4、5、8 【解析】由题意得：2﹣x ＜0，解得x ＞2，又因为x 为正整数，讨论如下： 当x=3时， 62x-=﹣6，符合题意； 当x=4时， 62x-=﹣3，符合题意； 当x=5时， 62x-=﹣2，符合题意； 当x=6时， 62x -=﹣32，不符合题意，舍去； 当x=7时， 62x -=﹣65，不符合题意，舍去； 当x=8时，62x-=﹣1，符合题意； 当x≥9时，﹣1＜62x-＜0，不符合题意．故x 的值为3，4，5，8． 故答案为：3、4、5、8．6．若关于x 的分式方程x 2322m mx x++=--的解为正实数，则实数m 的取值范围是____．【答案】m ＜6且m≠2. 【解析】 【分析】利用解分式方程的一般步骤解出方程，根据题意列出不等式，解不等式即可． 【详解】x 2322m mx x++=--， 方程两边同乘（x-2）得，x+m-2m=3x-6， 解得，x=6-2m， 由题意得，6-2m＞0， 解得，m ＜6，∵6-2m≠2， ∴m≠2，∴m＜6且m≠2. 【点睛】要注意的是分式的分母暗含着不等于零这个条件，这也是易错点．7．化简a b b a a b+--的结果是______ 【答案】﹣1 【解析】分析：直接利用分式加减运算法则计算得出答案．详解：a b b a a b +--=a b b a b a ---=()1a b b a b a b a ---==---． 故答案为-1．点睛：此题主要考查了分式的加减运算，正确掌握运算法则是解题关键．8．若关于x 的分式方程7311mx x x +=--无解，则实数m =_______． 【答案】3或7． 【解析】解：方程去分母得：7+3（x ﹣1）=mx ，整理得：（m ﹣3）x =4．①当整式方程无解时，m ﹣3=0，m =3；②当整式方程的解为分式方程的增根时，x =1，∴m ﹣3=4，m =7． 综上所述：∴m 的值为3或7． 故答案为3或7．9．若22440,x yx xy y x y--+=+则等于________． 【答案】13【解析】解：∵x 2﹣4xy +4y 2=0，∴（x ﹣2y ）2=0，∴x =2y ，∴x y x y -+=22y y y y -+=13．故答案为13． 点睛：根据已知条件x 2﹣4xy +4y 2=0，求出x 与y 的关系是解答本题的关键．10．小明到商场购买某个牌子的铅笔x 支，用了y 元（y 为整数）．后来他又去商场时，发现这种牌子的铅笔降价20%，于是他比上一次多买了10支铅笔，用了4元钱，那么小明两次共买了铅笔________支． 【答案】40或90 【解析】 【分析】因y 元买了x 只铅笔，则每只铅笔y x 元；降价20%后，每只铅笔的价格是45yx元，依题意得45yx（x+10）=4，变形可得x=105y y -，即可得y ＜5；再由x 、y 均是正整数，确定y 只能取3或4，由此求得x 的值，即可得小明两次所买铅笔的数量. 【详解】因y 元买了x 只铅笔，则每只铅笔y x 元；降价20%后，每只铅笔的价格是 （1-20%）yx元，即45y x 元，依题意得：45yx（x+10）=4， ∴y （x+10）=5x∴x=105y y-，∴5-y ＞0，即y ＜5； 又∵x 、y 均是正整数， ∴y 只能取3和4；①当y=3时， x=15，小明两次共买了铅笔：15+15+10=40（支） ②当y=4时， x=40，小明两次共买了铅笔：40+（40+10）=90（支） 故答案为40或90． 【点睛】本题考查了方程的应用，解决根据题意列出方程45yx（x+10）=4确定x 、y 的值是解决问题的关键.二、八年级数学分式解答题压轴题（难）11．某开发公司生产的 960 件新产品需要精加工后，才能投放市场，现甲、乙两个工厂都想加工这批产品，已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20 天，而甲工厂每天加工的数量是乙工厂每天加工的数量的23，公司需付甲工厂加工费用为每天 80 元，乙工厂加工费用为每天 120 元．（1）甲、乙两个工厂每天各能加工多少件新产品？（2）公司制定产品加工方案如下：可以由每个厂家单独完成，也可以由两个厂家合作完成．在加工过程中，公司派一名工程师每天到厂进行技术指导，并负担每天 15 元的午餐补助费，请你帮公司选择一种既省时又省钱的加工方案，并说明理由．【答案】（1）甲工厂每天加工 16 件产品，乙工厂每天加工 24 件产品. （2）甲、乙两工厂合作完成此项任务既省时又省钱．见解析．【解析】【分析】（1）设甲工厂每天加工 x 件新品，乙工厂每天加工 1.5x 件新品，根据题意找出等量关系：甲厂单独加工这批产品所需天数﹣乙工厂单独加工完这批产品所需天数＝20，由等量关系列出方程求解．（2）分别计算出甲单独加工完成、乙单独加工完成、甲、乙合作完成需要的时间和费用，比较大小，选择既省时又省钱的加工方案即可．【详解】（1）设甲工厂每天加工 x 件新品，乙工厂每天加工 1.5x 件新品，则：解得：x＝16经检验，x＝16 是原分式方程的解∴甲工厂每天加工 16 件产品，乙工厂每天加工 24 件产品（2）方案一：甲工厂单独完成此项任务，则需要的时间为：960÷16＝60 天需要的总费用为：60×（80+15）＝5700 元方案二：乙工厂单独完成此项任务，则需要的时间为：960÷24＝40 天需要的总费用为：40×（120+15）＝5400 元方案三：甲、乙两工厂合作完成此项任务，设共需要 a 天完成任务，则16a+24a＝960∴a＝24∴需要的总费用为：24×（80+120+15）＝5 160 元综上所述：甲、乙两工厂合作完成此项任务既省时又省钱．【点睛】本题主要考查分式方程的应用，解题的关键在于理解清楚题意，找出等量关系，列出方程求解．需要注意：①分式方程求解后，应注意检验其结果是否符合题意；②选择最优方案时，需将求各个方案所需时间和所需费用，经过比较后选择最优的那个方案．12．按要求完成下列题目．()1求：()11111223341n n +++⋯+⨯⨯⨯+的值． 对于这个问题，可能有的同学接触过，一般方法是考虑其中的一般项，注意到上面和式的每一项可以写成()11n n +的形式，而()11111n n n n =-++，这样就把()11n n +一项(分)裂成了两项．试着把上面和式的每一项都裂成两项，注意观察其中的规律，求出上面的和，并直接写出111112233420162017+++⋯+⨯⨯⨯⨯的值． ()2若()()()()()112112A Bn n n n n n n =++++++①求：A 、B 的值：②求：()()11112323412n n n ++⋯+⨯⨯⨯⨯++的值． 【答案】()()()3412n n n n +++【解析】 【分析】（1）根据题目的叙述的方法即可求解；（2）①把等号右边的式子通分相加，然后根据对应项的系数相等即可求解；②根据()()()()()11111..1221212n n n n n n n =-+++++把所求的每个分式化成两个分式的差的形式，然后求解． 【详解】 解：（1）112⨯+123⨯+134⨯+…+120161017⨯ =1-12+12-13+13-14+…+12016-12017=1-12017 =20162017； （2）①∵()1A n n ++()()12B n n ++=()()()2n 12A B n An n ++++=()()1n 12n n ++，∴120A B B ⎧=⎪⎨⎪+=⎩， 解得1212A B ⎧=⎪⎪⎨⎪=-⎪⎩． ∴A 和B 的值分别是12和-12； ②∵()()1n 12n n ++=12•()11n n +-12•()()1n 12n n ++=12•（1n -1n 1+）-12（11n +-12n +）∴原式=12•112⨯-12•123⨯+12•123⨯-12•134⨯+…+12•()11n n +-12•()()112n n ++=12•112⨯-12•()()112n n ++ =14-()()1212n n ++=()()()3412n n n n +++．【点睛】本题考查了分式的化简求值，正确理解()()1n 12n n ++=12•()1n 1n +-12•()()112n n ++是关键．13．为进一步落实《中华人民共和国民办教育促进法》，某市教育局拿出了b 元资金建立民办教育发展基金会，其中一部分作为奖金发给了n 所民办学校．奖金分配方案如下：首先将n 所民办学校按去年完成教育、教学工作业绩（假设工作业绩均不相同）从高到低，由1到n 排序，第1所民办学校得奖金bn元，然后再将余额除以n 发给第2所民办学校，按此方法将奖金逐一发给了n 所民办学校．（1）请用n 、b 分别表示第2所、第3所民办学校得到的奖金；（2）设第k 所民办学校所得到的奖金为k a 元（1k n ≤≤），试用k 、n 和b 表示k a （不必证明）；（3）比较k a 和1k a +的大小（k=1，2 ，……，1n -），并解释此结果关于奖金分配原则的实际意义．【答案】（1）211()(1)b b a b n n n n =-⨯=- ,23111()(1)(1)b b a b n n n n n=-⨯-=-； （2）11(1)k k ba nn-=- ； （3）1k k a a +> ．奖金分配的实际意义：名次越靠后，奖金越少． 【解析】 【试题分析】（1）根据第1所民办学校得奖金bn元，然后再将余额除以n 发给第2所民办学校，得：22311111()(1),()(1)(1).b b b b a b a b n n n n n n n n n=-⨯=-=-⨯-=- （2）根据（1）中的两个式子，11(1)k k b a nn-=- ； （3）11(1)k k b a nn -=-，+11(1)k k b a n n=-，则1111+121111111(1)(1)(1)1(1)(1)(1)0k k k k k k k b b b b ba a n n n n n n n n n n n n----⎡⎤-=---=---=-⋅⋅=-⋅>⎢⎥⎣⎦，则+1k k a a >.奖金分配的实际意义：名次越靠后，奖金越少.【试题解析】（1）根据题意得：22311111()(1),()(1)(1).b b b b a b a b n n n n n n n n n=-⨯=-=-⨯-=- （2）根据（1）中的两个式子，11(1)k k b a nn-=- （3）11(1)k k b a nn -=-，+11(1)k k b a n n=-，则1111+121111111(1)(1)(1)1(1)(1)(1)0k k k k k k k b b b b ba a n n n n n n n n n n n n----⎡⎤-=---=---=-⋅⋅=-⋅>⎢⎥⎣⎦，则+1k k a a >.奖金分配的实际意义：名次越靠后，奖金越少.【方法点睛】本题目是一道分式的实际应用问题，第一个问题有难度，依据奖金的分配规则，写出23a a 、 的表达式；第二问在第一问的基础上，找出规律，直接写出k a 的表达式即可；第三问用作差法比较两个分式的大小，若差为正数，则被减数大于减数；若差为0，则被减数等于减数；若差为负数，则被减数小于减数.14．（1）请你写出五个正的真分数，____，____，____，____，____，给每个分数的分子和分母加上同一个正数得到五个新分数：____，____，____，_____，____. （2）比较原来每个分数与对应新分数的大小，可以得出下面的结论：一个真分数是a b （a 、b 均为正数），给其分子分母同加一个正数m ，得a m b m ++，则两个分数的大小关系是a mb m ++_____ab. （3）请你用文字叙述（2）中结论的含义： （4）你能用图形的面积说明这个结论吗？（5）解决问题：如图1，有一个长宽不等的长方形绿地，现给绿地四周铺一条宽相等的路，问原来的长方形与现在铺过小路后的长方形是否相似？为什么？（6）这个结论可以解释生活中的许多现象，解决许多生活与数学中的问题.请你再提出一个类似的数学问题，或举出一个生活中与此结论相关例子. 【答案】(1)12；14；16；18；19；23；25；27；29；15；（2）＞；（3）给一个正的真分数的分子、分母同加一个正数，得到的新分数大于原来的分数；（4）答案见解析；（5）不相似，理由见解析；（6）答案见解析. 【解析】 【分析】（1）小于1的数叫做真分数；（2）根据实例易得规律；（3）抓住新分数大于原分数即可；（4）根据图形进行分析解答；（5）利用相关规律解决问题即可；（6）结合生活中的现象进行解答. 【详解】 解：（1）12、14、16、18、19，23、25、27、29、15；（2）a m ab m b+>+； （3）给一个正的真分数的分子、分母同加一个正数，得到的新分数大于原来的分数； （4）思路1：如图2所示，由a b <，得12s s s s +>+，即ab bm ab am +>+，()().a b m b a m +=+，可推出a m ab m b+>+；思路2：构造两个面积为1的长方形（如图3），将它们分成两部分，比较右侧的两个长方形面积可以发现：1a b a b b --=，1a m b a b m b m+--=++，因为a 、b 、0m >，且a b <，故1a b - 1a m b m +>-+，即a m a b m b+>+ （5）不相似.因为两个长方形长与宽的比值不相等；（6）数学问题举例：①若a b是假分数，会有怎样的结论？ ②a 、b 不是正数，或不全是正数，情况如何？【点睛】本题实际考查了分式的基本性质，熟练掌握分式的基本性质是解题的关键.15．水蜜桃是无锡市阳山的特色水果，水蜜桃一上市，水果店的老板用2000元购进一批水密桃，很快售完；老板又用3300元购进第二批水蜜桃，所购件数是第一批的32倍，但进价比第一批每件多了5元．（1）第一批水蜜桃每件进价是多少元？（2）老板以每件65元的价格销售第二批水蜜桃，售出80％后，为了尽快售完，剩下的决定打折促销．要使得第二批水密桃的销售利润不少于288元，剩余的仙桃每件售价最多打几折？(利润=售价-进价)【答案】（1）50；（2）6折．【解析】【分析】（1）根据题意设第一批水蜜桃每件进价是x 元，利用第二批水密桃进价建立方程求解即可；（2）根据题意设剩余的仙桃每件售价最多打m 折，并建立不等式，求出其解集即可得出剩余的仙桃每件售价最多打几折.【详解】解：（1）设第一批水蜜桃每件进价是x 元，则有：20003(5)33002x x ⨯⨯+=，解得50x =， 所以第一批水蜜桃每件进价是50元.（2）由（1）得出第二批水密桃的进价为：55元，数量为：33006055=件， 设剩余的仙桃每件售价最多打m 折，则有： 6580606065(180)3300288m ⨯⨯+⨯⨯--≥％％，解得0.6m ≥，即最多打6折.【点睛】本题考查分式方程的实际应用以及不等式的实际应用，理解题意并根据题意建立方程和不等式是解题的关键.。