机械原理 西工大第八版第4章 平面机构的力分析

第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标，其定义为在不考虑摩擦的条件下机构的输出力（力矩）与输入力（力矩）之比值，即Δ=d r d r F F M M //=。

试求图示各机构在图示位置时的机械效益。

图a 所示为一铆钉机，图b 为一小型压力机，图c 为一剪刀。

计算所需各尺寸从图中量取。

（a ） (b) (c)解：(a)作铆钉机的机构运动简图及受力 见下图（a ）由构件3的力平衡条件有：02343=++R R rF F F由构件1的力平衡条件有：04121=++d R R按上面两式作力的多边形见图（b ）得θcot ==∆d r F F（b ）作压力机的机构运动简图及受力图见（c ）由滑块5的力平衡条件有：04565=++R R F F G由构件2的力平衡条件有：0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图（d ），得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。

tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中，设已知l AB=0.1m，l BC=0.33m，n1=1500r/min（为常数），活塞及其附件的重量G3=21N，连杆质量G2=25N，J S2=0.0425kg·m2，连杆质心S2至曲柄销B的距离l BS2=l BC/3。

试确定在图示位置时活塞的惯性力以及连杆的总惯性力。

解：1) 选定比例尺, mmml005.0=μ绘制机构运动简图。

(图(a) )2）运动分析：以比例尺vμ作速度多边形，如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3：)(37673333NagGamFCSI=-=-=方向与cp''相反。

机械原理平面机构的力分析机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。

平面机构是平面运动副的组合，由多个刚体构成，通过运动副连接起来的，因此需要进行力学分析来了解各个部件之间的力的传递和影响。

平面机构力分析的目的是确定各个部件之间的相对运动和受力情况，从而确定设计参数和优化设计。

首先，进行平面机构的力分析需要了解机构的运动副类型和特点。

平面机构包括直线副、转动副和滑动副等，而不同类型的运动副对应不同的受力情况。

例如，直线副的受力主要是拉力和压力，转动副的受力主要是转轴上的扭矩和轴承力，滑动副的受力主要是摩擦力和压力等。

其次，需要确定机构的约束和自由度，以及受力分析的基准点和坐标系。

约束是机构中连接各部件的运动约束，包括固定约束和运动约束；自由度是机构允许的运动自由度，通过自由度的分析可以了解机构的运动特性。

基准点和坐标系的选择是为了方便受力分析和结果的表示。

接下来，通过自由度分析和约束条件，可以得到机构中各个部件之间的受力关系。

根据受力分析的原理，可以采用静平衡条件、动力学方程或功率分析等方法来计算各个部件的受力情况。

静平衡条件可以用来计算处于平衡状态时的受力情况，动力学方程可以用来计算部件在运动过程中的受力情况，功率分析可以用来计算部件之间的能量传递和能量转换情况。

最后，通过力分析的结果可以进行力学设计和性能评估。

根据受力情况，可以确定各个部件的尺寸、材料和结构形式，以满足所要求的工作条件。

同时，还可以通过分析得到的各个部件的受力情况，来评估机构的运动稳定性和工作性能，从而进行优化设计和改进。

总的来说，机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。

通过力分析可以了解机构中各个部件之间的力的传递和影响，为机构的设计和优化提供基础。

力分析需要了解机构的运动副类型和特点，确定约束和自由度，选择基准点和坐标系，采用适当的方法进行受力分析，最后进行力学设计和性能评估。

机械原理之平面机构的力分析1. 引言在机械设计中，平面机构是一种常用的力传递装置。

它由多个固定的连杆构成，通过铰链连接点连接。

平面机构广泛应用于各种机械设备中，如发动机、传动装置等。

为了正确设计和优化平面机构，了解力的分析是很重要的。

本文将介绍平面机构的力分析方法，包括静力学方法和动力学方法。

2. 静力学方法静力学方法可以帮助我们计算平面机构的力。

它主要根据平衡条件和力的平衡方程来进行计算。

2.1 平衡条件平面机构的平衡条件是指在任何时刻，机构中的各个连杆受力之和为零。

这可以表示为以下公式：$$ \\sum F_x = 0 $$$$ \\sum F_y = 0 $$其中F x和F y分别表示平衡方程的水平和垂直分量。

2.2 力的平衡方程力的平衡方程可以通过使用力向量的加法和减法来得到。

在平面机构中，力的平衡方程可以表示为以下公式：$$ \\sum F_x = \\sum F_{xi} \\cos(\\theta_i) - \\sum F_{xj}\\cos(\\theta_j) = 0 $$$$ \\sum F_y = \\sum F_{yi} \\sin(\\theta_i) - \\sum F_{yj}\\sin(\\theta_j) = 0 $$其中F xi和F yi是作用在连杆上的水平和垂直分力，$\\theta_i$是作用力的夹角，$\\sum F_{xj}$和$\\sum F_{yj}$是作用在铰链上的水平和垂直反力，$\\theta_j$是反力的夹角。

2.3 举例说明假设我们有一个简单的平面机构，由两个连杆和一个铰链组成。

其中，连杆1的长度为l1，连杆2的长度为l2。

连杆1和连杆2之间的夹角为$\\theta$，铰链受到的水平反力和垂直反力分别为F xj和F yj。

现在我们需要计算连杆1和连杆2受力的大小和方向。

根据力的平衡方程，我们可以得到以下公式：$$ F_{x1} - F_{x2} \\cos(\\theta) = 0 $$$$ F_{y1} + F_{yj} - F_{y2} \\sin(\\theta) = 0 $$通过解这些方程，我们可以得到连杆1和连杆2受力的大小和方向。

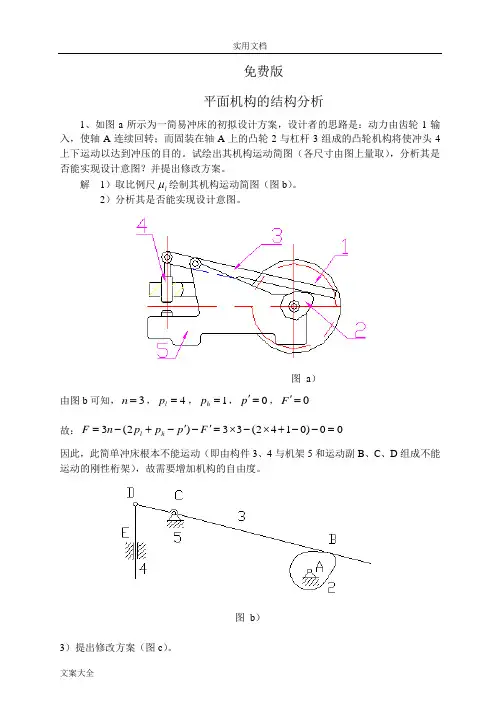
免费版 平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。

解 1）取比例尺l μ绘制其机构运动简图（图b ）。

2）分析其是否能实现设计意图。

图 a ） 由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F 故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。

图 b ）3）提出修改方案（图c ）。

为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。

图 c1） 图 c2）2、试画出图示平面机构的运动简图，并计算其自由度。

图a ）解：3=n ，4=l p ，0=h p ，123=--=h l p p n F图 b ）解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。

将其中的高副化为低副。

机构中的原动件用圆弧箭头表示。

3－1解3－1：7=n ，10=l p ，0=h p ，123=--=h l p p n F ，C 、E 复合铰链。

3－2解3－2：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度3－3 解3－3：9=n ，12=l p ，2=h p ，123=--=h l p p n F4、试计算图示精压机的自由度解：10=n ，15=l p ，0=h p 解：11=n ，17=l p ，0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=（其中E 、D 及H 均为复合铰链） （其中C 、F 、K 均为复合铰链）5、图示为一内燃机的机构简图，试计算其自由度，并分析组成此机构的基本杆组。

免费版平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。

解 1）取比例尺l μ绘制其机构运动简图（图b ）。

2）分析其是否能实现设计意图。

图 a ） 由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F 故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。

图 b ）3）提出修改方案（图c ）。

为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。

图 c1） 图 c2）2、试画出图示平面机构的运动简图，并计算其自由度。

图a ）解：3=n ，4=l p ，0=h p ，123=--=h l p p n F图 b ）解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。

将其中的高副化为低副。

机构中的原动件用圆弧箭头表示。

3－1解3－1：7=n ，10=l p ，0=h p ，123=--=h l p p n F ，C 、E 复合铰链。

3－2解3－2：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度3－3 解3－3：9=n ，12=l p ，2=h p ，123=--=h l p p n F4、试计算图示精压机的自由度解：10=n ，15=l p ，0=h p 解：11=n ，17=l p ，0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=（其中E 、D 及H 均为复合铰链） （其中C 、F 、K 均为复合铰链）5、图示为一内燃机的机构简图，试计算其自由度，并分析组成此机构的基本杆组。

机械原理 第八版 西北工业大学 平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。

解 1）取比例尺l μ绘制其机构运动简图（图b ）。

2）分析其是否能实现设计意图。

图 a ） 由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F 故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。

图b）3）提出修改方案（图c）。

为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。

图c1）图c2）2、试画出图示平面机构的运动简图，并计算其自由度。

图a ）解：3=n ，4=l p ，0=h p ，123=--=h l p p n F图 b ）解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。

将其中的高副化为低副。

机构中的原动件用圆弧箭头表示。

3－1解3－1：7=n ，10=l p ，0=h p ，123=--=h l p p n F ，C 、E 复合铰链。

3－2解3－2：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度3－3 解3－3：9=n ，12=l p ，2=h p ，123=--=h l p p n F4、试计算图示精压机的自由度解：10=n ，15=l p ，0=h p 解：11=n ，17=l p ，0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=（其中E 、D 及H 均为复合铰链） （其中C 、F 、K 均为复合铰链）5、图示为一内燃机的机构简图，试计算其自由度，并分析组成此机构的基本杆组。