下载文档原格式
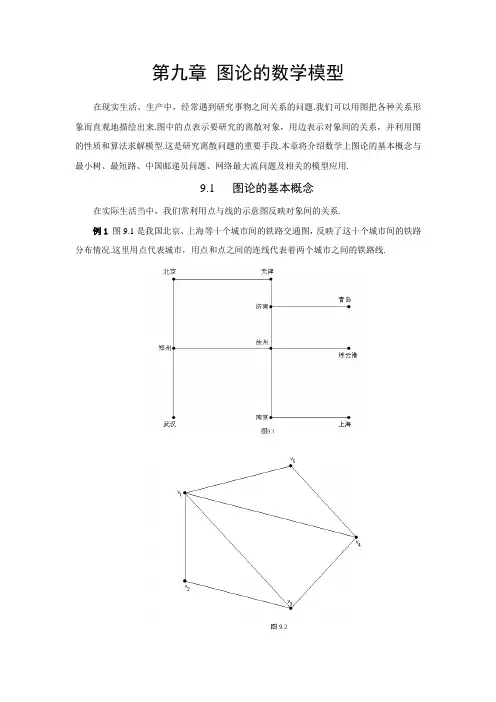
第九章图论的数学模型在现实生活、生产中，经常遇到研究事物之间关系的问题.我们可以用图把各种关系形象而直观地描绘出来.图中的点表示要研究的离散对象，用边表示对象间的关系，并利用图的性质和算法求解模型.这是研究离散问题的重要手段.本章将介绍数学上图论的基本概念与最小树、最短路、中国邮递员问题、网络最大流问题及相关的模型应用.9.1 图论的基本概念在实际生活当中，我们常利用点与线的示意图反映对象间的关系.例1图9.1是我国北京、上海等十个城市间的铁路交通图，反映了这十个城市间的铁路分布情况.这里用点代表城市，用点和点之间的连线代表着两个城市之间的铁路线.例2 有甲、乙、丙、丁、戊五个球队，它们之间比赛的情况，也可以用图表示出来.已知甲队和其它各队都比赛过一次，乙队和甲、丙队比赛过，丙队和乙、丁队比赛过，丁队和丙、戊队比赛过，戊队和甲、丁队比赛过.为了反映这个情况，可以用点v1,v2,v3,v4,v5分别代表五个队，两队之间比赛过，就在这两个队相应点之间连一条线，这条线不过其它点，如图9.2所示.如果我们要进一步反映比赛中的胜负关系，可以用一条带箭头的连线表示，如甲队胜了乙队，可以从v1引一条带箭头的连线到v2.如图9.3反映了五个球队比赛的胜负情况，可见v1三胜一负，v4三场球全负等等.综上所述，图论中的图是由一些点及一些点间的连线组成的.它不同于通常意义的几何图形，它用点表示事物，用点间有无连线表示事物之间的某种关系，以一种抽象的形式来表达确定的事物.由上例知，点间的连线有的不带箭头，有的带箭头.为了区别起见，前者称为边，后者称为弧.如一个图G是由点及边所构成的，则称之为无向图（也简称图），记为G=(V , E) .式中V，E分别是G的点集合和边集合.一条连接点v i,v j∈V的边记为[v i,v j](或[v j,v i]).如图9.4是一个无向图.V={ v1,v2,v3,v4}，E={e1,e2,e3,e4,e5,e6,e7},其中e1=[v1,v2](或[v2,v1]). e2 =[v1,v2] e3=[v2,v3] e4=[v3,v4] e5=[v1,v4] e6=[v1,v3] e7=[v4,v4] .如果一个图D式由点及弧所构成的，则称为有向图，记为D=(V,A).式中V,A分别表示D的点集合和弧集合.一条方向从v i指向v j的弧记为（v i,v j）.如图9.5是一个有向图.V={ v1,v2,v3,v4,v5}. A={a1,a2,a3,a4,a5,a6}.其中，a1=( v1,v2),a2=( v2, v1),a3=( v1, v3), a4=( v4 ,v2),a5=( v3, v4),a6=( v4, v5).下面再介绍一些常见名词和记号.考虑无向图G=(V , E).若边e=[u,v] ∈E,则称u,v是e的端点，也称u,v是相邻的.称e是点u（及点v）的关联边.若图G中，某个边的两个端点相同，则称e是环（如图9.7中的e7）.若两个点之间有多于一条的边，称这些边为多重边（如图9.4中的e1,e2）.一个无环、无多重边的图称为简单图.一个无环，但允许有多重边的图称为多重图.以点v 为端点的边的个数称为v 的次，记为d(v).如图9.4中d(v 1)=4,d(v 2)=3,d(v 4)=4(环e 7在计算d(v 4)作两次算).次为奇数的点，称为奇点，否则称为偶点.给定一个图G=(V , E).一个点、边交错序列（1i v ,1i e ,2i v ,2i e ,…,1-k i v ,1-k i e k i v ）,如果满足t i e =[t i v ，1+t i v ]（t=1,2,3, …k -1）.则称之为一条联结链1i v ，k i v 的链，记为（1i v ,2i v ,,…,1-k i v , k i v ）.链（1i v ,2i v ,,…,1-k i v , k i v ）中，若1i v =k i v ，则称之为一个圈，记为（1i v ,2i v ,…1-k i v , 1i v ）.若链中（1i v ,2i v ,,…k i v ）中，1i v ,2i v ,,…k i v 都是不同的，则称之为初等链；若圈中（1i v ,2i v ,…,1-k i v , 1i v ）中1i v ,2i v ,…,1-k i v 都是不同的，则称之为初等圈；若链（圈）中含的边均不相同，则称之为简单链（圈）.以后说到链（圈），除非特别交代，均指初等链（圈）.例如图9.6中，（v 1,v 2,v 3,v 4,v 5,v 3,v 6）是简单链，但不是初等链.（v 1,v 2,v 3,v 4,v 5）是一条初等链.（v 1,v 2,v 3,v 4,v 1）是初等圈.（v 4,v 1,v 2,v 3,v 5,v 7,v 6,v 3,v 4）是简单圈，但不是初等圈.图中不存在v 1到v 9的链.图G 中，若任何两点之间，至少有一条链，则称G 是连通图.否则称不连通的图.给定一个图G=(V , E).若)E ,V (G ''='使V=V '及E '⊆E ，称G '是G 的支撑子图.如图9.7中，（b ）是（a ）的支撑子图，而（c ）不是.设给有向图D=(V ,A) .从D 中去掉弧上的箭头，所得到的无向图称D 的基础图.D 中一条弧a=(u,v), u 称a 的始点，v 称a 的终点.称弧是从u 指向v 的.设（1i v ,1i a ,2i v ,2i a ,…1-k i v ,1-k i a ,k i v ）是D 中的点、弧交错序列，在基础图中对应一条链，称为D 的链.类似的定义D 中圈.如（1i v,1i a,2i v,2i a,…1-k i v,1-k i a,k i v）是D中一条链，且t i a=（t i v，1+t i v）称从1i v到k i v 的一条路.若路中的第一个点和最后一个点相同，称回路.如图9.8（v1,v3,v4,v5）是从v1到的v5路，（v1,v2,v4,v5）是链，不是路.（v1,v3,v4,v2,v1）是回路.注：对无向图、链与路（圈与回路）这两个概念是一致的.9.2最小支撑树与最短路9.2.1最小支撑树（最小生成树）及其算法.例1 已知有五个城镇，要再它们之间架电话线，要求任何两个城镇都可以互相通话.（允许通过其它城镇），并且电话线的根数最少.用五个点v1,v2,v3,v4,v5代表五个城镇.如果在某两个城镇之间架设电话线，则在相应两个点之间连一条边，这样一个电话线网就可以用一个图来表示.为了使任何两个城镇都可以通话，这样的图必须是连通的.其次，若图中有圈，从圈上任去一边，余下图任连通，省去一根电话线.因而，满足条件的电话线网对应的图必是连通、不含圈的图.如图9.9定义1. 一个无圈的连通图称树.定义2.设图T=(V, E')是G=(V , E)的支撑子图，如果图T=(V, E')是一个树，则称T 是G的支撑树.定义3. 图G=(V , E)，G中每一条边[v i,v j]，相应地有一个数w ij，则称这样的图G为赋权图. w ij称为边[v i,v j]的权.这里所说的“权”，是指与边有关的数量指标.根据实际问题的需要，可以赋予它不同的含义，例如表示距离、时间、费用等.赋权图不仅指出各点间的邻接关系，同时也表示出各点间的数量关系.定义4. 设有连通图G=(V , E)，对每一e=[v i,v j]有一非负权，w(e)= w ij.如果T=(V, E')是G的支撑树，称E'中所有边权数之和为支撑树T的权，记为w(T).即w(T)=∑w ij.[vi,∈Tvj]如果支撑树T*的权w(T*)是所有支撑树的权中最小者，则称T*是G的最小支撑树（简min w(T).称最小树）.既w(T*)=T最小支撑树有其广泛的应用，如例1，支撑树有多种，如给出各城镇间的道路长度，我们则应选用造价最低的电话线网.这个问题就是赋权图上的最小树问题.下边就是介绍求最小树的算法.方法一、（避圈法）该算法是1956年由Kruskal（克鲁斯凯尔）提出.步骤如下：设G为由m个节点构成的连通赋权图.(1)先把G中所有边按权数大小由小到大重新排列，并取权数最小的一条边取为T中的边.(2)从剩下的边中按（1）中排列取下一条边.若该边与前已取进T中的边形成某个回路，则舍去该边；否则把该边取进T中.重复步骤（2），直至有m-1条边取进T中为止，则这m-1条边就组成G的最小支撑树.例2 （如图9.10）8个城市v0,v1,…,v7之间有一个公路网，公路为图中的边，边上的权数表示公路的长度，现要沿公路架设电话线，要求如何架设，使电话线总长最小.解：这个问题就是求图9.10上的最小树.先按各边权数由小到大排列.为e1=[v0,v1], e2=[v2,v3], e3=[v1,v2], e4=[v0,v2]，e5=[v5,v6], e6=[v3,v4]，e7=[v1,v3]，e8=[v4,v5]，e9=[v4,v7]，e10=[v0,v5]，…顶点数m=8. 由Kruskal法的步骤，顺次试将e1,e2,e3,e4,e5,e6,e7,e8,e9取进T中（舍去e4和e7），于是最小支撑树T={ e1,e2,e3,e5,e6,e8,e9}.如图9.11.方法二、（破圈法）任取一圈，从圈中去掉一条权最大的边（如果有两条或两条以上的边都是权最大的边，则任意去掉其中一条）.在余下的图中，重复这个步骤，一直得到一个不含圈的图为止，这时的图便是最小树.用破圈法解上题，任取一圈，比如（v1,v0,v6,v1），边[v6,v0]最大，于是去掉；取圈（v1,v0,v2,v1），边[v0,v2]与[v1,v2]都为2，任去一边[v0,v2].如此下去，得到一个不含圈的图.即为最小树.9.2.2 最短路问题及Dijkstra(迪杰斯特拉)算法.一个典型的最短路问题如下：例3. 8个城市之间v0,v1,…,v7之间有一个公路网（如图9.12）.每条公路为图中的边，边上的权数表示通过该公路所需的时间.你在城市v0,从v0到v7应该选择什么路径，所需时间最少？即求d(v0,v7) (表示从v0到v7的最短路径的和)目前公认解决最短路的最佳算法是由Dijkstra提出的.这个算法不仅得到从v0到v7的最短路，还会得到由v0出发到其它各点的最短路.Dijkstra法的基本思想是从v0出发，逐步向外探寻最短路.执行过程中，与每个点对应，记寻下一个数（称为这个点的标号），它或者表示从v0到该点的最短路的权（称为P标号），或者是从v0到该点的最短路权的上界（称为T标号）.方法的每一步是去修改T标号，并且把T标号点改为具有P标号的点，从而使G中具P标号的顶点数多一个.这样，经过p－1步（p 是图中点的个数），就可求出从v 0到各点的最短路.在叙述Dijkstra 算法之前，以例3为例说明一下这个方法的思想.例3中，v 0出发，w ij ≥0.故有d(v 0 ,v 0)=0.这时v 0是具有P 标号的点.考察从v 0出发的三条边，[v 0,v 1], [v 0,v 2] ,[v 0,v 3].从v 0出发，沿[v 0,v 1]到达v 1,需时间d(v 0 ,v 1)+w 01=2；如从v 0出发，沿[v 0,v 2]到达v 2,需时间d(v 0 ,v 0)+w 02=8；类似的，沿[v 0,v 3]到v 3,需时间d(v 0 ,v 0)+w 03=1.因min{ d(v 0 ,v 0)+w 01, d(v 0 ,v 2)+w 02, d(v 0 ,v 0)+w 03}=1.可断言，从v 0出发到v 3的最短路需时间1.即d(v 0 ,v 3)=1.最短路（v 0,v 3）.这时因为从v 0到v 3的任一条路，如不是（v 0,v 3），则必先从v 0沿[v 0,v 1]到达v 1，或沿[v 0,v 2]到达v 2.但如此，此时已需时间2或8，不管再如何从v 1或v 2到达v 3,所需时间不会比1少.因而推知d(v 0 ,v 3)=1.这样使v 3具有P 标号.现在考察从v 0,v 3指向余点的边.由上已知，从v 0出发，沿[v 0,v 1]到达v 1,需时间为2；如从v 0出发，沿[v 0,v 2]到达v 2,需时间为8；从v 3出发，沿[v 3,v 2]到达v 2,需时间d(v 0 ,v 3)+w 32=8，从v 3出发，沿[v 3,v 6]到达v 6,需时间d(v 0 ,v 3)+w 36=10.因min{ d(v 0 ,v 0)+w 01, d(v 0 ,v 2)+w 02, d(v 0 ,v 3)+w 32, d(v 0 ,v 3)+w 36}= d(v 0 ,v 0)+w 01=2,基于同样的理由，从v 0到v 1的最短路是：（v 0 ,v 1），即d(v 0 ,v 1)=2.又使v 1变成具有P 标号的点.如此重复，直到求出v 0到v 7的最短路.下面给出Dijkstra 的一般步骤：用P ，T 表示某点的P 标号、T 标号，S i 表示第i 步时，具P 标号的点集.1. （i =0）令S 0={v s } 对于v ≠v s ,T(v)=+∞.2. 如果S i =V (V 表示图中所有点的集合),算法终止，这时考察对每个v ∈S i ,d(v s ,v)=P(v)；否则，进入3.3. 考察每个使[v k ,v j ]∈E 且v j ∉S i 的点.如果T(v j )＞P(v k )+w kj ,则把 T(v j )改为P(v k )+w kj ；否则，转入4.4. 令T(i j v )=ij S v ∉min {T(v j )}.把i j v 的T 标号变为P 标号，P(i j v )=T(i j v );令S i+1=S i +{i j v },转入2；现用该法求例3，v 0到 v 7的最短路.1． v s =v 0,S 0={v 0}.P(v 0)=0.2． [v 0,v 1]∈E, v 1∉S 0, P(v 0)+w 01＜T(v 1), T(v 1)修改为P(v 0)+w 01=2.同理 T(v 2)修改为P(v 0)+w 02=8; T(v 3)修改为P(v 0)+w 03=1.3． 在所有T 标号中，T(v 3)最小.于是令P(v 3)=1.S 1={v 0,v 3}.i =1.2. T(v 6)=P(v 3+w 36)=10.3. 在所有标号中，T(v1)=2最小，令P(v1)=2. S2={v0,v1,v3}.i=2.2. T(v4)=P(v1)+w14=3.3. 在所有标号中，T(v4)=3最小，令P(v4)=3.S3={ v0,v1,v3,v4}.i=3.2. T(v7)=12, T(v5)=6.3. 在所有标号中，T(v5)=6最小，令P(v5)=6.S4={ v0,v1,v3,v4,v5}.i=4.2. T(v2)=7.3. 在所有标号中，T(v2)=7最小，令P(v2)=7.S5={ v0,v1,v2,v3,v4,v5}.i=5.2. T(v6)=9.3. 在所有标号中，T(v6)=9最小，令P(v6)=9.S6={ v0,v1,v2,v3,v4,v5,v6}.i=6.2. T(v7)=12.3. 在所有标号中，T(v7)=12最小，令P(v7)=12.S7={ v0,v1,v2,v3,v4,v5,v6,v7}.i=7.因为S7=V，所以终止.从v0到v7的最短路d(v0,v7)=P(v7)=12.路径为（v0,v1,v4,v7）或（v0,v1,v4,v5,v7）或（v0,v1,v4,v2,v6,v7）.9.3中国邮递员问题一名邮递员带着要分发的邮件出发，经过要分发的每条街道，送完邮件后又返回邮局.如何设计送件路线，以尽可能少的行程来完成送邮件的任务.这类问题是由我国的管梅谷教授于1962年提出，国际上称为中国邮递员问题.若要把它抽象为图论的语言，就是在一个连通的赋权图中，寻找一个圈，过每边至少一次，使圈的总权最小.为了解决这个问题，我们先了解一下有关一笔画的问题.给定一个连通多重图G，若存在一条链，过每边一次，其仅一次，则称链为欧拉链.若存在一个简单圈，过每边一次，称欧拉圈.一个图有欧拉圈，则称为欧拉图.显然，一个图若能一笔画出，此图必是欧拉圈或含有欧拉链.定理1 连通多重图G是欧拉图当且仅当G中无奇点.（证略）有了以上知识，我们就可知，如果邮递员负责的范围，街道图如无奇点，就可从邮局出发，走每条街道一次，且仅一次，回到邮局.这样的路程最优.而对于有奇点的街道，就必须在某些街道重复一次或多次.如图9.13的街道图中，若v1是邮局，邮递员可按路线：v1→v2→v3→v4→v1→v6→v5→v4→v1(总权12)，也可按路线：v1→v2→v3→v4→v1→v6→v5→v4→v5→v6→v1(总权16).按第一条路线，在边[v1,v4]上重复一次.而第二条路线，在[v5,v4][v6,v5][v6,v1]重复一次.如果在某条路线中，边[v i,v j]重复几次，我们在图v i,v j之间增加几条边，每条边的权和原来的权相等.新增加的边称重复边.这条路线是相应新图的欧拉圈，如图9.14（a）和（b）.显然，两条路线的总路程差等于相应重边权的差.因而，原问题可以叙述为在一个有奇点的图中，增加重复边，使新图不含奇点，且重复边总权最小.我们把新图不含奇点而增加重复边的方案，称为可行方案.使总权最小的可行方案称为最优方案.方法分两步：一、可行方案的确定方法.因为在任一图中，奇点个数必为偶数.所以图中有奇点，就可以配成对.又因图连通，故每对奇点间必有一条链.我们把这条链的所有边作为重复边加到图中，可见新图必无奇点，成为可行方案.例1 图9.15中的街道图，有v2,v4,v6,v8四个奇点，我们以v2,v4为一对，v6,v8为一对.在图9.15中，连v2与v4的链中任一条，例取（v2,v1,v8,v7,v6,v5,v4）,并加上相应的重复边.同样任取v6与v8间的链（v8, v1,v2,v3,v4,v5,v6）,并加上相应的重复边，得图9.16.这个图，没有奇点.故已是欧拉图.总权为2w12+w23+w34+2w45+2w56+w67+w78+2w18=51二、调整可行方案，使重复边总长下降.（a）在最优方案中，图的每一条边最多有一条重复边.一般情况下，若[v i,v j]上有两条以上重复边，去掉偶数条.例如图9.16 [v1,v2]有两条重复边，都去掉，图仍无奇点.但总长度下降，仍是可行方案.对其它重复边也是如此.得图9.17.（b）在最优方案中，图中每个圈上重复边的权不大于该圈总权的一半.我们看到，如图中某圈重复边去掉，给原来没有的加上，图中仍无奇点.因而，如某圈重复边总权数大于该圈一半，用上面的方法调整，总权下降.例如图9.17中，圈（v2,v3,v4,v9,v2）总长24，重复边总权数14，大于总数的一半，作一次调整.以[v2,v9],[v4,v9]上的重复边代替[v2,v3],[v3,v4]上的，重复边总权下降至10.如图9.18三、判断最优方案标准从上分析知，（a）与（b）是最优方案必须满足的，反之可行方案满足了（a）、（b）,则一定最优以此为标准，对可行方案检查，若满足（a）、（b），则最优；若不满足，则相应调整，直至满足.检查图9.18，圈（v1,v2,v9,v6,v7,v8,v1）,重复边总权13，圈总权24，不满足.调整得图9.19.检查图9.19，（a）、（b）均满足，于是得最优方案.9.4网络最大流问题在实际问题当中，有许多关于网络流量得问题.如运输网络中的车量流、电路网络中的电流，通讯网络中的信息流，水管网络中的水流等等.先看一实例，如图9.20，是一个石油输送管网，顶点表示石油的转送站，各条弧表示石油输送的管道，以及石油的流动方向.由于历史原因，各管道的半径不同，即输送能力不同.问应该如何安排管道内的实际流量，使充分利用管网而达到最大流量.图9.20，要求通过石油管网，从v 1运送v 6至，弧边的数字代表了这条管道的最大运输能力.图9.21给出了一个方案，弧旁的数字代表实际每条管道的流量，这要求每条管道的流量不超过最大的流量，又要尽可能使总流量大，很明显这个方案还不是最优，那么应如何调整，最大输送量是多少？下面就来研究类似的问题，找到一个一般的解决方法.定义1. 给定一个有向图D=(V , A)在V 中指定一点，称发点，记v s .另一点称收点，记v t .其余称中间点.对于每条弧（v i ,v j ）∈A ，对应c ij ≥0称弧的容量.这样的D 叫作网络，记D=(V ,A,C).所谓网上的流，指弧（v i ,v j ）上的实际流量，记f ij .如例1图9.20中，v 1是发点，v 6是收点，其余是中间点.弧旁的数字是c ij .图9.21的运输方案，即是网上的一个流，每条弧上的实际通过量就是流量，即f 12=5，f 24=2，f 34=1等.在运输网络中，可以看到两个明显的要求：一是每个弧上的流量不超过弧的容量；二是中间点的流量为零.由于中间点只起转运作用，流入多少，流出多少.易见发点的净流出量与收点的净流入量相等，也是方案的总输送量.定义2 满足下述条件的流f 称可行流：1） 容量限制条件：对每个弧（v i ,v j ）∈A, 0≤f ij ≤c ij .2） 平衡条件：对于中间点，流出量=流入量.即对每个i (i ≠s , t )有∑∈A v v j i ),(f ij ﹣∑∈A v v i j ),(f ji =0对于发点，记∑∈A v v j s ),(f sj ﹣∑∈A v v s j ),(f js = v(f) 对于收点，记∑∈A v v i t ),(f ti ﹣∑∈A v v t i ),(f it = -v(f)式中v(f) 称为这可行流的流量，即发点的净输出量（或收点的净输入量）.可行流总是存在的.比如令所有弧的流量f ij =0,就是一个可行流（称零流）.其流量v(f)=0. 最大流问题就是求一个流{f ij }使其流量v(f)达到最大，并满足：0≤f ij ≤c ij （v i ,v j ）∈A (9.4.1)∑f ij +∑f ji =t i ts i s i f v f v =≠=⎪⎩⎪⎨⎧-,)()(0)( (9.4.2)我们可看到最大流问题是一个特殊的线性规划问题.即求一组{f ij },在满足(9.4.1)和(9.4.2)条件下，使v(f)最大.但我们将会利用图的特点，解决这个问题.先来认识一下增广链.给一个可行流f={f ij }.网络中f ij =c ij 的弧称饱和弧，使f ij ＜c ij 的弧称非饱和弧.把f ij =0的弧称为零流弧，f ij ＞0的弧称为非零流弧.如图9.21 中，（v 5,v 4）是饱和弧，其余为非饱和弧；所有弧是非零流弧.若μ是网络中连v s 到v t 的链，定义链的方向是v s 到v t ，则链上的弧分为两类：一类弧方向与链一致，称前向弧.全体前项弧记μ+；另一类与链方向相反，称后向弧. 全体前项弧记μ-.如图9.21中，链μ=（v 1,v 2,v 3,v 4,v 5,v 6）中. μ+={(v 1,v 2), (v 2,v 3), (v 3,v 4), (v 5,v 6)}; μ- ={(v 5,v 4)}.定义3 设f 是可行流，μ是v s 到v t 的一条链，若μ满足下列条件，称为增广链： 在弧（v i ,v j ）∈μ+上，0≤f ij ＜c ij ，即μ+中每一弧是非饱和弧.在弧（v i ,v j ）∈μ-上，0＜f ij ≤c ij ，即μ-中每一弧是非零流弧.图9.21中，链μ=（v 1,v 2,v 3,v 4,v 5,v 6）就是增广链.设S,T ⊂V, S∩T=Ø，我们把始点在S ，终点在T 的所有弧构成的集合，记为（S,T ）. 定义4 网络D=(V ,A,C)，若点集V 被剖分为两个非空集合V 1和1V ，使v s ∈V 1, v t ∈1V ,则把弧集（V 1, 1V ）称为是截集.显然，若把某一截集（V 1, 1V ）的弧从网络中丢去，则从v s 到v t 不存在路.所以，直观上讲截集是从v s 到v t 的必经之道.定义5 给一截集（V 1, 1V ），把截集中所有弧容量之和称为这个截集的容量（简称为截量）.记为c(V 1, 1V ) 即c(V 1, 1V )=∑∈),(),(ij 11c V V v v j i不难证明，任何一个可行流的流量v(f)都不会超过任一截集的容量.即v(f) ≤c(V 1, 1V ). 显然，若对于一可行流f *，网络中的截集（V 1*, 1V *），使f *=c(V 1*, 1V *),则f *是最大流，而(V 1*, 1V *)必定是D 的所有截集中，容量最小的一个，即最小截集.因此任一网络D 中，从v s 到v t 的最大流量等于最小截集的容量.我们可以利用增广链来求得这个最大流.这个方法的思想是：先给定一个可行流f ，在D 中寻找增广链，在这条链上改变流量，得到流量增大的新的可行流.如再找不到增广链，则已达到最大流.实际计算中，我们采用最大流标号法（Ford, Fulkerson ）从一个可行流出发（若网络中无可行流f ，则可用零流），经过标号过程和调整过程.1） 标号过程.在这个过程中，网络中的点或者是标号点（又分为已检查和未检查两种），或者是未标号点.每个标号点的标号分两部分：第一标号表明它的标号从哪一点得到的，以便找增广链；第二个标号，是为确定增广链的调整量θ.标号过程开始，总先给v s 标上（0，+∞），这时v s 是标号而未检查的点，其余都是未标号点.一般地，取一个标号而未检查的点v i ，对一切未标号点v j ：(1) 若在弧（v i ,v j ）上，f ij ＜c ij ，则给v j 标号（v i , l(v j )）.这里l(v j )=min {l(v i ), c ij -f ij }.这时点v j 成为标号未检查点.(2) 若在弧（v j ,v i ）上，f ji ＞0，则给v j 标号（-v i , l(v j )）.这里l(v j )=min {l(v i ), f ji }.这时点v j 成为标号未检查点.于是v i 成为标号而已检查的点.重复上述步骤，一旦v t 被标上号，表明得到一条从v s 到v t 的增广链μ，转入调整过程.若所有标号都已经查过，而标号过程进行不下去，算法结束，可行流已是最大流.2） 调整过程.首先按v t 及其它点的第一个标号，利用“反向追踪”的办法，找出增广链μ.例如设v t 的第一个标号为v k (或-v k )，则弧(v k ,v t )(或(v t ,v k ))是μ上的弧.接下来检查v k 的第一个标号，若为v i (或-v i )，则弧(v i ,v k )(或(v k ,v i ))是μ上的弧.再检查v i 的第一个标号，依次下去，直到v s为止.这时被找出的弧就构成了增广链μ.令调整量θ是l(v t ),即v t 的第二个标号.令⎪⎩⎪⎨⎧∉∈∈+='+μ),(μ),(μ),(f -f f f -ij ij ij ij j i j i j i v v v v v v θθ 去掉所有的标号，对新的可行流f '={ij f '}.重新进入标号过程.例1. 用标号法求图9.22所示网络的最大流.弧旁的数是（c ij ,f ij ）.解：（一）标号过程.（1） 首先给v s 标上（0，+∞）.（2） 检查v s ,在弧（v s ,v 2）上，f s2=c s2=3不满足标号条件.弧（v s ,v 1）上，f s1＜c s1=5.则v 1的标号为（v s , l(v 1)）其中l(v 1)=min {l(v s ), c s1-f s1}=min{+∞,5-1}=4.（3） 检查v 1，在弧（v 1,v 3）上，f 13=c 13=2不满足标号条件. 在弧（v 2,v 1）上，f 21=1＞0.则v 2的标号为（-v 1, l(v 2)）其中l(v 2)=min {l(v 1),f 21}=min{4, 1}=1.（4） 检查v 2, 弧（v 2,v 4）上，f 24＜c 24.则v 4的标号为（v 2, l(v 4)）其中l(v 4)=min {l(v 2),c 24-f 24}=min{1,4-3}=1. 在弧（v 3,v 2）上，f 32=1＞0.则v 3的标号为（-v 2, l(v 3)）其中l(v 3)=min {l(v 2),f 32}=1.（5） 在v 3,v 4中任选一个进行检查.例如，弧（v 3,v t ）上，f 3t ＜c 3t .则v t 的标号为（v 3,l(v t )）其中l(v t )=min {l(v 3), c 3t -f 3t }=1.因v t 有了标号，故转入调整过程.（二）调整过程.按点的第一个标号找到一条增广链，如图9.23中粗线所示.易见μ+={(v s,v1), (v3,v t)}, μ-={(v2,v1),(v3,v2)}.按θ=1在μ上调整f.μ+：f s1+θ=1+1=2. f3t+θ=1+1=2.μ-：f21-θ=1-1=0. f3t-θ=1-1=0.其余f ij不变.调整后得如图9.24所示可行流，对这个可行流进入标号过程，寻找增广链.开始给v s标上（0，+∞）.于是检查v s,给v1标以（v s,3）.检查v1,弧（v1,v3）上，f13=c13;弧（v2,v1）,f21=0均不符合条件.标号过程无法进行下去，算法结束.这是可行流（图9.24）即为所求最大流.最大流量为v(f)=f s1+f s2=f 4t +f 3t =5.与此同时可找到最小截集（V 1, 1V ），其中V 1为标号点的集合, 1V 为未标号点集合.弧集合（V 1, 1V ），即为最小截集.上例中，V 1={v s ,v 1}, 1V ={v 2,v 3,v 4,v t }.于是（V 1, 1V ）={（v s ,v 2），（v 1,v 3）}是最小截集，它的容量必也是5.由上述可见，用标号法找增广链以求最大流的结果，同时得到一个最小截集.最小截集的容量的大小影响总流量的提高.因此要提高流量，必须先考虑改善最小截集中各弧的容量，提高它们的通过能力.另一方面，最小截集中的弧的通过能力被降低，就会使总的输送量减少.阅读材料哥尼斯堡七桥问题这是历史上一个有名的数学难题.此问题在1736年被Euler 解决之前一直使这个普鲁士城镇中的居民很感兴趣.18世纪，普鲁士的哥尼斯堡镇的普雷格尔河上有七座桥，这七座桥将河的两岸与河中的两个岛屿连接起来，如图9.25所示.假设两块岛屿用A 和B 表示，a,b,c,d,e,f,g 表示七座桥（图9.25）.问题：（1）一个人能否经过每座桥恰好一次？（2）能否恰好经过每座桥一次并且最后能回到原出发点？欧拉解决七桥问题采用了“数学模型”法.建模：既然岛屿与陆地无非是桥梁的连接地点，那么就不妨把4处地点缩小（抽象）成4个点，并把7座桥表示（抽象）成7条边，便得到了七桥问题的模拟图（图9.26），这样当然并没有改变问题的实质，于是人们企图一次无重复地走过7座桥的问题等价于一笔画出上述图形的问题（每条边必须且经过一次），此外，图9.26就是七桥问题的数学模型.Euler 解决七桥问题是先考虑一般化问题：如果给定任意一个河道图与任意多座桥，可否判断每座桥能否恰好走过一次呢？一般化的问题就是要有一个一般化的解法，才有更实际的意义，考察一笔画的结构特征，有个起点和终点（若起点和终点重合时即为Euler 图）.除起点与终点处，一笔画中出现的交点处总是一进一出的，故交点的度数（相连的边的数目和）为偶数，由此Euler给出了一般结论：1）连接奇数个桥的陆地仅有一个或超过两个以上，不能实现一笔画.2）连接奇数个桥的陆地仅有两个时，则从两者任意一块陆地出发，可以实现一笔画而停在另一陆地.3）每个陆地都连接有偶数个桥时，则从任意陆地出发，都能实现一笔画而回到出发点.对于模拟图，显然图必须是连通的，当且仅当图为欧拉图时，问题（2）才能实现.由图9.26知，问题无解.著名的七桥问题彻底解决了，进一步可知，对于任意一个河道图和任意多座桥的问题都解决了.评注一：从这个问题可以看出，欧拉不拘泥于特殊问题，而是要解决一般问题，这样才更具有科学价值，更能推动科学的发展；它并非去如何走一遍，而是去寻求一种一般的可能的判定法则，这是一种科学的思维方式；他将七桥难题化为一个图论问题（仅仅用点和边来描述），这种高度的抽象把问题表述的非常突出和清晰，并加以解决，后来人们公认他为图论的创始人.评注二：我对七桥问题的答案并不关心，但解决此问题时所表现出的智慧却几次让我惊讶不已.问题解决了，但比我们原先所期望得到的要多得多.把问题中所涉及的主要对象抽象成两类元素，点和直线，问题中所包含的结构关系便被清晰而简练地表达出来了.这是何等的深刻！四色问题问题：对任何一张地图进行着色，是任意两个有公共边界的国家染不同的颜色，那么最多有四种颜色就足够了.历史回顾：这叫地图的四色猜想，是一个著名的数学难题.这是在1852年，一位大学毕业生佛南西斯·哥里斯首先发现的，他把这个发现首先告诉了英国著名数学家德·摩根.德·摩根感到这是个有趣的数学问题，便用数学方法去证明，但没有证明出来.于是他又写信告诉了英国数学家汉米尔顿，汉米尔顿经过长达十三年的努力，直到离开人世也没有证明出来.1878年英国数学家凯莱在伦敦的数学年会上，饶有兴趣的提出了著名的四色猜想.其后经过一百多年的时间，许多数学家去证明，结果都没有成功.直到1976年9月，《美国数学会通告》宣布：美国伊利诺斯大学的两位教授阿普尔（K.Apple）和哈根（W.Haken），他们利用大型电子计算机，分析了两千多种复杂的地图（这些图，有些是实际存在的，有些是数学家为了证明四色猜想而构造出来的），包括几百万种情况，作了两百亿次逻辑判断，经过一千二百个机时的计算，证明了地图四色猜想是正确的.这一困扰着许多数学家一百多年的数学难题终于解决了.在证明四色猜想的过程中，获得了图论的许多重要结果，丰富了一些数学理论和方法.当然目前人们对这种繁琐的证明方法并不满意，力求寻找更简洁的方法.。
