2010年青岛科技大学数学分析考研试题

（1）青岛科技⼤学⾼数试卷10-11⾼数A2A卷2010/20112 ⾼等数学A2（ A 卷）数理学院机电，信息，应物等专业（答案写在答题纸上，写在试题纸上⽆效）⼀、填空题（每⼩题3分，共15分）1．设arctany z x =，则zx= 。

2．⼀阶线性微分⽅程23x dyy e dx+=的通解为。

3．设L 是椭圆周221x y +=，则曲线积分2(21) Lx x ds ++? 。

4．函数()sin f x x x =展开为x 的幂级数是。

5．已知向量(2,1,1),(1,1,3)a b ==-，则a b ?= 。

⼆、选择题（每⼩题3分，共15分）1．函数(,)f x y =0，0）处（）。

()A 偏导数存在 ()B 连续但偏导数不存在 ()C 可微 ()D 连续且偏导数存在2．⼆重积分31(,)xxdx f x y dy ?交换积分次序可化是（）。

()A 1(,)y dy f x y dx ? ()B 10(,)ydy f x y dx ?()C 10(,)ydy f x y dx ? ()D 1(,)ydy f x y dx ?3．曲⾯21z x y =+在点（1,1,2）处的切平⾯⽅程是（）。

()A 210x y z +--= ()B 210x y z +--= ()C 10x y z +--= ()D 10x y z ++-= 4．若级数1nn a∞=∑收敛，则级数20()nn n aa ∞+=+∑（）。

()A 绝对收敛 ()B 发散 ()C 收敛 ()D 敛散性不能确定5．以4为周期的函数在[2,2)-上的表达式为24,20()2,02x x f x x x +-≤的和函数为(),s x 则(2)s =（）。

课程考试试题学期学年拟题学院（系）: 适⽤专业:()A 1 ()B 2 ()C 0 ()D 3.三、（共21分）1、（7分）设(2,2)z f x y x y =-+，其中f 具有⼆阶连续偏导数，求2,z zx x y。

2009/20102 高等数学A （下）（ B 卷）数理学院 陈宁机自、测控、热能、应物等专业 彭翠英（答案写在答题纸上，写在试题纸上无效）一、填空题（每小题3分，共15分）1．已知向量)4,1,3(=a ，向量)2,0,1(-=b ，则=⋅b a . 2．设xy z =，则=)1,1(dz . 3．设积分曲线L 为422=+y x ，则曲线积分=⎰Lds 2 .4． 已知bxdy aydx +为某一函数),(y x f 的全微分，则a 与b 的关系是 . 5. 交换积分次序=⎰⎰22),(xdy y x f dx .二、选择题（每小题3分，共15分）1．方程组⎩⎨⎧==+14222z y x 在空间表示（ ）()A 圆 ()B 椭圆 ()C 椭圆柱面 ()D 两条直线2．设)(x f 为周期为π2的函数，它在区间](ππ，-上定义为⎩⎨⎧≤<≤<-=ππx x x x x f 0,20,)(，则)(x f 的傅立叶级数在π2=x 处收敛于 . ()A 0 ()B π2 ()C π3 ()D π43．极限220limyx xyy x +→→ . （A ） =0 (B) 21= (C) 不存在 (D) 以上都不对 4．将⎰⎰Ddxdy y x f ),(化为极坐标系下的二次积分为 ，其中D 为直线1,3,===x x y x y 所围成的三角形区域.(A)⎰⎰θππθθθsin 1034)sin ,cos (rdr r r f d （B ）⎰⎰θππθθθsin 1034)sin ,cos (dr r r f d课程考试试题学期学年拟题人:校对人: 拟题学院（系）: 适 用 专 业:（C ）⎰⎰θππθθθcos 1034)sin ,cos (dr r r f d （D ）⎰⎰θππθθθcos 1034)sin ,cos (rdr r r f d5．级数 ∑∞=-111n nn）（（ ）. ()A 发散 ()B 条件收敛 ()C 绝对收敛 ()D 以上均不是三、（共21分）1、（7分）设)ln(22y x z +=，求yx zy z x z ∂∂∂∂∂∂∂2,,. 2、（7分）计算二重积分dxdy y x ⎰⎰D，其中D 是由2y x =与y x =所围成的闭区域。

2010年全国硕士研究生入学统一考试数学一试题一、选择题：1~8小题，每小题4分，共32分，下列每题给出的四个选项中，只有一个选项符合题目要求，请将所选项前的字母填在答题纸．．．指定位置上. (1)极限2lim ( )()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦(A)1 (B)e(C)a be-(D)b ae-答案：C 详解：2lim ()()xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦=2233221ln ()()()()lim lim lim xxx x bx abxx x x a x b a bx a x b x ax bx abx x x e e ee⎛⎫-+-- ⎪⋅ ⎪-+--+⎝⎭-+-→∞→∞→∞===(2)设函数(),z z x y =，由方程(,)0y zF x x=确定，其中F 为可微函数，且20F '=，则x z x y u y ∂∂+∂∂=( ) (A)x (B)z (C)x - (D)z -答案：B详解：12221222,1x z y z y zF F F F F z x x x x x F F F x⎛⎫⎛⎫''-+-''⋅+⋅⎪ ⎪'∂⎝⎭⎝⎭=-=-=''∂'⋅112211y x F F F z x xF F F x'⋅''∂=-=-=-''∂'⋅1212222yF zF yF F z z z xyz xxF F F ''''+⋅∂∂+=-=='''∂∂(3)设,m n是正整数，则反常积分0⎰的收敛性(A)仅与m 的取值有关 (B)仅与n 取值有关 (C)与,m n 取值都有关 (D)与,m n 取值都无关 答案：C 详解：11222111111111ln 1(ln (1))1111mmn mm np p p nnx p p m dx p x p np -∞∞∞⋅⋅⋅⎛⎫⎛⎫⎛⎫- ⎪⎪ ⎪-⎛⎫⎝⎭⎝⎭⎝⎭==-= ⎪⎛⎫⎝⎭⎛⎫ ⎪ ⎪⎝⎭⎝⎭∑∑∑⎰⎰2121121n mm np n m m nn m p m n -∞--⎧>⎪⎛⎫⎪=⎨⎪-⎝⎭⎪≤⎪⎩∑收敛，发散， (4)()()2211limnnx i j nn i n j→∞--=++∑∑(A)()()12111x dx dy x y++⎰⎰(B)()()10111x dx dy x y ++⎰⎰(C)()()1100111dx dy x y ++⎰⎰(D)()()112111dx dy x y++⎰⎰答案：D详解：()()22211112limlim11nnnnx x i j i j nnn i nji j n n n n →∞→∞----=⎛⎫++⎛⎫⎛⎫+⋅⋅+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑∑2211111lim11n nx i j inj n n →∞--=⋅⋅⎛⎫++ ⎪⎝⎭∑∑()()112111dx dy x y=++⎰⎰(5)设A 为m n ⨯型矩阵，B 为n m ⨯型矩阵，E 为m 阶单位矩阵，若AB =E ，则( ) (A)秩(),r A m =秩()r B m =(B)秩(),r A m =秩()r B n = (C)秩(),r A n =秩()r B m = (D)秩(),r A n =秩()r B n =答案：A解析：由于A B E =，故()()r A B r E m ==，又由于()(),()()r A B r A r A B r B ≤≤，故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵，B 为n m ⨯矩阵，故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==，故选A 。

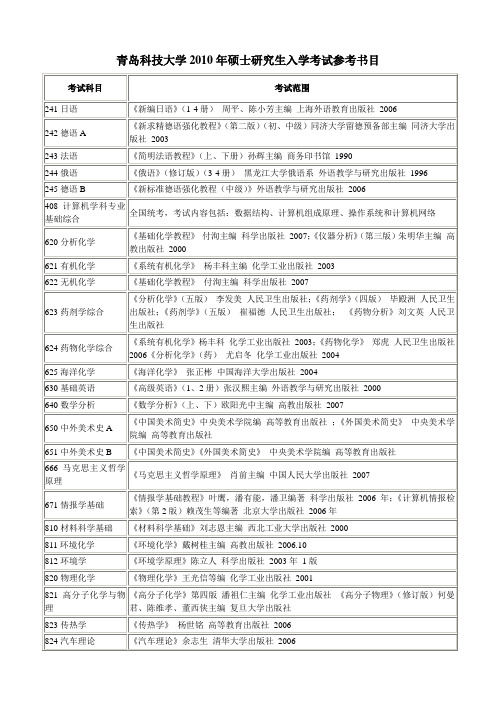
青岛科技大学2010年硕士研究生入学考试参考书目考试科目考试范围241日语《新编日语》（1-4册）周平、陈小芳主编上海外语教育出版社2006242德语A 《新求精德语强化教程》（第二版）（初、中级）同济大学留德预备部主编同济大学出版社2003243法语《简明法语教程》（上、下册）孙辉主编商务印书馆1990244俄语《俄语》（修订版）（3-4册）黑龙江大学俄语系外语教学与研究出版社1996 245德语B《新标准德语强化教程（中级）》外语教学与研究出版社2006408计算机学科专业基础综合全国统考，考试内容包括：数据结构、计算机组成原理、操作系统和计算机网络620分析化学《基础化学教程》付洵主编科学出版社2007；《仪器分析》（第三版）朱明华主编高教出版社2000621有机化学《系统有机化学》杨丰科主编化学工业出版社2003 622无机化学《基础化学教程》付洵主编科学出版社2007623药剂学综合《分析化学》（五版）李发美人民卫生出版社；《药剂学》（四版）毕殿洲人民卫生出版社；《药剂学》（五版）崔福德人民卫生出版社；《药物分析》刘文英人民卫生出版社624药物化学综合《系统有机化学》杨丰科化学工业出版社2003；《药物化学》郑虎人民卫生出版社2006《分析化学》（药）尤启冬化学工业出版社2004625海洋化学《海洋化学》张正彬中国海洋大学出版社2004630基础英语《高级英语》（1、2册）张汉熙主编外语教学与研究出版社2000 640数学分析《数学分析》（上、下）欧阳光中主编高教出版社2007650中外美术史A 《中国美术简史》中央美术学院编高等教育出版社；《外国美术简史》中央美术学院编高等教育出版社651中外美术史B《中国美术简史》《外国美术简史》中央美术学院编高等教育出版社666马克思主义哲学原理《马克思主义哲学原理》肖前主编中国人民大学出版社2007671情报学基础《情报学基础教程》叶鹰，潘有能，潘卫编著科学出版社2006年；《计算机情报检索》（第2版）赖茂生等编著北京大学出版社2006年810材料科学基础《材料科学基础》刘志恩主编西北工业大学出版社2000 811环境化学《环境化学》戴树桂主编高教出版社2006.10812环境学《环境学原理》陈立人科学出版社2003年1版820物理化学《物理化学》王光信等编化学工业出版社2001821高分子化学与物理《高分子化学》第四版潘祖仁主编化学工业出版社《高分子物理》（修订版）何曼君、陈维孝、董西侠主编复旦大学出版社823传热学《传热学》杨世铭高等教育出版社2006 824汽车理论《汽车理论》余志生清华大学出版社2006825材料力学《材料力学》刘鸿文主编高教出版社2004826机械设计《机械设计》濮良贵主编高教出版社2007827金属学与热处理《金属学与热处理》崔忠圻主编机械工业出版社2007828工程热力学《工程热力学》沈维道高教出版社2005；《工程热力学》陈贵堂编北京理工大学出版社2008；《工程热力学》华自强编高教出版社2001829工程力学《工程力学》《理论力学》王永岩主编科学出版社2007831控制原理《自动控制原理》（第四版）胡寿松科学出版社832电路《电路》（第五版）邱关源编高等教育出版社835化工原理《化工原理》夏青等主编天津大学出版社2005836生物化学《生物化学教程》（第三版）张洪渊主编四川大学出版社2003 837发酵工艺学《发酵工艺原理》熊宗贵主编中国医药科技出版社2005838生物催化与生物转化《生物催化的手性合成》张玉彬主编化学工业出版社2002839植物纤维化学《植物纤维化学》（第三版）杨淑蕙主编中国轻工业出版社2001 840管理学原理《管理学——原理与方法》周三多主编复旦大学出版社2006 841西方经济学《西方经济学》高鸿业主编中国人民大学出版社2007850综合考试《语言学教程》（修订版）胡壮麟主编北京大学出版社2001 《新编英汉翻译教程》孙致礼主编上海教育出版社2003860高等代数《高等代数》王萼方、石声明高教出版社2003870水污染控制工程《水污染控制工程》（下册）高延耀高等教育出版社2007871大气污染控制工程《大气污染控制工程》（第二版）郝吉明高等教育出版社2002 872安全系统工程《安全系统工程》汪元辉编天津大学出版社2006.10873化工单元运行安全技术《化工单元运行安全技术》崔克清化学工业出版社2006.3876美术理论《中国美学史》王振复复旦大学出版社2004.3；《西方美学史》朱光潜人民文学出版社1975.5；《美术概论》王宏建、袁宝林主编高等教育出版社880思想政治教育学原理《思想政治教育学原理》陈万柏，张耀灿高等教育出版社2007911微机原理与接口技术《微型计算机原理及应用》（第三版）郑学坚，周斌编著清华大学出版社。

2009/20102 概率论与数理统计（A 卷 ）数理学院 张菊芳全校 程尊水（答案写在答题纸上，写在试题纸上无效）一、填空题（每个小题3分，共15分） 1．nm n+； 2．0.2； 3. -1/2；4. 1；5. 1. 二、选择题（每个小题3分，共15分） 1． A ； 2. A ；3．D ；4. B ；5. C ．三、计算下列各题（每小题10分，共20分）1．解 设A =“取出的枪是校准过的”，B =“中靶”，则21(),(),(|)0.8,(|)0.333P A P A P B A P B A ====…………………………..2分（1）由全概率公式，有()()(|)()(|)P B P A P B A P A P B A =+……………..4分21190.80.33330=⨯+⨯=……………………...6分 （2）由贝叶斯公式，有()(|)(|)()P A P B A P A B P B =…………………………..8分20.8163191930⨯==…………………….......10分2．解 （1）X 的分布律为X 0 1 2 3 p k1/21/41/81/8…………..4分 (2)11117()012324888E X =⨯+⨯+⨯+⨯= ……………………………….…6分 22222111115()012324888E X =⨯+⨯+⨯+⨯=…………………………….….8分2271()()[()]64Var X E X E X =-=………………………………………..….10分四、计算下列各题（共28分） 1．（12分）解 （1）()1,f x dx ∞-∞=⎰即30sin 31A xdx π=⎰..…………….1分302cos3|133A A x π-==，32A =………………………………………….....3分 课程考试试题 学期 学年 拟题人:校对人: 拟题学院（系）: 适 用 专 业:（2）446631{}sin 3cos3|64224P X xdx x ππππππ<<==-=⎰…………………..5分 （3）()()xF x f t dt -∞=⎰……………………………………………………....6分00,03sin 3,0231,3xx tdt x x ππ⎧⎪≤⎪⎪=<≤⎨⎪⎪>⎪⎩⎰…………………………………………...9分0,01(1cos3),0231,3x x x x ππ⎧⎪≤⎪⎪=-<≤⎨⎪⎪>⎪⎩…………………………………………...12分2．（6分）解21,(0,1),20,12,()()y x x y x y x h y h y ''=+∈=><<===3分23()|()|,12()0,Y h y h y y f y '⎧⋅<<=⎨⎩其他…………………………………………….…5分2()0,Y y f y <<=⎪⎩其他 ………………………………….…6分3．(10分)解 ()(,)X f x f x y dy ∞-∞=⎰…………………………………….……1分226,016(),010,0,xx dx x x x x ⎧⎧<<-<<⎪==⎨⎨⎩⎪⎩⎰其他其他…………………4分 ()(,)Y f y f x y dx ∞-∞=⎰…………………………………..…….…5分,01),010,0,y dx y y y ⎧⎧<<<<⎪⎪==⎨⎨⎪⎪⎩⎩其他其他………………8分由于(,)()()X Y f x y f x f y ≠，所以X 与Y 不独立………………………………10分 五、计算下列各题（共17分） 1．（6分）解由于~(0,1)0.5X N μ-………………………………………1分||0.1{||0.1}{}0.050.50.5X P X P μμ--≥=≥≤……………………………2分2[1)]0.055-Φ≤ 即(0.975(1.96)5Φ≥=Φ…………………………………………4分1.96≥,解得96.04n ≥，所以n 至少取97…………………………5分2.（11分）（1）矩估计量11()E X x dx ==⎰…………2分X =，解得 2ˆ1X X θ⎛⎫= ⎪-⎝⎭…………………………………..5分（2）极大似然估计 当01i x ≤≤时，11()ni L θ==121nni xθ==∏……………………7分1ln ()ln 1)ln 2ni i nL x θθ==+∑11ln ()ln 02nii d n L xd θθθ==+=…………………………………..9分解得 221ˆln ni i n x θ==⎛⎫⎪⎝⎭∑所以极大似然估计量为221ˆln ni i n X θ==⎛⎫⎪⎝⎭∑………………………………11分六、证明题（5分）证明 因为~(0,2)i X N ,所以 12~(0,2)X X N +，~(0,1)U N =…………………………1分 22223453~V X X X χ=++，且U 与V 独立…………… 3分~(3)t =即~(3)Y t =………………………………5分。

2010年全国硕士研究生入学统一考试数学二试题一、选择题：1~8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内。

(1)函数()f x = (A) 0. (B) 1 (C) 2 (D) 3(2) 设1y ,2y 是一阶线性非齐次微分方程()()y p x y q x '+=的两个特解. 若常数λ, μ使12y y λμ+是该方程的解,12y y λμ-是对应的齐次方程的解, 则 （A ）11,22λμ== (B)11,22λμ=-=- (C) 21,33λμ== (D) 22,33λμ== (3) 曲线2y x =与曲线ln (0)y a x a =≠相切，则a =(A)4e (B)3e (C)2e (D)e(4)设,m n 为正整数,则反常积分dx ⎰的收敛性(A)仅与m 取值有关 (B)仅与n 取值有关(C)与,m n 取值都有关(D)与,m n 取值都无关(5)设函数(,)z z x y =由方程(,)0y z F x x=确定,其中F 为可微函数,且20F '≠则z z xy x y∂∂+=∂∂ (A) x(B)z (C) x -(D) z -(6) 2211lim()()nnn i j nn i n j →∞===++∑∑ (A)121(1)(1)xdx dy x y ++⎰⎰(B)11(1)(1)xdx dy x y ++⎰⎰(C) 11001(1)(1)dx dy x y ++⎰⎰ (D)112001(1)(1)dx dy x y ++⎰⎰（7）设向量组12 :, ,, r I ααα⋅⋅⋅可由向量组12II : , ,, s βββ⋅⋅⋅线性表示, 则列命题正确的是(A) 若向量组I 线性无关, 则r s ≤ (B) 若向量组I 线性相关, 则r s >(C) 若向量组II 线性无关, 则r s ≤ (D) 若向量组II 线性相关, 则r s >(8)设A 为4阶对称矩阵,且20A A +=若A 的秩为3,则A 相似于(A)1110⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(B)1110⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦(C) 1110⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦(D) 1110-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦ 二、填空题：9-14 小题，每小题 4分，共 24 分，请将答案写在答题纸指定位置上。

数学分析总复习题青岛科技大学数理系信息与计算科学专业第一章 函数思考题：1．何谓函数，函数关系，函数值？2．函数y=f(x)与方程y=f(x)在概念上有何区别？ 3．怎样确定函数的定义域？4．怎样才算完全确定了一个函数？应该如何规定两个函数相等？下面各对函数是否相等？(1)f(x)=x ，)2； (2)f(x)=x -1，g(x)=2x 1x 1-+；(3)f(x)= | x | ，；(5)f(x)=2x 1,x 11,x 1-≥⎧⎨<⎩，x ；(6)1,x 1f (x)x,1x 11,x 1-<-⎧⎪=-≤≤⎨⎪>⎩，{1g(x)|1x ||1x |}2=+--.5．若函数y=f(x)的反函数就是它本身，试问此函数的图象有什么样的特点？ 6．下列函数是否是初等函数？说明理由.(1)f(x)= | x | ； (2)xcosx f (x)(x sin x)=+；(3)f(x)=x 00,x 0>≤⎝， (4)f(x)=c,x cx,c x c c,x c-<-⎧⎪-≤≤⎨⎪>⎩. 7．设f(u)与u=(x)ϕ能复合为f((x)ϕ)，(1)若f(u)递增(递减)，(x)ϕ递减，试研究f((x)ϕ)的单调性.(2)若f(u)为奇(偶)函数，(x)ϕ为偶(奇)函数，试研究f((x)ϕ)的奇偶性.(3)若f(u)为任意函数，(x)ϕ为偶函数，试研究f((x)ϕ)的奇偶性.(4)若f(u)为有界函数，(x)ϕ为任意函数，试问f((x)ϕ)是否一定是有界函数？(5)若f(u)为任意函数，(x)ϕ为周期函数，试问f((x)ϕ)是否一定是周期函数？8．判断下列命题是否正确，为什么？(1)若f(x)在]，[βα∀(a,b)⊂上有界，则f(x)在(a, b)上有界.(2)设f(x)在[a, b]上有定义，且在(,)[a,b]∀αβ⊂上有界，则f(x)在[a, b]上有界. 9．适合下列条件的函数存在吗？为什么？(1)在R=(-∞, + ∞)上严格递增的有界函数.(2)在R=(-∞, + ∞)上严格递增的偶函数.(3)在R=(-∞, + ∞)上严格递减的奇函数.(4)在(- , )内为偶函数，且在R=(-∞, + ∞)上又为奇函数.(5)在R上严格递增的周期函数.10．设f(x)在R上有定义，且满足f(x)≠0，f(x·y)=f(x)·f(y)，试求f(1990). 11．用肯定语气叙述：在(-∞, + ∞)上(1)f(x)不是偶函数；(2)f(x)不是周期函数；(3)f(x)不是单增函数；(4)f(x)不是单调函数.12．用肯定语气叙述：(1)f(x)在[a, b]上无下界；(2)f(x)在[a,b)上没有零点；(3)f(x)在(a, b)上没有比中点函数值大的点.13．若f(x)是一一对应的奇函数，试证其反函数也是奇函数.14．设f(x)满足关系式2f(x)+1kf()x x=(k为常数)，证明：f(x)为奇函数.15．设f(x)为(-∞, + ∞)上的奇函数，且在[0,)+∞上严格增，求证：f(x)在(-∞, +∞)上严格增.16．设0a1≤≤，函数f(x)及g(x)对任意的12x,x分别满足1212f[ax (1a)x ]af (x )(1a)f (x )+-≥+-及 1212g[ax (1a)x ]ag(x )(1a)g(x )+-≤+-且g(x)为单减函数，试证：1212g[f (ax (1a)x )]ag[f (x )](1a)g[f (x )]+-≤+-.17．设f(x)在(-∞, + ∞)上严格增，且恒有f[f(f(x))]=f(x)，试证：必有f(x)=x. 18．若f(x)是在(-∞, + ∞)上单增的偶函数，且f(0)=0，则f(x)≡0. 19．若f(x)满足条件：对x R ∀∈有f(x + )=-f(x) ( >0)，证明：f(x)是以 为周期的函数. 20．设常数a>0，函数f(x)0≠，且f(x + a)=1f (x)，x R ∈，试证：f(x)是以2a 为周期的周期函数.21．若y=f(x)(x R ∈)的图形关于两直线x=a 与x=b(a<b)对称，试证f(x)为周期函数. 22．设f(x)和g(x)分别是以 1和 2为周期的函数，且12nm= (m, n 为互质的正整数)，证明：F(x)=f(x)+ g(x)， G(x)=f(x)·g(x)，是以 =m 1=n 2为周期的函数.23．证明：若f(x)是以T 为周期的周期函数，则f(ax)(a>0)是以Ta为周期的周期函数. 24．函数y=f(x)具有反函数的充要条件是什么？ 25．选择填空：(1)奇、偶函数的定义域一定是________.(A)R (B)关于原点对称的区间 (C)关于原点对称的点集 (D)A 、B 、C 都不对 (2)函数f(x)=cosx |xsinx |e ,x (,)∈-∞+∞是________. (A)有界函数 (B)单调函数 (C)周期函数 (D)偶函数(3)函数 D(x)=1,x 0,x ⎧⎨⎩为有理数为无理数是________.(A)非奇非偶函数 (B)有界函数 (C)非周期函数 (D)偶函数 (E)有界周期偶函数(4)若f(x)为奇函数，则下列________款中的函数也是奇函数. (A)f(x)+ a (a 0≠，为常数) (B)f[f(x)] (C))f(-x)+ a (a 0≠，为常数) (D)f(x)+ f(-x)(5)设f(x)222x ,|x |12x ,|x |1⎧-≤⎪⎨+>⎪⎩，)x (ϕ=2,|x |10,|x |1≤⎧⎨>⎩ ，则复合函数f[(x)]ϕ由_____________款表示. (A)f[(x)ϕ]=2,|x |12,|x |1-≤⎧⎨>⎩ (B)f[(x)ϕ]=6,|x |12,|x |1≤⎧⎨>⎩(C)f[(x)ϕ]=22x ,|x |12,|x |1⎧+≤⎨>⎩ (D)f[(x)ϕ]=222x ,|x |12x ,|x |1⎧+≤⎪⎨->⎪⎩(6)函数y=xx 221+的反函数是____________.(A)22log xy log (1x)=- (B)22y log x log (1x)=--(C)2x y log 1x =- (D)x y lg 1x=- 补充题1．|a |=对吗？(2)如果在 | x | >b 中去掉绝对值记号，应该怎样写？ (3)试用 | a + b |，| a -b | 表示Max{a, b}，Min{a, b}. 2．证明下列不等式： (1)n!>2n (n>3) (2)2n >n 2 (n 5≥) (3)n n ≤(n!)2 (n 3≥)(4)132n 1242n -⋅ (5)n!<nn 12+⎛⎫ ⎪⎝⎭(n>1)(6)若x>-1，则(1 + x)n ≥(1 + nx)(n N ∈) (这个不等式称为Bernoulli 不等式) (7)设i a 0> (i=1, 2, , n)且12a a ⋅ a n =1，则a 1 + a 2 + … + a n ≥n. (8)设a i >0(i=1, 2, …, n)，则12na a a n+⋯≤，12nn111a a a +++ .(9)12n 12n |x x x x ||x |(|x ||x ||x |++++≥-+++ ) (10)设a 1, a 2, …, a n ； b 1, b 2, …, b n 为两组实数，则2n n n 22i i i i i 1i 1i 1a b a b ===⎛⎫⎛⎫⎛⎫≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑ 3．解下列不等式(1)| 2x + 4 | >10； (2)| x(x -1)| <0.1； (3)| x -5 | < | x + 1 | ； (4)| x + 1 | - | x -1|<1； (5)| x + 2 | + | x -2 |12≤; (6)| x + 2 | - | x | >1；(7) 2<1|x 2|+<3. 4．设f(x)=arctgx ，g(x)=tgx ，求f[g(x)与g[f (x)]. 5．设0,x 0f (x)x,x 0≤⎧=⎨>⎩，20,x 0g(x)x ,x 0≤⎧=⎨->⎩，求f [g(x)]; g[f(x)]; f[f(x)]; g[g(x)].6．设x ln(1x),0x 2f (x)2,2x 46x,4x 6+≤<⎧⎪=≤≤⎨⎪-<≤⎩，求f(1), f(2), f(π), f(4.5). 7．验证：1Max{f (x),g(x)}[f (x)g(x)|f (x)g(x)|]2=++-Min |])x (g )x (f |)x (g )x (f [21)}x (g ),x (f {--+=8．设f(x), g(x)在(a, b)上单增，求证： (1)Max{f(x), g(x)} (2)min{f(x), g(x)} 也在(a, b)上单增.9．设f(x)在(0,)+∞上有定义，x 1>0, x 2>0，求证：若f (x)x单增，则f(x 1+x 2)≥f(x 1)+f(x 2). 10．一半径为a 的圆铁片，自中心剪去一角形，将剩余部分(中心角为θ)围成一个无底圆锥，试建立圆锥容积V 与中心角θ之间的函数关系.11．证明：函数f(x)=a x (a>0, a ≠1)，对一切实数x 1≠x 2恒有1212x x 1f ()[f (x )f (x )]22+<+. 12．设x xae be f (x)a b-+=+ (a b ≠-)，证明：f(2x)-f(-2x)=f 2(x)-f 2(-x).13．设f(x)=1xlg1x-+，试证： y zf (y)f (z)f ()1yz++=+. 14．设f(x)=x 32x 1+-，解方程12f ()f ()x 13=-. 15．(1)设f(x+1x )=221x x+，求f(x). (2)设x f (sin )1cosx 2=+，求f(cos x2).16．设f(x)为(-∞, +∞)上的奇函数，f(1)=a ，且对任意x 值均有：f(x+2)-f(x)=f(2)(1)试用a 表示f(2)与f(5)；(2)问a 取什么值时，f(x)是以2为周期的周期函数？ 17．研究下列函数有界性 (1)f(x)=2x1x +； (2)f(x)=x 2分别在(a, b)及(-∞, +∞)上；(3)f(x)=x 2+； (4)f(x)=21x x 1++. 18．在物理及工程技术中还用到“双曲函数”，它们的定义为： 双曲正弦 x x e e shx 2--=双曲余弦 x xe e chx 2-+=双曲正切 x xx x shx e e thx chx e e ---==+ 双曲余切 x xx xchx e e cthx shx e e --+==- 试证：(1)22ch x sh x 1-=(2)sh(x y)shxchy chxshy +=+ (3)22ch2x ch x sh x =+， s h 2x2s h x c= (4)2211th x ch x=-(5)1sh x ln(x -= (-∞<x<+∞)1ch x ln(x -= (x 1)≥第二章 数列极限思考题：1．下列说法能否表明a 是数列{}n a 的极限(与n n lim a a →∞=的定义是否等价？)(1)对0∀ε>，N ∃，当n N >时，有n a a -<ε. (2)对0∀ε>，存在无限多项n a ，使n a a -<ε. 3)对0∀ε>，N ∃，当n ≥N 时，有n a a -<ε. (4)对0∀ε>，N ∃，当n >N 时，有100n a a -<ε.(5)对0∀ε>，N ∃，当n >N 时，有n a a k -<ε，(其中k 是与ε，n 无关的常数). (6)对0∀ε>，N ∃，当n >N 时，有n a a N -<ε. (7)对0∀ε>，A R ∃∈，当n >A 时，有n a a -<ε. (8)N ∃，对0∀ε>，当n>N 时，有n a a -<ε.(9)对()a,∀ε∈+∞(a>0)，N ∃，当n>N 时，有n a a -<ε. (10)对∀ε：01<ε<，N ∃，当n>N 时，有n a a -<ε. (11)对无限个ε>0，N ∃，当n>N 时，有n a a -<ε. (12)对m N ∀∈，N ∃，当n>N 时，有n 1a a m-<. (13)设k 0ε→()k →∞，0k >ε，对每个k ε，k N ∃，当k n N >时有n a a -<εk . 2．有人说，n n lim x a →∞=定义与“对(,)∀αβ(a (,)∈αβ)，∃N ，当n>N 时，有n x (,)∈αβ”等价，对吗？3．一个数列去掉或添加或改变有限项是否会改变它的收敛性与它的极限值？ 4．证明：设a, b 为两个定数，(1)若对0∀ε>都有 a b ≤+ε，则a b ≤； (2)若对0∀ε>都有 |a b |-<ε，则a=b.5．若{a n }收敛，{b n }发散，则{a n ±b n }、{a n b n }收敛性如何？举例说明. 6．{a n }与{b n }均发散，则{a n ±b n }、{a n b n }是否发散？举例说明.7．若n n lim a a →∞=，是否必有n 1n lim a a +→∞=？又能否断定n 1n na lim1a +→∞=.8．若对0∀ε>，∃N ，当n>N 时，就有n 1n |a a |+-<ε，则{a n }是否收敛？ 9．下列命题是否正确？为什么？(1)设n n lim a 0→∞=，{b n }为任意数列，则n n n lim a b 0→∞=.(2)若n n n lim x y 0→∞=，则可断定或n n lim x 0→∞=或n n lim y 0→∞=.(3)n n n n lim x 0lim |x |0→∞→∞=⇒=.(4)若{a n }收敛于a ，则将a n 的顺序重新排列后所得的数列{'n a }仍收敛于a. 10．下面的计算方法有无错误，原因何在？ (1)1=n n n n 111limlim ()n n n n →∞→∞=+++个=n n 11limlim 0n n→∞→∞++= . (2)n n n 1111lim(1)lim[(1)(1)(1)]n n n n→∞→∞+=+++ =n n n 111lim(1)lim(1)lim(1)1n n n→∞→∞→∞+++= . (3)n n 111lim(1)(1)(1)111n 1n 22n→∞---=⋅++ 个=1. (4)假设n n lim q a(q 1)→∞=>，则因n 1n q q q +=⋅，两边同时取极限得：q=q a ⋅，从而a=0，故有n n lim q 0→∞=(q>1).(5)n lim 10nn limn n 1→∞==.11．若n n n lim(y x )0→∞-=，n n lim x a →∞=，求证n n lim y a →∞=，请看下面的证法是否正确？n n n n n n n 0lim(y x )lim y lim x →∞→∞→∞=-=- =n n lim y a →∞-n n lim y a →∞∴=.定义：在给定的数列a 1, a 2, …，a n , …中，如果任意地挑选出无穷多项，并按照原有的次序排列出1n a , 2n a , …, k n a , … (n 1<n 2<…<n k <…)就得到一个足标为k 的数列{k n a }，称为原数列的子数列.12．若数列{a n }的两个子列{a 2n }与{a 2n -1}都收敛，则{a n }是否也收敛？ 13．举例给出满足下列要求的数列 (1)无界数列，但不趋于无穷； (2)非单调的收敛数列； (3)无收敛子列的数列.14．若把满足柯西准则条件的数列叫做柯西列(或基本列)(1)若对∀ε>0，N ∃，当n>N 时有n N |a a |-<ε，能否断定{a n }为柯西列？ (2)若对∀ε>0和p N,N ∈∃，当n>N 时有n p n |a a |+-<ε， 能否断定{a n }为柯西列？(3){a n }、{b n }为两个柯西列，能否断定{a n +b n }、{a n b n }也是柯西列？ 15．下面的证法有无错误？设n 11x 12n =+++ ，(n=1, 2, …)，证明n {x }收敛.证：n p n 11|x x |n 1n p+-=++++ <11pn 1n 1n 1+⋯+=+++ 0∀ε>，取p N [1]1=-+ε，则当n N >时，就有n p n |x x |+-<ε.根据柯西准则知数列{x n }收敛.16．用“ε—N ”语言叙述{a n }不是柯西列.17．数列{x n }收敛的充要条件有哪几个？ 18．证明数列{x n }发散有哪些方法？ 19．用肯定语气叙述 (1){x n }不是单调数列； (2)数列{x n }无上界；(3)区间[a, b]上每个数都不是数列{x n }的极限； (4)n n lim x →∞≠+∞.20．若对任给0x R,0∈∃ε>，对N ∀∈N ，0n N ∃>，使0n 0|x x |-≥ε,能说明数列{x n }具有什么性质？22．证明：若n n lim x →∞=+∞，则在{x n }中至少有一项0n x ，使0n n x x ≤ (n=1, 2, …).23．选择填空(1)若{a n }有界，则{a n }_________.(A)收敛 (B)发散(C)可能收敛，也可能发散 (D)A 、B 、C 中结论都不对 (2)若{a n }无界，则{a n }___________.(A)为无穷大量 (B)发散(C)可能收敛，也可能发散 (D)A 、B 、C 中结论都不对 (3)若{a n +b n }发散，则____________.(A){a n }、{b n }都发散 (B){a n +b n }无界(C){a n }与{b n }中至少有一个发散 (D)A 、B 、C 中结论都不对 (4)若n n lim a a →∞=，n n lim b a →∞=，则数列a 1, b 1, a 2, b 2, …, a n , b n , …_________.(A)收敛，但极限未必是a (B)一定收敛于a(C)未必收敛 (D)A 、B 、C 中结论都不对 (5)设{a n }中有无穷多项a n =1，则{a n }=__________.(A)可能是正无穷大量 (B)可能是无穷小量 (C)一定收敛于1 (D)A 、B 、C 中结论都不对 (6)若{a n }中有无穷多个子列都趋于a ，则{a n }___________. (A)一定收敛于a (B)可能是无穷大量 (C)未必收敛，但一定不是无穷大量 (D)A 、B 、C 中结论都不对 (7)设非常数数列{a n }收敛，且n n lim a a →∞=，则___________.(A){a n }为单调有界数列(B){a n }非单调有界数列(C)在{}n a 中必存在一个子列是单调有界数列 (D)在{}n a 中不一定存在单调有界的子列 补充题1．按定义证明下列极限(1)22n n n 51lim 33n 2n 4→∞-+=+- (2)()[]n lim ln n 1ln n 0→∞+-=2．求下列极限(1)n lim(2)n 12n n lim n 22→∞+++⎛⎫- ⎪+⎝⎭ (3)NN n 11lim12n →∞=+++∑ (4)222n 132n 1lim n n n →∞-⎛⎫+++ ⎪⎝⎭(5)2n n 132n 1lim 222→∞-⎛⎫+++ ⎪⎝⎭(6)n lim (7)()()()()n242n lim 1x 1x 1x 1x →∞++++ (|x|<1)(8)nn n a lim 1a →∞+ (a 1≠-)(9)nn 1n a lim 1a a -→∞+++ (a>0)(10)n 1lim n→∞(11)34n 33n n 1lim n 2→∞⎛⎫- ⎪-⎝⎭(12)n lim(13)nn k lim →∞=(14)(n lim →∞(15)222n 111lim 11123n →∞⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(16)n lim(17)2n n lim→∞(18)n 111lim n 1n 22n →∞⎛⎫+++ ⎪++⎝⎭提示：利用n 11lim 1ln n C 2n →∞⎛⎫+++-= ⎪⎝⎭C 为欧拉常数(19)nn k 1lim →∞=∑ (提示：利用两边夹定理)(20)m 22m n lim 1m →∞⎛⎫-⎪⎝⎭(21)(n lim sin →∞3．设{}n a 为正项数列，且n 1n na lim0a +→∞=，证明{}n a 当n 充分大后为单调数列.4．证明：若数列{}n a 无上界，则必有严格增加且趋于+∞的子数列. 5．若nn na limb →∞= ( ≠0)且n n lim a 0→∞=，则n n lim b 0→∞=.6．设数列{}n a 满足n 0a 1<<，()n n 111a a 4+->，证明{}n a 单调增加，且n n 1lim a 2→∞=.7．设{}n a 为单调数列，它的某一子列k n a a →()k →∞，试证n n lim a a →∞=.8．设n n lim x a →∞=，n n lim y b →∞=，求证n n n lim Max(x ,y )Max(a,b)→∞=.9．利用柯西收敛准则，判断下列数列{}n a 的收敛性. (1)()n cos1cos2!cos n!a 1223n n 1=+++⋅⋅+ (2)()()()n a cos 2bsin 2a cos3bsin 3a cos n bsin na 22sin 2!33sin 3!n n sin n!+++=++++++ (a ，b 是常数)(3)n h h h111a 123n =++++(h ≤1) (4)n 111a ln 2ln3ln n=+++(n=2，3，…)(5)若对n ∀≥1，有n 2n 1a a ++-≤n 1n 1a a 2+-，证明{}n a 收敛. 10．试证：n n x x x sin xlim cos cos cos 24x 2→∞= .11．利用单调有界定理求证下列极限 (1)求数列n n!a (2n 1)!!=- (n=1，2，…)的极限.(2)设数列{}n x 满足1x 1<，且()n n 12x x 1+-=，求n n lim x →∞.(3)证明数列n 2n 111x 111222⎛⎫⎛⎫⎛⎫=+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭收敛.12．设n a 0>(n=1，2，…)且n n lim a a →∞=，证明：(1)n 12nnlima 111a a a →∞=+++ ，(2)n lim a =.13．设n a 0>(n=1，2，…)且n 1n na lim a a +→∞=，证明：n lim a .14．设{}n a 为单增数列，12nn a a a S n+++= ，试证：若n n lim S a →∞=，则n n lim a a →∞=.例题：例1．试证：n 11x 1ln n 2n =+++- 收敛(其极限值称为欧拉常数).证：nn n k 1k 2123n 1k 1x ln ln k 12n 1k 1k 1n ==⎛⎫⎛⎫=-⋅⋅=-+ ⎪ ⎪---⎝⎭⎝⎭∑∑ 而 ()k 11k 111ln 1ln 11ln e 0k 1k 1k 1k 1k-⎡⎤⎛⎫-=-+>-= ⎪⎢⎥----⎝⎭⎣⎦ (注意k 11k ⎛⎫+ ⎪⎝⎭严格增且趋于e) ∴ n x 0>，(n=1，2，…)又 n 1n 1n 1n 11x x ln 1ln 10n 1n 1n 1n ++⎛⎫⎛⎫-=+=-+< ⎪ ⎪+++⎝⎭⎝⎭ (∵n !11n +⎛⎫+ ⎪⎝⎭↘且→e(当n →∞时))可见{}n x 为单调减少，且有下界的数列，所以收敛. 记其极限值为C ，故有n 11lim 1ln n C 2n →∞⎛⎫+++-= ⎪⎝⎭.例2．设110a b <<，n 1n 1n n 1n 12a b a a b ----=+，n b (n=2，3，…)，试证{}n a 单增，{}n b 单减，且有相同的极限.证：①先证n a ≤n b 由n n n 1n 1a b --=≤1 立明. ②次证{}n a ↑ 2n n n n n n 1n nn nnn 2a ba b a a a a a b a b +--=-=++≥0 ∴n 1a +≥n a ③再证{}n b↓ n 1b +=n b从而有 1a ≤n a ≤n b ≤b 1，(n=1，2，…) {}n a ⇒，{}n b 都收敛，设n n lim a a →∞=，n n lim b b →∞=.⇒b>0④后证a=b在n b中令n →∞得ba 0=， ∵b 0≠ ∴a b =. 例3．证明施笃兹(stolz)定理.设 1)n 1n y y +> (n=1，2，…) 2)n n lim y →∞=+∞ 3)n n 1n n n 1x x limy y -→∞---a =则 n n n 1n n n n n 1x x x limlim a y y y -→∞→∞--==-.证：对0∀ε>，N ∃，当n N >时有n n 1n n 1x x a y y 2---ε-<-.于是下面的分数N 1N N 1N x x y y ++--，N 2N 1N 2N 1x x y y ++++--，…，n 1n 2n 1n 2x x y y ------，n n 1n n 1x x y y ----都在a 2ε-和a 2ε+之间，从而 n N n N x x a a 2y y 2-εε-<<+- 即n N n N x x a y y 2-ε-<-又N N N n N n n n n n N x ay y x x x a 1a y y y y y --⎛⎫⎛⎫-=+-- ⎪ ⎪-⎝⎭⎝⎭可得nn x a y -≤N N n N n n Nx ay x x a y y y --+-- 由上知，当n N >时，右端第二项小于2ε. 又当n →∞时，第一项→0，故N '∃≥N ，当n N '>时，第一项2ε<，于是，当n N '>时，有nnx a y -<ε. ∴ nn nx lima y →∞=.注1：若将条件3)改为n n 1n n n 1x x limy y -→∞--=+∞-(或-∞)，结论仍然成立.注2：(型stolz 定理)设对一切充分大的n ，{}n b 严格递减，且n n n n lim a lim b 0→∞→∞==，若n n 1n n n 1a a limb b +→∞+--存在，则nn na limb →∞也存在，且n n n 1n n n n n 1a a a lim lim b b b +→∞→∞+-=-.证：设n n 1n n n 1a a limS b b +→∞+-=-，则对0∀ε>，N ∃，当n N >时有n n 1n n 1a a S Sb b ++--ε<<+ε- ⇒()()()()n n 1n n 1n n 1S b b a a S b b +++-ε-<-<+ε- 把上式中n 改为n+1，n+2，…，n+p -1，并把结果相加得 ()()()()n n p n n p n n p S b b a a S b b +++-ε-<-<+ε- 当p →∞时，上式取极限得 ()n S b -ε≤n a ≤()n S b +ε 故当n N >时，有nna Sb -≤ε. ∴ nn na limS b →∞=.注3．应用stolz 定理立得 (1)若n n lim a a →∞=，则12nn a a a lima n→∞+++= .(2)k k k k 1n 12n lim n +→∞+++ (k ≥0)1k 1=+. (3)若()n 1n n lim a a a +→∞-=，则nn a lima n→∞=.(4)设有两个数列{}n a ，{}n b 且n b 0>，nk n k 1lim b →∞==+∞∑，则有12n n n n 12n na a a alimlim b b b b →∞→∞+++=+++ .(5)设k a 0>，nk n k 1lim a →∞==+∞∑，n n lim b b →∞=，则1122n nn 12na b a b a b limb a a a →∞+++=+++ .(6)设n {x }满足n n 2x x 0(n )--→→∞，则n n 1n x x lim0n -→∞+=.(7)设数列n {s }，令01nn s s s ,(n 0,1,2,)n 1+++δ==+对n 1≥，再设n n n 1a s s -=-，证明：若n n lim na 0→∞=，且n {}δ收敛，则n {s }也收敛，且n n n n lim s lim →∞→∞=δ.(提示：nn n k k 11s Ka n 1=-δ=+∑ ，再用stolz 定理)(8)若n n lim a a →∞=，则12nn a 2a na lima 12n→∞+++=+++ .(9)若n n lim a a →∞=则12n 2n a 2a na alim2n →∞+++= .例4．证明：n 111lim(1)e 1!2!n!→∞++++= . 证：记n 2n n 11n(n 1)11x (1)1n ()()n n 2!n n-=+=++++=1111211k 12(1)(1)(1)(1)(1)2!n 3!n n k!n n -+-+--++-- 112n 1(1)(1)(1)n!n n n-++--- 11112k 12(1)(1)(1)(1)2!n k!n n n->+-++--- 固定k ，令n →+∞，在上式两端取极限111e 22!3!k!≥++++ 于是当k=n 时n 111e 2x 2!3!n!≥++++> 而n n lim x e →∞=，n 11lim(2)e 2!n!→∞∴+++= 例5．证明n lim sin n →∞不存在.证：“反证法” 假定{sin n}收敛，设n lim sinn a →∞=.则n lim sin(n 2)a →∞+=，有n n lim[sin(n 2)sinn]lim 2sin1cos(n 1)0→∞→∞+-=+=n lim cos(n 1)0→∞⇒+=， n l i m c o s n 0→∞⇒= n n lim sin2n lim 2sinncosn 0→∞→∞⇒==a 0⇒=从而n n lim sin n 0,lim cosn 0→∞→∞==n lim sin n →∞∴不存在.例6．设n n lim a a →∞=，n n lim b b →∞=，证明：1n 2n 1n 1n a b a b a b limab n -→∞+++= .证：由n a a →，n b b →可得n a c,(n 1,2,)≤=12n n a a a a a aA 0n -+-++-=→12n n b b b b b bB 0n-+-++-=→故对0,N ∀ε>∃，当n N >时，n n A ,B <ε<ε,从而当n N >时，有1n 2n 1n 11nn 1a b a b a b (a b ab)(a b ab)ab n n-+++-++--= =1n 11n 1n n (a b a b a b ab)(a b a b a b ab)n-+-++-+-1n 2n 1n 112n a (b b)a (b b)a (b b)(a a)(a a)(a a)b n n--+-++--+-++-≤+ n n cB b A c b (c b )≤+<ε+ε=+ε1n 2n 1n 1n a b a b a b limab n-→∞+++∴= .例7．证明a n log nlim0n→∞= (a 1)>.证：对0a 1ε∀ε>⇒>n l i 1= ，故N ∃，当n>Na ε从而a 1l o g n n<ε 即当n>N 时有a a 11log n 0log n n n-=<ε a n 1limlog n 0n→∞∴=. 例8．若已知n limln p n→∞= (p>0，为常数)，求nn lim (3→∞ (a>0，b>0，c>0).解：n(3=3(13⎡+⎢⎢⎥⎣⎦=ln[(1∴原式=1h n n 1lim lim (1h)]3n n n e→∞→∞+(其中n 3h 03→∞=−−−→) =1[lna ln b lnc]lne 3e ++=1lnabc 3e =第三章 函数极限思考题1．函数极限x alimf(x)A →=定义与下列形式是否等价？为什么？(1)n 1,02∀∃δ>，当0x a <-<δ时，n1f (x)A 2-<. (2)10,0n ∀ε>∃>，当10x a n <-<时，f (x)A -<ε.(3)0,0∀ε>∃δ>，当0x a <-<εδ时，f (x)A -<ε. (4)0,0∀ε>∃δ>，当0x a <-<δ时，f (x)A -<. (5)0,0∀ε>∃δ>，当0x a <-<δ时，f (x)A -<δε. 2．f(x)在a 点极限与f(x)在a 处的情况是否有关？3．定义：称a D ∈为D 的孤立点，当且仅当存在开区间I ，使I D {a}⋂=. 试问，讨论f(x)在a 点极限时，a 可否是f(x)定义域的孤立点？4．若对0,0∀ε>∃δ>，当x a -<δ时，有f (x)A -<ε，试问，x alimf(x)→是否存在？如果存在，极限值A 等于什么？5．0∀ε>，对0∀δ>，当0x a <-<δ时，均有f (x)A -<ε，问f(x)的变化情况如何？6．若0∃ε>，对0∀δ>，当0x a <-<δ时，有f (x)A -<ε，问f(x)的变化情况如何？7．对:01,:01∀ε<ε<∃δ<δ<，当0x a <-<δ时，有f (x)A -<ε， 问x alimf(x)→=A 成立否？8．设0x x lim f (x)→=A ，且f(x)在x 0点有定义，问在x →x 0的过程中是否可以取x=x 0? f(x)能取值A 吗？又是否必有A=f(x 0)?9.试用“ε-δ”语言写出当x →x 0+时，f(x)不以A 为极限.10．若x 0lim +→f(x)=A ，则是否成立n 1lim f ()A n →∞=？反之是否成立？11．举出满足下列各要求的例子.(1)虽然x 0lim →f(x 2)存在，但x 0lim →f(x)不存在；(2)0x x lim f (x)→存在，但0x x lim →f(x)不存在；(3)f(x)在其定义域内每一点都不存在极限； (4)f(x)在其定义域内仅在一点极限存在. 12．选择填空：(1)若f(x)在点x 0的某邻域内有界，则0x x lim →f(x)________.(A)存在 (B)不存在 (C)未必存在(2)若f(x)在点x 0某邻域内无界，则0x x lim →f(x)________.(A)存在 (B)不存在 (C)可能存在 (3)若0x x lim →f(x)存在，则f(x)在x 0点处 定义.(A)有 (B)无 (C)不一定有13．设f(x)在D 上有定义，则f(x)在D 上无上界的充要条件是：n x D ∃∈(n=1, 2, …)，使n n lim f (x )→∞=+∞.14．若对()0,M 0,∀ε>∃ε>使当x>M 时，有f (2x)f (x)-<ε，则x lim →+∞f(x)是否一定存在？15．下列说法是否正确？(1)无穷小量是非常小的量；无穷大量是非常大的量； (2)无穷小量小于任何实数；无穷大量大于任何实数； (3)无穷大量总大于无穷小量；(4)无穷大量与有界量的乘积是无穷大量；(5)两个无穷大量之和仍为无穷大量； (6)无穷大量与无穷小量的乘积为无穷小量； (7)无穷大量与无穷小量的乘积为无穷大量. 16．证明f(x)在x 0点极限不存在，有哪些常用的方法？17．若f(x)在(x 0, x 0+η)(η>0)上单增有上界，问0x x lim +→f(x)是否存在？18．下列算法是否有误？错在哪里？ (1)x 0sin x 0lim1x 0→==；(2)2x x x lim 12→∞+∞==+∞； (3)x x 1lim(1)11x ∞→∞+==； (4)33x 0x 0tgx sin x x xlimlim 0x x →→--==；(5)x x x tgx tgx xlimlim lim 1sin x x sin x→π→π→π=⋅=；(6)22x 0x 0x 0x 0111lim x sinlim x limsin 0limsin 0x x x→→→→=⋅=⋅=；(7)x 0x 01sin 1x lim x sinlim 11x x→→==；(8)2x 3x 3x 3x 3x 3lim(x 3)lim(x 3)x 9limlim(x 3)6x 3lim(x 3)→→→→→-⋅+-==+=--. 19.设f(x)=3x ,x 12,x 1⎧≠⎨=⎩，证明：()x 1limf x 1→=.试问下面两种证法是否有错误？证法1：当x ≠1时，32f (x)1x 1x 1x x 1-=-=-⋅++先设 0<x 1-<1，这时()x x 112f x 1x 1≤-+<⇒-=-2x x 17x 1⋅++≤-对0,7ε∀ε>δ=取，则当0<x 1-<δ时 ()f x 1-<ε()x 1limf x 1→∴=.证法2：当x ≠1时，()2f x 1x 1x x 1-=-⋅++ 令2x 1,x x 13≤++≤则，要使 ()f x 13x 1-≤-<ε，只要0<x 13ε-<， 对0∀ε>，取min{1,}3εδ=，则当0|x 1|<-<δ时，有()f x 1-<ε()x 1limf x 1→∴=.补充题 1．求下列极限(1))x lim x →-∞；(2)x →(3)x 0limx→(4)x lim→； (5)x 2x x lim ;1x →∞⎛⎫ ⎪⎝⎭+ (6)2x 0cosx cos3xlimx →-(7)3x 0tgx sin xlimx →-； (8)()x 1xlim 1x tg;2→π- (9)2x 01cosxcos2xcos3xlim ;sin x→-(10)x →(11)()2ctg x2x 0lim 13tg x ;→+(12)x 01lim x x →⎡⎤⎢⎥⎣⎦；(13)()x a 0→>(14)()1xx x x12n i x 0a a a lim a 0n→⎛⎫++⋯+>⎪⎝⎭.2．讨论单侧极限(1)()x 21,0x 12f x x ,1x 22x ,2x 3⎧<≤⎪⎪=<<⎨⎪<<⎪⎩ ，在在0，1，2三点. (2)()111f x x x x n⎡⎤=-=⎢⎥⎣⎦在各点. 3．证明下列关系式31x 4(x →0).(2)sin 2~nπ(n →∞). (3)22sin x 1O 1x x ⎛⎫= ⎪⎝⎭+ (x →∞). (4)42x 21o x 3x +⎛⎫= ⎪⎝⎭+ (x →∞). 4．设f(x)在(a,+∞)上单调上升，n n lim x →∞=+∞，若()n n lim f x A →∞=，求证：x lim f(x)A →∞=. (A 可以为无穷)5．设f(x)在(a,+∞)上严格增，若()()n n x lim f x lim f x →∞→∞=，求证：n n lim x →∞=+∞.6．设f(x)在[a,b]上严格递增，如果对于x n ∈[a,b],(n=1, 2, …)有()()n lim f x f a →∞=成立，则 n n l i m x a →∞=.7．设f(x)是(),-∞+∞上的周期函数，又()x lim f x 0→∞=，求证：()f x 0≡.8.设32x 1x ax x 4lim x 1→---++有有限极限值L ，试求a=? L=?9．设()f x 在点0x 的某邻域()0U x (点x 0可能例外)内有定义， 试证：如果对任意点列()()}{n n 0n 0n 10n 0x x U x ,x x n ,0|x x ||x x |+∈→→∞<-<-都有()n n lim f x A →∞=，则0x x lim f (x)A →=. [提示：可用反证法]10．证明：若mi i 1a 0==∑，则mi x i 1lima 0→+∞=∑.第四章 函数的连续性函数f(x)在点x 0连续有下列各种等价叙述 (1)()()00x x lim f x f x →=.(2)0,0∀ε>∃δ>，()()00x :x x f x f x ∀-<δ⇒-<ε. (3)()()()000x 0lim y 0,x x x ,y f x x f x ∆→∆=∆=-∆=+∆-其中.(4)()()()000f x 0f x 0f x +=-=. (5)n n 0x :x x ∀→，有()()n 0n lim f x f x →∞=.(6)()[]()()000,0f U x ,U f x ,∀ε>∃δ>⇒δ⊂ε.引进记号：用C[a,b]表示定义在[a,b]上所有连续函数全体. 思考题：1．(1)试用“ε-δ”言语写出f(x)在x=x 0点左连续的定义.(2)如果极限()0x x lim f x →存在，那么f(x)在x 0点是否连续，若不连续，有哪些可能的间断情况？2．能否补充定义f(0)，使得下列函数f(x)在x=0点连续？ (1)f(x)=()1x1x ,+ x ≠0. (2)()1x f x e ,= x ≠0. (3)()f x x ≠0.3.证明(1)设对于所有的x ，函数f 满足()f x x ≤，则f(x)在x=0点连续. (2)设函数g 在0点连续，且g(0)=0及()()f x g x ≤，则f(x)在x=0连续. (3)设f 只可能有可去不连续点，定义g(x)=()y xlim f y ,→则g(x)为连续函数.(4)设y=f(x)在(),-∞+∞上满足f(x+t)=f(x)+f(t)，且在x=0点连续，则f(x)在(,-∞+∞)上任一点a 处连续.4．设在点x 0处，f(x)连续，g(x)不连续，问f(x)+g(x)与f(x)⋅g(x)在x 0点是否连续？若f(x)与g(x)在点x 0处都不连续，结果怎样？5．试作出两个处处不连续的函数的复合函数是处处连续函数的例子. 6．试作出一个定义在(),-∞+∞上只有两个连续点的函数.7．作一函数f(x)，使它在(),-∞+∞处处不连续，而()f x 在(),-∞+∞上处处连续. 8．设()1,x g x 0,x ⎧=⎨⎩为有理数有无理数，[]x 1,1∈-，研究函数x ⋅g(x)，x [1,1]∈-的连续性.9．设()[]()()f x C a,b f a f b ∈<且，则它的值域是否就是()()[]f a ,f b ？ 若f(x)在[a,b]上还是单增的，结果如何？10．若f(x)在[a,b]上仅有一个()0x a,b ∈第一类间断点，证明f(x)在[a,b]上有界. 11．试举例说明，根的存在性定理(零值定理)对于在[a,b]上有定义，在(a,b)内连续的函数不一定成立.12．若f(x)是连续的奇函数，则f(x)至少有一个根. 13．设f(x)在(a, b)内连续，且恒为正，a<x 1<x 2<… <x n <b ，证明：至少存在一点()a,b ζ∈，使()f ζ= 14．设f(x)，g(x)∈C[a,b]，且f(a)>g(a), f(b)<g(b)，求证：在(a,b)内至少有一点ζ，使()()f g ζ=ζ. 15．设f(x)在(),-∞+∞上连续，且f[f(x)]=x ，求证：存在()0x ,∈-∞+∞，使()00f x x =.16．若()[]f x C a,b ∈，且对任何x [a,b]∈，存在相应的()y a,b ∈使得()()1f y f x 2≤，则至少存在一点[]a,b ,ζ∈ 使()f 0ζ=. 17．设()[]f x C a,b ∈，令()t f (x),f x t,⎧=⎨⎩()[]()[]f x t x a ,bf x t x a ,b>∈≤∈的的，求证：()[]t f x C a,b ∈. 18．设f(x)，g(x)∈C[a,b]，若在一切有理点x ∈[a,b]上f(x)=g(x)，证明：在[a,b]上()()f x g x ≡.19．研究函数()0,x 0f x 1p ,x ,p,q q q⎧⎪=⎨=⎪⎩当为大于的无理数当为互质的正整数 的连续性. 20．设f(x)在x=0处连续，且对()12x ,x ,∀∈-∞+∞恒有()()()121212f x x f x f x 2x x +=+-证明：(1)f(c)=0.(2)f(x)在(),-∞+∞上连续.21．设f(x)C(0,)∈+∞，且满足f(x 2)=f(x)，(x>0)证明：f(x)为一常数.22．设f (x)C [0,1]∈，值域为[0,1]，则至少存在一点[]x 0,1∈，使()f x x =.23．若()[]f x C a,b ∈且f(x)恒为有理数，问f 应为怎样的函数？24．设f(x)满足介值性，并且对每一值，f 只取得一次，证明f 是连续的.25．设f 是连续函数，且()()n nx x f x f x lim lim 0x x →+∞→-∞==，证明： 当n 是奇数时，必有一数ζ满足()n f 0ζ+ζ=.26．设f(x)在[a,b]上递增，且有介值性，证明f (x)C[a,b]∈.27．设f (x)C[a,b]∈，且f(a)=f(b)，证明： 一定存在0a b x [a,]2+∈，使00b a f (x )f (x )2-=+. 28．下面说法是否成立？为什么？(1)若f(x)分别在[a,b]与[c,d]上都一致连续，则f(x)在[a,b]⋃[c,d]上也一致连续.(2)若f(x)分别在(a,b)与(b,c)上均一致连续，则f(x)在(a,b)⋃(b,c)上也一致连续.(3)若f 和g 在区间I 上一致连续，则f (x)g(x)±在I 上也一致连续.29．有人说：若f(x)在[a,)+∞上一致连续，则x lim f (x)→+∞必存在，对吗？ 30．证明：若f(x)在(a,b)内连续，单调有界，则f(x)在(a,b)内一致连续. 若在条件中将单调去掉，结论是否还成立？31．证明：设f 在(a,)+∞上连续，且当x →+∞时，y=f(x)以直线y=bx+c 为渐近线，即满足x lim [f(x)(bx c)]0→+∞-+=，则f(x)在[a,)+∞上一致连续. (提示：方法1，按一致连续定义证. 方法2，先考虑函数ϕ(x)=f(x)-(bx+c)的一致连续性)补充题：1．试决定常数a, b, c 使函数2ax bx c ,0x 1f (x)1,x 01,x 1⎧++<<⎪=-=⎨⎪≥⎩在(,)-∞+∞上处处连续.2．证明Dirichlet 函数1,x D(x)0,x ⎧=⎨⎩为有理数为无理数在(,)-∞+∞上处处不连续.3．用定义证明x,x f (x)0,x ⎧=⎨⎩为有理数为无理数仅在x=0连续.4．证明：方程x=asinx+b (a>0,b>0)至少有一个正根，并且它不超过a+b.5．设f(x)在(a,b)上连续，极限x a lim f(x)+→与x blim f(x)-→都存在且异号，证明：必有一点(a,b)ξ∈，使f ()0ξ=.6．已知f(x)在[0，1]上非负连续，且f(0)=f(1)=0，则对任意实数(0,1)∈ ，必有点0x [0,1]∈，使00f (x )f (x )=+ .7．设f(x)在(a,b)内连续，若有数列n n n n x ,y (a,b),x a,y a ∈→→,使极限n n l i m f (x )A →∞=，n n lim f (y )B →∞=存在，则对A 与B 之间的任意数μ，必可找到数列n z a →，使n n lim f (z )→∞=μ. 8．若f(x)在[a,b]上只有第一类间断点，则f(x)在[a, b]上有界.9．证明：若f(x)在(a,b)上连续，且f(a+0), f(b -0)存在有限，则f(x)可取到f(a+0)与f(b -0)之间的所有值，但f(a+0),f(b -0)不一定能取到.10．设f(x)在区间I 上有定义，0x I ∈，则f(x)在x 0点连续⇔对n n 0x I,x x ∀∈→，都有n 0n lim f (x )f (x )→∞=. 11．试证：若f(x)为连续但不等于常数的周期函数，则f(x)必有最小正周期.12．设f (x)C[a,b]∈,若数列n x [a,b]∈存在极限n n lim f(x )A →∞=，则必存在0x [a,b]∈,使f(x 0)=A.13．举例(1)有上界无下界的无界集.(2)既无上界又无下界的无界集.(3)有最小上界，无最大下界的数集.(4)含有最小上界但不含有最大下界的数集.(5)既含有最小上界又含有最大下界的数集.14．证明：若f(x),g(x)在有限的区间I 上一致连续，则f(x)·g(x)在I 上一致连续，并举例说明此命题对无限区间不成立.15．证明：若f(x)在(a, b)内连续，且f(a 0)f(b-0)+==+∞，则f(x)在(a,b)内能取得最小值.16．证明：若f(x)在(a, b)上连续：a<c<d<b ，且k, 为正数，则至少存在一点(a,b)ξ∈，使kf (c)f (d)(k )f ()+=+ξ .17．设f(x)定义在(,)-∞+∞上，对x,y (,)∀∈-∞+∞，有f (x y)f (x)f (y)+=+且f(x)在x=0点连续.(1)求f(0)=?(2)证明f(x)为奇函数.(3)证明f(x)在(,)-∞+∞上一致连续.18．用“ε-δ”语言写出f(x)在(a,b)上不一致连续的涵义.19．求证：sin x f (x)x =在(-1，0)和(0，1)上都一致连续，但在0x 1<<上并非一致连续.20．证明：(1)f (x)cosx =在(,)-∞+∞上一致连续. (2)1f (x)sin x=在(0，1)上不一致连续. (3)1f(x)xcos x=在(1,)+∞上一致连续. (4)2f (x)sin x =在(,)-∞+∞上不一致连续. (5)ln(1x)f (x)x+=在(0,)+∞上一致连续. 21．设f(x)为(,)-∞+∞上的周期连续函数，证明：f(x)在(,)-∞+∞上一致连续. 定义：设函数f(x)定义在(a,b)上，若存在常数M>0，使对一切12x ,x (a,b)∈，有2121f (x )f (x )M x x -≤-则称f(x)在(a,b)上满足李普希兹(Lipschitz)条件.22．若f(x)在(a,b)上满足lipschitz 条件，证明f(x)在(a,b)上一致连续.23．设f(x)在[a,)(a 0)+∞>上满足lipschitz 条件，证明f (x)x 在[a,)+∞上一致连续. 24．设f (x )C [a ,b ]∈,且只有唯一的最小值点x 0,又设n x [a,b]∈，有n 0n lim f (x )f (x )→∞=，求证：n 0n lim x x →∞=. 定义：若对[,]I,f (x)∀αβ⊂在[,]αβ上都一致连续，则称f(x)在区间I 上内闭一致连续.25．下列说法是否正确，为什么？(1)若f(x)在有限区间I 上无界，则f(x)在I 上必非一致连续.(2)若f(x)在区间I 上无界，则f(x)在I 上必非一致连续.(3)f(x)在(a, b)上一致连续f (x)⇔在(a, b)上内闭一致连续.(4)f(x)在区间I 上内闭一致连续⇔f(x)在I 上连续.(5)f(x)在区间I 上一致连续⇔对区间I 中满足n n n lim(x y )0→∞-=的任何两个数列n {x }, n {y }总有n n n lim[f(x )f(y )]0→∞-=.第五章 导数与微分思考题：1．是否成立？(1)0000f '(x )[f (x )]';f '(x )f '(x 0)+==+.(2)若0f '(x )存在，则000n 1lim n[f (x )f (x )]f '(x )n→∞+-=. 2．若连续函数f(x)在x=x 0处不可导，问曲线y=f(x)在点(x 0,f(x 0))处的切线能否存在？3．设f(x)在x 0点可导，g(x)在x 0点不可导，问f(x)+g(x)及f(x)·g(x)在x 0点是否可导？4．能否说：初等函数在其定义域内都是可导的？5．若f(x)在x 0点可导，能否推出必存在点x 0的某邻域U(x 0),使f(x)在U(x 0)内可导？6．设f(x)在(,)-∞+∞上有定义，且满足：(1)f(x)=f(x 2), x (,)∈-∞+∞，(2)在x=0点可导,求df(0).7．设f(x)对12x ,x (,)∀∈-∞+∞有f(x 1+x 2)=f(x 1)·f(x 2),且f '(0)=1， 证明：f '(x)=f(x).8．若f(x)在(,)-∞+∞上有定义，且存在常数k 与a>1，使对12x ,x (,)∀∈-∞+∞, 有a 1212f (x )f (x )k(x x )-≤-，证明f(x)为一常数.9．设f(x)在(,)-∞+∞内有连续导函数f '(x)，且x lim f(x)0→∞=，证明：至少存在一点(,)ξ∈-∞+∞，使f '()0ξ=.10．证明：若f(x),g(x)在x=0处可导，且g'(0)≠0，又f(0)=g(0)=0，则x 0f (x)f '(0)limg(x)g'(0)→=. 补充题：1．研究函数①xarctg ,x 0f (x)0,x 0⎧>⎪=⎨⎪≤⎩在x=0点的可导性. ②1x 1,x 01ef (x)0,x 0⎧≠⎪⎪+=⎨⎪⎪=⎩ 在x=0的可导性.2．设23x ,x 0f (x)x ,x 0⎧≥=⎨<⎩ ，求f '(x). 3．设1x e ,x 0f (x)0,x 0-⎧⎪≠=⎨⎪=⎩，你能用几种方法求出f '(0)?4．设f(x)在(,)-∞+∞上二阶导数连续，且f(0)=0，对于函数f (x),x 0g(x)x a,x 0⎧≠⎪=⎨⎪=⎩(1)确定a 的值，使g(x)在(,)-∞+∞上连续.(2)证明确定的a 值，可使g(x)在(,)-∞+∞上一阶导数连续.5．设ϕ(x)当x ≤x 0有定义，并且二阶导数存在，应该怎样选取系数a,b,c ，才能使函数02000(x),x x f (x)a(x x )b(x x )c ,x x ϕ≤⎧=⎨-+-+>⎩的二阶导数存在？ 6．设a 为常数，a 1x sin ,x 0f (x)x 0,x 0⎧>⎪=⎨⎪≤⎩，请回答下列问题： (1)在什么情况下，f(x)不是连续函数？(2)在什么情况下，f(x)是有界函数？(3)在什么情形下，f(x)连续，但不可导？(4)在什么情形下，f(x)可导，但f '(x)不连续？(5)在什么情形下，f '(x)连续？。

青岛科技数学考研真题青岛科技大学的数学考研真题一直备受考生关注和重视。

本文将分为三个主要部分，分别是考研数学真题概述、解题技巧，以及对考研数学真题的总结和建议。

一、考研数学真题概述青岛科技大学的数学考研真题涵盖了多个方向和领域，如高等数学、线性代数、概率统计等。

考研数学真题包括选择题和解答题，旨在考察考生对数学理论和解题思路的掌握程度。

选择题主要考查数学基础和基本概念的理解，而解答题则要求考生运用所学知识解决实际问题。

二、解题技巧1. 培养系统的数学基础知识：正确理解和记忆数学基础知识，掌握各个方向的公式和定理，这对解题至关重要。

2. 高效学习刷题方法：能通过刷题提高解题速度和正确率。

刷题时可以找一些经典的数学教材或者专业考研辅导书进行练习。

题目类型涉及选择题、填空题、计算题等，要注重练习各种类型的题目。

3. 解题思路合理化：考虑到考试时间紧张，考生需要培养快速解题的能力。

在解题过程中，可以采用剖析问题要点、构建数学模型、运用数学方法等思维方式，从而找到解题的切入点。

4. 强化综合应用能力：数学考研真题往往要求将数学知识应用到实际问题中。

因此，要培养综合应用数学知识的能力，将不同的知识点进行有机组合，解决应用问题。

三、考研数学真题总结与建议1. 多做真题：熟悉并掌握真题的题型和出题规律，可以帮助考生更好地备考。

2. 分析错题：仔细分析错误题目的原因，找出自己解题的薄弱点，有针对性地进行复习。

3. 考试技巧：合理安排时间，尽量根据试题的难易程度进行答题顺序的调整，避免在一道难题上花费过多时间。

4. 备考计划：提前制定具体的备考计划，合理安排每天的学习时间，注重知识的系统性和完整性的学习总结：青岛科技大学的数学考研真题是考生备考过程中不可忽视的重要资源。

通过对真题的细致分析和合理备考，考生可以更好地掌握数学基础知识，提高解题效率和准确性。

我们相信，只要你努力备考，合理规划学习时间，坚持解题实践，一定能够在考研数学中取得好成绩。