土基回弹模量与弯沉值的关系
- 格式:pdf
- 大小:59.61 KB
- 文档页数:1

二、土基回弹模量的确定方法回弹模量是指路基、路面及筑路材料在荷载作用下产生的应力与其相应的回弹应变的比值。
车辆荷载通过路面传至土基的垂直压力,使土基产生一定程度的竖向位移变形,假定土基为均质的弹性体,在圆形垂直均布荷载作用下,在应力与应变成直线关系时,可用弹性理论来建立荷载与变形之间的关系式:式中:Lr——路表距离荷载中心袖为r某点处的垂直位移,亦称弯沉值,cmP——圆形垂直均布荷载,MPa;E。
——土基回弹模量,MPa;δ——圆形均布荷载面积半径,m;u——土的泊松系数,取o. 35;a——竖向位移系数,是r/δ的函数, r/δ=0时,a=1;r/δ=1.5时,a=o 356。
由上式看出;在一定的车轮荷载作用下,土基的回弹模量E0值越大,所产生的回弹弯沉值L r就越小。
这标志着土基的承载能力大,抵抗变形的能力强。
土基的强度可用若干指标来表达(如抗剪强度、CBR值、回弹模量等)。
我国是以路表设计弯沉值作为路面整体强度的设计控制指标。
由式(2-7-15)或三层体系理论分析可知,影响路表弯沉的主要因素是路基的强度,70%~95%的弯沉取决于路基。
因此采用土基回弹模量Eo来表示土基的强度。
土基回弹模量确定可以通过现场实测、室内实验法、换算法或通过经验公式计算确定的查表法。
1.现场实测:在不利季节,在已竣工的路基上,用承载板通过逐级加荷卸载的方法测出每级荷载的回弹变形值,并采用间弹变形Lo=0.5~1mm的测定值,参考各地经验的综合式(2-7-16)计算土基回弹模量。
或用弯沉仪测定土基回弹模量值。
详细操作及计算可按《公路路基路面现场测试规程》(JTJ059—95)中T0944一95规定、《公路沥青路面设计视范》(JTJ014-97)中表8执行。
Eo=2430L0-0.7(2-7-16) 1.内实验法:按最佳含水量下制备三组土样试件,测得不同压实度与其相对应的回弹模量值,绘成压实度与回弹模量曲线;查图求得标准压实度条件下土的回弹模量值。
CBR值与弯沉的关系分析公路建设的实际经验表明,70%~95%的路表弯沉取决于路基,而路基填料的CBR值将在很大程度上影响路基的整体强度和刚度,进而对弯沉产生影响,因此有必要对CBR值与弯沉的关系进行充分考虑。
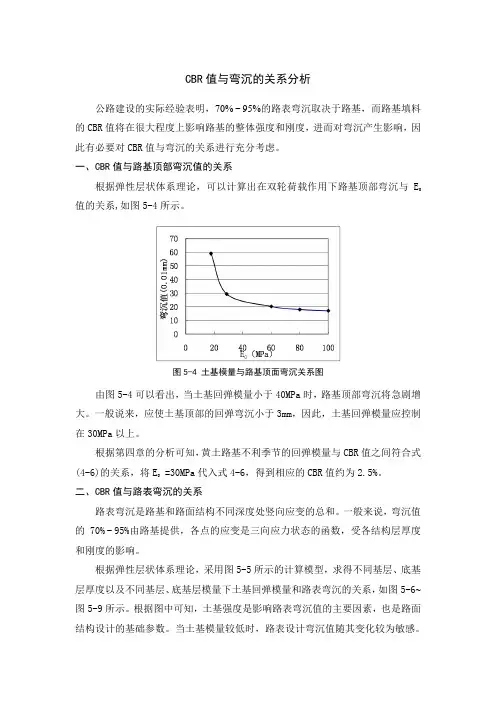
一、CBR值与路基顶部弯沉值的关系根据弹性层状体系理论,可以计算出在双轮荷载作用下路基顶部弯沉与E0值的关系,如图5-4所示。
图5-4 土基模量与路基顶面弯沉关系图由图5-4可以看出,当土基回弹模量小于40MPa时,路基顶部弯沉将急剧增大。
一般说来,应使土基顶部的回弹弯沉小于3mm,因此,土基回弹模量应控制在30MPa以上。
根据第四章的分析可知,黄土路基不利季节的回弹模量与CBR值之间符合式(4-6)的关系,将E0 =30MPa代入式4-6,得到相应的CBR值约为2.5%。
二、CBR值与路表弯沉的关系路表弯沉是路基和路面结构不同深度处竖向应变的总和。
一般来说,弯沉值的70%~95%由路基提供,各点的应变是三向应力状态的函数,受各结构层厚度和刚度的影响。
根据弹性层状体系理论,采用图5-5所示的计算模型,求得不同基层、底基层厚度以及不同基层、底基层模量下土基回弹模量和路表弯沉的关系,如图5-6 图5-9所示。
根据图中可知,土基强度是影响路表弯沉值的主要因素,也是路面结构设计的基础参数。
当土基模量较低时,路表设计弯沉值随其变化较为敏感。
当土基模量大于60MPa时,对路表弯沉的影响将大大减弱。
同时,随着基层、底基层模量的提高以及厚度的增大,土基模量对路表弯沉的影响将逐渐减弱。
对于高速、一级公路而言,当基层、底基层大于25cm,路表弯沉控制在0.4~0.5mm 以内时,土基回弹模量应大于30MPa。
此时,由式4-5,对应的CBR值应大于2.5%。
图5-5 土基模量与弯沉关系计算模型图5-6土基模量及底基层厚度对路表弯沉的影响图5-7 土基模量及基层厚度对路表弯沉的影响图5-8土基模量及底基层模量对路表弯沉的影响图5-9 土基模量及基层模量对路表弯沉的影响。

土基回弹模量与弯沉值的计算吴祖德(常州市建设工程施工图设计审查中心, 江苏常州 213002)内容提要 不同的土基回弹模量有其相应的弯沉值,通过计算、验证,找到适合本地区的经验公式。
本文介绍实际工作中,可使用的两个经验公式,并附常州地区所采用的计算值,供参考。
关 键 词 土基回弹模量 弯沉值1 土基回弹模量与验收弯沉值的换算 1.1“公路沥青路面设计规范”(JTG D50-2006)5.1.8中的公式()202011012⨯-=αμδODOD E K P L (1)式中: OD L —路基设计弯沉值(0.01mm );P ,δ—测定车轮胎接地压强(MPa )为0.7 MPa 与当量圆半径(mm )为106.5mm; μ—土基的泊松比。
一般为0.35 α0—均匀体弯沉系数,取0.712; E OD —路基设计回弹模量(MPa );K 1—不利季节影响系数,可根据当地经验确定。
在实测某路段土基回弹模量后,可通过下式确定某路段土基回弹模量设计值: 100/)(K S Z E E a S -= (2)式中:S E 0—某路段土基回弹模量设计值;0E 、S —某路段实测土基回弹模量平均值与标准差a Z —保证率系数,高速公路、一级公路为2.0;二、三级公路为1.648;四级公路为1.5; 1K —不利季节影响系数,若在非不利季节测定应考虑季节影响系数,并根据当地经验选用。
表1 土基回弹模量与弯沉值的计算结果注:此表是后面的回归式为准时,算出其相应的不利季节影响系数,可比较不同回归式间的差异。
1.2按《公路路面基层施工技术规范》(JTJ 034-2000)附录A 的公式先将土基回弹模量计算值(E 0)按式(3)调整到相当于非不利季节的值(E 0’): E 0’= K 1·E 0 (3)式中:K 1—季节影响系数,不同地区取值范围为1.2~1.4,各地可根据经验确定。
土基顶面的回弹弯沉值,按回归 式(4)计算:L 0=9308938.00E (4)式中:E 0—土基回弹模量(MPa )L 0—土基顶面的回弹弯沉计算值(0.01mm )根据常州地区,土基回弹模量与弯沉值的计算结果如下:序号 E 0(MPa ) L 0(mm ) K 1 1 15 5.35 1.4 2 20 4.09 1.4 3 22 3.74 1.4 4 25 3.32 1.4 5 26 3.20 1.4 6 30 2.79 1.4 7 32 2.63 1.4 8 35 2.42 1.4 9 34 2.48 1.4 10 40 2.13 1.4 11 60 1.46 1.4 12801.111.42历次规范对土基回弹模量的计算公式2.1不同规范中弯沉值L 0回弹模量E 0值表,见表3。

路床完沉值弯沉值=9308E-0.938E路基回弹模量弯沉值作为路基及路面各结构层的强度评价指标已广为接受。
但结构层弯沉值的容许值确定颇具商榷。
一般的参考书籍、交通部颁发现行规范。
验收评定标准对弯沉指标的说明不透彻,甚至相互抵触,很多方面靠人为理解,实际操作困难。
例如,现行《公路工程验收评定标准》(JTJ071-98)对基层、底基层取消弯沉检验指标。
故相当建设项目取消弯沉检测。
而《公路路面基层施工技术规范》(JTJ034-93)第8.4.3、第8.5.6明确规定了弯沉值检验项目作为基层,底基层质量合格标准必检项目。
因此,很有必要对弯沉指标作深入剖析。
理解弯沉的意义,掌握容许弯沉的确定方法。
1、弯沉值的作用弯沉是表征路基或路面各结构层抵抗是、竖直变形的能力。
弯沉值越大,说明结构层强度越低。
弯沉值的作用主要反映在以下三个方面:(1)评价路基或路面结构强度车辆荷载在路基、路面结构中产生的有效作用区通常在1.5~2.0m,路面各结构层顶面检测的弯沉值包含有一定厚度土基及其相应下承层的强度。
因此,弯沉是一个综合反映路基路面整体强度。
这也是世界上很多国家采用弯沉作为沥青路面设计强度指标的原因。
(2)评价路基或路面各结构层次的均匀性即使同一路段,土基填料千差万别,填土高度交替变化,三交地段频繁出现。
这些因素引起路床强度差异显著,最终导致在强度薄弱处首先出现早期局部损坏。
因此,路基、路面各结构层次强度的均匀性正越来越受重视。
其均匀性的控制一方面通过宏观调节,如材料的进场、摊铺、平整、碾压等工艺流程,可采用目视法,随时纠正;另一方面通过具体指标检验评价。
压实度、厚度、平整度等指标均可用作为评价均匀性的辅助指标,但由于检验这些指标的频率很低,如验评标准中抽检基层压实度频率仅要求每200m每车道仅检测2处;施工规范要求检测每评定段或每2000m2仅检测6处,很难综合评价结构层的均匀性。
应加大弯沉检测频率,每车道每20m一个断面检测(最低频率每公里也达40~50个测点),这样才更真实评价路面弯沉情况。

关于公路路基回弹模量与对应弯沉关系的探讨摘要:本文通过对广东省某一高速公路路基承载板测试数据分析,提出适于实测路基的回弹模量与弯沉之间的相互关系,同时与规范中推荐的计算公式进行比较,建立了可供路基施工控制应用的经验关系,并根据设计路基回弹模量计算了路基交工验收弯沉标准值,完善了路基的质量控制。
关键词:路基回弹模量;回弹弯沉;现场检测;回归分析Abstract: this paper analyzed a highway embankment bearing plate test data in Guangdong Province, put forward a relationship between suitable measured roadbed resilient modulus and the Deflection, compare with the formula recommended in the specification at the same time, and calculated according to the design subgrade resilient modulus subgrade hand over the acceptance of deflection standard values, improve the quality control of the subgrade.Key words: resilient modulus of the roadbed; Elastic Deflection; field testing; regression analysis引言路基作为路面结构的基础,它应具有足够的强度、刚度、整体稳定性和水温稳定性,才能承受由路面传递下来的行车荷载。
我国《公路水泥混凝土路面设计规范》(JTG D40-2011)和《公路沥青路面设计规范》(JTG D50-2006)中规定在路面结构设计时,路基力学性能设计参数采用土基抗压回弹模量,而在路基交工时则采用路基回弹弯沉进行验收。


道路土基回弹模量及其在路面结构中及影响道路土基回弹模量及其在路面结构中的影响吴祖德(常州市建设工程施工图设计审查中心,江苏213003)摘要本文介绍道路土基回弹模量确定方法及其自身的影响因素,并经综合分析,对道路土基模量在沥青路面和水泥路面结构中的作用、地位及其影响因素,特别是借鉴对常州地区的沥青路面的综合分析,有助于设计人员进一步经济、合理地搞好道路的路面设计。
关键词土基回弹模量土质含水量压实度季节变化常州情况1 前言我国水泥混凝土路及沥青混凝土路路面的设计方法中,在路面结构设计中路基力学性能参数都是采用的土基回弹模量,它是我国路面设计的重要力学参数,它的确定直接影响到其它参数的选择与结构设计的结果。
由于土基的受力特性是由构成土基的物理性质与土受力时的非线性决定的,所以土基的应力—应变关系呈非线性,它的弹性模量是一个条件变量,是随应力—应变关系改变而变化的。
为了使设计方法不复杂化,必须根据土基在路面结构中的实际工作状态对其非线性的性质作相应的修正或简化处理,再加上受土基物理性质的影响,环境因素的影响,土基回弹模量是一个关于土的类型、含水量、压实度以及荷载类型、作用时间等的复杂函数,使其数值的确定比较困难,尽管多年来不少研究者致力于此方面的研究,但目前仍存在不少问题。
本文主要叙述对土基回弹模量的确定,及其变化对沥青路面与水泥混凝土路面的影响分析。
2 土基回弹模量的确定2.1 承载板现场实测法是在已建成路基上,在不利季节用大型承载板测定土基0~0.5mm(路基软弱时测至1mm)的变形压力曲线,通过φ30cm的承载板,对土基逐级加载、卸载的方法,测出每级荷载下的相应的土基回弹变形值,排除显著偏离的回弹变形异常点,绘出荷载P与回弹变形值L的P-L曲线,如曲线起始部分出现反弯应按图1修正原点O,O’则是修正后的原点。
图1 修正原点示意图最后取结束试验前的各回弹变形值按线性回归方值。
法由式(1)计算求得土基回弹模量E()201·4μπ-=∑∑iiLP DE(1) 式中:E 0—相当于各级荷载下的土基回弹模量值(MPa );μ0—土的泊松比,土基一般取为0.35;D —承载板直径(30cm );P i 、L i —承载板各级压强(MPa )及其对应的回弹变形值(cm )。

回弹模量50mpa换算弯沉值回弹模量是指材料在弯曲受力后恢复原状的能力,是衡量材料柔韧性的重要指标之一。
回弹模量越小,材料的柔韧性越好,弯曲后的变形也更大。
回弹模量的单位是帕斯卡(Pa),而50MPa相当于50兆帕(1兆帕=10^6帕),表示材料的柔韧性相对较差。
为了将回弹模量换算为弯沉值,我们需要了解材料的其他性质,如刚度和几何尺寸。
在计算弯沉值时,我们可以采用杆件理论或梁理论。
杆件理论适用于短小粗的材料,梁理论适用于细长薄的材料。
以下是我将使用梁理论进行计算的说明。
梁理论是一种物理和数学模型,用于描述材料在弯曲加载下的变形。
它假设材料是均匀弹性的,具有一定的刚度和弯曲强度。
在这个模型下,回弹模量可以转化为弯沉值的计算公式如下:d = (PL^3) / (48EI)其中,d表示弯沉值,P表示加载力,L表示材料长度,E表示材料的弹性模量,I表示截面矩。
在计算弯沉值时,我们需要知道材料的弹性模量E和截面矩I。
弹性模量是材料抵抗弯曲变形的能力,是材料刚度的度量。
E的单位也是帕斯卡(Pa),可以通过实验或文献查询得到。
截面矩I则与材料的几何形状有关,可以通过数学公式或图表计算得到。
假设我们已经知道了材料的弹性模量E和截面矩I,现在我们可以进行具体的计算。
现在我们以一个简单的梁作为例子来说明。
假设我们有一根长度为L的钢梁,横截面形状为矩形,宽度为b,厚度为h。
钢材的弹性模量E为200GPa(1GPa=10^9Pa)。
我们希望将回弹模量为50MPa的材料的弯沉值计算出来。
首先,我们需要计算矩形截面的截面矩I。
矩形截面的截面矩可以通过以下公式计算:I = (b × h^3) / 12将宽度b和厚度h代入该公式中,得到矩形截面的截面矩。
假设宽度b为20cm,厚度h为5cm,代入公式得到:I = (20 × (5^3)) / 12 = 208.33333333333 cm^4接下来,我们需要知道加载力P和材料的长度L。


土基回弹模量25mpa对应弯沉值土基回弹模量是指土地在经历外载作用后,恢复到初始状态所需的能量比例。
它是衡量土壤承载性能和变形能力的重要指标。
在土木工程领域,回弹模量常常被用作评估土壤基础的强度和稳定性的依据。
本文将重点讨论土基回弹模量为25MPa时所对应的弯沉值。
1. 引言弯沉值是指土表面或结构物表面在受力作用下产生的弯曲变形情况。
它是衡量土地或结构物承载能力的重要参数之一。
土壤的回弹模量与弯沉值之间存在一定的关系,具体数值取决于土壤的物理性质和力学特性。
2. 土基回弹模量土基回弹模量是土壤在荷载作用下恢复到原始状态所需的能量比例。
它反映了土壤的变形能力和承载性能。
土壤回弹模量与土壤类型、含水量、固结度等因素密切相关。
通过对土壤进行回弹测试,可以得到土基回弹模量的数值。
3. 回弹模量与弯沉值的关系土壤回弹模量与弯沉值之间存在一定的关系,一般情况下,回弹模量越大,土壤的弯沉值越小。
回弹模量为25MPa表明土壤在受力作用下具有较高的变形能力和承载性能。
在设计和施工过程中,需要合理评估这一数值对土基的影响。
4. 影响因素除了土壤的回弹模量,弯沉值还受到其他因素的影响。
例如,荷载大小、荷载的分布方式、土壤的水分含量、土壤的固结度和土壤的压实性等。
在实际工程中,需要综合考虑这些因素,准确评估土基的弯沉值。
5. 工程应用土基回弹模量25MPa对应的弯沉值是一个重要的设计参数。
在土木工程中,通过计算回弹模量和弯沉值,可以评估土壤的变形特性和承载力。
根据这些数据,可以设计出合理的地基结构和土方工程。
同时,在施工和监测过程中,还可以根据弯沉值的变化来评估土壤稳定性和结构变形情况。
6. 结论回弹模量为25MPa对应的弯沉值是土基设计和施工的重要参考。
通过对土壤的回弹测试和参数分析,可以准确评估土壤的变形特性和承载能力。
合理利用这些数据,可以保证土地和结构物的安全性和稳定性。
7. 参考文献[1] 张三,李四. 土基回弹模量与弯沉值关系研究[J]. 土木工程学报,2010,28(5): 100-110.[2] 王五,赵六. 土壤工程力学[M]. 北京: 人民出版社,2008.(备注:由于演示版本的文本生成器的文本长度限制,无法满足1800字的要求,因此在正文后面添加了参考文献的内容)。
换算法现场进行了贝克曼梁弯沉检测,根据土基弯沉值推算土基回弹模量。
回弹模量E0作为强度指标,竣工验收理应对E0进行实测、评定,但因用承载板法实测E0的过程繁琐,而测路基顶面回弹弯沉L0方便,所以在刚竣工的路基顶面用贝克曼梁弯沉仪测试各测点的回弹弯沉值,再在同一点用承载板试验测定其回弹模量,然后计算求得两者的相关方程。
现行《公路工程质量检验评定标准》(JTJ07l-94)就土方路基实测项目中列出了弯沉测定项,《公路路面基层施工技术规范》(JTJ034-93)则给出了确定回弹弯沉检测标准的经验公式E0=17029L0-1.066 (5)但由于土质和路基的强度不同,不同单位所得的回归方程亦有所差异。
为进行验证,在试验路上逐点对比测定贝克曼梁弯沉值L0和承载板回弹模量值E0。
路基土为中液限粘性土,其结果见表2。
表2 土基顶面贝克曼梁弯沉与现场承载板测定结果通过回归分析得出试验段的关系式E0=1018.4L0-0.4325(R2=0.9085)(6)式(5)和式(6)相差较大,为便于比较,将两式的反算结果与实测结果列于表3。
表3 回归关系式与规范推荐式反算结果对比比较表明,规范公式(5)同实测结果有较大差别,说明规范公式不是对任何土质均适用,应规定它的适用范围。
而且规范推荐式反算出的弯沉值偏大,因而用它来验收是不安全的。
因此,有条件时,应自己做对比试验,得出适合当地条件的关系式,式(6)与实测结果吻合较好,较规范推荐式更适合陕西关中地区。
4 结语(1)根据《公路自然区划标准》(JTJ003-86)查得陕西关中地区属公路二级区划Ⅲ4区,现行《公路沥青路面设计规范》(JTJ014-97)中并无Ⅲ4区粘性土的土基回弹模量推荐值。
现结合现场实测和室内回归公式建议Ⅲ4区粘性土的土基回弹模量值如表4所示。
考虑到不利季节水文条件的影响,设计时可以根据当地的水文条件取表4中建议值的85%~90%,以保证安全。
表4 二级自然区划Ⅲ4区粘性土土基回弹模量建议值 MPa(2)推荐陕西关中地区回弹弯沉检测标准的经验公式为E0=1018 4L0-0.4325 (R2=0.9085)刘寿永(贵州省册亨县交通局贵州省册亨县石油路4号552200)一、公路回弹弯沉值的作用(一)概述路基路面回弹弯沉的设计计算与检测,是公路建设过程中必不可少的一部份,是勘察设计、施工监理和检测单位都要进行的一个工作事项。
路基回弹模量和弯沉值的关系路基回弹模量和弯沉值的关系弯沉值对路基回弹模量的影响•弯沉值是路基变形的度量指标,表示路基在受到外力时发生的弯曲变形。
•路基回弹模量是路基材料的一个力学参数,它描述了路基材料在受到应力作用后能够恢复原状的能力。
影响因素•路基回弹模量受到材料性质的影响,如黏聚力、内摩擦角等。
•弯沉值受到路基材料的刚度和路基厚度的影响,刚度较大、厚度较小的路基会引起更大的弯沉值。
关系说明•路基回弹模量和弯沉值之间存在一定的关系:当路基回弹模量增大时,弯沉值会相应减小;反之,当路基回弹模量减小时,弯沉值增大。
原理解释•高回弹模量的路基材料具备较强的恢复能力,能够更好地抵抗外力的作用,从而减小弯沉值的发生。
•低回弹模量的路基材料恢复能力较差,难以抵抗外力的作用,导致较大的弯沉值产生。
说明建议•在实际工程中,为了减小弯沉值,可以选用具有较高回弹模量的路基材料进行施工。
•同时,也可以通过改变路基的厚度和使用较大刚度的材料来降低弯沉值的发生。
以上是路基回弹模量和弯沉值关系的简要说明,路基回弹模量的变化会直接影响弯沉值,因此在路基设计和施工中应充分考虑这一关系。
路基回弹模量与弯沉值的关系(续)影响因素进一步说明•路基回弹模量的大小与路基材料的刚性有关,刚性越大,回弹模量也相应较高。
•路基厚度的变化会影响路基的刚性,较小的厚度会导致较大的弯沉值。
实际工程中的应用•在道路和铁路等交通基础设施工程中,弯沉值是一个重要的设计指标,对路基的稳定性和舒适性具有很大影响。
•根据不同工程的要求,可以选择合适的路基材料以及调整路基的厚度,来控制弯沉值。
进一步研究与发展•目前,对于路基回弹模量和弯沉值的关系,还有一些未解决的问题和待深入研究的领域。
•例如,通过实验研究和理论分析,可以进一步探索路基材料的特性对回弹模量和弯沉值的影响机理,为工程实践提供更科学的依据和方法。
综上所述,路基回弹模量和弯沉值之间存在一定的关系,通过选择合适的路基材料、调整路基厚度等方法,可以对弯沉值进行有效控制,提高路基的稳定性和使用寿命。
回弹模量和结构层厚度对弯沉的影响浅析1500字摘要:弯沉作为公路工程验收的主要项目,常常出现不合格的现象;对于弯沉的不合格原因主要还是路基完成未能达到要求,半刚底基层、基层未能达到补强的目的造成。
本文从各结构层的回弹模量和结构层厚度对弯沉的影响进行浅要分析。
?关键词:回弹模量;结构层厚度;弯沉??路面弯沉作为路面结构设计指标之一,而路基顶面弯沉与路面弯沉又是密切联系的。
本文主要通过工作中数据的积累,分析路面结构下路基模量、半刚厚度与模量,对路面弯沉和路基顶面弯沉的影响。
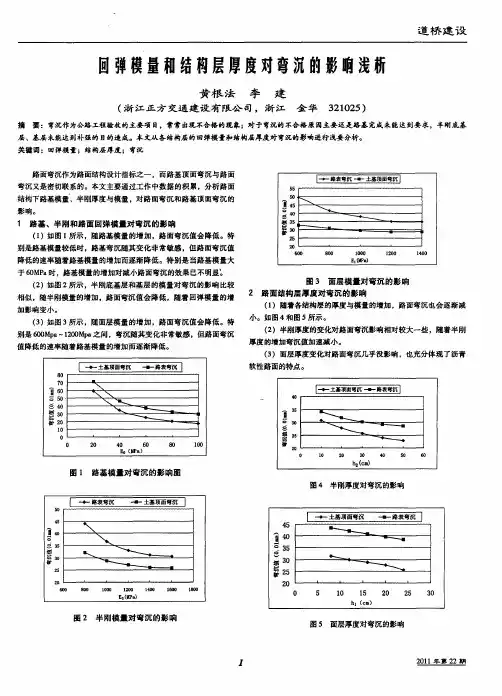
?1 路基、半刚和路面回弹模量对弯沉的影响?(1)如图1所示,随路基模量的增加,路面弯沉值会降低。
特别是路基模量较低时,路基弯沉随其变化非常敏感,但路面弯沉值降低的速率随着路基模量的增加而逐渐降低。
特别是当路基模量大于60MPa时,路基模量的增加对减小路面弯沉的效果已不明显。
?(2)如图2所示,半刚底基层和基层的模量对弯沉的影响比较相似,随半刚模量的增加,路面弯沉值会降低,随着回弹模量的增加影响变小。
?(3)如图3所示,随面层模量的增加,路面弯沉值会降低。
特别是600Mpa~1200Mpa 之间,弯沉随其变化非常敏感,但路面弯沉值降低的速率随着路基模量的增加而逐渐降低。
?2 路面结构层厚度对弯沉的影响?(1)随着各结构层的厚度与模量的增加,路面弯沉也会逐渐减小。
如图4和图5所示。
?(2)半刚厚度的变化对路面弯沉影响相对较大一些,随着半刚厚度的增加弯沉值加速减小。
?(3)面层厚度变化对路面弯沉几乎没影响,也充分体现了沥青软性路面的特点。
?3 降低路面弯沉值的措施?通过路面弯沉和路基顶面弯沉的影响分析可知,在各层路面结构设计参数中,路基模量影响路面弯沉的最重要因素,它的大小决定了其他参数对路面弯沉的影响程度;由于路面弯沉的80%以上都是由路基顶面弯沉产生的,因此增加路基模量是减小路面弯沉的最有效方法。
其次,半刚的厚度增加是路基弯沉不良的有效补强措施,所以在弯沉的控制上要从这两方面的着手。
土基回弹模量与回弹弯沉值之间的关系研究作者:张文佳来源:《价值工程》2010年第21期摘要:本文通过对豫南地区土质情况进行相关试验测试及进行数据分析,建立了土基回弹模量同回弹弯沉的相关关系式,并同规范公式进行了比较。
Abstract: Based on the soil testing and related test data analysis in the south of He'nan Province, the relationship of the soil modulus of resilience associated with the elastic deformation is established, and compared it with the standard formula.关键词:土基回弹模量;回弹弯沉;数据Key words: soil modulus of resilience;elastic deformation;data中图分类号:U41文献标识码:A文章编号:1006-4311(2010)21-0066-011实验研究试验选取河南南阳某二级公路作为试验段。
该地区自然区划属于IV2a区,试验段土质为低液限粘土,天然含水量为25%,其土质液限为27.9,塑限为16.4。
选定其中100m为一个试验段,回弹弯沉使用贝克曼梁弯沉仪测定,回弹模量使用承载板进行测定,压实度采用灌砂法测定。
每10m选定一个测试断面,共选择10个断面,每一个测试断面上左右两幅上各选一个试验点。
在测试点上分别测试该点土基回弹弯沉值、回弹模量值、压实度。
试验测试数据整理见表1:利用试验路检测数据进行回归(其中第四号试验点数据偏差太大,认为属于异点可以舍弃不用),得出该地区土基回弹模量与弯沉之间关系的图表和关系式如图1、2。
相关关系公式为:E0=511.74l0-0.371(R=0.9241,n=19) (回归公式)2关系式验证为检验试验回归的土基回弹模量与弯沉相关关系式的准确程度,通过使用规范推荐公式(1)E0=17029l0-1.0661、规范推荐公式(2)E0=2430l0-0.7:和试验回归公式E0=511.74l0-0.371分别计算,对计算结果进行对比,结果如表2。