当前位置：文档之家 › 3.1.2空间向量的共线与共面

3.1.2空间向量的共线与共面

  • 格式：ppt
  • 大小：614.02 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

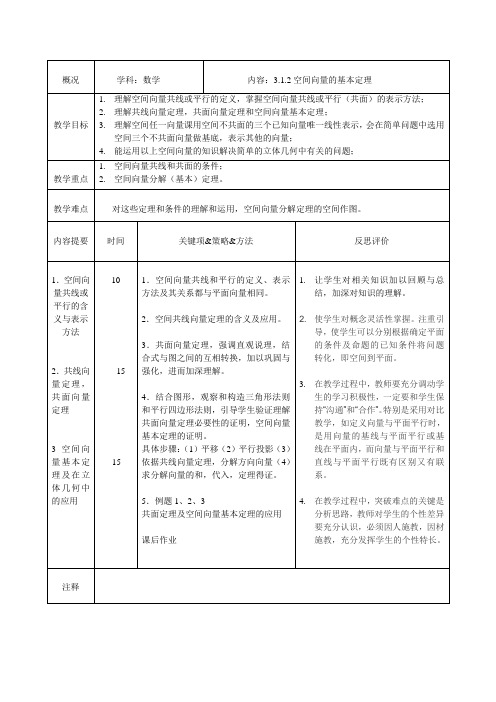
空间向量的基本定理3.1.2版块式教案

空间向量的基本定理3.1.2版块式教案

教学重点 教学难点
内容提要
时间
关键项&策略&方法
反思评价
1．空间向 量共线或 平行的含 义与表示 方法
10
1．空间向量共线和平行的定义、表示 方法及其关系都与平面向量相同。 2．空间共线向量定理的含义及应用。
1. 让学生对相关知识加以回顾与总 结，加深对知识的理解。
2．：数学
内容：3.1.2 空间向量的基本定理
教学目标
1. 理解空间向量共线或平行的定义，掌握空间向量共线或平行（共面）的表示方法； 2. 理解共线向量定理，共面向量定理和空间向量基本定理； 3. 理解空间任一向量课用空间不共面的三个已知向量唯一线性表示， 会在简单问题中选用 空间三个不共面向量做基底，表示其他的向量； 4. 能运用以上空间向量的知识解决简单的立体几何中有关的问题； 1. 空间向量共线和共面的条件； 2. 空间向量分解（基本）定理。 对这些定理和条件的理解和运用，空间向量分解定理的空间作图。
15
3 空间向 量基本定 理及在立 体几何中 的应用
15
2. 使学生对概念灵活性掌握。注重引 导，使学生可以分别根据确定平面 3．共面向量定理，强调直观说理，结 的条件及命题的已知条件将问题 合式与图之间的互相转换，加以巩固与 转化，即空间到平面。 强化，进而加深理解。 3. 在教学过程中，教师要充分调动学 4．结合图形，观察和构造三角形法则 生的学习积极性，一定要和学生保 和平行四边形法则，引导学生验证理解 持“沟通”和“合作”。 特别是采用对比 共面向量定理必要性的证明，空间向量 教学，如定义向量与平面平行时， 基本定理的证明。 是用向量的基线与平面平行或基 具体步骤： （1）平移（2）平行投影（3） 线在平面内，而向量与平面平行和 依据共线向量定理，分解方向向量（4） 直线与平面平行既有区别又有联 求分解向量的和，代入，定理得证。 系。 5．例题 1、2、3 共面定理及空间向量基本定理的应用 课后作业 4. 在教学过程中，突破难点的关键是 分析思路，教师对学生的个性差异 要充分认识，必须因人施教，因材 施教，充分发挥学生的个性特长。

原创1：3.1.2 空间向量的基本定理

原创1：3.1.2 空间向量的基本定理
(2)基底不同，对于向量的分解形式不同.
典例分析
若{a，b，Ԧc}是空间的一个基底，判断{a＋b，b＋Ԧc，Ԧc＋a}能否
作为该空间的一个基底．
是否共面
【解析】假设a＋b，b＋Ԧc，Ԧc＋a共面，
则存在实数λ，μ使得
a＋b＝λ(b＋Ԧc)＋μ(Ԧc＋a)，
∴ a＋b ＝μa＋λb＋(λ＋μ)Ԧc.
答案
②③
典例分析
空间四边形OABC中，M，N是△ABC，△OBC的重心，设＝a，
＝b， ＝Ԧc，用向量a，b，Ԧc表示向量， ， .
利用线性运算，结合图形，
【解析】如图，取BC中点P，
O
对向量进行分解
则A、M、P，O、N、P分别共线，
a
cԦ
连结AP，OP.
2
AM＝OA＋AM＝a＋ AP
＝ k ＝k( + )
跟踪训练
＝k( − + − )
＝ − + −
＝ + .
所以E、F、G、H共面．
(2) ＝ − ＝k( − )＝k ，
且由第(1)问的证明中知＝k，
于是EF∥AB，EG∥AC.且EF∩EG＝E，AB∩AC＝A，
已知平行四边形ABCD，从平面AC外一点O引向量
＝k， ＝k ， ＝k ， ＝k ＝k，
求证：(1)四点E、F、G、H共面；
(2)平面EG∥平面AC.
证明：(1)因为四边形ABCD是平行四边形，
所以 = + ，
= − ＝ k － k
第三章 空间向量与立体几何
§3.1.2
空间向量的基本定理
高中数学选修2-1·精品课件
引入课题

3.1.2共线与共面

3.1.2共线与共面
对空间任意一点O，存在实数对x、y，z，使
OP xOA yOB zOC （其中x+y+z=1）
作 业： 教辅第23页~第26页,活页课时作业十一
教材31页练习:
1. 空间四边形ABCD中,连结AC、BD， M、G分别是BC、CD边的中点,化简：
A
（） AB BC CD AD 1
A1
A2
A3 An
An1
A4
4. 平行六面体： 平行四边形ABCD(包括它的内部)平移向量 a到A1B1C1D1的轨迹所形成的几何体，叫做平行六面体.
D1 A1 a A B1 C1 A1 D A B
D1
B1
C1
D
B
C
C
AB AD AA1 AC1
记作ABCD—A1B1C1D1，它的六个面都是平行四边 形，每个面的边叫做平行六面体的棱.
于是点 P在平面MAB内，向量p // 平面MAB .
即向量 p 与 a 、 共面 . b
(3)共面向量定理: 如果两个向量a、b 不共线，则向量p与 向量a、b共面的充 要条件是存在实数 对x、y，使 B b p A A'
P
M
a
p = xa + yb.
ห้องสมุดไป่ตู้.O
推论:空间一点P 位于平面MAB内的充分必要条件是存在 有序实数对x、y，使 MP = xMA + yMB 或对空间任一定点O，有 OP = OM + xMA + yMB. 即 OP (1 x y )OM xOA yOB （平面MAB的向量表达式）
证明：( 2) EF OF OE
k (OB OA)
k AB

3.1.2空间向量共面定理

3.1.2空间向量共面定理

3.1.2空间向量共面定理教学目标：1．理解共线向量定理和共面向量定理及它们的推论；2．掌握空间直线、空间平面的向量参数方程和线段中点的向量公式．教学重、难点：共线、共面定理及其应用． 教学过程： （一）复习：1．空间向量的概念及表示:(二)阅读课本P 74～P 75，⑴怎样的向量叫做共线，共面向量？⑵两个向量共线，共面的充要条件是什么？1．共线（平行）向量：2．共线向量定理：推论：问题思考3．向量与平面平行：4．共面向量定理：如何证明？推论：()()1=020?a λ≠当实数时，表示什么意思？充要条件中，为什么规定（三）预习练习1、下列说法正确的是：A.在平面内共线的向量在空间不一定共线B.在空间共线的向量在平面内不一定共线C.在平面内共线的向量在空间一定不共线D.在空间共线的向量在平面内一定共线E.在平面内,任意两个向量一定共线2已知A 、B 、M 三点不共线，对于平面ABM 外的任一点O ，确定在下列各条件下，点P 是否与A 、B 、M 一定共面？3下列命题中正确的有______4.对于空间中的三个向量 它们一定是： A.共面向量 B.共线向量 C.不共面向量 D.既不共线又不共面向量5.已知点M 在平面ABC 内，并且对空间任意一点O ， ,则x的值为:_____（四）典型例题例1、已知A 、B 、P 三点共线，O 为空间任意一点，且 ，求 的值.αβ=+OP OA OBαβ+(1)3=＋－OB OM OP OA (2)4=--OP OA OB OM(1)=+⇒　与、共面;p xa yb p a b (2)⇒=+与、共面　；p a b p xa yb (3)=+⇒、、、共面；MP xMA yMB P M A B (4)⇒=+、、、共面；P M A B MP xMA yMB 2、、－MA MB MA MB=11＋＋33OM xOA OB OC (1)λλ=≠-AP PB变式、设点P 在直线AB 上并且 ，O 为空间任意一点， 求证：方法一：方法二：11111111,,,1,,,ABCD AC O OA kOA OB kOB OC kOC OD kODA B C D ====11变式：如图平行四边形，从平面外一点引向量求证：（）四点共面 (2)A C ||平面D'B'C'D ABC1λλ+=+OA OBOP 1,11,,,33ABCD ADEF M N BD AE BM BD AN AE MN CED ==例、如图，已知矩形与所在平面相互垂直，点分别在对角线上，且求证：平面五：课堂小结六，课后作业 P761,2,3强化训练：1.若对任意一点O ， ，则x+y=1是P 、A 、B 三点共线的： ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2．已知两个非零向量21,e e 不共线，如果21AB e e =+，2128AC e e =+，2133AD e e =-，求证：,,,A B C D 共面．3．已知324,(1)82a m n p b x m n yp =--=+++，0a ≠，若//a b ，求实数,x y 的值。

课件1：3.1.2 空间向量的数乘运算（共线与共面向量）

课件1：3.1.2 空间向量的数乘运算（共线与共面向量）

∴EH ∥FG且|EH |＝43|FG |≠|FG |.
又 F 不在直线 EH 上， ∴四边形 EFGH 是梯形．
规律方法 判断向量 a，b 共线的方法有两种： (1)定义法 即证明 a，b 所在基线平行或重合． (2)利用“a＝xb⇒a∥b”判断 a，b 是空间图形中的有向线段，利用空间向量的运算性质， 结合具体图形，化简得出 a＝xb，从而得 a∥b，即 a 与 b 共 线．
存在有序实数组{x，y，z}，使得 p＝ xa＋yb＋zc
.
其中，表达式 xa＋yb＋zc 叫做向量 a，b，c 的线性表
达式或线性组合， a，b，c 叫做空间的一个基底，记 作 {a，b，c} ，a，b，c 都叫做基向量.
互动探究
题型一：共线向量的判定 例 1 如图 3－1－11 所示，已知四边形 ABCD 是空间四边形，E，H 分别是边 AB，AD 的中点，F， G 分别是边 CB，CD 上的点，且C→F＝23C→B，C→G＝23C→D. 求证：四边形 EFGH 是梯形．
图 3－1－11
【思路探究】 (1)E→H与F→G共线吗？怎样证明？ (2)|E→H|与|F→G|相等吗？ 【自主解答】 ∵E，H 分别是 AB、AD 的中点， ∴A→E＝21A→B，A→H＝12A→D， 则E→H＝A→H－A→E＝12A→D－12A→B＝12B→D ＝21(C→D－C→B)＝12(32C→G－32C→F) ＝43(C→G－C→F)＝34F→G，
(2)由(1)知向量M→A，M→B，M→C共面，三个向量的基线又 过同一点 M，
∴M、A、B、C 四点共面， ∴M 在面 ABC 内．
规律方法 1．空间一点 P 位于平面 MAB 内的充分必要条件是存在有序 实数对(x，y)，使 MP xMA yMB.满足这个关系式的点 P 都 在平面 MAB 内；反之，平面 MAB 内的任一点 P 都满足这个 关系式．这个充要条件常用于证明四点共面．

空间向量基本定理

空间向量基本定理
3.1.2空间向量基本定理
回顾复习
一、共线向量： 1.共线向量:
如果表示空间向量的有向线段所在的直线互相平行或重合，
则这些向量叫做共线向量或平行向量．
r
r
r a
平行于
r b
记作
r a
//
r b
．
规定: o 与任一向量 a 是共线向量.
rrr r
2、共线向量定理 对空间任意两个向量a,b(a 0),
ur r r
序实数对 ( x, y) 使 p xa yb .
r b
C
ur p
P
请证明
A
r a
B
思考2：有平面ABC， 若P点在此面内，须 满足什么条件？
ur
rC
p
br Aa
B
P
O
结论:空间一点P位于平面ABC内
uuur uuur uuur
1.存在唯一有序实数对x,y使 AP x AB y AC
uuuur uuuur uuuur (4) P、M、A、B共面 MP xMA yMB ；
A.1个 B.2个 C.3个 D.4个
ur ur
2.
已知uue1ur, e2
是平面内两个不共线的向量,
ur uur uuur ur uur
uuur
ur
uur
若AB e1 e2 , AC 2e1 8e2 , AD 3e1 3e2 ,
uuur OP
2
uuur OA1来自uuur OB2
uuur OC
;
555
uuur uuur uuur uuur
(2) OP 2OA 2OB OC ；
uuur r uuur r
例1.如图三棱柱,设AB a, AC b, A1

3.1.2空间向量


A
O
a
l
BP
注:非零向量 a 叫做 方向向量. 直线 l 的方向向量.
⑴∵ AP // a ,∴存在唯一实数 t ∈ R ,使 AP = t a . ∴ 点 P 在直线 l 上 唯一实数 t ∈ R, 使 AP = t a ①
⑵对于任意一点 O,有 AP = OP OA , 则点 P 在直线 l 上 唯一实数 t ∈ R, 使 OP = OA + t a ② ⑶点 B 在直线 l 上,且 AB = a
一平面内的任一向量 a , 存在唯一的一对实数 t1 , t 2 使
a = t1 e1 + t 2 e2 .
a
e2
M
C
e2
e1
O
a
N
e1
进行分解, 对向量 a 进行分解, OC = OM + ON = t 1 e 1 + t 2 e 2
12
类似地, 空间向量基本定理 向量基本定理: 类似地,有空间向量基本定理:
∴ OP OA = y (OB OA) + z (OC OA) ∴ AP = y AB + z AC B C 共面. ∴点 P 与 A , , 共面
10
试证明:对于不共线的三点 B C 试证明:对于不共线的三点 A, , 和平面 ABC 外的 一点 O ,空间一点 P 满足关系式 OP = xOA+ yOB + zOC ,则 充要条件是 点 P 在平面 ABC 内的充要条件是 x + y + z = 1 . 证明: 证明:⑴充分性
上一节,我们发现: 上一节,我们发现: 1.空间一 空间一点 1.空间一点 P 在直线 AB 上的充要条件是 ________________________________. 唯一实数 t ∈ R, 使 AP = t AB

第3章 3.1.2 共面向量定理


→ → ②若AB＝CD，则 A，B，C，D 四点共线；
③若a，b不共线，则空间任一向量p＝λa＋μb(λ，μ∈R). 解析 当a，b中有零向量时，①不正确；
→ → AB＝CD时，A，B，C，D 四点共面不一定共线，故②不正确；
由p，a，b共面的充要条件知，当p，a，b共面时才满足p＝ λa＋μb(λ，μ∈R)，故③不正确.
→ → 此为空间共面向量定理，其实质就是平面向量基本定理，MA，MB实质 就是平面 MAB 内平面向量的一组基底.
D四点共面.
[思考辨析
判断正误] ) )
1.实数与向量之间可进行加法、减法运算 × .( 2.空间中任意三个向量一定是共面向量.( ×
→ → → 3.若 P，M，A，B 共面，则MP＝xMA＋yMB.( × )
题型探究
类型一 向量共面的判 定 例1 给出以下命题： ①用分别在两条异面直线上的两条有向线段表示两个向量，则 这两个向量一定不共面； ②已知空间四边形ABCD，则由四条线段AB，BC，CD，DA分
要条件是 存在有序实数组(x，y)，使得p＝xa＋yb
_____________________________________，即向量p可以由 两个不共线的向量a，b线性表示.
知识点三 空间四点共面的 条件
若空间任意无三点共线的四点，对于空间任一点 O，存在实数 x，y，z 使 → → → → 得OA＝xOB＋yOC＋zOD，且 x，y，z 满足 x＋y＋z＝1，则 A，B，C，
解答
反思与感悟
利用向量法证明向量共面问题，关键是熟练的
进行向量的表示，恰当应用向量共面的充要条件，解题过程 中注意区分向量所在的直线的位置关系与向量的位置关系.
跟踪训练 2 如图，在正方体 ABCD－A1B1C1D1 中，E，F 分别为 BB1 ― → ― → → 和 A1D1 的中点.证明：向量 A1B ， B1C ，EF是共面向量.

3.1.2空间向量的共线与共面


例. 如图，已知平行四边形ABCD，过平面AC外
一点O作射线OA，OB，OC，OD，在四条射线上
分别取点E，F，G，H，并且使
OE OF OG OH k, OA OB OC OD
O
求证： E，F，G，H四点共面.
DC
A
ห้องสมุดไป่ตู้
B
H
G
E
F
C
p
P
b
A aB
对空间任一点O,有OP OA xAB y AC ③
C
p
P
b
A aB
O 填空：OP (1__-_x_-_y)OA (_x___)OB (__y__)OC
③式称为空间平面ABC的向量表示式，空间中任意 平面由空 间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
P与A,B,C共面
AP xAB yAC
OP OA xAB y AC
OP xOA yOB zOC 0(x y z 1)
练习2.若对任一点O和不共线的三点A、B、C，
且有 OP xOA yOB zOC(x, y, z R), 则x+y+z=1 是四点P、A、B、C共面的（ C ）
A.必要不充分条件 C.充要条件
B
b
O
a 结论：空间任意两个向量都可平移到同 一个平面内，成为同一平面内的向量. 因此凡是涉及空间任意两个向量的问题， 平面向量中有关结论仍适用于它们.
1、共线向量:如果表示空间向量的有向
线段所在直线互相平行或重合,则这些向量
叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
思考:空间向量的平行满足传递性吗?
2.共线向量定理:对空间任意两个向量 a,b(b 0), a // b的充要条件是存在实数 使

空间向量的共线与共面


→
OP＝13
→→
2
OA＋βOB，则 β＝____3____.
二、共面向量:
1.共面向量:平行于同一平面的向量,叫
做共面向量.
b
d
c
a
注意：空间任意两个向量是共面的，但空间 任意三个向量 既可能共面，也可能不共面
那么什么情况下三个向量共面呢？
e e a
2 e1
由平面向量基本定理知，如果 e1， 2 是对只平于有面这一内一对的平实两面数个内1不的，共任2 ，线意使的 向向 量a 量a，1e，1那有么且2e2
分别取点E，F，G，H，并且使
OE OF OG OH k, OA OB OC OD
O
求证： E，F，G，H四点共面.
DC
A
B
H
G
E
F
B.充分不必要条件 D.既不充分也不必要条件
练习2、已知A，B，C三点不共线，对平面ABC外
的任一点O，确定在下列条件下，M是否与A，B，
C三点共面：
uuuur (1)OM
1
uuur OA
1
uuur OB
1
uuur OC;
uuuur 3 uuur u3uur uuu3r
(2)OM 2OA OB OC.
p xa yb在a，b确定的平面内,即p与a，b共面
a 2.共面向量定理：如果两个向量 ，b 不共线， a 则向量 p与向量 ， 共b面的充要条件是
存在实数对x,y使 p x yb
推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x,y使 AP xAB y AC
rC
ur p
P
br
其中向量 a叫做直线 的l 方向向量.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

其中向量 a 叫做直线 的l 方向向量.
P
a
空间直线的向量表示式
B A
O
三点共线的证明
A、B、P三点共线
P
AP t AB
OPOAtAB O
O PxO A yO(x B y1 )
特例: 若P为A,B中点,
则 OP1 OAOB 2
a
B A
练习 1
已知 A，B，P 三点共线，O 为空间任意一点，
并且此平行四边 a， b确 形定 在的平面内
pxayb在 a， b确定的,平 即 p与 面 a， b共 内面
a 2.共面向量定理：如果两个向量 ，b 不共线， a 则向量 p与向量 ， 共b面的充要条件是
存在实数对x,y使 p x yb
推论:空间一点P位于平面ABC内的充要条件是存在有
例. 如图，已知平行四边形ABCD，过平面AC外
一点O作射线OA，OB，OC，OD，在四条射线上
分别取点E，F，G，H，并且使
OE OF OG OH k,
OA OB OC OD
O
求证： E，F，G，H四点共面.
DC
A
B
H
G
E
F
A.必要不充分条件 C.充要条件
B.充分不必要条件 D.既不充分也不必要条件
练习2、已知A，B，C三点不共线，对平面ABC外 的任一点O，确定在下列条件下，M是否与A，B， C三点共面：
(1)OM1OA1OB1OC; 333
(2)OM2OAOBOC.
3.已知点M在平面ABC内，并且对空间任意一点
O(A ，O )1 MxOA (B ＋ )1 3 0OB＋ 1 3(O C C )3, 则x的(D 值)为1( ) 3
练习4.对于空间任意一点O，下列命题正确的是：A
(A)若 O P O A tA B，则P、A、B共线
(B)若 3 O PO A A B，则P是AB的中点
(C)若 O P O A tA B，则P、A、B不共线 (D)若 O P O A A B，则P、A、B共线
序实数对x,y使 APxAByAC
bC
p
P
A aB
对空间任一点O,有OP OA xAByAC ③
C
p
P
b
A aB
O 填空：O P (1_ -x-_yO _ _ A (x__ )O _ B (__y)_O _C _
③式称为空间平面ABC的向量表示式，空间中任意 平面由空 间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
P与A,B,C共面
APxAByAC
OP OA xAByAC
O x O P y O A z O B 0 ( x C y z 1 )
练习2.若对任一点O和不共线的三点A、B、C，
且有 O x P O y A O z B O (x ,C y ,z R )则,x+y+z=1 是四点P、A、B、C共面的（ C ）
3.1.2 空间向量的共线与共面
B
b
O
a 结论：空间任意两个向量都可平移到同 一个平面内，成为同一平面内的向量. 因此凡是涉及空间任意两个向量的问题， 平面向量中有关结论仍适用于它们.
1、共线向量:如果表示空间向量的有向
线段所在直线互相平行或重合,则这些向量
叫做共线向量(或平行向量),记作 a // b
如果空间向量
p
与两不共线向量 a ，b
共
面，那么可将三个向量平移到同一平面 ，则
有 p x yb

反果过p来，x对空y间b，任那意么两向个量不p共与线向的量向a量,
a ，b ，如
b 有什么位
Байду номын сангаас
置关系？
C
p
P
b
A aB
xa, yb分别与 a， b共线
xa, yb都在a，b确定的平面内
零向量与任意向量共线.
思考:空间向量的平行满足传递性吗?
2.共线向量定理:对空间任意两个向量 a,b(b0),a//b的充要条件是存在实数 使
a b
由此可判断空间中两直线平行或三点共线问题
推论:如果 l为经过已知点A且平行已知非零
向量 a 的直线,那么对任一点O,点P在直线 上l 的
充要条件是存在实数t,满足等式 O PO Ata
→
OP＝13
→→
2
OA＋βOB，则 β＝____3____.
二、共面向量:
1.共面向量:平行于同一平面的向量,叫
做共面向量.
b
d
c
a
注意：空间任意两个向量是共面的，但空间 任意三个向量 既可能共面，也可能不共面
那么什么情况下三个向量共面呢？

e
e
a
2
e1
由平面向量基本定理知，如果 e1， 2 是对只平于有面这一内一对的平实两面数个内1不的，共任2 ，线意使的 向a 向 量量a，1e，1那 有么且2e2