上海交大材基-第五章塑性变形与回复再结晶--复习提纲.
- 格式:doc
- 大小:295.51 KB
- 文档页数:10

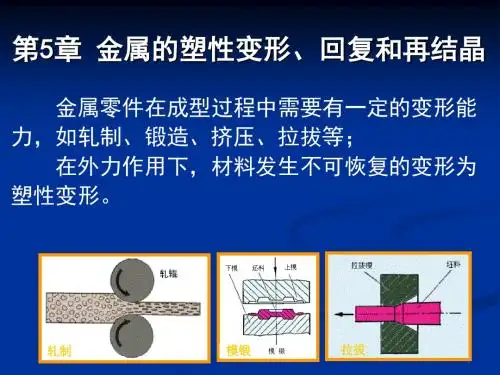
材料科学基础_第五章材料的形变和再结晶材料的形变是指材料在外力作用下发生的形状、尺寸及结构的变化。
形变可以分为弹性变形和塑性变形两种形式。
弹性变形是指物质在外力作用下只发生形状的改变,而不发生组织内部结构的改变,当外力消失时,物质能恢复到原来的形状。
塑性变形是指物质在外力作用下发生形状和内部结构的改变,当外力消失时,物质不能恢复到原来的形状。
形变过程中,材料的内部晶粒会发生滑移、动晶界和晶界迁移等变化,这些变化有助于减小材料中的位错密度,同时也能影响晶粒的尺寸、形状和分布。
当形变达到一定程度时,晶粒内部会产生高密度的位错,这会导致晶体的韧性下降,同时也容易引起晶粒的断裂和开裂。
因此,形变过程中产生的位错对材料的性能具有重要影响。
再结晶是指在材料的形变过程中,通过退火处理使晶粒重新长大,去除或减小形变过程中产生的位错和晶界等缺陷,从而改善材料的力学性能和其他性能。
再结晶的发生与材料的种类、成分、形变方式等因素有关。
再结晶可以通过两种方式实现:显微再结晶和亚显微再结晶。
显微再结晶是指晶粒在正常晶界上长大,形成新的晶粒;亚显微再结晶是指材料中的一些晶粒发生部分再结晶,形成较大的再结晶晶粒。
再结晶的发生和发展受到晶粒的尺寸、形状和分布的影响。
晶粒尺寸越小,再结晶发生越容易,且再结晶晶粒的尺寸也越小。
再结晶晶粒的尺寸和分布对材料的性能影响很大。
晶粒尺寸较小的材料通常具有优良的力学性能和高韧性,且易于加工。
因此,控制再结晶晶粒的尺寸和分布对材料的性能优化和加工有重要意义。
总之,材料的形变和再结晶是材料科学中重要的研究领域。
通过研究形变和再结晶的机制和规律,可以优化材料的性能和加工过程,从而推动材料科学的发展和应用。


1 单晶体的塑性变形铜单晶(a=0.36nm )在[112]方向加拉伸应力,拉伸应力为2.5×105Pa ,此条件下:(1)取向因子最大的滑移系有哪几个?(2)计算其分切应力多大?解:(1) Cu 为F.C.C 结构,易滑移面为{1,1,1},滑移方向为〈1,1,0〉,可以分别求出[112]方向与这些滑移系之间的两个夹角,然后得到12个取向因子的值。
(这里省略了)通过上述计算得到具体的滑移系(1,-1,1)[0,1,1]和(-1,1,1)[1,0,1]为具有最大取向因子滑移系。
(2) 根据施密特法则(公式略),F=δcosAcosB=1.02*105 Pa何谓临界分切应力定律?哪些因素影响临界分切应力大小? 解:(略)沿密排六方单晶的[0001]方向分别加拉伸力和压缩力,说明在这两种情况下,形变的可能方式。
解:1)滑移:a -拉伸的时,当c/a>=1.633,不会产生滑移,当c/a<1.633有可能产生滑移,可产生滑移的是{1,1,-2,2}<1,1,-2,-3>;其他滑移面不能产生滑移;b -压缩的时候结果和拉伸一样;2)孪生:拉伸和压缩的时候都可能产生孪生变形;3)扭折:拉伸的时候一般不易扭折变形,压缩的时候可以产生扭折变形。
试指出单晶体的Cu 与α-Fe 中易滑移面的晶面与晶向,并分别求它们的滑移面间距,滑移方向上的原子间距及点阵阻力,已知泊松比为ν=0.3,G Cu =48300MPa ,G α-Fe =81600MPa. 解:体心Fe 具有多种类的滑移系,但是滑移方向均相同。
力=90.56MPa 。
铝单晶体拉伸时,其力轴为[001],一个滑移系的临界分切应力为0.79MN/m2,取向因子COS φCOSλ=0.41,试问有几个滑移系可同时产生滑移?开动其中一个滑移系至少要施加多大的拉应力?解:Al为F.C.C结构,其滑移系共有{1,1,1}4<1,1,0>3=12个。

第5章材料的形变和再结晶提纲5.1 弹性和粘弹性5.2 晶体的塑性变形(重点)5.3 回复和再结晶(重点)5.4 高聚物的塑性变形学习要求掌握材料的变形机制及特征,以及变形对材料组织结构、性能的影响;冷、热加工变形材料的回复和结晶过程。
1.材料的弹性变形本质、弹性的不完整性及黏弹性;2.单晶体塑性变形方式、特点及机制(滑移、孪生、扭折)3.多晶体、合金塑性变形的特点及其影响因素4.塑性变形对材料组织与性能的影响;5.材料塑性变形的回复、再结晶和晶粒长大过程;6.影响回复、再结晶和晶粒长大的诸多因素(包括变形程度、第二相粒子、工艺参数等)7、结晶动力学的形式理论(J-M-A方程)8、热加工变形下动态回复、再结晶的微观组织特点、对性能影响。
9重点内容1. 弹性变形的特征,虎克定律(公式),弹性模量和切变弹性模量;材料在外力作用下发生变形。
当外力较小时,产生弹性变形。
弹性变形是可逆变形,卸载时,变形消失并恢复原状。
在弹性变形范围内,其应力与应变之间保持线性函数关系,即服从虎克(Hooke)定律:式中E为正弹性模量,G为切变模量。
它们之间存在如下关系:弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量。
2. 弹性的不完整性和粘弹性;理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等。
3. 滑移系,施密特法则(公式),滑移的临界分切应力;晶体中一个滑移面和该面上一个滑移方向组成。
fcc和bcc,bcc的滑移系?滑移系多少与塑性之间的关系。
滑移的临界分切应力:如何判断晶体中各个滑移系能不能开动?解释几何软化和几何硬化?为何多晶体塑性变形时要求至少有5个独立的滑移系进行滑移?4. 滑移的位错机制,派-纳力(公式);为什么晶体中滑移系为原子密度最大的面和方向?5. 比较塑性变形两种基本形式:滑移与孪生的异同特点;6. 多晶体塑性变形的特点:晶粒取向的影响,晶界的影响; 会判断多个晶体中哪些晶体会优先发生塑性变形?7. 细晶强化与Hall-Petch 公式, 高温晶界弱化的原因;晶粒细化为何能同时提高材料的强韧性?位错塞积群效应(应力集中区的应力数值等于外加切应力n可启动临近晶粒滑移,故 高温合金为何要采用定向凝固技术获得单晶?晶界滑动机制和扩散性蠕变 8. 固溶强化,屈服现象(吕德斯带),上下屈服点的柯垂耳理论和一般位错增殖理论,应变时效;d c dcττ= 金属有四大著名的强化机制,请给出这几种机制的名称,物理实质,定量描述其强化效果的数学公式。


材料科学基础第五章材料的变形与再结晶材料的变形与再结晶是材料科学基础的重要课题之一,对于材料的使用性能和制备工艺有着重要的影响。
本文将从变形机制、再结晶机制以及变形与再结晶的关系等方面进行探讨。
材料的变形是指材料的形状、尺寸以及内部结构在受到外力作用下的改变。
变形可以分为弹性变形和塑性变形两类。
弹性变形是指材料在加载后可以恢复到原来的形状和尺寸,而塑性变形则是指材料在加载后不能恢复到原来的形状和尺寸。
材料的塑性变形主要是由于材料晶体结构中的位错导致的。
位错是指晶体中存在的局部的原子排列错误。
在加载时,外力作用在晶体上,使得晶体中的原子在位错的作用下发生滑移,从而导致整体的塑性变形。
再结晶是指材料在一定条件下,通过断裂和重结晶可以重新形成新的晶粒。
再结晶的机制主要是晶界和位错的动态行为。
晶界是指两个晶粒之间的界面,在塑性变形过程中,晶界可以通过重结晶来消除变形能量,从而保证材料的继续塑性变形。
变形和再结晶有着密切的关系。
塑性变形过程中,位错密度会不断增加,晶界也会发生移动和重新排列,从而改变了材料的晶粒形态和尺寸。
当位错密度达到一定程度时,晶界开始活动,晶粒开始长大,并且会形成新的晶粒,即再结晶发生。
再结晶可以消除塑性变形过程中的缺陷,并且通过晶界的活动实现晶粒尺寸的控制。
材料的变形与再结晶对材料的性能和制备工艺有着重要的影响。
塑性变形可以提高材料的强度和硬度,改善材料的力学性能。
再结晶可以改善材料的塑性变形能力,降低材料的应力集中和脆弱性,提高材料的韧性和延展性。
在材料制备过程中,变形和再结晶的控制对材料的组织和性能具有重要的意义。
合理的变形和再结晶工艺可以获得理想的材料微观结构,从而提高材料的使用性能。
总之,材料的变形与再结晶是材料科学基础中的重要内容。
通过对变形机制和再结晶机制的研究,可以了解材料的塑性变形和再结晶的机理,进而控制和调整材料的性能和组织。
这对于材料的应用和制备工艺都具有重要的意义。

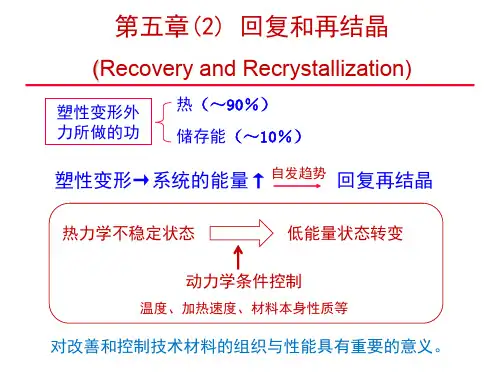


北京科技大学材料科学与工程专业814 材料科学基础主讲人:薛春阳第五章材料的形变和再结晶本章主要内容1.弹性和黏弹性2.晶体的塑性变形3.回复和再结晶4.热变形和动态回复、动态再结晶5.陶瓷形变的特点本章要求1.了解弹性和黏弹性的基本概念2.熟悉单晶体的塑性变形过程3.熟悉多晶体的塑性变形过程4.掌握塑性变形对材料组织和性能的影响5.掌握回复和再结晶的概念和过程6.熟悉动态回复和动态再结晶的概念和过程7.了解陶瓷变形的特点和一些基本概念应变应力b σsσe σbk s e ob εk ε变形的五个阶段:1.弹性变形2.不均匀的屈服变形3.均匀的塑性变形4.不均匀的塑性变形5.断裂阶段抗拉强度屈服强度弹性极限知识点1 弹性的不完整性定义:我们在考虑弹性变形的时候,通常只是考虑应力和应变的关系,而没有考虑时间的影响,即把物体看作是理想弹性体来处理。
但是,多数工程上应用的材料为多晶体甚至为非晶体,或者是两者皆有的物质,其内部存在着各种类型的缺陷,在弹性变形是,可能出现加载线与卸载线不重合、应变跟不上应力的变化等有别于理想弹性变形的特点的现象,我们称之为弹性的不完整性。
弹性不完整的现象主要包括包申格效应、弹性后效、弹性滞后、循环韧性等1.包申格效应材料预先加载才生少量的塑性变形(4%),而后同向加载则 升高,反向加载则 下降。
此现象称之为包申格效应。
它是多晶体金属材料的普遍现象。
2.弹性后效一些实际晶体中,在加载后者卸载时,应变不是瞬时达到其平衡值,而是通过一种弛豫过程来完成其变化的。
这种在弹性极限 范围内,应变滞后于外加应力,并和时间有关的现象,称之为弹性后效或者滞弹性。
3.弹性滞后由于应变落后与应力,在应力应变曲线上,使加载与卸载线不重合而是形成一段闭合回路,我们称之为弹性滞后。
弹性滞后表明,加载时消耗于材料的变形功大于卸载时材料恢复所释放的变形功,多余的部分被材料内部所消耗,称之为内耗,其大小用弹性滞后环的面积度量。
上海交通大学材料科学基础专业考试大纲一、专业科目与代码:827材料科学基础二、指定参考书《材料科学基础》(第3版)徐祖耀等上海交通大学出版社《材料科学基础辅导与习题》(第3版)蔡珣等上海交通大学出版社三、827材料科学基础考试大纲一、复习要求:要求考生掌握金属材料的结构、组织、性能方面的基本概念、基本原理;理解金属材料的结构、组织、性能之间的相互关系和基本变化规律。
二、主要复习内容:(一)晶体学基础理解晶体与非晶体、晶体结构与空间点阵的差异;掌握晶面指数和晶向指数的标注方法和画法;掌握立方晶系晶面与晶向平行或垂直的判断;掌握立方晶系晶面族和晶向族的展开;掌握面心立方、体心立方、密排六方晶胞中原子数、配位数、紧密系数的计算方法;掌握面心立方和密排六方的堆垛方式的描述及其它们之间的差异。
重点:晶体中原子结构的空间概念及其解析描述(晶面和晶向指数)。
(二)固体材料的结构掌握波尔理论和波动力学理论对原子核外电子的运动轨道的描述。
掌握波粒两相性的基本方程。
掌握离子键、共价键、金属键、分子键和氢键的结构差异。
了解结合键与电子分布的关系和键合作用力的来源。
掌握影响相结构的因素。
了解不同固溶体的结构差异。
重点:一些重要类型固体材料的结构特点及其与性能的关系。
三、晶体中的缺陷掌握缺陷的类型;掌握点缺陷存在的必然性;掌握点缺陷对晶体性能的影响及其应用。
理解位错的几何结构特点;掌握柏矢量的求法;掌握用位错的应变能进行位错运动趋势分析的方法。
掌握位错与溶质原子的交互作用,掌握位错与位错的交互作用。
掌握位错的运动形式。
掌握位错反应的判断;了解弗兰克不全位错和肖克莱不全位错的形成。
重点:位错的基本概念和基本性质。
四、固态中的扩散理解固体中的扩散现象及其与原子运动的关系,掌握扩散第一定律和第二定律适用的场合及其对相应的扩散过程进行分析的方法。
掌握几种重要的扩散机制适用的对象,了解柯肯达尔效应的意义。
掌握温度和晶体结构对扩散的影响。
第一章原子结构和键合(4学时)了解物质由原子组成,而组成材料的各元素的原子结构和原子间的键合是决定材料性能的重要因素。
§1 原子结构(一)、原子结构; (二)、原子间的键合; (三)、高分子链。
§2 原子间的键合(一)、金属键 (二)、离子键 (三)、共价键(四)、范德华力 (五)、氢键第二章固体结构(8学时)固态原子按其原子(或分子)聚集的状态,可划分为晶体与非晶体两大类。
晶体中的原子在空间呈有规则的周期性重复排列;而非晶体中的原子则是无规则排列的。
材料的性能与材料各元素的原子结构和键合密切相关,也与固态材料中原子或分子在空间的分布排列和运动规律以及原子集合体的形貌特征密切相关。
§1 晶体学基础(一)、晶体的空间点阵1.空间点阵概念2.晶胞3.晶系与布拉菲点阵4.晶体结构与空间点阵的关系(二)、晶向指数和晶面指数1.阵点坐标2.晶向指数3.晶面指数4.六方晶系指数5.晶带6.晶面间距§2 金属的晶体结构(一)、面心立方晶体结构的晶体学特征(fcc)(二)、体心立方晶体结构的晶体学特征(bcc)(三)、密排六方晶体结构的晶体学特征(hcp)§3 金属的相结构(一)、固溶体1.置换固溶体2.间隙固溶体3.有序固溶体4.固溶体的性质(二)、中间相1.正常价化合物2.电子化合物3.原子尺寸因素化合物(ⅰ)间隙相和间隙化合物§4 离子晶体结构(一)、NaCl型结构 (二)、萤石型结构 (三)、CsCl型结构 (四)、a-Al2O3型结构§5 共价晶体结构(一)、金刚石结构 (二)、SiO2结构 (三)、VA、VIA族亚金属结构§6 聚合物晶态结构(一)、晶胞结构 (二)、晶态结构模型 (三)、聚合物结晶形态§7 非晶态结构第三章晶体缺陷(12学时)实际晶体常存在各种偏离理想结构的区域晶体缺陷。
根据晶体缺陷分布的几何特征可分为点缺陷、线缺陷和面缺陷三类。
第5章材料的形变和再结晶
提纲
5.1 弹性和粘弹性
5.2 晶体的塑性变形(重点)
5.3 回复和再结晶(重点)
5.4 高聚物的塑性变形
学习要求
掌握材料的变形机制及特征,以及变形对材料组织结构、性能的影响;冷、热加工变形材料的回复和结晶过程。
1.材料的弹性变形本质、弹性的不完整性及黏弹性;
2.单晶体塑性变形方式、特点及机制(滑移、孪生、扭折)
3.多晶体、合金塑性变形的特点及其影响因素
4.塑性变形对材料组织与性能的影响;
5.材料塑性变形的回复、再结晶和晶粒长大过程;
6.影响回复、再结晶和晶粒长大的诸多因素(包括变形程度、第二相粒子、工艺参数等)
7、结晶动力学的形式理论(J-M-A方程)
8、热加工变形下动态回复、再结晶的微观组织特点、对性能影响。
9、陶瓷、高聚物材料的变形特点
重点内容
1. 弹性变形的特征,虎克定律(公式),弹性模量和切变弹性模量;
材料在外力作用下发生变形。
当外力较小时,产生弹性变形。
弹性变形是可逆变形,卸载时,变形消失并恢复原状。
在弹性变形范围内,其应力与应变之间保持线性函数关系,即服从虎克(Hooke)定律:
式中E为正弹性模量,G为切变模量。
它们之间存在如下关系:
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结
构不敏感参数。
在工程上,弹性模量则是材料刚度的度量。
2. 弹性的不完整性和粘弹性;
理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等。
3. 滑移系,施密特法则(公式),滑移的临界分切应力;
晶体中一个滑移面和该面上一个滑移方向组成。
fcc和bcc,bcc的滑移系?滑移系多少与塑性之间的关系。
滑移的临界分切应力:
如何判断晶体中各个滑移系能不能开动?
解释几何软化和几何硬化?为何多晶体塑性变形时要求至少有5个独立的滑移系进行滑移?
4. 滑移的位错机制,派-纳力(公式);
为什么晶体中滑移系为原子密度最大的面和方向?
5. 比较塑性变形两种基本形式:滑移与孪生的异同特点;
6. 多晶体塑性变形的特点:晶粒取向的影响,晶界的影响;
会判断多个晶体中哪些晶体会优先发生塑性变形?
7. 细晶强化与Hall-Petch 公式, 高温晶界弱化的原因;
晶粒细化为何能同时提高材料的强韧性?
位错塞积群效应(应力集中区的应力数值等于外加切应力n 倍)
可启动临近晶粒滑移,故
高温合金为何要采用定向凝固技术获得单晶?
晶界滑动机制和扩散性蠕变
8. 固溶强化,屈服现象(吕德斯带),上下屈服点的柯垂耳理论和一般位错增殖理论,应变时效;
d c dc
ττ= 金属有四大著名的强化机制,请给出这几种机制的名称,物理实质,定量描述其强化效果的数学公式。
请简洁回答要点。
9. 弥散强化,不可变形粒子的绕过机制(公式),可变形粒子的强化机理;
2Gb Gb R τλ
== 10. 冷变形后的显微组织和亚结构, 加工硬化概念(公式);
11. 单晶体与多晶体力学性能(应力应变曲线)比较
12. 形变织构与残余应力;
常见丝织构和板织构,残余应力分类
13. 回复动力学,激活能求法(公式)与回复机制(低温,中温,高温);
14. 再结晶形核机制(弓出机制公式),再结晶动力学,J-M方程和
Avrami方程(公式);
15. 再结晶激活能(公式),求不同温度下再结晶相同分数的时间(公
式);
16. 再结晶温度及其影响因素,影响再结晶晶粒大小的因素;
变形程度
原始晶粒尺寸
第二相的影响
再结晶退火工艺参数(加热温度
、温升快慢、保温时间等)
控制晶粒大小?
17. 晶粒长大动力学(公式),晶界移动速率(公式)和晶界迁移激
活能求法(公式);
驱动力:
18. 晶粒的正常长大及其影响因素;尤其是分散相粒子作用(公式)
始晶粒大小
温度
可溶解的杂质或合金元素
不溶解的第二相
晶粒间的位向差
热蚀沟
19. 二次再结晶,再结晶后的组织(晶粒大小,织构,孪晶);
20. 一次与二次再结晶以及静态再结晶的区别;
21. 冷、热加工的区别,回复再结晶分类;
22. 动态回复,动态再结晶;
23. 热加工后的性能和组织;
24. 蠕变的概念,典型曲线以及机制;
25. 超塑性概念,本质;
26. 陶瓷材料的变形特点;
陶瓷晶体,由于其结合键(离子键、共价键)的本性,再加上陶瓷晶体中的滑移系少,位错的b大,故其塑性变形相对金属材料要困难得多,只有以离子键为主的单晶陶瓷才能进行较大的塑性变形。
27. 高聚物变形的特点。
对于高分子材料,其塑性变形是靠粘性流动而不是靠滑移产生的,故与材料粘度密切相关,而且受温度影响很大。
重要概念和公式(这里不是最全面)
弹性变形,弹性模量,包申格效应,弹性后效,弹性滞后,粘弹性;塑性变形,滑移,滑移系,滑移带,滑移线,交滑移,双交滑移;
临界分切应力,施密特因子,软取向,硬取向,派-纳力;
孪生,孪晶面,孪生方向,孪晶,扭折;
固溶强化,屈服现象,应变时效,加工硬化,弥散强化;
形变织构,丝织构,板织构,残余应力,点阵畸变,带状组织,流线;回复,再结晶,晶粒长大,二次再结晶,冷加工,热加工,动态再结晶;
储存能,多边化,回复激活能,再结晶激活能,再结晶温度;
弓出形核,临界变形量,再结晶织构,退火孪晶;
虎克定律:
,
滑移的临界分切应力:
Peierls-Nabarro力:
Hall-Petch公式:
弥散强化关系式:
聚合型合金强化关系式:
加工硬化关系式:
回复动力学:
再结晶动力学:
再结晶的极限平均晶粒直径:
再结晶晶粒大小与温度之间的关系:
材料在外力作用下发生变形。
当外力较小时,产生弹性变形。
弹性变形是可逆变形,卸载时,变形消失并恢复原状。
在弹性变形范围内,其应力与应变之间保持线性函数关系,即服从虎克(Hooke)定律:
式中E为正弹性模量,G为切变模量。
它们之间存在如下关系:
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量。
实际上,理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等。
对非晶体,甚至对某些多晶体,在较小的应力时,可能会出现粘弹性现象。
粘弹性变形是既与时间有关,又具有可恢复的弹性变形,即具有弹性和粘性变形量方面特征。
粘弹性变形是高分子材料的重要力学特性之一。
当施加的应力超过弹性极限时,材料发生塑性变形,即产生不可逆的永久变形。
通过塑性变形,不但可使材料获得预期的外形尺寸,而且可使材料内部组织和性能产生变化。
单晶体塑性变形的两个基本方式为滑移和孪生。
滑移和孪生都是
切应变,而且只有当外加切应力分量大于晶体的临界分切应力 C时才能开始。
然而,滑移是不均匀切变,孪生为均匀切变。
对于多晶体而言,要求每个晶粒至少具备由5个独立的滑移系才能满足各晶粒在变形过程中相互制约和协调。
多晶体中,在室温下晶界的存在对滑移起阻碍作用,而且实践证明,多晶体的强度随其晶粒细化而提高,可用著名的Hall-Petch公式来加以描述:
至于合金为单相固溶体时,由于溶质原子存在会呈现固溶强化效果,对某些材料还会出现屈服和应变时效现象;当合金为多相组织结构时,其变形还会受到第二相的影响,呈现弥散强化效果。
而陶瓷晶体,由于其结合键(离子键、共价键)的本性,再加上陶瓷晶体中的滑移系少,位错的b大,故其塑性变形相对金属材料要困难得多,只有以离子键为主的单晶陶瓷才能进行较大的塑性变形。
对于高分子材料,其塑性变形是靠粘性流动而不是靠滑移产生的,故与材料粘度密切相关,而且受温度影响很大。
材料经塑性变形后,外力所做的功部分以储存能形式存在于材料内部,从而使系统的自由能升高,处于不稳定状态。
故此,回复再结晶是材料经过冷变形后的自发趋势,加热则加快这一过程的发生。
当加热温度较低,时间较短时,发生回复。
此时,主要表现为亚结构的变化和多边化过程,第一类内应力大部消除,电阻率有所下降,而对组织形态和力学性能影响不大。
当加热温度较高,时间较长时就发生再结晶现象。
再结晶时,新的无畸变等轴晶将取代冷变形组织,其性能基本上回复到冷变形前的
状态。
再结晶完成后继续加热时,晶粒将发生长大现象。