第9讲 矩形单元和6节点三角形单元
- 格式:ppt
- 大小:1000.00 KB
- 文档页数:19





有限元分析及应用大作业课程名称: 有限元分析及应用班级:姓名:试题2:图示薄板左边固定,右边受均布压力P=100Kn/m作用,板厚度为0.3cm;试采用如下方案,对其进行有限元分析,并对结果进行比较。
1)三节点常应变单元;(2个和200个单元)2)四节点矩形单元;(1个和50个单元)3)八节点等参单元。
(1个和20个单元)图2-1 薄板结构及受力图一、建模由图2-1可知,此薄板长和宽分别为2m和1.5m,厚度仅为0.3cm,本题所研究问题为平面应力问题。
经计算,平板右边受均匀载荷P=33.33MPa,而左边被固定,所以要完全约束个方向的自由度,如图2-2所示。
取弹性模量E=2.1×11Pa,泊松比μ=0.3。
P=33.33MPa图2-2 数学模型二、第一问三节点常应变单元(2个和200个单元)三节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用2个单元的网格划分后的结果如图2-3,200个单元的网格划分图如图2-6所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-4、7所示,应力云图如图2-5、8所示。
图2-3 2个三角形单元的网格划分图图2-4 2个三角形单元的位移云图图2-5 2个三角形单元的应力云图图2-7 200个三角形单元的位移云图三、第二问四节点矩形单元的计算四节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用1个单元的网格划分后的结果如图2-9,50个单元的网格划分图如图2-12所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-10、11所示,应力云图如图2-13、14所示。
图2-9 1个四边形单元的网格划分图图2-11 1个四边形单元的应力云图图2-12 50个四边形单元的网格划分图图2-13 50个四边形单元的位移云图图2-14 50个四边形单元的应力云图四、第三问八节点等参单元的计算四节点单元类型为PLANE82,设置好单元类型后,实常数设置板厚为0.3M。


第六单元(组合图形)教学计划【单元教学内容】图形的面积【单元教材分析】学生在以前的学习中已经掌握了长方形、正方形、平行四边形、三角形、梯形的面积计算方法。
在此基础上学习组合图形,一方面可以巩固已学的基本图形,另一方面则能将所学的知识进行综合,提高学生的综合能力。
为体现这一思想,本单元安排了两个情境活动:在“组合图形面积”中,重点探索计算组合图形面积的方法;在“探索活动”中,主要学习不规则图形面积的估计与计算。
在现实生活中,学生将接触到大量的不规则图形的面积问题,原来这些内容都不安排在教材中,而根据《标准》的要求,让学生掌握估计、计算不规则图形的面积,是培养学生空间观念的一个方面,同时也是提高学生解决实际问题能力的一个方面。
为此,教材专门安排了估计、计算不规则图形的面积。
通过这些内容,让学生掌握解答组合图形面积的基本能力。
【教学目标】1、在探索活动中,归纳组合图形面积的计算方法。
2、能正确计算组合图形的面积,并能解决相应的实际问题。
3、能估计不规则图形的面积大小,并能用不同方法计算面积。
【重点难点】正确计算不规则图形的面积【教具学具】直尺、三角板、方格纸、小黑板。
【单元课时安排】共12课时第1课时(总第82课时)【教学内容】组合图形的面积【教学目标】1、在自主探索的活动中,理解计算组合图形面积的多种方法。
2、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
3、能运用所学的知识,解决生活中组合图形的实际问题。
【重点难点】1、理解计算组合图形面积的多种方法。
2、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
【教学准备】课件及一些基本图形学具(长方形、正方形、三角形、平行四边形、梯形) ,发给学生每人一张的课上所用的主题图形。
【教学过程】第2课时(总第83课时)【教学内容】组合图形的面积练习课【教学目标】1、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
2、能运用所学的知识,解决生活中组合图形的实际问题。


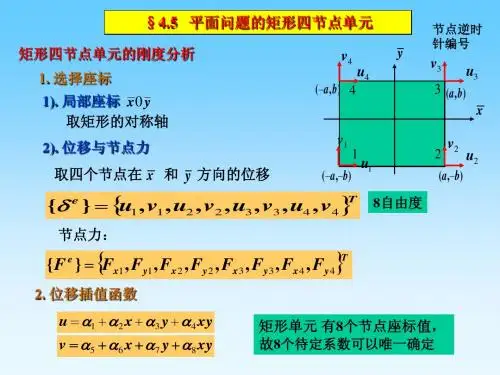
§2.9平面问题单元划分有限元法在平面问题进行分析时,才采用三角形单元和四边形单元、或者矩形单元,三角形单元的优点是简单且对结构的不规则边界逼近好,而矩形单元却更能反映实际弹性体内部的应力应变变化。
这两点我们会逐渐向大家说明。
所以一般说来,有限元分析,单元划分的密度和单元种类选取,对计算结果起重要作用。
一般单元划分越密集,结果越精确。
单元多也导致求解的线性方程组阶数增高,要求计算机的内存也更大,计算的时间也越长,分析的效率就越低。
解决这一矛盾的方法就是在应力集中区域单元划分密集一些,应力变化梯度小的位置,划稀疏些,这样就能兼顾精度与效率的关系。
一般的原则是:1)根据结构的受力和支承特点,按对称和反对称的性质,简化分析模型,以减少计算分析的规模。
2)合理布局单元的密集程度,以使计算结果精度高而计算量小。
3)在同一单元内,单元的特性数据和材质数据应保持一致。
4)集中载荷的作用点和载荷密度突变处应有节点。
5)在欲知道应力状态、内力情况和位移值的位置应有节点。
6)单元的选取欲分析的目标密切相关。
模型的单元划分好后,把所有的单元和节点按一定的规律和顺序进行编号,选择适当的坐标系(直角、柱面和球面),以方便确定各节点的坐标值。
§2.10 节点位移、节点力和节点载荷弹性体在承受外力作用后,其内力的传递实际是通过单元之间的边界来实现的。
但我们把结构离散化后,如果单元划分得足够小时,可以看成为其内力的传递通过单元与单元之间的节点进行传递。
对于平面问题而言,每个节点都有位移和力两个未知量,这两个量又都是x、y的函数,注意平面问题的节点是不能传递力矩的,为什么?一,节点位移对三节点三角形单元而言,因有三个节点,每个节点的位移都有x ,y 两个分量,所以一共有6个自由度。
单元节点位移向量可表示为:{}[]Tm m j j i ie v u v u v u =δ二,节点力所谓节点力,就是单元对节点或节点对单元作用的力,它是弹性体内部的作用力,也就是我们常说的内力。