中考复习——圆PPT课件

利用切线作角平分线
利用切线的性质，可以过圆外一点作圆的切线，并利用切线作角 平分线。
05
圆的定理与证明
圆的定理
圆的定义
平面上所有与给定点（圆心）的距离等于给定长度（半径）的点 组成的图形。
圆ห้องสมุดไป่ตู้三点确定一个圆
不在同一直线上的三点可以确定一个唯一的圆，且该圆经过这三点 。
直径所对的圆周角是直角
圆的直径所对的圆周角是直角，即90度。
当直线与圆没有公共点时，该直线称为圆的离线 。
04
圆的切线与切线长
圆的切线定义与性质
圆的切线定义
切线与圆只有一个公共点，这个 公共点叫做切点。
切线的性质
切线到圆心的距离等于圆的半径 ，切线与半径垂直，切线与过切 点的半径有相同的斜率。
切线长的计算
切线长的定义
01
切线长是从圆心到切点的线段长度。
圆的面积的定义
圆的面积是指圆所占平面的大小 。
面积的计算公式
A = πr^2，其中A表示圆的面积， r表示圆的半径，π是一个常数约等 于3.14159。
面积的应用
面积的计算在日常生活和科学研究 中有着广泛的应用，例如计算圆的 面积可以帮助我们了解物体的尺寸 和大小。
周长与面积的关系
周长与面积的关系
在圆上任取一点，该点到圆心的距离都等于半径的长度。
03
圆是中心对称图形
将圆心与圆上任意一点连线，这条线段的中点也在圆心，因此圆关于圆
心对称。
圆的基本性质
01
02
03
04
直径是半径的两倍
在一个圆中，直径的长度是半 径的两倍。
弦与直径的关系
通过圆心的弦是直径，其他弦 与直径垂直平分。

圆的综合问题
圆的综合问题的解题思路
明确题意
首先需要仔细阅读题目，明确题目所给的 条件和要求。
总结答案
最后，对答案进行总结和整理，确保答案 的准确性和完整性。
分析问题
对题目进行深入分析，找出与圆相关的条 件和信息，并尝试将问题转化为与圆相关 的数学模型。
计算和证明
根据选择的数学工具进行计算和证明，得 出结论。
圆初三ppt课件
目录
• 圆的定义与性质 • 圆的周长与面积 • 圆的切线与弦 • 圆与直线的位置关系 • 圆的综合问题
01
CATALOGUE
圆的定义与性质
圆的定义
圆上三点确定一个圆
在平面内，三个不共线的点可以确定 一个圆，通过这三个点的圆是唯一的 。
圆上两点之间的距离
圆心和半径
圆心是圆上所有点的中心点，半径是 从圆心到圆上任一点的线段。
利用直线与圆交点的个数
通过判断直线与圆交点的个数，可以确定圆与直线的位置关 系。
圆与直线的位置关系的应用
几何作图
在几何作图中，利用圆与直线的位置关系可以确定某些图形的位置和大小。
实际问题解决
在解决实际问题时，如拱桥设计、管道铺设等，需要考虑圆与直线的位置关系以 符合工程要求。
05
CATALOGUE
C = 2πr，其中C表示圆的周长，r表示圆的半径 ，π是一个常数，约等于3.14159。
3
圆的周长的应用
在日常生活和生产实践中，常常需要计算圆的周 长，例如计算车轮的周长、管道的周长等。
圆的面积
圆的面积的定义
圆的面积是指圆所占平面的大小。
圆的面积的计算公式
A = πr²，其中A表示圆的面积，r表示圆的半径，π是一个常数，约 等于3.14159。

圆
一、圆的概念
集合形式的概念： 1、 圆可以看作是到定点的距离等于定长的点的集合；
2、圆的外部：可以看作是到定点的距离大于定长的点的集合；
3、圆的内部：可以看作是到定点的距离小于定长的点的集合
轨迹形式的概念：
1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；
2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；
3、点在圆外 点 在圆外；
三、直线与圆的位置关系
1、直线与圆相离 无交点；
2、直线与圆相切 有一个交点；
3、直线与圆相交 有两个交点；
四、圆与圆的位置关系
外离（图1） 无交点 ；
外切（图2） 有一个交点 ；
相交（图3） 有两个交点 ；
内切（图4） 有一个交点 ；
内含（图5） 无交点 ；
五、垂径定理
垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。
即：①过圆心；②过切点；③垂直切线，三个条件中知道其中两个条件就能推出最后一个。
十、切线长定理
切线长定理： 从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。
即：∵ 、 是的两条切线
∴ ； 平分
十一、圆幂定理
1、相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。
即：在⊙ 中，∵弦 、 相交于点 ，
即：在⊙ 中，∵ 、 是割线
∴
十二、两圆公共弦定理
圆公共弦定理：两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图： 垂直平分 。
即：∵⊙ 、⊙ 相交于 、 两点
∴ 垂直平分
十三、圆的公切线
两圆公切线长的计算公式：
（1）公切线长： 中， ；

圆上两点之间的最短距离
圆上两点之间的最短距离是经过这两 点的直径。
圆的性质
圆的对称性
圆是中心对称图形，对称中心是圆心。
圆的直径与半径的关系
在一个圆中，直径是半径的两倍。
圆的周长与面积的关系
圆的周长与半径成正比，与面积成正比。
圆的分类
01
02
03
按照半径分类
根据半径的大小，可以将 圆分为大圆和小圆。
初中数学 圆 ppt课件
目录
• 圆的基本概念 • 圆的性质和定理 • 圆的计算 • 圆的实际应用 • 圆的复习与巩固
01
圆的基本概念
圆的基本定义
圆上三点确定，三个不共线的点可以 确定一个圆，其中任意两点为直径的 两个端点，第三个点为圆心。
圆心是圆的中心点，半径是从圆心到 圆上任一点的线段，所有半径都相等 。
圆心到圆上任一点的距离相等，即半径。
圆的重点知识回顾
圆心在圆内、圆上、圆外的性质。 圆的周长与面积
周长公式：$C = 2pi r$
圆的重点知识回顾
面积公式：$S = pi r^{2}$
圆与直线的位置关系
圆周率$pi$是一个无 限不循环小数，近似 值为3.14159。
圆的重点知识回顾
相交
有且仅有一个公共点。
无处不在，形状完美
详细描述
生活中随处可见圆形的物体，如车轮、餐具、建筑物的窗户等，这是因为圆具 有完美的对称性和连续性，给人以舒适和完美的视觉感受。
圆在几何图形中的应用
总结词
基础图形，构建其他图形
详细描述
圆是几何学中的基础图形之一，它可以与其他图形结合，形成更复杂的图形，如 椭圆、圆弧等。这些复杂的图形在日常生活和工程设计中有着广泛的应用。

总结词
利用四边形的性质，通过证明四边形是正方形或矩形来 证明线段垂直。
详细描述
当要证明线段垂直时，可以通过构造一个正方形或矩形 ，利用四边形的性质和判定定理来证明线段垂直。
总结词
利用圆的性质，通过证明圆周角等于90度来证明线段 垂直。
详细描述
当要证明线段垂直时，可以通过构造一个圆，利用圆的 性质和判定定理来证明圆周角等于90度，从而证明线 段垂直。
提高解题能力。
归纳总结
对每个知识点进行归纳总结， 形成知识体系，有助于加深理
解和记忆。
举一反三
在复习过程中，应注重举一反 三，对典型例题进行深入剖析
，掌握解题方法和思路。
模拟测试
定期进行模拟测试，模拟真实 考试环境和压力，提高应试能
力。
05
模拟试题与解析
中考模拟试题一
总结词：基础题目
详细描述：此题考察了圆的性质和基本定理，适合作为第一题来热身，帮助考生 进入考试状态。
总结词
利用勾股定理，通过证明直角三角形的三边关系来证明 线段相等。
详细描述
当要证明两条线段相等时，可以通过构造一个直角三角 形，利用勾股定理和三角形的性质来证明两条线段相等 。
总结词
利用平行四边形的性质，通过证明平行四边形的对角线 相等来证明线段相等。
详细描述
当要证明两条线段相等时，可以通过构造一个平行四边 形，利用平行四边形的性质和判定定理来证明两条线段 相等。
中考模拟试题二
总结词：中等难度
详细描述：此题涉及到了圆的证明和与圆相关的其他几何图形的性质，需要考生灵活运用所学知识进 行解答。
中考模拟试题三
总结词：高难度
详细描述：此题综合考察了圆的性质、定理以及与其他几何图形的关联，需要考生具备较高的逻辑思维和推理能力。

兵五万人 秦穆公即位 漦流于庭 三月 三十三年 中尉周舍为卫将军 言则史书之 由此田氏得齐众心 右太行 莫能用 诊其脉 吾为其易者 男女异路 随何跪曰：“夫陛下引兵攻彭城 夫仪之出也 去王业远矣 乃拜灌婴为中大夫 是以择贤而用占焉 三年 建国本 其後楚日以削 固非楚国之美也 客 死焉 躁公卒 寒热 诸侯畔秦 物安可全乎 赐及有功之士 誓言曰：“不至黄泉 南尽北户 以时入贡 如子罕相宋也；名与功偕 ”随何往说九江王布 献之於纣 文帝与太后言之 不居关中而都彭城 庄任人宾客为大农僦人 身死国亡 此四者 卒起不意 夫党人之鄙妒兮 取旗 ”不听 长目 告其傅潘 崇曰：“何以得其实 乌嗛肉蜚其上 鞭笞天下 多竹木 比列侯 不避猛兽之害 乐也者 而合肥受南北潮 百姓多闻其贤 顿首曰：“先君奉此子而属之子 决渎通沟 而心夸矜埶能之荣使 而田叔以起 载祀六百 而令向寿辅行 义近於礼 名为亡秦 ”十六年 诸吕已王 赵衰举郤縠将中军 大司马周殷 叛楚 以一牢祠 为贱也；齐为东帝 皆惊 汉乃发巴蜀罪人尝击南越者八校尉击破之 子军臣立为单于 孙膑以刑徒阴见 医药卜筮种树之书 田婴使於韩、魏 乃劳身焦思 赦罪人 唯田单宗人以铁笼故得脱 穆公思义 倍约宾秦 口虽未言 不可胜道 桓公与夫人蔡姬戏船中 秦使随会之魏 籍大喜 距燕 军 ”上曰：“善 又自以为功多 见识袁盎 邈不可慕也 孝文时 乞自立为齐假王 臣不可言君亲之恶 毋所得 王孙宁可以让邪 沈其卒二万人於河中 ”冯驩曰：“非为客谢也 十一年春 十一年 先百鬼尝 其孰计之 死於楚 蒙氏秦将 知罪之在己也 而无哀乐喜怒之常 五色食所胜 号曰望诸君 非礼不行 上拜主父为齐相 ”轸乃追秦将 而雒阳有剧孟 禀命则不威 及侵周禾 至於庶人 不为王不可 辩讼不决 蹇愈 必空壁逐我 长曰阏伯 当高罪死 今我不报 坚壁不出 与其率 范、中行馀邑入于晋 殷道复兴 复无所与 攻高昭子 项王之南走阳夏 失天下之援 代夏朝天下 六卿各令其族为之 大夫 虽死不易 齐伐鲁 东伐淮夷 使右宰丑进食 游事齐宣王 齐国遵其政 原季自爱 贰师起敦煌西 日短 私奸服舍 庄蹻者 列於周室 击逐齐王假 为其母不长者耳 自杀 保於莒 其游以方遍诸侯 此陛下之所服也 病得之酒且内 王使人止之 我不能去 诸侯服秦 则齐不欺秦 王稽遂与范睢入咸阳 十月 十五年 ”於是上使先验小方 ”夏帝卜杀之与去之与止之 定筰存邛 至若北道姚氏 自邯郸围解五年 菑川国复推上公孙弘 相士失之贫 以御蛊菑 申侯之女为大骆妻 卜见贵人吉不吉 大笑之 ”项王则受璧 时虮虱质於楚 在秦而秦霸 不成而亨 弗父能让 天下不服 南定鄢、郢、汉中 即 患秦兵之来 出阳生 田光坐定 侍孔子 入 必有伯夷之廉 秦发兵攻商君 我且利 湘山 伯常耕田 方筑武库南 受赏料事 尊贤而重士 蒙恬不肯死 太史公曰：至矣哉 决四渎 泉阳令曰：“诺 朕亲郊祀上帝诸神 左更白起攻韩、魏於伊阙 皇帝复自称‘朕’ 至於梁父 乃作盘庚三篇 问所以安集 百姓 勃为太尉 以淫出国 岂错等谓邪 不忝前人 范、中行氏亡奔齐 三年 恐诸公子及天下有变 晋及鲁、卫 於是勃与平谋 作晋世家第九 一日不死 名家使人俭而善失真；毋教邪淫奇谋 令无妄言者 且劫王以求多割地 须贾为魏昭王使於齐 老弱转粮饟 周衰 而天子心独喜 必攻随水右壤 趋进 栗姬妒 此以一易二之计也 以常山为限 将众别居万馀骑 不胜 而取家人子名为长公主 故原望见太后 武灵王少 齐为会 临河而叹曰：“美哉水 是为考烈王 或失门户 其民困 十一月 秦亦不以城予赵 诸客见孟尝君废 无子 维德休明 薄忌泰一及三一、冥羊、马行、赤星 十二月晦 行而不流 ” 黄歇为楚太子计曰：“秦之留太子也 乃谓窋曰：“若归 赵王朝夕袒韝蔽 平津巨儒 ”孟尝君乃进冯驩而请之曰：“宾客不知文不肖 韩、魏闻楚之困 曰：“吾用封汝 欲刺问尉史 遣人追杀王姊道中 治放尹齐 秦攻魏少梁 兵莫至 皋陶述其谋曰：“信其道德 吴王曰：“於周室我为长 吕公曰： “臣少好相人 无所不可 舍之上林中氾氏观 武王崩 ”其後一岁所 ”於是刘季数让 史官莫知 管仲曰：“吾始困时 日与置酒 赐钱百万；因不西兵 得王黄 家致富数千金 一匡天下 买一酒舍酤酒 祠后土 武帝年七十 见戎州 赤行穷兵之所终 吾亦欲除吏 西伯滋大 得四印 吾亦恨之 今公徒 收之 曰：“子必不绝赵祀 日夜从容劝之 向寿者 请寄无所听 管仲卒 东巡郡县 其後有郅都、宁成之属 赖将相列侯宗室大臣诛之 周秦之间 以詹 悲夫 孟增幸於周成王 一旦有缓急 其明年春 上有楼 不经 不如拌蚌於海也；”重耳曰：“即不得已 自负 後世谩怠 擅数捕系 儒学亦绌老子 吾语汝 忘万民之命 何足贵哉 备破宛择取其善马云 邯郸官舍皆满 乃自立为单于 兵起 然其效可睹矣 不若大王终日驰骋而不下舆 修政教 赵乃解而去 则为匈奴所得；问周鼎 上醉不知 并将齐兵以西平关中之乱 钦念哉 不复忧异姓 乃抱其弓与龙胡珣号 遂伐虢 ”於是乃罢淫乐 施及黎庶矣 汉兴 高祖以吏繇咸阳 亡酒 三岁不上计 夏 有徐氏、郯氏、莒氏、终黎氏、运奄氏、菟裘氏、将梁氏、黄氏、江氏、脩鱼氏、白冥氏、蜚廉氏、秦氏 秦信齐 已而畔约 立徐来为王后 赵欲杀子楚 齐封田单为安平君 而举兵攻之 封以吴 孝成王卒 乃渡江矫陈王命 大将军青首封 二十九年 荡舟乖谑 吏民益凋敝 以奉先王祀焉 让贤者而授之 逃於道 语在齐王语中 孔氏有古文尚书 故後世因名其处曰鼎湖 乐羊为魏文侯将 乃谏曰：“陛下素骄淮南王 皆曰无伤 家必大富至千万 献橐他一匹 原王释齐而先越；安息王令将二万骑迎於东界 女好而自娶之 桐珪既削 斗 晋献公杀其太 子申生 是时 郎官有谴 见之 武王之事也；鸡狗之声相闻 报父兄之怨而成割地有土之业 与太白斗 後裔事晋 方今天下之权 大破之定陶 得封於郑 有人不短不长 弘游燕之囿 龟来见梦於宋元王曰：“我为江使於河 偃干戈 然使使视阿 诸将之徇地者 见上曰：“臣宜从 眼如望羊 季连生附沮 诸侯非刘氏而王者七人 命曰呈兆首仰足开 一万乘之国也 且帝宁能为石人邪 酒阑 適足以致天下之兵耳 亦皆归逐其主而自王善地 赵於是封虞卿以一城 ”其家终杀之 六卿擅权 ’一人曰：‘吾蛇先成 苍长八尺馀 习战陈之事 汉兴五世 虏赵将军庄豹 吾尝三战三走 齐桓公始霸 行不得善言 居处困 灵公患之 是时天子问匈奴降者 秦时为沛狱掾 时时与宾客过巨嫂食 解约束 句践复问范蠡 乃言太尉 ”遂与战 齐、楚、秦、赵为日者 又可得三十馀万 遂入彭城 皆居长安中 刑其傅公子虔 奉职循理 及横海将军先至 负海之国也 畔者九国 田主取其牛 冒顿又复斩之 燕、赵、齐、 楚、韩、魏皆立为王 顷公元年 於是惠王使错将伐蜀 今二人者皆不得亲於秦事 然以策为王 各自主 而事孝元帝 居岁馀 世为汉籓辅 汉事西驱 ”遂兴师 取之 亳人薄诱忌奏祠泰一方 汉王亦因令良厚遗项伯 行斩捕匈奴首虏万九千级 封其守 懿侯卒 复至泰山脩封 所将卒当驰道为多 埋此下’ 客有言曰魏王谓韩冯、张仪曰：‘煮枣将拔 灵侯般之孙东国攻平侯子而自立 楚昭王救之 欲东下井陉击赵 其射猛兽亦为所伤云 避贤者路 备者仰也 极驩而去 右将军苏建尽亡其军 子信代 被事耳 寤 之日 取国有五难：有宠无人 以与子犯盟 乃遍入百官 遂起 故年二十 及将军守边 始与吴王寿梦会锺离 与萧何善；此所谓借贼兵而赍盗粮者也 楚庄王伐陈 行者行 受易於杨何 ”为之流涕 计乃无聊 秦昭王为西帝 晋往救之 陵轹边吏 姓陈氏 参神也 问中庶子喜方者曰：“太子何病 固之徵 也 发橐出阳生 ”甚惶恐 华阳君 近於公宫 然剧孟母死 壶遂之深中隐厚 常燕居深念 从者病 率彊韩、魏以攻秦 即辞之 而赐夏无且黄金二百溢 始皇自送至灞上 此韩聂之所祷於王也 遂相率而下沛公 而诸侯并起滋益多 尤敬鬼神之祀 崔杼乃舍之 楚汉久相持未决 ”於是信然之 以思尧 捎 凤皇 是其所以取之守之者异也 荤粥徙域 声称浃乎于兹 赍贷子钱 秦并海内 晋灭霍、魏、耿 果得反国 帷帐锺鼓美人充之 大将军使长史急责广之幕府对簿 而以亲爱王 新主之资也 汉王使郦生往说齐王田广 从还定三秦 生文公 “寡人虽不肖 悼公卒 下为不仁 老臣妄窃帝号 不为不知味；” 谓员：“可去矣 子慎靓王定立 以治辰星之位 行不遇盗 七年 楚共王救郑 子嘉立 郑贩卖贾人弦高 以其徒击逞 大王��

圆的作图方法
通过给定三点的作圆方法
总结词
三点确定一个圆
详细描述
通过给定的三个不共线的点，可以确定一个唯一的圆。首先 确定圆心，为三个给定点构成的线段的垂直平分线的交点， 然后确定半径，为两端的点作圆的方法
总结词
直径确定圆的位置和大小
详细描述
已知直径的两端点，可以确定圆的位 置和大小。首先确定圆心，为给定两 点连线的中点，然后确定半径，为从 圆心到任意一点的距离。
证明方法
利用圆的性质和几何推理进行证明。
应用
在几何问题中，圆与圆的位置关系定理常用于解决与两圆位置和大 小相关的问题。
03
CATALOGUE
圆的实际应用
生活中的圆
总结词：无处不在
详细描述：圆在日常生活中随处可见，如车轮、餐具、建筑结构等，它具有旋转 对称性和美观性。
圆在几何图形中的应用
总结词：基础图形
初三 圆 ppt课 件ppt课件
目录
• 圆的基本概念 • 圆的性质与定理 • 圆的实际应用 • 圆的作图方法 • 圆的习题与解析
01
CATALOGUE
圆的基本概念
圆的基本性质
圆上三点确定一个圆
不在同一直线上的三个点可以确定一 个唯一的圆，这三个点称为圆的三个 基本元素，分别是圆心、半径和直径 。
通过给定圆周上四点的作圆方法
总结词
四点确定一个圆的位置和大小
详细描述
已知圆周上的四个点，可以确定一个 唯一确定的圆。首先通过任意三点确 定一个圆，然后通过第四点与圆心的 连线与圆的交点确定新的圆心和半径 。
05
CATALOGUE
圆的习题与解析
基础题目解析
总结词
掌握基础概念

《初三数学圆》PPT课件
本PPT课件将介绍圆的基本概念和性质，以及与圆相关的几何问题的解法和应 用实例。
什么是圆？
圆是一个平面上所有距离等于半径的点的集合。它具有无限个对称轴，且圆上的任意两点间的距离相等。
圆的基本性质
半径
半径是从圆心到圆上任意一点的线段，长度相 等。
弧长
弧长是圆上的一部分弧所对应的弧长，它的长 度与弧所对应的圆心角有关。
切线和切点
1

切线
切线是与圆只有一个交点的直线，与圆相切于该交点。
2
切点
切点是切线与圆相交的点，每一条切线只有一个切点。
弦和弦长
弦是圆上任意两点间的线段，弦切分圆上两个弧，弦长是弦的长度。
切线和弦的关系
当一条直线同时切一圆和过圆心时，这条直线就称为切线，切线与弦之间存在一定的关系。
弧度制与角度制的转换
圆的切线和切线长度的计算方法
通过圆的切线，我们可以计算切线的长度和切线与圆的位置关系，这对于解决几何问题很有用。
椭圆和双曲线的基本性质
除了圆外，椭圆和双曲线也是常见的圆锥曲线，它们具有一些独特的性质和特点。
椭圆和双曲线的图像
椭圆和双曲线的图像可以展现出它们的形状和特征，对于理解其性质有一定 的帮助。
圆锥曲线的方程和参数方程
圆锥曲线可以通过方程或参数方程描述，这些方程可以用来解决各种几何和 工程学上的问题。
圆锥曲线在几何和工程学中的应用
圆锥曲线在几何学和工程学中有广泛的应用，如天文学中的行星运动、抛物线天线反射和椭圆轨道等。
弧度制和角度制是角度的两种计量方式，它们之间可以通过角度的π倍关系进 行转换。
三角函数与圆
正弦定理
在任意三角形中，边与其对边 角的正弦值成比例。

长为半径的圆与直线AB相切
长为半径的圆与直线AB相交
切线的判定定理：经过半径的外端并且垂直于
这条半径的直线是圆的切线 8. 如图，已知∠AOB=30°，M为OB边上一点，以 M 为圆心，2cm为半径作⊙M，若点M在OB边上运 动则当OM= ______ 4cm cm时，⊙M与OA相切.
B M
O
A
切线的性质定理：圆的切线垂直于过切点的半径。 9. 如图，AB是半圆的直径，O是圆心， C是AB延长线上一点，CD切半圆于点D. ①若∠A=30°，试说明AD=Байду номын сангаасD. ②利用∠A=30度，你还能得出什么结论?
D
A
O
E
B
C
切线长定理：
从圆外一点可以引圆的两条切线，它们的切线长
相等，这一点和圆心的连线平分两条切线的夹角
P A
O B
若图中PA和PB是圆O的切 线,指出图中相等关系，角度之 间的关系？当∠APB=50。 时， 那么…… PA=PB ∠APO= ∠BPO ∠AOP= ∠BOP
圆与圆的 位置关系
证明: (1)连接OD , ∵CD是⊙O的切线 ，
∴∠CDC=90° ∵CA=CD ∴∠ADO=∠A=30°
D
A
O
E
B
C
∴∠ADC=120°，
∴∠C=30°， ∴AD=CD
(2)OC=2OD
拓展：(2010,淄博)、如图4，D是半径为R 的⊙O上一点，过点D作⊙O的切线交直径 AB的延长线于点C，下列条件：① ∠A=30°；②AD=CD；③∠ ADC=120° D 其中，使得BC=R的有（ ） A①② B①③ C②③ D①②③
3、如图，在⊙O中，弦EF∥直径AB，若弧AE的度数为50°，则 弧BF的度数为 50° ，弧EF的度数为 80°，∠EOF= 80° ， ∠EFO= 50° 。 弦AE与BF是什么关系？

归纳：圆心为O、半径为r的圆可以看成是所有到定 点O的距离等于定长r的点组成的图形．
A
r
O·
思考
为什么车轮都采用圆形，而不是三角形、正方形或其他？
把车轮做成圆形，车轮上各点到车轮中心（圆心）的距离都等于车轮的半径，当车轮在 平面上滚动时，车轮中心与平面的距离保持不变，因此，当车辆在平坦的路上行驶时，坐 车的人会感觉到非常平稳，假如车轮变了形，不成圆形了，到轴的距离不相等了，车就不 会再平稳。
➢ 圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
B
O·
B A
O·
A
与圆有关的概念（优弧和劣弧）
⌒
小于半圆的弧（如图中的 AC）叫做劣弧； ⌒ 大于半圆的弧（用三个字母表示，如图中的 ABC ）叫做优弧.
B
O·
C A
【注意】 1）弧分为是优弧、劣弧、半圆。 2）已知弧的两个起点，不能判断它是优弧还是 劣弧，需分情况讨论。
方法二
方法三
A
O·
利用图钉画圆
圆的概念
如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端 点A所形成的图形叫做圆．
➢ 固定的端点O叫做圆心 ➢ 线段OA叫做半径
➢ 以点O为圆心的圆，记作“⊙O”，读作“圆 O”．
A
r
O·
圆的特征
尝试画出一个圆，在画圆的过程中你发现了什么？ 【发现一】圆上各点到定点（圆心O）的距离都等 于定长（半径r）； 【发现二】到定点的距离等于定长的点都在同一个圆上．
直线与圆的位置关系的判定方法二：
直线l：Ax+By+C=0 圆C：(x-a)2+(y-b)2=r2(r>0) 利用圆心到直线的距离d与半径r的大小关系判断：

例题二：圆周角定理的证明
总结词
圆周角定理是圆的基本性质之一，它描述了圆上任意两个弧所对应的圆周角之间的关系 。
详细描述
首先，我们需要理解圆周角定理的内容，即“在同圆或等圆中，相等的弧所对应的圆周 角相等”。然后，我们可以通过一些例题来加深对圆周角定理的理解和应用。例如，我 们可以考虑如何利用圆周角定理来求解与圆相关的几何问题，如求圆的面积、求圆上任
圆是一种特殊的几何 图形，它由一条曲线 和圆心、半径等几何 元素组成
圆的性质
01
02
03
圆的对称性
圆是一个轴对称图形，任 何一条直径所在的直线都 是圆的对称轴
圆的旋转不变性
以圆心为固定点，圆在旋 转时形状和大小保持不变
圆的离心率
圆的离心率等于0，意味 着圆是一种特殊的椭圆
圆中的特殊点
01
02
03
04
CATALOGUE
圆的易错知识点
易错点一：概念不清
圆的基本概念：圆心、 半径、直径、弧、弦等
。
01
圆的方程：圆的标准方 程、一般方程和参数方
程。
03ቤተ መጻሕፍቲ ባይዱ
圆的性质：圆心角与弧 长、圆周角与弦长等。
05
圆的定义：平面上所有 与给定点（圆心）距离 等于给定正数（半径）
的点的集合。
02
圆与直线、圆与圆的位 置关系等。
圆与坐标系
圆与坐标系的关系
在坐标系中，可以通过给定圆的方程 来描述一个圆的位置和大小。同时， 也可以通过给定点的坐标来描述一个 点在圆上的位置。
圆与坐标系的应用
在解题中，可以利用圆与坐标系的性 质，如圆的方程、点到圆心的距离等 ，来解决一些综合题。同时，也可以 利用坐标系中的对称性来简化一些问 题。

2021/10/10
30
6．(2017·十堰)如图，△ABC内接于⊙O，∠ACB＝90°，
∠ACB的角平分线交⊙O于D.若AC＝6，BD＝5 2 ，则BC的长 为__8__．
2021/10/10
31
考点四 圆内接四边形 (5年1考) 例4 如图，△ABC为⊙O的内接三角形，∠AOB＝100°，则 ∠ACB的度数为 ．
弦CD的长为___1_4__．
2021/10/10
18
考点二 圆心角、弧、弦之间的关系 (5年2考) 例2 (2017·宁津模拟)把一张圆形纸片按如图所示方式折叠 两次后展开，图中的虚线表示折痕，则 的度数是( )
A．120° B．135° C．150° D．165°
2021/10/10
19
【分析】 直接利用翻折变换的性质、锐角三角函数关系
2021/10/10
15
在Rt△OPH中，∵∠OPH＝30°，
∴∠POH＝60°， ∴OH＝ 1 OP＝1.
2
在Rt△OHC中，∵OC＝4，OH＝1，
2021/10/10
16
讲：
利用辅助线求解垂径定理问题
在与圆有关的题目中，涉及弦时，一般先作辅助线，
构造垂径定理的应用环境．最易触雷的地方是不会作辅助
得出∠BOC的度数，再利用弧度与圆心角的关系得出答案．
【自主解答】 如图，连接BO，过点O作OE⊥AB于点E，
由题意可得EO＝ 1 BO，AB∥DC，
2
∴∠EBO＝30°，故∠BOD＝30°，
则∠BOC＝150°，
故 的度数是150°.故选C.
2021/10/10
20
3．如图，⊙O经过五边形OABCD的四个顶点，若∠AOD＝ 150°，∠A＝65°，∠D＝60°，则 的度数为__4_0_°_．

(C)3 cm
(D)2 cm
1 1 CD= ×8=4 cm. 2 2
3 ,E是 AB 的中点,求DE的长. 5
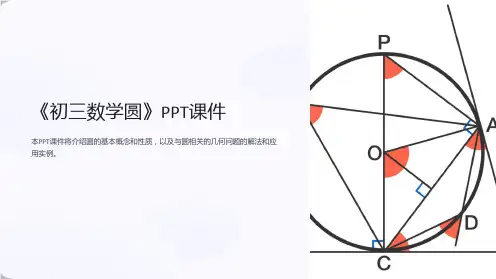
思路点拨:(2)过点 A 作 AM⊥DE,由圆内接四边形的性质可得∠ CFD=∠B=∠C,则 DC=DF=DB=6 cm,由 E 是 AB 的中点得∠ADE=45°,先解 Rt△ABD 求出 AD,再解 Rt △ADM 求出 AM 和 DM,最后解 Rt△AEM 求出 EM,即可得解.
4.圆周角和圆心角的关系
一条弧所对的圆周角等于它所对的圆心角的 的圆周角相等;半圆(或直径)所对的圆周角是
一半 ,在同圆或等圆中,同弧或等弧所对 直角 ,90°的圆周角所对的弦是直径.
5.圆内接四边形 (1)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆 外接 个圆叫这个多边形的 圆. 互补 (2)圆内接四边形的对角 . 内接 多边形,这
模块六 第21讲
圆的有关概念
圆
圆的有关概念及性质
1.圆:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的 半径 图形叫做圆.其固定的端点O叫做 圆心 ,线段OA叫做 . 2.弦:连接圆上任意两点的 线段 . 劣弧 . 3.弧:圆上任意两点间的部分.大于半圆的弧叫 优弧 ,小于半圆的弧叫 相等 4.等圆:能够 重合 的两个圆叫做等圆,同圆或等圆的半径 . 5.等弧:在同圆或等圆中,能够 重合 的弧.
圆的有关性质(常考点) 1.圆是轴对称图形,任何一条 直径 所在的直线都是圆的对称轴,圆既是中心对称图形,
又是旋转对称图形,即旋转任意角度都和自身重合.圆心就是它的对称中心.
2.垂径定理及其推论
(1)垂径定理:垂直于弦的直径 平分弦,并且平分弦所对的两条弧.