习题课3.静定平面桁架的内力计算

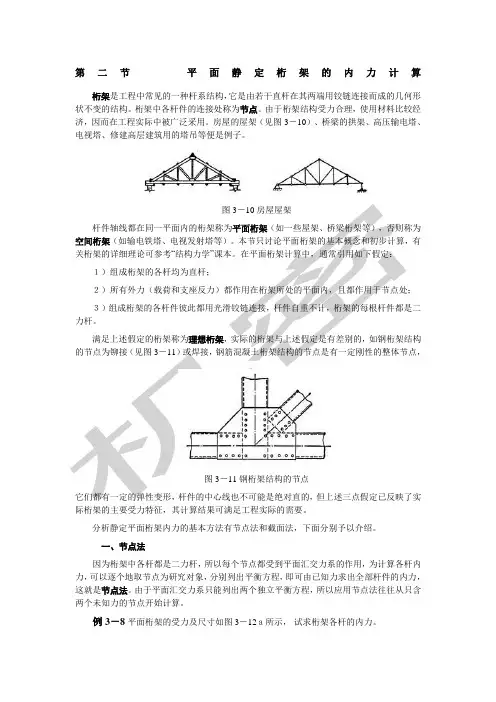
第二节平面静定桁架的内力计算桁架是工程中常见的一种杆系结构，它是由若干直杆在其两端用铰链连接而成的几何形状不变的结构。

桁架中各杆件的连接处称为节点。

由于桁架结构受力合理，使用材料比较经济，因而在工程实际中被广泛采用。

房屋的屋架（见图3－10）、桥梁的拱架、高压输电塔、电视塔、修建高层建筑用的塔吊等便是例子。

图3－10房屋屋架杆件轴线都在同一平面内的桁架称为平面桁架（如一些屋架、桥梁桁架等），否则称为空间桁架（如输电铁塔、电视发射塔等）。

本节只讨论平面桁架的基本概念和初步计算，有关桁架的详细理论可参考“结构力学”课本。

在平面桁架计算中，通常引用如下假定：１）组成桁架的各杆均为直杆；２）所有外力（载荷和支座反力）都作用在桁架所处的平面内，且都作用于节点处；３）组成桁架的各杆件彼此都用光滑铰链连接，杆件自重不计，桁架的每根杆件都是二力杆。

满足上述假定的桁架称为理想桁架，实际的桁架与上述假定是有差别的，如钢桁架结构的节点为铆接（见图3－11）或焊接，钢筋混凝土桁架结构的节点是有一定刚性的整体节点，图3－11 钢桁架结构的节点它们都有一定的弹性变形，杆件的中心线也不可能是绝对直的，但上述三点假定已反映了实际桁架的主要受力特征，其计算结果可满足工程实际的需要。

分析静定平面桁架内力的基本方法有节点法和截面法，下面分别予以介绍。

一、节点法因为桁架中各杆都是二力杆，所以每个节点都受到平面汇交力系的作用，为计算各杆内力，可以逐个地取节点为研究对象，分别列出平衡方程，即可由已知力求出全部杆件的内力，这就是节点法。

由于平面汇交力系只能列出两个独立平衡方程，所以应用节点法往往从只含两个未知力的节点开始计算。

例3－8 平面桁架的受力及尺寸如图3－12ａ所示，试求桁架各杆的内力。

图3－12 例3－8图解：（1）求桁架的支座反力以整体桁架为研究对象，桁架受主动力2F以及约束反力、、作用，列平衡方程并求解：，＝０，２×－＝０，＝，＋－２＝０，＝2－=（2）求各杆件的内力设各杆均承受拉力，若计算结果为负，表示杆实际受压力。

1、杆系结构中梁、刚架、桁架及拱的分类，是根据结构计算简图来划分的。

(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。

(错误)3静力和动力荷载的区别，主要是取决于它随时间变化规律、加载速度的快慢。

其定性指标由结构的自振周期来确定。

(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动，(正确)又不能相对转动。

(错误)5、线弹性结构是指其平衡方程是线性的，(正确)变形微小，(正确)且应力与应变之间服从虎克定律。

(正确)1、学习本课程的主要任务是：研究结构在各种外因作用下结构内力与（）计算，荷载作用下的结构反应；研究结构的（）规则和（）形式等问题。

正确答案：位移，动，组成，合理2、支座计算简图可分为刚性支座与弹性支座，其中刚性支座又可分为（）、（）、（）和（）。

正确答案：链杆，固定铰支座，固定支座，滑动支座3、永远作用在结构上的荷载称为固定荷载，暂时作用在结构上的荷载称为（）它包括（）、（）、（）、（）和（）等正确答案：活载，风，雪，人群，车辆，吊车4、刚节点的特性是被连接的杆件载连接处既无（）又不能相对（）；既可传递（），也可传递（）正确答案：移动，转动，力，力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。

（）O正确答案：正确2、两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。

（）正确答案：正确3、在图示体系中，去掉1-5，3-5，4-5，2-5，四根链杆后，的简支梁12，故该体系具有四个多余约束的几何不变体系。

（）12345正确答案：错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。

（）正确答案：错误5、图示体系是几何不变体系。

()正确答案：错误2-2几何组成分析1．正确答案：几何不变，且无多余联系。

2．(图中未编号的点为交叉点。

)A B CDEF正确答案：铰接三角形BCD视为刚片I，AE视为刚片II，基础视为刚片III；I、II间用链杆AB、EC构成的虚铰(在C点)相连，I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联，II、III 间由链杆AF和E处支杆构成的虚铰相联3．(图中未画圈的点为交叉点。

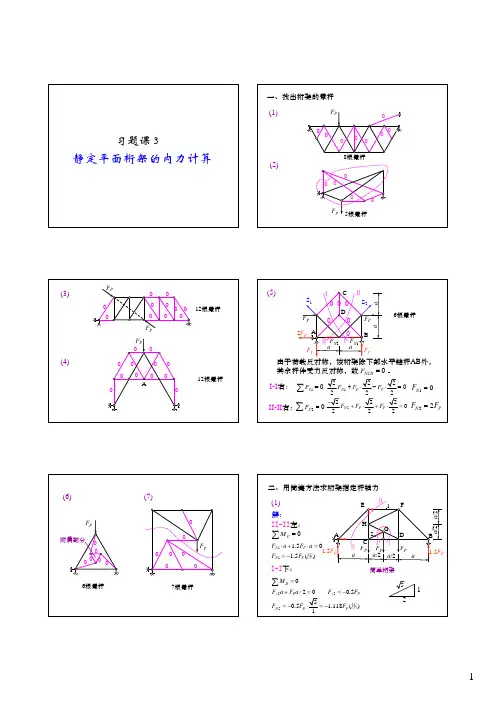
习题课3静定平面桁架的内力计算一、找出桁架的零杆(1)F P000000(2)8根零杆5根零杆F P000(3)12根零杆F PF P 00000000000F P 12根零杆(4)A 000000000006根零杆(5)a aaaS 1S 2F P 2F P F P F N 2F N 1AB C DⅡⅡⅠⅠ00000由于荷载反对称，该桁架除下部水平链杆AB 外，其余杆件受力反对称，故。

0=NCD F 1S F=∑I-I 右：20S F =∑II-II 右：12220222N P P F F F +⋅−⋅=10N F =22220222N P P F F F −+⋅+⋅=22N P F F =F PF P(7)(6)F P0附属部分6根零杆7根零杆F P0000000二、用简捷方法求桁架指定杆轴力150+II-II 左：(1)ABC DE FGHa /2a /2ⅡⅡⅠⅠ12解：CM=∑11 1.51.5()N P N P F a F a F F ⋅⋅==−压220/200.5Dy P y PMF a F a F F =+==−∑I-I 下：250.5 1.118()1N P P F F F =−⋅=−压简单桁架1.5F PF P F P F Pa a /2aa /2 1.5F P125(2)F NF yB =2F P dd dd F PAC DB dⅡⅡⅠⅠ1F yC =F PF yA =F PF xA =2F P 323F P2F P331)020()2)0()3)0()C N P P N P x N P y yC P M F d F d F d F F F F F F F F =+−======↑∑∑∑拉拉I-I 右：联合桁架解：F NF yB =2F P dd ddF PAC DB dⅡⅡⅠⅠ1F yC =F PF yA =F PF xA =2F P 323F P2F P1210()()032()D N P P yN P P P M F F d F dF F F F F ==−⋅=−==−=−∑∑压压II-II 左：整体平衡：10(322)()2ByA P P P P P MF F d F d F d F d F d==+⋅−−=↑∑(3)F P0A -F P-F P-F PF DEC 12F PF PPF 2F N F Pa /2aⅠⅠ00B 0EN MF ==∑1)I-I 右：02=N F 2)结点C ：1102()yy PN P FF F F F ===∑拉3)结点F ：aa /2aa /2联合桁架解：(4)F P 4m4mF P F P F P 4F P6.67F P6.67F P AB FC F N 2134ⅡⅠEⅡD GH 4m4m3m3mⅠ解：1220()0()33DN P xN P MF F FF F ====−∑∑拉压1) I-I 右：2) 结点E ：2222550()346xx PN x P FF F F F F ====∑拉简单桁架F PF N 2E 23PF F P 4m4mF P F P F P 4F P6.67F P6.67F P AB FC F N 2134ⅡⅠEⅡD G H4m4m3m3mⅠ553434343x Py P PN F F F F F F ==⋅==4) 结点D ：F PFN 3F N 5D2F P2F P /3410(48)2()6F N P P P M F F F F −==+=−∑压3) II-II 右：xF=∑(5)F PCA B dⅠ1 1.5F P 1.5F P02F P F Pd 0复杂桁架1)结点C：结构与荷载均对称，两斜杆轴力为零。

静定平面桁架一、概述1．桁架的组成和特点所谓桁架是指各个杆件的两端按一定方式互相联结组成的一种结构，如钢筋混凝土屋架、施工中用的脚手架等。

当组成桁架的各杆的轴线和外力都在同一个平面时，称为平面桁架。

当平面桁架的支座反力与杆件的内力仅仅凭借平衡方程就能全部解出来，称为静定平面桁架。

如图所示，在桁架中，杆件相互联结的地方称为结点。

桁架的杆件，由于所在位置不同，可分为弦杆和腹杆。

弦杆又分为上弦杆和下弦杆，腹杆又分为竖杆和斜杆。

弦杆上两相邻的结点的区间称为节间，其距离d 称为节间长度，两支座之间的距离l 称为桁架的跨度，两支座的连线到桁架最高点之间的垂直距离H 称为桁高。

上弦杆图11.10图工程中实际的桁架，如钢筋混凝土桁架和钢桁架，各结点做成后，一般具有刚性，而且各杆轴线也不一定都交于一点，所以按照实际的桁架进行内力分析计算比较困难。

但从桁架的实际工作情况、计算分析和模型实际的结果来看，各杆件主要承受轴力，而弯 矩和剪力则很小，可以忽略不计。

因此，为了简化计算，通常采用如下假定： （1）各结点都是光滑的铰结点。

（2）各杆轴都是直线，并都在同一平面内且通过铰的中心。

（3）荷载和支座反力，都作用在结点上，并位于桁架的平面内。

通常把符合上述假定的桁架称为理想平面桁架。

桁架多用钢材、木材或钢筋混凝土制作，在桥梁、房建和水工等结构中广泛应用。

实际的桁架一般并不完全符合上述理想桁架的假定（如图）。

例如，结点具有一定的刚性，有些杆件在结点处可能是连续的，并没有断开；各杆轴线无法绝对平直，结点上各杆的轴线也不一定完全交于一点；荷载不一定都作用在结点上，等等。

因此，实际桁架在荷载作用下，杆件将产生弯曲应力，并不像理想条件下只产生均匀分布的轴向应力。

但科学实验和工程实践表明，结点刚性等因素对桁架内力的影响一般说来是次要的。

因此，可以将图（a ）简化为如图（b ）所示的计算简图。

按照这种计算简图所求得的内力称为桁架的主内力。

桁架内力的计算3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点，熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。

这种结构形式在桥梁和房屋建筑中应用较为广泛，如南京长江大桥、钢木屋架等。

实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的，实际受力情况复杂，要对它们进行精确的分析是困难的。

但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明，由于大多数的常用桁架是由比较细长的杆件所组成，而且承受的荷载大多数都是通过其它杆件传到结点上，这就使得桁架结点的刚性对杆件内力的影响可以大大的减小，接近于铰的作用，结构中所有的杆件在荷载作用下，主要承受轴向力，而弯矩和剪力很小，可以忽略不计。

因此，为了简化计算，在取桁架的计算简图时，作如下三个方面的假定：（1）桁架的结点都是光滑的铰结点。

（2）各杆的轴线都是直线并通过铰的中心。

（3）荷载和支座反力都作用在铰结点上。

通常把符合上述假定条件的桁架称为理想桁架。

3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。

因此，桁架中的所有杆件均为二力杆。

在杆的截面上只有轴力。

3.4.1.3 桁架的分类（1）简单桁架：由基础或一个基本铰接三角形开始，逐次增加二元体所组成的几何不变体。

（图3-14a）（2）联合桁架：由几个简单桁架联合组成的几何不变的铰接体系。

（图3-14b）（3）复杂桁架：不属于前两类的桁架。

（图3-14c）3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为：结点法、截面法、联合法结点法――适用于计算简单桁架。

截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。

联合法――在解决一些复杂的桁架时，单独应用结点法或截面法往往不能够求解结构的内力，这时需要将这两种方法进行联合应用，从而进行解题。

解题的关键是从几何构造分析着手，利用结点单杆、截面单杆的特点，使问题可解。