偏倚和线性

MSA测量系统分析MSA（测量系统分析）是一种用于评估和改进测量系统稳定性、偏倚和线性性能的方法。

通过进行MSA，可以确定测量系统是否足够稳定和准确，以便在不同的情况下对产品进行正确的测量。

稳定性是指测量系统在相同的测量条件下的一系列测量结果是否一致。

稳定性是MSA中最基本的指标之一，因为如果测量系统不稳定，那么无论多么准确的测量工具都无法提供可靠的测量结果。

偏差是指测量结果与真实值之间的差异。

在MSA中，需要比较测量系统的平均偏差与零偏差之间的差异。

如果两者之间存在较大的差异，则说明测量系统存在系统性的偏离问题，需要进行校准或修正。

线性是指测量系统的输出是否与输入之间存在良好的线性关系。

在MSA中，需要绘制出测量系统的线性回归图，通过斜率和截距来评估测量系统的线性性能。

如果回归线接近理想的45度直线，则说明测量系统的线性性能较好。

在进行MSA时，一般采用以下步骤来评估测量系统的稳定性、偏差和线性性能：1.收集测量数据：使用相同的测量系统对一批样本进行测量，并记录测量结果。

2.统计分析：对于每个样本，计算测量结果的平均值和标准偏差。

然后，计算每个样本平均值之间的差异，并计算整体平均偏差和标准偏差。

3. 制作控制图：使用收集的测量结果，绘制测量系统稳定性的控制图。

通常使用X-bar图来监控平均值的稳定性，使用R或S图来监控标准偏差的稳定性。

4.比较平均偏差和零偏差：计算测量系统的平均偏差和零偏差之间的差异，并进行比较。

如果差异较大，则说明测量系统存在系统性的偏离问题。

5.绘制线性回归图：使用测量数据，绘制测量系统的线性回归图。

计算斜率和截距，并与理想的45度直线进行比较。

如果回归线接近理想线，则说明测量系统具有良好的线性性能。

通过以上步骤，可以对测量系统进行全面的评估，并确定是否需要采取措施来改善测量系统的稳定性、偏差和线性性能。

常用的改善方法包括校准测量工具、调整测量程序和培训操作人员等。

总之，MSA是一种重要的质量管理工具，能够帮助企业评估和改进测量系统的稳定性、偏差和线性性能。

MSA（MeasurementSystemAnalysis）使用数理统计和图表的方法对测量系统的分辨率和误差进行分析，以评估测量系统的分辨率和误差对于被测量的参数来说是否合适，并确定测量系统误差的主要成分。

以事实和数据驱动管理，而数据是测量的结果，因此在开展统计分析时，要特别强调数据本省的质量和相应的测量系统分析。

测量：是指对具体事物赋予数值，以表示它们与特定特性之间的关系。

在这个过程中，由人员、仪器或量具、测量对象、操作方法和环境构成的整体就是测量系统。

所谓测量系统分析，是指运用统计学的方法对测量系统进行评估，在合适的特性位置测量正确的参数，了解影响测量结果的波动来源及分布，并确认测量系统是否符合工程需求。

任何实测数据的波动都可以看作过程的波动和测量系统的波动之和，即σ2总=σ2过程+σ2测量系统六个常见的测量系统评估项目稳定性、偏倚、线性、分辨率、重复性和再现性。

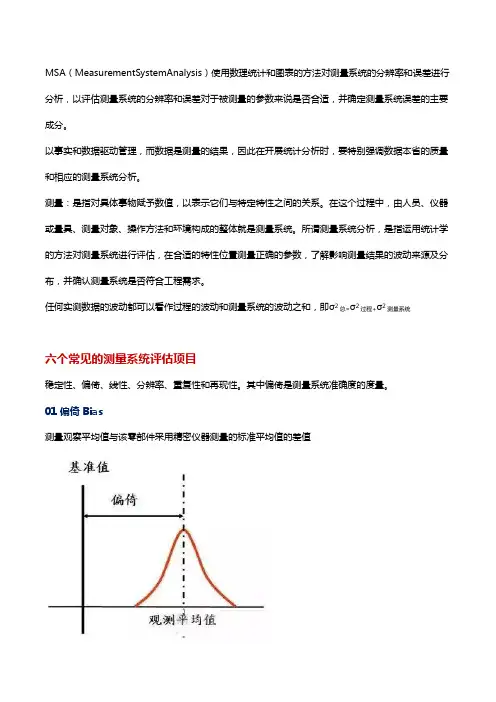
其中偏倚是测量系统准确度的度量。

01偏倚Bias测量观察平均值与该零部件采用精密仪器测量的标准平均值的差值02线性表征量具预期工作范围内偏倚值的差别03稳定性表征测量系统对于给定的零部件或标准件随时间变化系统偏倚中的总偏差量，与通常意义上的统计稳定性是有区别的04重复性指同一个评价人，采用同一种测量仪器，多次测量同一零件的同一特性时获得的测量值（数据）的偏差05再现性指由不同的评价人，采用相同的测量仪器，测量同一零件的同一特性时测量平均值的偏差通常，前三种指标用于评价测量系统的准确性，后两种指标用于评价测量系统的精确性。

测量系统的准确性可以通过对设备的校准等对测量系统进行维护、监控，也就是说，通过对测量系统的分辨率、偏倚、线性和稳定性进行分析后进行校准后可以解决其准确性问题。

工程上通常用测量系统的精确性也就是其重复性和再现性来研究其统计特性，就是通常所说的“GR&R研究”。

测量系统分析流程及方法测量系统分析是一项重要的系统工程。

线性偏倚研究报告解读线性偏倚研究报告解读引言在统计学和机器学习中，线性偏倚是一个重要的概念。

它指的是在使用线性模型对数据进行拟合时，模型的输出与真实值之间存在一定的偏差。

本文将解读一份研究报告，其中探讨了线性偏倚的性质以及可能的影响。

研究背景线性偏倚是机器学习领域的一个热门研究方向，因为它在实际应用中经常出现，并且可能会导致模型的性能下降。

了解线性偏倚的性质和来源，可以帮助我们更好地理解模型的表现和改进模型的拟合能力。

研究目的本研究的目的是探究线性偏倚的性质，并通过实验验证一些假设。

通过对研究结果的解读，我们可以更好地了解线性偏倚对模型性能的影响，并提出可能的解决方案。

研究方法本次研究采用了以下方法来对线性偏倚进行分析。

数据收集研究者使用了一个包含1000个样本的数据集，每个样本包含多个特征和一个目标变量。

这些样本是通过调查问卷收集而来，涵盖了不同年龄、性别和收入水平的人群。

线性拟合研究者使用了线性回归模型对数据进行拟合。

他们选择了一组特征作为自变量，并将目标变量作为因变量，使用最小二乘法求解最佳参数。

偏差分析在拟合模型后，研究者进行了偏差分析。

他们比较了模型预测值与真实值之间的差异，并计算了平均偏差和方差。

此外，他们还通过绘制残差图和残差分布图来可视化偏差的分布情况。

影响因素探索在分析偏差的性质后，研究者进一步探索了可能的影响因素。

他们使用了模型解释方法来计算每个特征对目标变量的贡献程度，并分析了特征与偏差之间的相关性。

结果与讨论偏差的性质根据研究结果，线性偏倚在该数据集中普遍存在。

模型的预测值整体上偏离了真实值，表现出了一定的系统性偏差。

平均偏差为0.2，方差为0.1，说明模型对部分样本的预测结果相对稳定，但对另一部分样本的预测结果变化较大。

偏差的分布通过绘制残差图和残差分布图，我们可以观察到偏差的分布情况。

图中显示，偏差的分布大致呈正态分布，但在一些特定范围内偏差较大。

这可能是由于数据特征的分布不均匀或模型无法很好地拟合某些关键特征。

一、测量系统分析在日常生产中，我们经常根据获得的过程加工部件的测量数据去分析过程的状态、过程的能力和监控过程的变化；我们必须从两方面来保证分析的结果是正确的，一是确保测量数据的准确性/质量，使用MSA方法对获得测量数据的测量系统进行评估；二是确保使用了合适的数据分析方法，如使用SPC工具、试验设计、方差分析、回归分析等。

测量系统的误差由稳定条件下运行的测量系统多次测量数据的统计特性：偏倚和方差来表征。

偏倚指测量数据相对于标准值的位置，包括测量系统的偏倚（Bias）、线性（Linearity）和稳定性（Stability）；而方差指测量数据的分散程度，也称为测量系统的R&R，包括测量系统的重复性（Repeatability）和再现性（Reproducibility）。

一般来说，测量系统的分辨率应为获得测量参数的过程变差的十分之一。

测量系统的偏倚和线性由量具校准来确定。

测量系统的稳定性可由重复测量相同部件的同一质量特性的均值极差控制图来监控。

测量系统的重复性和再现性由GageR&R研究来确定。

分析用的数据必须来自具有合适分辨率和测量系统误差的测量系统，否则，不管我们采用什么样的分析方法，最终都可能导致错误的分析结果。

在ISO10012-2和QS9000中，都对测量系统的质量保证作出了相应的要求，要求企业有相关的程序来对测量系统的有效性进行验证。

测量系统特性类别有F、S级别，另外其评价方法有小样法、双性、线性等.分析工具在进行MSA分析时，推荐使用Minitab软件来分析变异源并计算Gage R&R和P/T。

并且根据测量部件的特性，可以对交叉型和嵌套型部件分别做测量系统分析。

当一个部件只被一个测量员测量一次，其获得的数据模型就是嵌套模型；如果被多个测量员重复多次测量，其获得的数据模型就是交叉模型，而原则上，如果部件条件允许时，部件应该被多个测量员重复测量，以评估测量系统的再现性和重复性变差。

这个话题如果没有实践的人一定是弄不清楚的,就算是有实践的人也未必能弄清楚,因为他们的相互交错.福特用了一百年的时间画出了经典的APQP网络图,可见其用心之最.在这里我对五大工具做简单的描述希望能给大家一个基本的概念.APQP是在整车厂提供新产品品的时候,做为零部件公司必须要做的一项工作,意在在产品未进行生产之前把所有的问题解决掉,所以它是个复杂的过程,也是需要几个来回反复才会成为最后策划的结果.FMEA则是在APQP的二三阶段时进行的失效模式分析,包括产品和过程,这里最重要的一点是这个时候产品并未生产出来,而是一种潜在的可能性分析,很多企业总是不习惯这一点,总是把它当成已经在生产的产品去分析.SPS,MSA都是在对过程策划的过程中形成的东西,也就是说什么样的过程需要用SPC来控制,一般来说具有特殊特性的过程应该用SPC,当然也不是绝对.这里需要说明的是控制计划,是APQP策划的结果,在这个结果中必然要用到测量工具,而这些测量工具是否能满足对过程测量的需要,需要用MSA来进行分析,简单地说控制计划中所涉及的测量器具都应该做MSA,然后在最初的控制计划中,也就是试生产的控制计划中,策划的测量工具或所选用的SPC未必能有好的效果,因些可能会进行调整和改进,最后形成正式生产的控制计划.而正式生产控制计划中的SPC和MSA应该是能满足批量生产的需要.简单地说：APQP是质量计划，但其实也是项目开发的计划。

既然是计划，它的时间起点是项目正式启动的那一时间点到PPAP结束，正常量产后进行总结，认为没有其他问题，可以关闭开发项目的那一时间点为止。

执行人是整个APQP小组。

PPAP是生产件批准程序，只是整个APQP 计划中的一个环节，通常居于APQP计划的后半阶段，一般来讲是APQP计划的核心。

若PPAP没有获得客户的批准，那么APQP的计划基本要泡汤。

因此我们谈论起APQP，总是把它们说在一起：APQP/PPAP。

测量系统分析（MSA）测量系统分析（MSA）1目得与范围规范测量系统分析，明确实施方法、步骤及对数据得处理、分析。

2规范性引用文件无3定义3.1测量系统：用来对测量单元进行量化或对被测得特性进行评估，其所使用得仪器或量具、标准、操作、方法、夹具、软件、人员、环境及假设得集合；也就就是说，用来获得测量结果得整个过程。

3.2稳定性：就是测量系统在某持续时间内测量同一基准或零件得单一特性时获得得测量值总变差。

稳定性就是整个时间得偏倚得变化。

3.3分辨率：为测量仪器能够读取得最小测量单位。

别名：最小读数单位、刻度限度、或探测度、分辨力；要求低于过程变差或允许偏差（tolerance）得十分之一。

Minitab中常用得分辨率指标：可区分得类别数ndc=(零件得标准偏差/ 总得量具偏差)* 1、41，一般要求它大于等于5才可接受，10以上更理想。

3.4过程总波动TV=6σ。

σ——过程总得标准差3.5准确性（准确度）：测量得平均值就是否偏离了真值，一般通过量具计量鉴定或校准来保证。

3.5.1真值：理论正确值，又称为：参考值。

3.5.2偏倚：就是指对相同零件上同一特性得观测平均值与真值得差异。

%偏倚=偏倚得平均绝对值/TV。

3.5.3线性：在测量设备预期得工作量程内，偏倚值得差值。

用线性度、线性百分率表示。

3.6精确性（精密度）：测量数据得波动。

测量系统分析得重点，包括：重复性与再现性3.6.1重复性：就是由一个评价人，采用一种测量仪器，多次测量同一零件得同一特性时获得得测量值变差。

重复性又被称为设备波动（equipment variation，EV）。

3.6.2再现性：就是由不同得评价人，采用相同得测量仪器，测量同一零件得同一特性时测量平均值得变差。

再现性又被称为“评价人之间”得波动（appraiser waration，AV）。

3.6.3精确性%公差（SV/Toler），又称为%P/T：就是测量系统得重复性与再现性波动与被测对象质量σ/ (USL-LSL) *100%。