浓度问题之十字交叉法
- 格式:doc
- 大小:95.50 KB
- 文档页数:12

十字交叉法解浓度问题十字交叉法是解决溶液浓度问题的一种简单有效的方法,通常用于计算不同浓度的液体或溶液的混合比例。
该方法基于比例关系,将给定的溶液容量、浓度和所需混合后的溶液浓度进行杂交,以找到所需的混合比例。
下面将介绍十字交叉法解浓度问题的具体步骤。
步骤一:确定所需的混合溶液浓度和容量首先需要确定目标混合溶液的浓度和容量。
这可以根据具体的实验要求或应用场景进行选择。
例如,如果需要制备100mL的20%浓度的溶液,那么这些信息需要在问题中明确给出。
步骤二:将浓度和容量写成比例式根据比例关系,将目标混合溶液的浓度和容量写成比例式,如下所示:目标溶液浓度/100 = X(所需体积)/与该浓度液体混合的体积例如,对于要制备100mL的20%溶液,可以写成:20/100 = X / (100 - X)其中,X代表所需体积,100-X代表与该浓度液体混合的体积。
步骤三:根据已知条件解出所需的体积将已知条件代入比例式中,解出所需的体积。
以制备100mL的20%溶液为例,可进行以下计算:20/100 = X / (100 - X)化简后得到X = 20mL通过这个比例式,可以得出制备20%浓度的溶液,需要取20mL的纯化液加入80mL的稀释液中。
步骤四:计算所需的纯化液体积根据已知条件和所需的体积,可以计算出所需的纯化液体积。
对于上面的例子,需要取20mL的纯化液体,所以所需的纯化液体积即为20mL。
步骤五:计算所需的稀释液体积最后,开始计算所需的稀释液体积。
根据上面的例子,所需的总体积为100mL,其中20mL是纯化液体,所以所需的稀释液体积为80mL。
通过上述五个步骤,就可以利用十字交叉法解决浓度问题。
需要注意的是,在计算过程中,必须确保所使用的所有单位都是相同的,并且需要对计算结果进行检查,确保其正确无误。
总结十字交叉法是解决浓度问题的一种简单而有效的方法,它可以用于计算不同浓度的液体或溶液的混合比例。

浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口张贴着广告:“既甜又浓的豆浆每杯0.3元。
”黑熊便招呼弟弟们歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,加满水后给老三喝掉了31,再加满水后,又给老二喝了一半,最后自己把剩下的一半喝完。
狐狸开始收钱了,他要求黑熊最小的弟弟付出0.3×61=0.05(元);老三0.3×31=0.1(元);老二与黑熊付的一样多,0.3×21=0.15(元)。
兄弟一共付了0.45元。
兄弟们很惊讶,不是说,一杯豆浆0.3元,为什么多付0.45-0.3=0.15元?肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
”“不给,休想离开。
”现在,说说为什么会这样呢?专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量溶液质量×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。

、一、十字交叉法十字交叉法是数算里面的一个重要方法,很多比例问题,都可以用十字交叉法来很快地解决,而在资料分析中,也能够派上很大用场,所以应该认真掌握它。
(一)原理介绍通过一个例题来说明原理。
例:某班学生的平均成绩是80分,其中男生的平均成绩是75,女生的平均成绩是85。
求该班男生和女生的比例。
方法一:男生一人,女生一人,总分160分,平均分80分。
男生和女生的比例是1:1。
方法二:假设男生有A,女生有B。
(A*75+B85)/(A+B)=80整理后A=B,因此男生和女生的比例是1:1。
方法三:男生:75 580女生:85 5男生:女生=1:1。
一个集合中的个体,只有2个不同的取值,部分个体取值为A,剩余部分取值为B。
平均值为C。
求取值为A的个体与取值为B的个体的比例。
假设A有X,B有(1-X)。
AX+B(1-X)=CX=(C-B)/(A-B)1-X=(A-C)/(A-B)因此:X:(1-X)=(C-B):(A-C)上面的计算过程可以抽象为:A C-BCB A-C这就是所谓的十字相乘法。
十字相乘法使用时要注意几点:第一点:用来解决两者之间的比例关系问题。
第二点:得出的比例关系是基数的比例关系。
第三点:总均值放中央,对角线上,大数减小数,结果放对角线上。
(二)例题与解析1.某体育训练中心,教练员中男占90%,运动员中男占80%,在教练员和运动员中男占82%,教练员与运动员人数之比是A.2:5 B.1:3 C.1:4 D.1:5答案:C 分析:男教练:90% 2%82%男运动员:80% 8%男教练:男运动员=2%:8%=1:42.某公司职员25人,每季度共发放劳保费用15000元,已知每个男职必每季度发580元,每个女职员比每个男职员每季度多发50元,该公司男女职员之比是多少A.2∶1 B.3∶2 C. 2∶3 D.1∶2答案:B分析:职工平均工资15000/25=600男职工工资:580 30600女职工工资:630 20男职工:女职工=30:20=3:23.某城市现在有70万人口,如果5年后城镇人口增加4%,农村人口增加5.4%,则全市人口将增加4.8%。


数学运算--浓度问题和十字交叉法数学运算--浓度问题和十字交叉法从本质上来说,浓度问题就是指溶液的浓度变化问题。
要解决浓度问题,我们首先要了解溶液、溶剂、溶质和浓度的关系。
溶液、溶剂、溶质和浓度的关系如下∶•溶液的质量=溶质的质量+溶剂的质量•浓度=溶质质量÷溶液质量•溶液质量=溶质质量÷浓度•溶质质量=溶液质量×浓度难度较低的溶液问题只要通过以上几个公式就可以列方程求解,而对于一些较复杂的浓度问题,就要通过“十字交叉法”来求解。
十字交叉法是进行二组分混合物平均量与组分量的计算中常用的一种简便方法。
凡是一般的二元一次方程组(Aa +Bb = c( A +B )关系式)的习题,均可用十字交叉法。
该法解题的关键是准确找出平均值。
其解题原理为:Aa+Bb=(A+B)×c整理变形后可得 (a>c>b)其中c为平均值十字相乘法使用时要注意几点:第一点:用来解决两者之间的比例关系问题。
第二点:得出的比例关系是基数的比例关系。
第三点:总均值放中央,对角线上,大数减小数,结果放对角线上。
我们可以通过一个例题来详细了解:【例1】甲杯中有浓度17%的溶液400克,乙杯中有浓度为23%的同种溶液600克,现在从甲,乙取出相同质量的溶液,把甲杯取出的倒入乙杯中,把乙杯取出的倒入甲杯中,使甲,乙两杯溶液的浓度相同,问现在两杯溶液浓度是多少?解:17% 2.4 400 2X :23% 3.6 600 3左面列纵向做差,23-17=6,把6按照2:3来分,分成2.4和3.6,则求出x=20.6%。
【例2】浓度为70%的酒精浓液100克与浓度为20%的酒精浓液400克混合后得到的浓液的浓度是多少?()A、30%B、32%C、40%D、45%【解析】A。
用十字交叉法解决:设混合后浓液的浓度为:X%溶液1:70 X-20 100X浓液2:20 70-X 400因此:X-20/70-X=100/400 推出X=30。

浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口张贴着广告:“既甜又浓的豆浆每杯0.3元。
”黑熊便招呼弟弟们歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,加满水后给老三喝掉了31,再加满水后,又给老二喝了一半,最后自己把剩下的一半喝完。
狐狸开始收钱了,他要求黑熊最小的弟弟付出0.3×61=0.05(元);老三0.3×31=0.1(元);老二与黑熊付的一样多,0.3×21=0.15(元)。
兄弟一共付了0.45元。
兄弟们很惊讶,不是说,一杯豆浆0.3元,为什么多付0.45-0.3=0.15元?肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
”“不给,休想离开。
”现在,说说为什么会这样呢?专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=\F(溶质质量,溶液质量) ×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。

一、十字交叉法十字交叉法是数算里面的一个重要方法,很多比例问题,都可以用十字交叉法来很快地解决,而在资料分析中,也能够派上很大用场,所以应该认真掌握它。
(一)原理介绍通过一个例题来说明原理。
例:某班学生的平均成绩是80分,其中男生的平均成绩是75,女生的平均成绩是85。
求该班男生和女生的比例。
方法一:男生一人,女生一人,总分160分,平均分80分。
男生和女生的比例是1:1。
方法二:假设男生有A,女生有B。
(A*75+B85)/(A+B)=80整理后A=B,因此男生和女生的比例是1:1。
方法三:男生:75 580女生:85 5男生:女生=1:1。
一个集合中的个体,只有2个不同的取值,部分个体取值为A,剩余部分取值为B。
平均值为C。
求取值为A的个体与取值为B的个体的比例。
假设A有X,B有(1-X)。
AX+B(1-X)=CX=(C-B)/(A-B)1-X=(A-C)/(A-B)因此:X:(1-X)=(C-B):(A-C)上面的计算过程可以抽象为:A C-BCB A-C这就是所谓的十字相乘法。
十字相乘法使用时要注意几点:第一点:用来解决两者之间的比例关系问题。
第二点:得出的比例关系是基数的比例关系。
第三点:总均值放中央,对角线上,大数减小数,结果放对角线上。
(二)例题与解析1.某体育训练中心,教练员中男占90%,运动员中男占80%,在教练员和运动员中男占82%,教练员与运动员人数之比是A.2:5 B.1:3 C.1:4 D.1:5答案:C分析:男教练:90% 2%82%男运动员:80% 8%男教练:男运动员=2%:8%=1:42.某公司职员25人,每季度共发放劳保费用15000元,已知每个男职必每季度发580元,每个女职员比每个男职员每季度多发50元,该公司男女职员之比是多少A.2∶1 B.3∶2 C. 2∶3 D.1∶2答案:B分析:职工平均工资15000/25=600男职工工资:580 30600女职工工资:630 20男职工:女职工=30:20=3:23.某城市现在有70万人口,如果5年后城镇人口增加4%,农村人口增加5.4%,则全市人口将增加4.8%。

、一、十字交叉法十字交叉法是数算里面的一个重要方法,很多比例问题,都可以用十字交叉法来很快地解决,而在资料分析中,也能够派上很大用场,所以应该认真掌握它。
(一)原理介绍通过一个例题来说明原理。
例:某班学生的平均成绩是80分,其中男生的平均成绩是75,女生的平均成绩是85。
求该班男生和女生的比例。
方法一:男生一人,女生一人,总分160分,平均分80分。
男生和女生的比例是1:1。
方法二:假设男生有A,女生有B。
(A*75+B85)/(A+B)=80整理后A=B,因此男生和女生的比例是1:1。
方法三:男生:75 580女生:85 5男生:女生=1:1。
一个集合中的个体,只有2个不同的取值,部分个体取值为A,剩余部分取值为B。
平均值为C。
求取值为A的个体与取值为B的个体的比例。
假设A有X,B有(1-X)。
AX+B(1-X)=CX=(C-B)/(A-B)1-X=(A-C)/(A-B)因此:X:(1-X)=(C-B):(A-C)上面的计算过程可以抽象为:A C-BCB A-C这就是所谓的十字相乘法。
十字相乘法使用时要注意几点:第一点:用来解决两者之间的比例关系问题。
第二点:得出的比例关系是基数的比例关系。
第三点:总均值放中央,对角线上,大数减小数,结果放对角线上。
(二)例题与解析1.某体育训练中心,教练员中男占90%,运动员中男占80%,在教练员和运动员中男占82%,教练员与运动员人数之比是A.2:5 B.1:3 C.1:4 D.1:5答案:C 分析:男教练:90% 2%82%男运动员:80% 8%男教练:男运动员=2%:8%=1:42.某公司职员25人,每季度共发放劳保费用15000元,已知每个男职必每季度发580元,每个女职员比每个男职员每季度多发50元,该公司男女职员之比是多少A.2∶1 B.3∶2 C. 2∶3 D.1∶2答案:B分析:职工平均工资15000/25=600男职工工资:580 30600女职工工资:630 20男职工:女职工=30:20=3:23.某城市现在有70万人口,如果5年后城镇人口增加4%,农村人口增加5.4%,则全市人口将增加4.8%。

浓度问题(十字交叉法)1,基本公式:溶液=溶质+溶剂 浓度=溶质/溶液一杯盐水,其中有盐5克,有水45克,那么该盐水的浓度是多少?(2003国考)一种挥发性药水,原来有一整瓶,第二天挥发后变为原来的21;第三天变为第二天的32;第四天变为第三天的43,请问第几天时药水还剩下301瓶( ) A .5天B .12天C .30天D .100天(2005湖南)在10克盐与40克水的盐水中,取出40克盐水,其中盐与水分别为( )克A .8,32B .10,30C .8,30D .10,32(2005上海)在20度时,100克水最多能溶解36克食盐。
从中取出食盐水50克,取出的溶液的浓度是多少( )A .36.0%B .18.0%C .26.5%D .72.0%浓度70%的酒精溶液100克与浓度20%的酒精溶液400克混合后的酒精溶液浓度是多少( )A .30%B .32%C .40%D .45%(2008北京)甲杯有浓度为17%的溶液400克,乙杯有浓度为23%的溶液600克,现在从甲,乙两杯中取出相同总量的溶液,把甲杯中取出的倒入乙杯中,把乙杯中取出的倒入甲杯中,使甲,乙两杯溶液的浓度相同,问现在两杯溶液的浓度是多少( )A .20%B .20.6%C .21.2%D .21.4%(2009安徽)当含盐30%的60千克盐水蒸发为含盐40%的盐水时,盐水重量为多少千克?( )A .45B .50C .55D .60(2007湖南)一个容器内有若干克盐水。
往容器内加入一些水,溶液的浓度变为3%,再加入同样多水,溶液的浓度变为2%,问第三次再加入同样多水后,溶液的浓度变为( )A .1.8%B .1.5%C .1%D .0.5%(2009国考)一种溶液,蒸发一定的水后,浓度为10%,再蒸发同样的水,浓度为12%,第三次蒸发同样多的水后,浓度变为多少( )C .16%D .15%一杯溶液浓度为5%,蒸发V 升水之后浓度变为6%,请问再蒸发2V 升的水之后浓度变为多少?( )A .7.5%B .8%C .9.6%D .10%(2008四川)木材原来的水分含量为28%,由于挥发,现在的水分含量为10%,则现在这些木材的重量是原来的( )A .50%B .60%C .70%D .80%(2008山东)两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积比为3:1,另一个瓶子中酒精与水的体积比是4:1,若把两瓶酒精溶液混合,则混合后的酒精和水的体积之比是多少?( )A .31:9B .7:2C .31:40D .20:11(2009湖南)有两只相同的大桶和一只空杯子,甲桶装牛奶,乙桶装糖水,先从甲桶内取出一杯牛奶倒入乙桶,再从乙桶取出一杯糖水和牛奶的混合倒入甲桶,问,此时甲桶内的糖水多还是乙桶内的牛奶多?( )A .无法判定B .甲桶糖水多C .乙桶牛奶多D .一样多2,多次混合问题Ⅰ型问题设盐水瓶中盐水的质量为M ,每次操作中先倒出0M 克盐水,再倒入0M 克清水,重复n 次。

浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口贴着广告:“既甜又浓的豆浆每杯0.3元。
”黑熊便招呼弟弟们歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,加满水后给老三喝掉了31,再加满水后,又给老二喝了一半,最后自己把剩下的一半喝完。
狐狸开始收钱了,他要求黑熊最小的弟弟付出0.3×61=0.05(元);老三0.3×31=0.1(元);老二与黑熊付的一样多,0.3×21=0.15(元)。
兄弟一共付了0.45元。
兄弟们很惊讶,不是说,一杯豆浆0.3元,为什么多付0.45-0.3=0.15元?肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
”“不给,休想离开。
”现在,说说为什么会这样呢?专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量溶液质量×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。
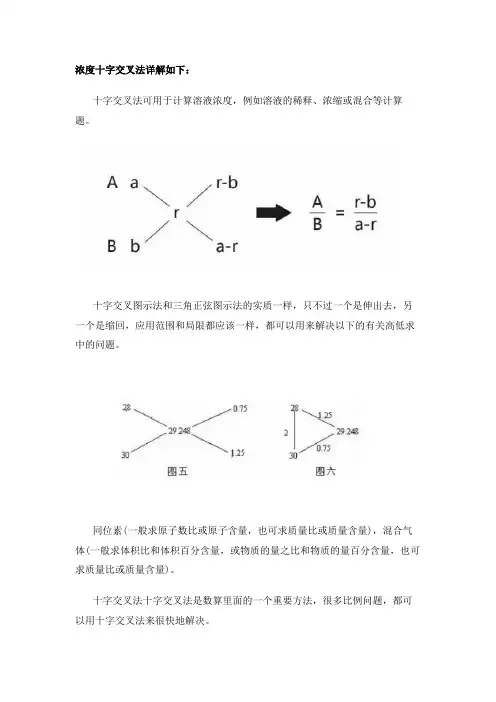
浓度十字交叉法详解如下:
十字交叉法可用于计算溶液浓度,例如溶液的稀释、浓缩或混合等计算题。
十字交叉图示法和三角正弦图示法的实质一样,只不过一个是伸出去,另一个是缩回,应用范围和局限都应该一样,都可以用来解决以下的有关高低求中的问题。
同位素(一般求原子数比或原子含量,也可求质量比或质量含量),混合气体(一般求体积比和体积百分含量,或物质的量之比和物质的量百分含量,也可求质量比或质量含量)。
十字交叉法十字交叉法是数算里面的一个重要方法,很多比例问题,都可以用十字交叉法来很快地解决。
浓度十字交叉法原理解析
浓度十字交叉法是一种用于确定化学品浓度的方法。
其原理是在量定目标物质的溶液中加入已知浓度的另一种溶液,使两种溶液混合成为等量的两个部分,然后通过对这两个部分进行化学反应或者物理检测来确定目标物质的浓度。
这个过程通常会在特定的试剂管或试剂瓶中进行,不同的试剂管或试剂瓶中含有的是不同的溶液。
浓度十字交叉法是基于两种溶液中物质浓度之间的关系来确定目标物质浓度的。
当我们将两个浓度不同的溶液混合在一起时,会得到一个新的溶液,这个新溶液的浓度是由两个溶液的浓度和混合量所决定的。
浓度十字交叉法是利用这个关系来计算目标物质的浓度。
浓度十字交叉法的计算过程通常是分为几个步骤的。
首先,我们需要确定两种溶液的浓度。
这可以通过实验室技术和化学测量仪器来完成。
然后,我们需要通过一系列试验来确定目标物质和另一种溶液之间的反应和浓度关系。
这些试验可以使用化学反应或者物理测试法来完成。
在这些试验中,我们可以通过测量溶液中化学物质的含量来确定浓度。
浓度十字交叉法在化学实验室中是一个非常重要的技术。
它可以用于确定各种化学物质的浓度,包括有机化学物质、无机化学物质和生物化学物质。
浓度十字交叉法的成功应用需要我们具有丰富的化学知识和实验技能。
只有通过不断的实验和学习,我们才能更好地掌握这一技术,并在实验中获得更准确的结果。
浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口张贴着广告:“既甜又浓的豆浆每杯元。
”黑熊便招呼弟弟们歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,加满水后给老三喝掉了31,再加满水后,又给老二喝了一半,最后自己把剩下的一半喝完。
狐狸开始收钱了,他要求黑熊最小的弟弟付出×61=(元);老三×31=(元); 老二与黑熊付的一样多,×21=(元)。
兄弟一共付了元。
兄弟们很惊讶,不是说,一杯豆浆元,为什么多付-=元肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
” “不给,休想离开。
”现在,说说为什么会这样呢 、专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量溶液质量 ×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量 溶质的重量÷溶液的重量×100%=浓度 溶液的重量×浓度=溶质的重量 溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
'浓度问题变化多,有些题目难度较大,计算也较复杂。
要根据题目的条件和问题逐一分析,也可以分步解答。
浓度问题(十指交叉法巧妙运用)如果题目中给出两个平行的情况A, B, 满足条件a, b ; 然后A和B按照某种条件混合在一起形成的情况C, 满足条件c. 而且可以表示成如下的表达式. 那么这个时候就可以用十字交叉法.判断式: A×a+B×b=(A+B)×c=C×c用十字交叉法表示:(一)基本知识点:1、溶液=溶质+溶剂;2、浓度=溶质/溶液;3、溶质=溶液*浓度;4、溶液=溶质/浓度;(二)例题与解析1. 甲容器中有浓度为4%的盐水250克,乙容器中有某种浓度的盐水若干克。
现从乙中取出750 克盐水,放人甲容器中混合成浓度为8%的盐水。
问乙容器中的盐水浓度约是多少?A.9.78%B.10.14%C.9.33%D.11.27%答案:C解析:方法一:设乙容器中盐水的浓度为x(250×4%+750*x)/(250+750)=8%x=9.33%方法二:设浓度为x2. 甲、乙两瓶酒精溶液分别重300克和120克;甲中含酒精120克,乙中含酒精90克。
问从两瓶中应各取出多少克才能兑成浓度为50%的酒精溶液140克?A 甲100克,乙 40克B 甲90克,乙50克C 甲110克,乙30克D 甲70克,乙70克答案:A解析:甲浓度为40%,乙浓度为75%,甲中取A,乙中取140-AA:(140-A)=5:2A=1003、一杯含盐15%的盐水200克,要使盐水含盐20%,应加盐()克。
A.14.5B.10C.12.5D.15解析:假设加盐x克,15%的盐水200克, 100%的盐x克, 混合成20%的200+x.满足:15%*200+100%*x=20%*(200+x),所以可以用十字交叉法.解出x=12.5克.说明:浓度问题,无论是稀释、浓缩还是配制,一定要转化为甲、乙两种溶液混合成第三种丙溶液,方可利用十字交叉法。
浓度问题的十字交叉法原理浓度问题的十字交叉法原理在化学实验室里,我们经常需要处理各种化学反应液体的浓度问题。
比如,在配制溶液、制备试剂等情况下,我们需要准确地掌握物质的浓度,这就需要运用到浓度问题的计算。
而在浓度问题的计算中,十字交叉法是一种常用的方法。
那么,什么是十字交叉法,它的原理是什么呢?1. 十字交叉法定义十字交叉法是计算浓度问题的一种简便快捷的方法。
它是利用物质质量守恒定律和溶液质量守恒定律,通过常数项相等,求出未知浓度的方法。
其实就是利用溶液的比例关系,从而求出未知物质的质量或浓度。
2. 十字交叉法原理浓度问题的计算中,涉及到浓度、容积、物质质量等多个概念。
而十字交叉法主要是利用下面的两个公式:物质量守恒定律:m1 + m2 = m3其中,m1表示待求物质的质量,m2表示已知物质的质量,m3表示混合后物质的质量。
溶液质量守恒定律:c1V1 + c2V2 = c3V3其中,c1表示待求溶液的浓度,V1表示待求溶液的体积,c2表示已知溶液的浓度,V2表示已知溶液的体积,c3表示混合后溶液的浓度,V3表示混合后溶液的体积。
这两个公式,是十字交叉法成功的关键。
具体来说,十字交叉法通过交叉相乘消元,将未知量的系数解出来,进而得到待求物质的浓度或质量。
具体而言,十字交叉法包含以下四个步骤:(1)列出已知条件首先,我们需要清楚地了解题目中已知的条件是哪些。
这些条件可能包括物质的质量、溶液的浓度、溶液的体积等。
(2)列出方程根据上面的两个公式,我们可以列出一系列的方程,这些方程包括了已知条件,也包括未知物质的质量或浓度。
(3)十字相乘在十字交叉法中,我们需要进行十字相乘消元。
将等式两边的系数相乘,然后消去相同变量,最终求出待求物质的浓度或质量。
(4)检验答案最后,我们需要检验所求的答案是否正确。
这可以通过将所求的值代入原来的方程中,看看是否符合实际情况。
3. 十字交叉法的应用十字交叉法在化学实验室中有着广泛的应用。
奥数浓度问题十字交叉法
《奥数浓度问题十字交叉法》
一、定义
十字交叉法是指通过依次检测两点的解决问题的一种方法,将两点的测量结果用一条垂直直线连接起来,形成一个十字,从而得出浓度值的直观方法。
二、原理
十字交叉法用于测量奥数浓度的原理是:当两点的测量结果拟合一条垂直直线时,就可以用此条直线表示一种浓度的趋势,而此直线的直线斜率就是所测量到的浓度的值。
三、应用
十字交叉法可以用于测量奥数浓度,在测量时,测量者可以选择测量两点之间的任何一点,然后再用十字形线把两点连接起来,这样就可以得到更准确的浓度。
十字交叉法还可以用于测量其他不同类型的浓度,例如水中的悬浮物浓度、水中的碳水化合物浓度等。
四、优点
十字交叉法是一种比较常用的方法,它的优点在于:
1)简单实用,可以用于测量多种不同类型的浓度,能够得出非常准确的浓度值;
2)它可以将常量浓度的空间变化表示为一条曲线,使我们更容易理解这种浓度的变化趋势。
五、缺点
1)要在可能的最短时间内得出准确的浓度值,一定需要测量者对测试过程有足够的了解;
2)在测量复杂浓度时,由于浓度的变化趋势非常复杂,需要很多次的重复测量,以确保精确度。
浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口X贴着广告:“既甜又浓的豆浆每杯0.3元。
”黑熊便招呼弟弟们1,加歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,再加满水后,又给老二喝了一半,最后自己把剩下的一满水后给老三喝掉了3半喝完。
1=0.05(元);老三0.3狐狸开始收钱了,他要求黑熊最小的弟弟付出0.3×61=0.1(元);×31=0.15(元)。
兄弟一共付了0.45元。
老二与黑熊付的一样多,0.3×2兄弟们很惊讶,不是说,一杯豆浆0.3元,为什么多付0.45-0.3=0.15元?肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
”“不给,休想离开。
”现在,说说为什么会这样呢?专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量溶液质量×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。
浓度问题一个好玩的故事——熊喝豆浆黑熊领着三个弟弟在森林里游玩了半天,感到又渴又累,正好路过了狐狸开的豆浆店。
只见店门口张贴着广告:“既甜又浓的豆浆每杯0.3元。
”黑熊便招呼弟弟们歇脚,一起来喝豆浆。
黑熊从狐狸手中接过一杯豆浆,给最小的弟弟喝掉61,加满水后给老三喝掉了31,再加满水后,又给老二喝了一半,最后自己把剩下的一半喝完。
狐狸开始收钱了,他要求黑熊最小的弟弟付出0.3×61=0.05(元);老三0.3×31=0.1(元);老二与黑熊付的一样多,0.3×21=0.15(元)。
兄弟一共付了0.45元。
兄弟们很惊讶,不是说,一杯豆浆0.3元,为什么多付0.45-0.3=0.15元?肯定是黑熊再敲诈我们。
不服气的黑熊嚷起来:“多收我们坚决不干。
”“不给,休想离开。
”现在,说说为什么会这样呢?专题简析:溶质:在溶剂中的物质。
溶剂:溶解溶质的液体或气体。
溶液:包含溶质溶剂的混合物。
在小升初应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量溶液质量×100%=溶质质量溶质质量+溶剂质量×100%相关演化公式溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。
要根据题目的条件和问题逐一分析,也可以分步解答。
例题1有含糖量为7%的糖水600克,要使其含糖量加大到10%,需要再加入多少克糖?【思路导航】根据题意,在7%的糖水中加糖就改变了原来糖水的浓度,糖的质量增加了,糖水的质量也增加了,但水的质量并没有改变。
因此,可以先根据原来糖水中的浓度求出水的质量,再根据后来糖水中的浓度求出现在糖水的质量,用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。
解:原来糖水中水的质量:600×(1-7%)=558(克)现在糖水的质量:558÷(1-10%)=620(克)加入糖的质量:620-600=20(克)答:需要加入20克糖。
练习11、现在有浓度为20%的糖水300克,要把它变成浓度为40%的糖水,需要加糖多少克?2、有含盐15%的盐水20千克,要使盐水的浓度为20%,需加盐多少千克?3、有甲、乙两个瓶子,甲瓶里装了200毫升清水,乙瓶里装了200毫升纯酒精。
第一次把20毫升纯酒精由乙瓶倒入甲瓶,第二次把甲瓶中20毫升溶液倒回乙瓶,此时甲瓶里含纯酒精多,还是乙瓶里含水多?十字交叉法十字交叉法可用于溶液浓度的计算,例如溶液的稀释、浓缩或混合等计算题。
使用此法,使解题过程简便、快速、正确。
下面通过例题介绍十字交叉法的原理:同一物质的甲、乙两溶液的百分比浓度分别为a%、b%(a%>b%),现用这两种溶液配制百分比浓度为c%的溶液。
问取这两种溶液的质量比应是多少?同一物质的溶液,配制前后溶质的质量相等,利用这一原理可列式求解。
设甲、乙两溶液各取m1、m2克,两溶液混合后的溶液质量是(m1+m2)克。
列式m1×a%+m2×b%=(m1+m2)×c%,把此式整理得:m1:m2=(c-b)/(a-c),m1:m2就是所取甲、乙两溶液的质量比。
为了便于记忆和运算,若用C浓代替a,C稀代替b,C混代替C 如图把上式写成十字交叉法的一般形式,在运用十字交叉法进行计算时要注意,斜找差数,横看结果。
例题2 将20%的盐水与5%的盐水混合,配成15%的盐水600克,需要20%的盐水和5%的盐水各多少克?【思路导航】根据题意,将20%的盐水与5%的盐水混合配成15%的盐水,说明混合前两种盐水中盐的质量和与混合后盐水中盐的质量是相等的。
可根据这一数量间的相等关系列方程解答。
解:设20%的盐水需x 克,则5%的盐水为600-x 克,那么 20%x+(600-x )×5%=600×15% …… =…… X =400 600-400=200(克)答:需要20%的盐水400克,5%的盐水200克。
方法二解:用十字交叉法:配成15%的盐水600克,所需20%的盐水与5%的盐水比例为2:1,即 需要20%的盐水600×(2/3)=400克,需要5%的盐水600×(1/3)=200克,(或者600-400=200克) 答:需要20%的盐水400克,5%的盐水200克。
练习21、 两种钢分别含镍5%和40%,要得到140吨含镍30%的钢,需要含镍5%的钢和含镍40%的钢各多少吨?2、 甲、乙两种酒各含酒精75%和55%,要配制含酒精65%的酒3000克,应当从这两种酒中各取多少克?15%20%盐水5%盐水20%5%10%5%10% 5%=2:1例题3现有浓度为10%的盐水20千克。
再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水?【思路导航】这是一个溶液混合问题。
混合前、后溶液的浓度改变了,但总体上溶质及溶液的总质量没有改变。
所以,混合前两种溶液中溶质的和等于混合后溶液中的溶质的量。
解: 20千克10%的盐水中含盐的质量20×10%=2(千克)混合成22%时,20千克溶液中含盐的质量20×22%=404(千克)需加30%盐水溶液的质量(4.4-2)÷(30%-22%)=30(千克)答:需加入30千克浓度为30%的盐水,可以得到浓度为22%的盐水。
方法二解:用十字交叉法:练习31、在100千克浓度为50%的硫酸溶液中,再加入多少千克浓度为5%的硫酸溶液就可以配制成25%的硫酸溶液?2、浓度为70%的酒精溶液500克与浓度为50%的酒精溶液300克混合后所得到的酒精溶液的浓度是多少?3、在20%的盐水中加入10千克水,浓度为15%。
再加入多少千克盐,浓度为25%?例题4一种35%的新农药,如稀释到1.75%时,治虫最有效。
用多少千克浓度为35%的农药加多少千克水,才能配成1.75%的农药800千克?【思路导航】把浓度高的溶液经添加溶剂变为浓度低的溶液的过程称为稀释。
在这种稀释过程中,溶质的质量是不变的。
这是解这类问题的关键。
解: 800千克1.75%的农药含纯农药的质量为800×1.75%=14(千克)含14千克纯农药的35%的农药质量为14÷35%=40(千克)由40千克农药稀释为800千克农药应加水的质量为800-40=760(千克)答:用40千克的浓度为35%的农药中添加760千克水,才能配成浓度为1.75%的农药800千克。
方法二解:用十字交叉法:练习41、用含氨0.15%的氨水进行油菜追肥。
现有含氨16%的氨水30千克,配置时需加水多少千克?2、仓库运来含水量为90%的一种水果100千克。
一星期后再测,发现含水量降低到80%。
现在这批水果的质量是多少千克?3、一容器内装有10升纯酒精,倒出2.5升后,用水加满;再倒出5升,再用水加满。
这时容器内溶液的浓度是多少?例题5 甲、乙、丙3个试管中各盛有10克、20克、30克水。
把某种质量分数的盐水10克倒入甲管中,混合后取10克倒入乙管中,再混合后从乙管中取出10克倒入丙管中。
现在丙管中的盐水的质量分数为0.5%。
最早倒入甲管中的盐水质量分数是多少?混合后甲、乙、丙3个试管中应有的盐水分别是20克、30克、40克。
根据题意,可求出现在丙管中盐的质量。
又因为丙管中原来只有30克的水,它的盐是从10克盐水中的乙管里取出的。
由此可求出乙管里30克盐水中盐的质量。
而乙管里的盐又是从10克盐水中的甲管里取出的,由此可求出甲管里20克盐水中盐的质量。
而甲管里的盐是某种浓度的盐水中的盐,这样就可得到最初倒入甲管中盐水的质量分数。
丙管中盐的质量:(30+10)×0.5%=02(克)倒入乙管后,乙管中盐的质量:0.2×【(20+10)÷10】=0.6(克)倒入甲管,甲管中盐的质量:0.6×【(10+10)÷10】=1.2(克)1.2÷10=12%答:最早倒入甲管中的盐水质量分数是12%。
练习51、从装满100克80%的盐水中倒出40克盐水后,再用清水将杯加满,搅拌后再倒出40克盐水,然后再用清水将杯加满。
如此反复三次后,杯中盐水的浓度是多少?2、甲容器中又8%的盐水300克,乙容器中有12.5%的盐水120克。
往甲、乙两个容器分别倒入等量的水,使两个容器中盐水的浓度一样。
每个容器应倒入多少克水?3、甲种酒含纯酒精40%,乙种酒含纯酒精36%,丙种酒含纯酒精35%。
将三种酒混在一起得到含酒精38.5%的酒11千克。
已知乙种酒比丙种酒多3千克,那么甲种酒有多少千克?十字交叉法的其他应用数学统计某班一次数学测试,全班平均91分,其中男生平均88分,女生平均93分,则女生人数是男生人数的多少倍?( )A. 0.5B. 1C. 1.5D. 2生活问题一公斤鸡蛋有18个,一公斤鸭蛋有12个,一公斤鸡蛋和鸭蛋共有15个,则一公斤鸡蛋和鸭蛋中鸡蛋对鸭蛋个数比多大?较复杂的利润问题例2、某商店花10000进了一批商品,按期望获得相当于进价25%的利润来定价。
结果只销售了商品总量的30%。
为尽快完成资金周转,商店决定打折销售,这样卖完全部商品后,亏本1000元。
问商店是按定价打几折销售的?A、九折B、七五折C、六折D、四八折解析:该题属于利润问题,根据条件,这批商品分两个部分出售:30%的商品按25%的利润来定价出售,70%的商品打折后出售,最后总亏本1000元,即总利润为-10%。
设打折后出售的70%的商品的利润率为x,可用十字交叉法表示如下:得方程:,解得x=-25%。
则:×10=6答案选C。
浓度问题的方法总结基本公式浓度=—————×100%=——————×100%相关演化公式_____的重量+____的重量=溶液的重量____的重量÷___的重量×100%=浓度____的重量×浓度=溶质的重量_____÷_____=溶液的重量十字交叉法的方法总结浓度之十字交叉质量之十字交叉__________________________________________作业题“稀释”问题:特点是加“溶剂”,解题关键是找到始终不变的量(溶质)。