关于李雅普诺夫稳定性研究的读书报告

第4章李雅普诺夫稳定性分析李雅普诺夫稳定性分析是数学分析中的一个重要概念，它用于判断非线性系统在其中一点附近的稳定性。

李雅普诺夫稳定性分析方法最初由俄国数学家李雅普诺夫提出，广泛应用于控制论、微分方程和动力系统等领域。

在进行李雅普诺夫稳定性分析时，首先需要确定非线性系统的平衡点。

平衡点是指系统在其中一时刻的状态不再发生变化，即各个状态变量的导数为零。

在平衡点附近，可以通过线性化的方法来近似非线性系统，即将非线性系统转化为线性系统进行分析。

接下来，利用李雅普诺夫稳定性定理可以判断线性化系统的稳定性。

根据定理的不同形式，可以分为不动点稳定性定理和周期解稳定性定理。

不动点稳定性定理是指当线性化系统的特征根都具有负的实部时，非线性系统在平衡点附近是稳定的；而当至少存在一个特征根具有正的实部时，非线性系统在平衡点附近是不稳定的。

这个定理对于线性化系统为一阶系统或者线性化系统的特征根为复数的情况适用。

周期解稳定性定理是指当线性化系统的所有特征根满足一定条件时，非线性系统在周期解附近是稳定的。

这个定理对于封闭曲线解以及周期解的情况适用。

当线性化系统无法满足上述定理时，可以使用李雅普诺夫直接法来判断非线性系统的稳定性。

李雅普诺夫直接法是基于李雅普诺夫函数的概念，通过构造合适的李雅普诺夫函数来判断非线性系统的稳定性。

李雅普诺夫函数是满足以下条件的函数：1）李雅普诺夫函数的导数在其中一区域内是负定的，即导数的每个分量都小于或等于零；2）在平衡点附近，李雅普诺夫函数取得最小值。

通过构造合适的李雅普诺夫函数，并验证满足上述条件，就可以判断非线性系统的稳定性。

如果李雅普诺夫函数的导数在整个状态空间都是负定的，则非线性系统是全局稳定的；如果李雅普诺夫函数的导数在一些有限的状态空间内是负定的，则非线性系统是局部稳定的。

总之，李雅普诺夫稳定性分析是一种有力的工具，可以用于判断非线性系统的稳定性。

不过需要注意的是，李雅普诺夫稳定性分析方法仅适用于平衡点附近的稳定性分析，对于非线性系统的全局稳定性分析还需要其他的方法。

李雅普诺夫稳定性分析常微分⼤作业--李雅普诺夫稳定性11091059洪⼀洲从19世纪末以来，李雅普诺夫稳定性理论⼀直指导着关于稳定性的研究和应⽤。

不少学者遵循李雅普诺夫所开辟的研究路线对第⼆⽅法作了⼀些新的发展。

⼀⽅⾯，李雅普诺夫第⼆⽅法被推⼴到研究⼀般系统的稳定性。

例如，1957年，В．И．祖博夫将李雅普诺夫⽅法⽤于研究度量空间中不变集合的稳定性。

随后，J.P.拉萨尔等⼜对各种形式抽象系统的李雅普诺夫稳定性进⾏了研究。

在这些研究中，系统的描述不限于微分⽅程或差分⽅程，运动平衡状态已采⽤不变集合表⽰，李雅普诺夫函数是在更⼀般意义下定义的。

1967年，D.布肖对表征在集合与映射⽔平上的系统建⽴了李雅普诺夫第⼆⽅法。

这时，李雅普诺夫函数已不在实数域上取值，⽽是在有序定义的半格上取值。

另⼀⽅⾯，李雅普诺夫第⼆⽅法被⽤于研究⼤系统或多级系统的稳定性。

此时，李雅普诺夫函数被推⼴为向量形式，称为向量李雅普诺夫函数。

⽤这种⽅法可建⽴⼤系统稳定性的充分条件。

1.李雅普诺夫稳定性概念忽略输⼊后，⾮线性时变系统的状态⽅程如下),(t x f x= （1）式中，x 为n 维状态向量；t 为时间变量；),(t x f 为n 维函数，其展开式为 12(,,,,)i i n x f x x x t = n i ,,1 =假定⽅程的解为 ),;(00t x t x ，x 0和t 0 分别为初始状态向量和初始时刻，0000),;(x t x t x =。

平衡状态如果对于所有t ，满⾜0),(==t x f xe e （2）的状态x e 称为平衡状态（⼜称为平衡点）。

平衡状态的各分量不再随时间变化。

若已知状态⽅程，令0=x所求得的解x ，便是平衡状态。

对于线性定常系统Ax x= ，其平衡状态满⾜0=e Ax ，如果A ⾮奇异，系统只有惟⼀的零解，即存在⼀个位于状态空间原点的平衡状态。

⾄于⾮线性系统，0),(=t x f e 的解可能有多个，由系统状态⽅程决定。

基于正定二次型的李雅普诺夫稳定性分析摘要：李雅普诺夫稳定性理论以状态向量描述为基础，不仅适用于单变量、线性、定常系统，而且适用于多变量、非线性、时变系统。

但要应用李氏判据判断系统稳定性，就要涉及到系统矩阵A特征值的求解以及根据系统状态方程构造正定二次型的李雅普诺夫函数来判断系统稳定性。

1.问题的提出我们在处理实际工程问题时，经常需要判断系统稳定性，一般稳定性判据都有一定局限性，李雅普诺夫稳定性理论是确定系统稳定性的一般的理论，不仅适用于单变量、线性、定常系统，而且适用于多变量、非线性、时变系统，它以状态向量描述为基础，结合正定二次型的相关知识对系统稳定性进行判断。

2.问题的求解李雅普诺夫稳定性理论分析系统稳定性的两种方法：（1）利用线性系统微分方程的解来判断系统的稳定性——李雅普诺夫第一法（间接法）李雅普诺夫第一法的主要内容1）用一次近似式表示状态方程，即：X=AX+B(x)如果A的全部特征值都具有负实部，则系统在平衡点xe=0处是稳定的，且系统的稳定性与高阶项B(x)无关。

2）如果X=AX+B(x)的A的特征值中至少有一个具有正实部，则无论B(x)如何，系统在平衡点xe=0处为不稳定的。

3）如果X=AX+B(x)的A的含有等于零的特征值，则系统的稳定性由B(x)决定。

李雅普诺夫第一法是根据系统矩阵A的特征值来判断系统的稳定性的。

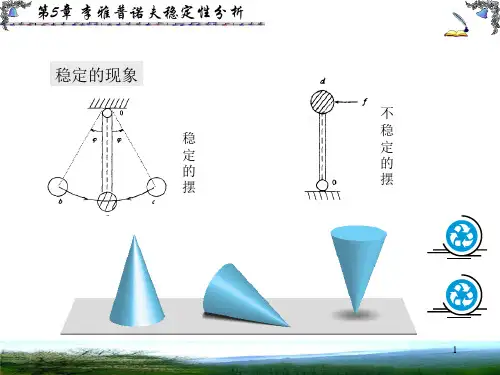
（2）构造李雅普诺夫函数，利用构造的李氏函数判断系统稳定性——李雅普诺夫第二法（直接法）观察振动现象，若系统能量(含动能和位能)随时间推移而衰减，则系统迟早会达到平衡状态。

基本思想：若系统内部能量随时间↑而↓,最终到达静止状态，系统稳定。

虚构一个能量函数（李雅普诺夫函数)V(x，t)=f（x1，x2，……x n，t）V(x)=f（x1，x2，……x n）V(x,t)或V(x)是一个标量函数。

能量总大于零，故为正定函数。

能量随随时间增加而衰减，即：V(x，t)或V(x)的导数小于零。

关于李雅普诺夫稳定性研究的读书报告摘要：本文通过对李雅普诺夫稳定性研究的深入阅读，总结了李雅普诺夫稳定性定理的核心内容和应用领域，并对其研究方法和意义进行了探讨。

通过深入理解和运用李雅普诺夫稳定性定理，可以有效地评估和预测非线性动力学系统的稳定性，对现实世界中的复杂系统具有重要的指导意义。

引言：李雅普诺夫稳定性是非线性动力学中的一个重要概念，对于理解和描述动力学系统的稳定性特性起到了至关重要的作用。

李雅普诺夫稳定性的理论研究成果为广大科学家提供了一种分析非线性系统稳定性的有力工具。

本文通过对相关文献的搜集和学习，对李雅普诺夫稳定性研究的核心内容、应用领域以及研究方法进行了总结和探讨。

一、李雅普诺夫稳定性定理的核心内容李雅普诺夫稳定性定理的核心思想是通过判断动力学系统的初始条件附近初始状态的微小扰动是否会被系统本身抵消，从而来判断系统的稳定性。

具体而言，李雅普诺夫稳定性定理包括三个重要定理：零稳定定理、相对稳定定理和绝对稳定定理。

零稳定定理指出，如果在某一初始状态下，系统的鲁棒性能指标能够保持在一个有限范围内，则该状态为零稳定状态。

相对稳定定理进一步强调了系统的稳定性特性，其指出，对于任意两个初始状态，如果它们之间的差异在某个范围内，则这两个状态之间的稳定性是相对稳定的。

绝对稳定定理则是对系统稳定性进行了更为严格的定义，它指出，如果在系统的任何一个初始状态下，初始状态的微小扰动都会随着时间的推移趋于零，则该系统为绝对稳定状态。

二、李雅普诺夫稳定性定理的应用领域李雅普诺夫稳定性定理广泛应用于各个领域的非线性动力学系统的研究中，包括力学、生物学、化学、电子工程等等。

在力学领域，李雅普诺夫稳定性定理可用于研究复杂机械系统的稳定性，例如弹性材料的动力学行为、混沌吸引子的存在与性质等。