1.3 高斯定理
- 格式:ppt
- 大小:2.17 MB
- 文档页数:38

高斯定理公式
高斯定理数学公式是:∮F·dS=∫(▽·F)dV。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定理(Gauss' law)也称为高斯通量理论(Gauss' flux theorem),或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况的高斯定理都是指该定理,也有其它同名定理)。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
扩展资料:
高斯定理指出:穿过一封闭曲面的电通量与封闭曲面所包围的电荷量成正比。
换一种说法:电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。
它表示,电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和,与曲面内电荷的位置分布情况无关,与封闭曲面外的电荷亦无关。
在真空的情况下,Σq是包围在封闭曲面内的自由电荷的代数和。
当存在介质时,Σq应理解为包围在封闭曲面内的自由电荷和极化电荷的总和。






高斯是德国数学家, 高斯是德国数学家, 也是科学家, 也是科学家,他和牛顿、 他和牛顿、 阿基米德, 阿基米德,被誉为有史 以来的三大数学家。
以来的三大数学家。
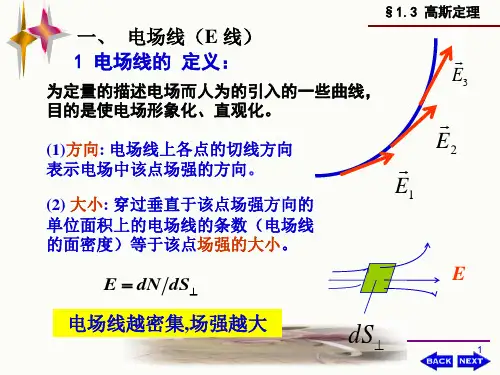
高 斯是近代数学奠基者之 一,在历史上影响之大, 在历史上影响之大, 可以和阿基米德、 可以和阿基米德、牛顿、 牛顿、 欧拉并列, 欧拉并列,有“数学王 子”之称 (C. F. Gauss , 1777—1855)1§1-3 高斯定理一、电场线 (electric line of field)+q1. 定义 -q 在电场中描绘一系列的曲线, 在电场中描绘一系列的曲线,使曲线上每一点的 切线方向都与该点处场强的方向一致; 切线方向都与该点处场强的方向一致; 在垂直于电场线的单位面积上穿过的曲线条数与 该处的电场强度的大小成正比。
该处的电场强度的大小成正比。
v ∆ Φ dΦ E = E ∝ lim = ∆S → 0 ∆ S dS 电场线的疏密程度表示场强大小的分布 电场线的疏密程度表示场强大小的分布, 表示场强大小的分布,其上任 一点的切线方向就是该点处的场强方向。
一点的切线方向就是该点处的场强方向。
不同电荷分布的电场线: 不同电荷分布的电场线:22. 性质 • 起于正电荷(或无限远),止于负电荷(或无限远); • 不闭合, 不闭合,也不在没有电荷的地方中断; 也不在没有电荷的地方中断; • 两条电场线在没有电荷的地方不会相交。
两条电场线在没有电荷的地方不会相交。
3二、电通量 (Electric Flux) 1. 定义 通过任一面积元的电场线的条数 通过任一面积元的电场线的条数称为通过这 电场线的条数称为通过这 一面积元的电场强度通量 一面积元的电场强度通量( 电场强度通量(简称电通量) 简称电通量) 。
v 如果垂直于电场强度的面积为 dS, 穿过的电 场线条数为dΦe,那么r S dsEv dΦe E∝ v dSv v (1) 如果在电场强度为 的匀强电场中,平面 S E 的匀强电场中, v 与电场强度 E 相垂直, 相垂直,则 Φe = E S 4若选择比例系数为1,则有dΦe = EdSv v v (2)如在场强为 E ,平面 S与场强 E 不 的匀强电场中 v 的匀强电场中, v 垂直, 垂直,其法线 n 与场强 E 成θ 角,则θ θΦ e = ES cosθ v v 或 Φe = E ⋅ SS cos θ(3) 非均匀电场强度电通量v v dΦ e = E ⋅ dS通过任一曲面S 的电通量: 电通量: v v Φe = ∫∫dΦe =∫∫ E ⋅ dSS S5思考题: 思考题:电场线与电通量的区别 (4) 任意闭合曲面的电通量 任意闭合曲面的电通量: 闭合曲面的电通量:v v Φ e = ∫∫ d Φ e = ∫∫ E ⋅ d SS S一个闭合曲面把整个空间分割成两部分: 一个闭合曲面把整个空间分割成两部分: 内部空间和外部空间 外法线矢量: 外法线矢量:指向曲面外部空间的法线矢量 内法线矢量: 内法线矢量:指向曲面内部空间的法线矢量62. 方向的规定: 方向的规定 闭合曲面的外法线方向为正。


高斯定理的解释和公式
高斯定理,也称为散度定理,是数学中的一个重要定理。
它描述了一个向量场通过一个封闭曲面的总量。
高斯定理在物理学和工程学的许多领域中都有广泛的应用,如电磁学、流体力学和热传导等。
高斯定理的数学表达形式如下:
对于一个平滑的三维矢量场F=(Fx,Fy,Fz),定义一个封闭曲面S来围绕一个具有体积V的区域D。
那么,高斯定理可以写作:
∬S F·dS = ∭D ∇·F dV
其中,F·dS表示向量场F在曲面元dS上的点积积分,∇·F表示向量场F的散度,dV表示体积元。
这个定理的物理解释是,对于一个流经封闭曲面的流体量,其发散性(流出和流入区域的总和)等于其在包围该区域的体积中的源和汇的总量。
高斯定理的应用非常广泛。
在电磁学中,它可以用来计算通过一个闭合曲面的电场强度和磁场强度的总量。
在流体力学中,它可以用来计算液体或气体通过一个封闭曲面的流量。
在热传导中,它可以用来计算热量通过一个封闭曲面的扩散量。
总之,高斯定理提供了一个非常强大的工具,用于计算向量场通过封闭曲面的总量。
它在物理和工程学中的应用使得我们能够更好地理解和分析各种自然现象和工程问题。

一)电通量引:§1--3高斯定理(Gauss Theorem)dΦ n E = 先回顾一下电力线密度的概念: ds n二)高斯定理dsn1表述:穿出任一闭合曲面的电通量 Φ e 等于该曲面内所包围的所有电荷的代数和除 以 ε 0 ,而与闭合面外的电荷无关。
Φ e = ∫ E ⋅ dS =S序程用应序程用应dΦ n1ε 0 S面内∑qi四)利用高斯定理计算具有对称性的电场通常是具有某种对称性 的电场--轴对称、球对 称、均匀场等。
序程用应例1)求半径为R均匀带电q的球壳所产生电场 的分布。
已知:R、q 求: (r ) E 解:1)分析对称性++ + + + + ++ + + + + O ++ ++ ++++ ++ + + + dq '++ ++ + + +++ ++ + + + ++++ + + ++E (r )qqRdq + +将电荷看成许多成对的点电荷 的集合r结论: 是以O为中心的 球对称电场。
+ + + ++++ + + + ++ + ++ + + + + ++ ++ + + + + ++ + + ++ + + 其球内也一样。
序程用应2)作半径为 r 的高斯球面E (r )S + + q q ++ + +(R ≤ r < ∞)E ⋅ dS = ∫S依高斯定理:+2∫ E cos 0 dS = ε ∑ qq2E 4π r =E (r) =1qε0E ∫ dS =S1ε0q4 πε 0 rˆ r或E (r) =4 πε 0 r内S0 S内3+ + +r+1ε0 1∑qSiiq rE (r )+ q++r+ + +3)作半径为 r 的高斯球面(0 ≤ r < R )1S∫ E cosθSdS = 0 ∴E = 0⎧0 ( 0 ≤ r < R ) ⎪ E=⎨ q ˆ r ( R ≤ r < ∞) ⎪ 4πε r 2 ⎩ 0E (r )R内S + +∫ E ⋅ dS = ε ∑ q0 Sir例2)一半径为R、均匀带电q的球体,求其电场 的分布。