当前位置：文档之家 › 7-3 静电场的高斯定理

7-3 静电场的高斯定理

  • 格式：ppt
  • 大小：2.00 MB
  • 文档页数：32

下载文档原格式

  / 32

合集下载

第4章-2-高斯定理

第4章-2-高斯定理

第二节 静电场的高斯定理 7-3
第四章 第七章
§4.2
静电场的高斯定理 基本内容： 基本内容：
一、电场线 二、电场强度通量 三、高斯定理
第二节 静电场的高斯定理 7-3 一. 规定 电场线
第四章 第七章
1） 曲线上每一点切线方向为该点电场方向, 曲线上每一点切线方向为该点电场方向, 切线方向为该点电场方向 通过垂直于电场方向单位面积 垂直于电场方向单位面积电场线的条 2） 通过垂直于电场方向单位面积电场线的条 数为该点电场强度的大小. 数为该点电场强度的大小.
第四章 第七章
一对不等量异号点电荷的电场线
2q
q
第二节 静电场的高斯定理 7-3
第四章 第七章
带电平行板电容器的电场线 + + + + + + + + + + + +
第二节 静电场的高斯定理 7-3
第四章 第七章
电场线的特点
始于正电荷,止于负电荷(或来自无穷远, 1） 始于正电荷,止于负电荷(或来自无穷远,去 向无穷远) 不会在没有电荷处中断. 向无穷远)，不会在没有电荷处中断. 电场线不相交. 2） 电场线不相交. 静电场电场线不闭合. 3） 静电场电场线不闭合. 电场线不仅能够表示电场强度的方向， 4) 电场线不仅能够表示电场强度的方向，而且 电场线在空间的密度分布还能表示电场强度的大小。 电场线在空间的密度分布还能表示电场强度的大小。
dS＇dS
+
任取两个球面， 任取两个球面，一 个包围曲面， 个包围曲面，另一 个在曲面内： 个在曲面内：则两 个球面的电通量都 q/ε 为q/ε0
通过任意形状的包围点电 的闭合面的电通量等于q/ q/ε 荷q的闭合面的电通量等于q/ε0
静电场的高斯定理

静电场的高斯定理

向平面）。
例7-10 求电荷呈“无限长”圆柱形轴对称均匀分布时 所激发的电场强度。
解：电场分布也应有柱对称性，方向沿径向。 作与带电圆柱同轴的圆柱形高斯面,
高为h,半径为r
•当r>R 时，
sE dS 侧面 E dS E 2 r h 为什么?
r h
E 2 r h h 0
P点的场强
E 2 0 r
1
0
d V
V
关于高斯定理的几点讨论
以上是通过用闭合曲面的电通量概念来说明高斯 定理，仅是为了便于理解而用的一种形象解释， 不是高斯定理的证明
高斯定理是在库仑定律基础上得到的，但是前者 适用范围比后者更广泛。后者只适用于真空中的 静电场，而前者适用于静电场和随时间变化的场， 高斯定理是电磁理论的基本方程之一。
③ 场源电荷为无限长均匀带电直线、均匀带电直圆柱面、直 圆柱体或同轴导体圆筒等，则电场的分布具有柱对称性。
(2) 选取高斯面
用高斯定理求场强时，选取恰当的高斯面是解题的关键。
选取高斯面的原则：
① 选取的高斯面必须通过所考查的场点。 ② 应使高斯面上各点的场强大小相等， 方向与该处面元 的
法线平行(这样则可将Ｅ提到积分号外，只对面积积分)； 或者使高斯的部分面上各点场强大小相等，方向与 的法线 平行，另一部分面上各点场强为零或场强的方向与面元的 法线垂直(即通过这部分的Ｅ通量为零)。
高斯定理解题步骤： 总结
(1)分析电场的对称性
根据题意画出示意图，分析电场的分布情况 (最好画出电场 线)，看是否具有某种特殊的对称性，这可从产生电场的场 源电荷的分布看出。
常见的情况有以下几种：
① 场源电荷为均匀带电球面、均匀带电球体、同心的均匀带 电导体球壳等，则电场的分布具有球对称性；
电场中的高斯定理

电场中的高斯定理

电场中的高斯定理高斯定律（gauss' law），属物理定律。

在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。

该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。

静电场中通过任意闭合曲面（称高斯面）s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率，与面外的电荷无关。

物理定律由于磁力线总是闭合曲线，因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来，否则这条磁力线就不会闭合起来了。

如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。

这个规律类似于电场中的高斯定理，因此也称为高斯定理。

与静电场中的高斯定理相比较，两者有著本质上的区别。

在静电场中，由于自然界中存有着单一制的电荷，所以电场线存有起点和终点，只要闭合面内有净余的也已（或负）电荷，沿着闭合面的电通量就不等于零，即为静电场就是有源场；而在磁场中，由于自然界中没单独的磁极存有，n极和s极就是无法拆分的，磁感线都就是无头无尾的滑动线，所以通过任何闭合面的磁通量必等于零。

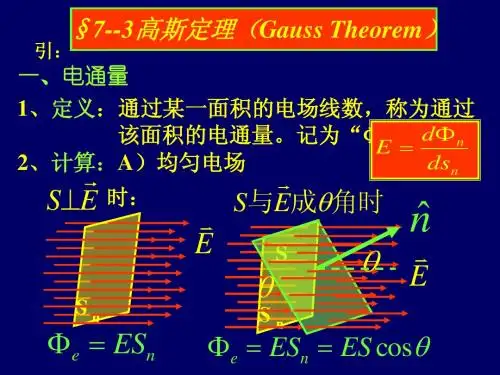
特别要强调两点： 1.关于电场线的方向的规定：电场线上每一点的切线方向就是该点电场的方向。

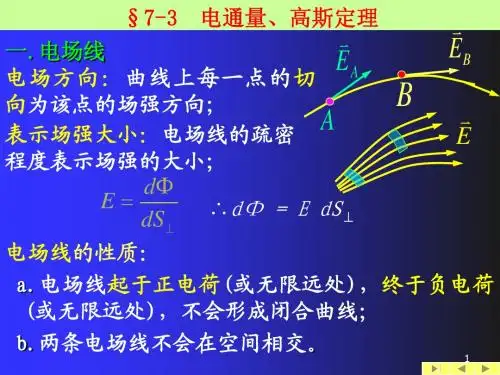
2.关于电场线的疏密的规定：电场线在某处的疏密要反映电场强度的大小，即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关，即： e=dn/ds，其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面，dn就是穿过该面ds的电场线的根数。

高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。

高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。

但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。

大学物理 第七章 高斯定理

大学物理 第七章 高斯定理

的电场。圆柱半径为R，沿轴线方向单位长度带电量为
。 解：电荷及场分布：柱对称性，场方向沿径向。
高斯面：与带电圆柱同轴的圆柱形
R
闭 合面,高为l,半径为r
sE dS 侧面 E dS E 2 rl
qin
0
由高斯定理知 E qin
2 0lr
r
l
上页 下页 返回 退出
（1）当r<R 时，高斯面内电荷量为：
半径R,电荷量为q
高斯面
E
问题关键：高斯面的选取
+ +P+
+
+q
+
A:球壳内任意一点P的场强如何求？
+ +
+ +
e E dS
0
+
+
+++ +
S
径向
上页 下页 返回 退出
e EdS EdS
S
s
E dS E 4 r2 0 S
E 0 (r R)
高斯面
E
+ +P+
+
+q
+
+
+
+ +
qin
q
4 R3
4r3
3
q
r
3
R
3
e EdS EdS E dS
S
S
S
E 4 r2 qin
0
E
高斯面
P+
+ +r +
+
E
qr
4 0 R 3
(r R)
上页 下页 返回 退出
静电学-高斯定理

静电学-高斯定理

S S i 1 i 1 S i 1
高斯定理:
1 E dS
S
0
q
S内
连续分布电荷:

1
0
Q e (r )dV
V
0
几点说明
• 高斯面上的电场强度与哪些电荷有关? • 通过高斯面的电通量与哪些电荷相关? 1, 高斯面上的电场与所有电荷相关 2, 高斯面是一个选择的闭合面 3, 穿入为负, 穿出为正 4, 仅高斯面内的电荷才会对高斯面的电通 量有贡献.
• 静电力是有心力，但高斯定理只给出了源和通 量的关系，并没有反映静电场是有心力场这一 特性，它只反映静电场性质的一个侧面（下一 节还要讲另一个定理——环路定理）
– 一般不能直接说高斯定理与库仑定律完全等价 – 若不添加附加条件（如场的对称性等），无法从高 斯定理导出库仑定理 – 电力平方反比律 ——Gauss定理 – 电荷间的作用力是有心力 ——Stokes定理
例子: 均匀带电球壳(半径R), 总带电 量为Q
• 计算空间各处的场强 (r>R, r<R) • 画出函数
举例， 均匀带电的无限大的面1个

E 2 0
举例， 均匀带电的无限大的面2个


高斯定理:
E dS
S V
Q EdV , Q
电荷相互作用是通过电场间的积压产生的.
• 现在人们知道电场也具有能量，而且和带电体相互作用， 交换能量；电场的能量可以转换成其它形式的能量如物体 的机械能、电池的化学能等。
电场的通量
电通量:
d E cos( )dS E dS
E dS
S
若S 为闭合曲面
大学物理chapter-7

大学物理chapter-7

F
q + F p 。 。 -q
E
0, M 0
稳定平衡
π, M 0
非稳定平衡
返回
退出
-
F
F
+
π 0 2 p -
-q 。 。 +q F
F
E
π π 2
+ F
E
p
F
E
在非均匀外电场中 电偶极子所受合力不为零， 力矩不为零。
返回
退出
sin 2 sin 1 Ex 4π 0 a
讨论
cos1 cos 2 Ey 4π 0 a
1. 无限长带电直线： 1 =0 ，2 =
P
Ex 0
E Ey 2 π 0 a
4 π 0 a
返回
退出
2、半无限长带电直线： 1 = 0 ，2 = /2 Ex E y
r a / sin
x a cot
dx a csc 2 d
cos 2 Ex a csc d 2 2 4π 0 a csc
2 1
Ex (sin 2 sin 1 ) 4π 0 a
(cos1 cos 2 ) 同理 E y 4π 0 a
第七章 静止电荷的电场
§7-1 物质的电结构 库仑定律 §7-2 静电场 电场强度
§7-3 静电场的高斯定理
§7-4 静电场的环路定理 电势 §7-5 电场强度与电势梯度的关系 §7-6 静电场中的导体 §7-7 电容器的电容 §7-8 静电场中的电介质 §7-9 有电介质时的高斯定理 电位移 §7-10 静电场的能量
11
静电场中的高斯定理

静电场中的高斯定理

静电场中的高斯定理：高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。

可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。

表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ （1）高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。

典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。

根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。

选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。

最后由高斯定理求出场强。

高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。

但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。

下面举一些例子来说静电场中高定理的应用：例1：一半径为R 的带电球体，其电荷体密度分布为()Ar r R ρ=≤，0()r R ρ=>，A 为大于零的常量。

7-3、高斯定理

7-3、高斯定理


E(r)
R
r
求无限大带电平面的电场。 例3：求无限大带电平面的电场。设电荷面密度为 σ。 v 对称性分析； 已知： 已知：σ， 求：E 解：对称性分析； + σ + ++ + + + + + ++ + + + 结论：以面为对称的场。 结论：以面为对称的场。与带电面等距离的 两平行平面处场强值相等。 两平行平面处场强值相等。
q + dq v + E(r) + r R q
+ + + + + ++ + + + + O ++ ++ ++++ ++ + + + ++ ++ + + +++ ++ + + + + + + ++++ + ++++ + + + ++ ++
将电荷看成许多成对的点电荷 的集合
dq'
结论： 结论： O为中心的球 以 对称电场。 对称电场。 + + + ++++ + + + ++ + ++ + + + + ++ ++ + + + + ++ + + ++ + + 其球内也一样。 其球内也一样。
大学物理(上)6静电场 下

大学物理(上)6静电场 下


v EA
v EB
B
1
二.电通量 电通量：通过电场中任一给定面的电场线条数； 电通量：通过电场中任一给定面的电场线条数； 条数 1.均匀电场中： 1.均匀电场中： 均匀电场中 a.平面S与场强垂直 则
S
ΦE = E⋅ S
S
θ
S⊥
2
v v 则 ΦE = E⋅ S⊥ = ES cos θ = E⋅ S 注： Φ 可正，可负，也可为零； E 可正，可负，也可为零；
电通量、 §7-3 电通量、高斯定理
一.电场线 电场方向： 曲线上每一点的切 电场方向 ： 曲线上每一点的 切 为该点的场强方向； 向为该点的场强方向； v A 表示场强大小： 表示场强大小：电场线的疏密 E 程度表示场强的大小； 程度表示场强的大小； dΦ E= ∴dΦ = E dS⊥ dS⊥ 电场线的性质 的性质： 电场线的性质： 电场线起于正电荷 或无限远处) 起于正电荷( a.电场线起于正电荷(或无限远处)，终于负电荷 或无限远处) 不会形成闭合曲线； (或无限远处)，不会形成闭合曲线； 两条电场线不会在空间相交。 b.两条电场线不会在空间相交。
Q
R
rP r r
o
E
r dS
S
r r E⋅dS = ∫ EdS ∫
S
= E∫dS = E4πr
S
S
2
10
求过场点的高斯面内电量代数和
r <R
r >R
∑q
∑q
i
i内
i内
=0
Q
i
R
rP r
i内
=Q
o
S
根据高斯定理列方程 解方程
E4πr =
2
∑q
高斯定理的理解

高斯定理的理解

高斯定理的理解电子与信息学院 0 7 电联 6号 熊德辉 摘要：高斯定理在静电学具有重要的应用。

在大学物理里，仅表示为积分形式，应认识其物理意义 ,同时又必须从它的物理含义上认识它的数学应用 ,这对清楚、全面了解静电场是至关重要的.关键词:高斯定理;高斯面;电场线;对称分布;散度；电通量;电场强度。

一、高斯定理的理解高斯定理是静电学中的一个重要定理,它反映了静电场的一个基本性质 ,即静电场是有源场 ,其源即是电荷。

可表述为:在静电场中 ,通过任意闭合曲面的电通量 ,等于该闭合曲面所包围的电荷的代数和的ξ1倍 ,与闭合曲面外的电荷无关。

它的表达式为：ξint∑⎰=∙qdS E s是电磁学最基本的定理之一。

其中 ,E 表示在闭合曲面上任一 dS 面处的电场强度 ,而 E ·dS 则为通过面元dS 的电场强度通量 ,就表dS E s∙⎰示通过整个闭合曲面 S 的电场强度通量 ,⎰s表示沿闭合曲面 S 的积分 ,习惯上称 S 为高斯面， 高斯定理表明:静电场是有源的、发散的 ,源头在电荷所在处 ,由此确定的电场线起于正电荷 ,终于负电荷。

对高斯定理的理解和应用不正确 ,常常会出现一些问题。

如 ,高斯面上的 E 是否完全由高斯面内的电荷产生;如果 ∑=0q ，是否必有 E = 0 ;当E 处处为零时 ,是否高斯面内一定无电荷;高斯定理是否在任何情况下都成立;哪些问题用高斯定理解决会简便一些等等. 这就涉及是否对高斯定理理解正确 ,对其数学表达式的理解是否存在数学负迁移情况.其实 ,只要对高斯定理注意掌握几个要点， 就能对上面的问题有比较清醒的认识了.1 定理中的 E 是指空间某处的总电场强度空间中某处的电场强度为空间中所有电荷所激发的电场在该处场强的矢量和. 若任意作一个假想的闭合曲面(高斯面) 通过该处 ,用 E 内、 E 外 分别表示高斯面内、外的电荷在高斯面上产生的场 ,则在该处的总场强 E = E 内 + E 外.由高斯定理有:ξint∑⎰⎰⎰=∙+∙=∙qdS dS dS E sssE E外内而从电场线的角度看 ,电场线始于正电荷 ,终于负电荷 ,当电场中的闭合曲面内不含有电荷时 ,电场线仅穿过此闭合曲面 ,这些进入闭合曲面的电场线总条数与穿出闭合曲面的电场线总条数相等 ,故通过整个闭合曲面的电场强度通量为零. 所以 0=∙⎰dS sE 外故 ξint∑⎰⎰=∙=∙qdS dS E ssE 内即:高斯定理对高斯面内的电荷产生的场而言 ,也成立.2 注意ξ0int ∑⎰=∙qdS E s中 E 和 dS 的矢量性在对高斯定理的理解上常常出现不注意物理量的矢量性问题. 有些人认为当0int=∑q 时 ,由于dS ≠0 ,所以必有 E = 0.实际上 , 0int=∑q ,表明始于闭合曲面内正电荷的电场线与终于闭合曲面内负电荷的电场线数相等 ,则穿出闭合曲面的电场线数与进入闭合曲面的电场线数相等 ,即通过整个闭合面的电场强度通量为零.但这并不意味着闭合曲面上电场强度处处为零. 因为:(1) 高斯面上某处的场强是高斯面内、外电荷在该处产生的场强的矢量和 ,所以 ,即便高斯面内的0int=∑q ,也无法完全确定 E =0 ;(2) 由于 E 和dS 在式中是矢量的标积关系 ,因此存在二者的方向问题 ,如果 E ≠0 ,而它与dS 的方向垂直 ,仍有 E ·dS = 0. 故不能由 0int=∑q 来判断 E 是否为零。

静电场的高斯定理

静电场的高斯定理


q
+S
r
与球面半径无关，即以点电荷q 为中心的任一
球面，不论半径大小如何，通过球面的电通量
都相等。
31
2）点电荷在任意闭合曲面 S ' 内
S '和 S 包围同一个点电荷。由于电场线的连
续性，通过两个闭合曲面的电场线的数目是相
等的，所以 e e
通过 S ' 的电通量：
E dS
3点电荷在闭合曲面之外若将前几例中等式右面的q理解为封闭面内的电荷此处的0可以和前面的结果统一起344在点电荷系的电场中通过任意闭合曲面的电通量面内电荷面外电荷35gausslaw在真空中的静电场内通过任一闭合曲面的电通量等于该闭合曲面所包围的电荷电量的代数和除以为高斯面上各点的电场强度是由所有内外电荷共同产生的总电场强度
求解的关键是选取适当的高斯面。
常见的具有对称性分布的源电荷有：
40
常见的对称性电荷分布类型：
球对称分布： 均匀带电的球面，球体和多层
同心球壳等
轴对称分布： 无限长均匀带电的直线，圆柱面，
圆柱壳等；
平面对称分布： 无限大的均匀带电平面，平板等。
17
电场线是按照下述规定在电场中画出的一 系列假想的曲线：
方向：曲线上每一点
的切线方向与该点的
E
场强方向一致；
大小：通过电场中某点，垂直于场强的单位面
积的电力线根数，等于该点电场强度的大小。
ds E dN
E
dS
电场线稀疏的地方场强小，
dS
电场线密集的地方场强大1。8
电场线的性质
①电场线起始于正电荷(或无穷远处)， 终止于负电荷，不会在没有电荷处中断；
其外表面上的通量为

静电场中的高斯定理

目录1前言 (1)2静电场中的高斯定理的定义 (1)3高斯定理的推导过程 (2)3.1电场线 (2)3.2电场强度通量 (3)3.3高斯定理的推导 (4)4高斯定理的应用 (6)参考文献： (8)静电场的高斯定理X慧君（学号：20111104295）（物理与电子信息学院11级电子信息工程1班，某呼和浩特010022）指导教师：X淑琴摘要：本文意在论述静电场中的高斯定理的定义、推导过程以及其在静电场中的应用方法。

方法是通过讨论电通量与场源电荷之间的关系得出高斯定理，应用高斯定理求解几种情况下的场强大小及其分布情况，然后根据例题总结出高斯定理在静电场中应用的方法。

关键词：静电场；高斯定理；定义；推导过程；应用方法中图分类号：O44 文献标识码：A1前言电磁学是研究电磁相互作用和电磁运动基本规律的一门学科，是经典物理学的一个重要分支，也是近代物理学不可缺少的基础。

而静电场中的高斯定理就是电磁学的一部分，同时静电场中的高斯定理是电磁学中的重要定理之一。

以前我们学习了匀场电场中有关场强的解答方法，但如果是在场强分布不均匀的电场中，我们又该怎样解出场强来呢？或许你想到了运用高等数学里所学习的积分来解答，积分对于大多数人来讲它过于复杂了。

还有没有更加简单快速的方法呢？学习了静电场中的高斯定理之后，你会发现：原来一切都是那么简单。

是的，运用静电场中的高斯定理你无需在使用复杂的积分，你只需要做一个简单的高斯面就可以快速解答一切有关求场强的问题了。

无论它有多么复杂，只要你熟练掌握了静电场中高斯定理的应用方法。

2静电场中的高斯定理的定义静电场中的高斯定理是电磁学中的重要定理之一，表述为：在静电场中，通过任意，而与闭合曲面外闭合曲面S的电通量等于该面所包围的所有电荷电量的代数和除以的电荷无关；数学公式表示为⎰⎰∑=SqS dEε式中⎰⎰s表示沿一个闭合曲面S的积分，该闭合曲面S通常称为高斯面。

由上式可以看出闭合曲面的电通量只与闭合面内的电荷有关，闭合面外的电荷对闭合曲面的电通量没有贡献。

高斯定理的证明方法和应用

S
（1）
其中 S 取外侧。(1)式称为高斯公式。 1、 物理上静电场的高斯定理
在一半径 r 的球面 S 包围一位于球心的点电荷 Q，在这个球面上，场强 E 的方向处 处垂直于球面，且 E 的大小相等，都是 E
Q 4 0 r 2
。通过这个球面 S 的电通量为
e E dS E dS 4 r 2 E





式中最后一步用到 函数的筛选性，将式（3）代入式（2）中得：
r SE dS V 0 dV
（1） 当电荷 Q 包含在闭合曲面 S 内时，则
7
r Q E d S d V S V 0 0
高斯定理的证明方法和应用
高斯定理是电磁学的一条重要定理，这里对高斯定理作了比较详细的介绍，并提 供了数学法、直接证明法等方法证明高斯定理，以及介绍高斯定理的应用和使用高斯定 理应注意的问题，从中可以发现高斯定理在解决电场和磁场学中的方便之处。 关键字：高斯定理、高斯公式、证明、方法、应用 高斯定理又叫散度定理，高斯定理在物理学研究方面，应用非常广泛，应用高斯定 理求曲面积分、静电场、非静电场或磁场非常方便，特别是求电场或者磁场中的场强。 虽然有时候应用高斯定理求电场或者磁场中的场强问题很方便，但是它也存在一些局限 性，所以要更好的运用高斯定理解决电场和磁场学问题，我们首先应对高斯定理有一定 的了解。
（2） 当电荷 Q 不包含在闭合曲面 S 内时，则
S V
r E dS dV 0
0
由此，高斯定理得证。 3、 高斯定理的另一种证明
如图所示，设有一电量为 q 孤立的正点电荷，现以点电荷所在处为球心，任意 r 为 半径作一球面为高斯面，球面上任意点的场强为

静电场的高斯定理

dS dS 显然有： 2 2 dΩ （立体角 ） r r q 故 E dS dS 2 40 r q q q E dS dS dS 2 2 40 r 40 r 0 S S
下午1时41分
r
dS
dS
r
解 对称性分析：轴对称
选取闭合的柱形高斯面
z
en
+ +

+
S
E dS
E dS
S ( 柱侧面）

E dS
E
l
S ( 上底）

S (下底）

E dS
S ( 柱面）

E dS
r
x
+ +
o y
e n en
+
E dS
当电场线穿入高斯面： dΦ E dS 0 e
E
S dS
下午1时41分
11
例1：在均匀电场中有一立方形的闭合面（如图）
E ( 240 N c )i
通过该闭合面的电通量是多少？
y
x
z
下午1时41分 12
【课堂练习1】 求均匀电场中一半球面的电通量。
S
l EdS 0 S ( 柱面）
l
z
+ +
l E 2πrl 0
E
E 2 π 0 r
r
x
+
+
+
o y
en
【例】无限大均匀带电平面的电场强度 无限大均匀带电平面，单位面积上的电荷，即电 荷面密度为 ，求距平面为 处的电场强度.

7.3 高斯定理


π θ 2
闭合面上各面元的外法线 方向为正向。 面内指向曲面外。
即各个面元的 n 总是从曲
E

π θ 2
π θ ， E dS 0 电力线穿出闭合面为正通量， 2 π θ ， E dS 0 电力线穿入闭合面为负通量。 2
e

S
EdS cos
E
n
1.高斯定理的表述
对真空中的静电场，通过任一闭合曲面(高斯 面)的电通量等于该闭合曲面所包围的电荷电 0 量的代数和除以
e

S
E dS
Q
i
i内
0
高斯定理可由库仑定律和场强叠加原理导出。
2.高斯定理的导出 1）点电荷位于球面 S 中心
E
Q 4 0 r
2
e

S
E dS
例
求均匀带电球体的电场。（已知 q、R）
E 具有球对称性.
解： 对称性分析
取球形高斯面. r < R 时
e
q 4 3 dV r 3 (4 R / 3) 3 VS内

S
E dS E 4 r 2
E
q
r
R
由高斯定理，
3 1 qr 2 E 4 r 3 0 R
球内场强：
r E 3 0 4 0 R 3
qr
(r < R)
r>R时
电通量 e 电量

S
E dS E 4 r
2
VS内
dV q
2
E
由高斯定理
r
q R
E 4 r q 0
场强
E
q 4 0 r

高二物理竞赛课件-7.3静电场的高斯定理

第七章 静止电荷的电场
§7-3 静电场的高斯定理
1
第七章 静止电荷的电场
7.1 物质的电结构 库仑定律
7.2 静电场 电场强度
7.3 静电场的高斯定理
7.4 静电场的环路定理 电势
7.5 电场强度与电势梯度的关系
7.6 静电场中的导体
7.7 电容器的电容
7.8 静电场中的电介质
7.9 有电介质时的高斯定理 电位移
高斯定理并未反映静电场是有心力这一特点。 实际上，不增加附加条件(如点电荷电场的方向沿径向或 具有球面对称性等条件)并不能从高斯定理推出库仑定律。
在静电场范围内，库仑定律比高斯定理包含更多的信息: 库仑定律将电场强度和电荷直接联系起来； 高斯定理将电场通量和某一区域内的电荷联系在一起。
17
高斯定理 讨论 (3)
因为高斯面外的电荷对在高斯面上产生的电通量没有贡献，但其对总场强有贡献。
q 其值等于dS2面内的电通量，
（2）通过包围点电荷q 的任意闭合面S的电通量都 =
4 r 高斯定理 讨论 (2)
2
直接运用高斯定理求出场强的情形，须有一定的对0 称性。
如
,则S 上各点E = 0 ?
解：柱面外一点对称性分析：任一点(P)的场强沿径向，距中心同远处场强相同。
电荷间的作用力有平方反比关系；
解：柱面内一点对称性分析：圆柱内任一点的场强沿径向。
电偶极子 如S上各点E=0，能否肯定此闭合面内一定没有包围净电荷?
(中线、延长线)
中垂线
2 0
1
x
x2
R2
1 E
r3
中垂线
2 0 r
19
例题 7-9
求均匀带正电球壳所激发的场强。(R, q)

静电场的高斯定理内容

静电场的高斯定理内容
静电场的高斯定理是物理学家高斯发现的一种物理定律，它解释了电场的特殊状态。

它表明，在任何场的定义空间中，对于任何闭合曲面的一边，电场的积分值等于以曲面的另一边为主的带电体上电荷量的积分值。

这个定理在推导电场的特性时具有重要的意义，也可用来计算某些情况下电场的强度，从而研究电场的变化规律。

具体而言，静电场的高斯定理可表示为：
∮E·dS=ρ/ε
其中，E表示电场强度，dS表示曲面的元素，ρ表示曲面另一边为主的带电体上电荷量，ε表示空气的介电常数。

静电场的高斯定理还可以写成另一种形式：·E=ρ/ε
其中，表示梯度操作，也就是在进行静电场的空间分析或变分计算的时候，要用到的梯度操作。

高斯定理可以说是电势学的基石，它包含了电场和电荷之间的重要关系，为研究电荷的运动提供了重要的参考。

它可以用来计算复杂情况下的电场强度，进而推导与其相关的电势能量的变化情况，从而研究电场的运动规律。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

q

q
z
0
底面
R O
q [1 2 0
z z R
2 2
]
§7-3 静电场的高斯定理
2、电场线密度与场强的关系
dS
EA B
A
dS dΦ
EB
垂直于考察点场强的面元 通过 dS 的电场线数目 dΦ E dS
§7-3 静电场的高斯定理
【电通量】通过电场中任一曲面的电力线数目 1、匀强电场中任一平面的电通量
n

S
E
S
S

E
(1) E // n
0
(r<R)
E
r R
Q 2 4o r
r R
E
E0
O
E
Q 40 r 2
r
R
§7-3 静电场的高斯定理
例2 求半径为R、电荷体密度为 的均匀带电球体的电场
r
r
3 R E |r R r 3 3 0 r
E |r R r 3 0
§7-3 静电场的高斯定理
E
R1
R1 R2
R2
r
俯视图
§7-3 静电场的高斯定理
[例5] 在半径为R1,电荷密度为 的均匀带电球体
内，挖去以半径R2的球形空腔。空腔中心C2与带电 球心C1间距为a，且R1 >a> R2。求空腔内任意点的 电场强度。
C2 R1
a
C1
R2

§7-3 静电场的高斯定理
【填补法】 1、先填满空腔
q
i内
r
r
S
λ
S
O R
l
S r E O P
轴对称
E
o

p
S
E
球对称 高斯面选取的规则：
面对称
1. 符合带电体电场分布的几何对称性； 2. 便于沿高斯面的积分：
e E dS
S
E ∥ dS E dS
e E dS
S
e 0
e E dS ES
q Φ ε0 Φ每 个 面 q 6ε0
q
§7-3 静电场的高斯定理
[例2] 若将电荷为q 的点电荷置于立方体的
一个顶角上，求每个面上的电通量。
e
h
d
g
f
c
b
qa
一个电量为q的点电荷位于立方体的顶点A上，则通 过侧面abcd的电通量等于多少？
a
d b
q
A
A q
c
1 1 q e 0 6 4 24 0
E 0
( r R)
E
E0
O
E 20 r
r
R
无限长均匀带电圆柱体。
E 2 0 r
(r R) (r R)
r E 2 0 R 2
E
E 20 r
0
R
r
例4 设有两个无限大均匀带电同轴圆柱面，半径分别 为R1和R2，带有等量异号的电荷，单位长度的电量分 别为。求场强分布。
EA EB
在以直线为轴的圆柱面上， 电场强度大小相同。
§7-3 静电场的高斯定理
例3 求电荷线密度为 的无限长均匀带电直线的电场。 n
l
n
R
Eபைடு நூலகம்
E
E 2 o r
无限长均匀带电圆柱面。
l E 2r l 0
E 2 0 r
(r R)
E 2r l 0
§7-3 静电场的高斯定理
一对等量同号点电荷
一对等量同号点电荷
平行板电容器
平行板电容器
§7-3 静电场的高斯定理
１、电场线的性质
q
-q
(1) 电场线起自正电荷(或无穷远)，止于负电荷 (或无穷远)，但不会在没有电荷的地方中断；
(2) 静电场中的电场线不形成单向闭合线； (3) 任意两条电场线在无电荷处不会相交。
1 E dS
S
0
q
in
E 2rl 0 E0
-
R2
r l + + + +
R1
+ + + +
R1
俯视图
R2
3) 在外圆柱面之外， r>R2
1 E dS
S
E 2rl 0 E0
0
q
in
-
R2
R1
r
- l -
+ + + +
+ + + +
S
且，尽量使E 与dS 无关
§7-3 静电场的高斯定理
例1 求半径为 R的球面均匀带电荷Q时的电场分布。
dE
A
EA
dE
分析电场分布特点 结论一： E 的方向一定沿着径向；
r + dS+
+ + + +
+ +
+
+
dS
结论二：
+ + +
+
+ + r
EA EB EB
q内
0
q
R
q
E
讨论：
1）点电荷不在球面中心； 2）若为任意封闭曲面呢？ 3）若点电荷在封闭曲面外呢？ 4）若封闭曲面内有多个点电荷呢？
§7-3 静电场的高斯定理
E dS
S
q
0
i内
说明： （1） s E dS 取决于 qi内 E 取决于空间所有电荷分布；
B
在以球心为圆心 的球面上，电场强 度大小相同。
§7-3 静电场的高斯定理
高斯面
+
+ + + + + + + +
+
+ +
+
+
+ + + + + + +
+
+ +
+ + + + +
r
r
+ + +
E |r R
Q r 3 4 0 r
E |r R 0
半径为R的球面均匀带电荷Q时的电场分布。
q
§7-3 静电场的高斯定理
[例3] 将电荷为q 的点电荷放置于半径为R的 圆盘的中轴线上， 距离圆盘中心为z， 求圆盘上的电通量。
q
z
O
R
q Φ [1 2ε0
z z R
2 2
]
§7-3 静电场的高斯定理
[例4] 将电荷为q的点电荷放 置于底面半径为R的锥体内， 并位于中轴线上，距离底面 为z，求侧面的电通量。
(2) E n θ
§7-3 静电场的高斯定理
2、电场中任一曲面的电通量
dS

E
§7-3 静电场的高斯定理
3、电场中任一闭合曲面的电通量
规定：闭合曲面的“外法向”为“正方向”
dS
dS θ
E2
1
E1
§7-3 静电场的高斯定理
例1 以点电荷为球心, 半径为R的球面的电通量。 结果：
解：电荷分布具有轴对称，作同轴的封闭圆柱面
l -
+ + + +
R1
R2
q内 由高斯定理： SE dS 0 E dS E dS E dS E dS E 2rl
上 下 侧 侧
为高斯面，底面半径为r，高度为l。
半径为R、均匀带电荷Q的均匀带电球体的电场分布
r
R
E
E
Qr 4o R 3 Q 2 4o r
r R
r R
0
R
r
§7-3 静电场的高斯定理
例3 求电荷线密度为 的无限长均匀带电直线的电场。
分析电场分布特点： 结论一：
P
E的方向一定沿着垂直于
直线的方向 EA
O
Q B
A
结论二：
E2 r2 3 0
R1
a
C1
C2
r1
R2
r2
E1
P
E2
E
E1 r1 3 0

2、电场叠加原理
E E1 E 2
E a 3 0
§7-3 静电场的高斯定理
[例1] 若将电荷为q的点电荷置于立方体的中央， 求每个面上的电通量。
§7-3 静电场的高斯定理
【电场线】形象描述电场的一簇虚拟有向曲线。
EA B
A
EB
规定：对电场线上任一点 切向 密疏
E 的方向 E 的大小 E A E B
§7-3 静电场的高斯定理
几种典型带电体的实验场线（左）与理论场线（右） 无 穷 远
点电荷
正、负点电荷
一对等量异号点电荷
一对等量异号点电荷
（2）意义 ——表明静电场是有源场。
（3）高斯定理源于库仑定律， 但又高于库仑定律。
q1 q2
q3
p
S
q4
qN
§7-3 静电场的高斯定理
解题步骤
①对称性分析，确定 E 的大小及方向分布特征
②作高斯面，计算电通量及 ③利用高斯定理求解 选取高斯面的技巧：