白噪声讲义

§3.7通信原理之白噪声
通信原理之白噪声综述
1.1 白噪声
定义：凡功率谱密度在整个频域内都是均匀分布的噪声，称为白噪声。

即：
双边谱密度：
单边谱密度：
其中：n0为常数，W/Hz。

一般默认白噪声为平稳的。

1.2 白噪声的功率
由于白噪声的带宽无限，其平均功率为无穷大。

即或。

因此，真正“白”的噪声是不存在的，它只是构造的一种理想化的噪声形式。

实际中，只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带，我们就可以把它视为白噪声。

如果白噪声取值的概率分布服从高斯分布，则称之为高斯白噪声。

高斯白噪声在任意两个不同时刻上的随机变量之间，不仅是互不相关的，而且还是统计独立的。

1.3 自相关函数
据：功率信号的功率谱密度与其自相关函数互为傅氏变换对。

图3-6 白噪声的功率谱密度与自相关函数
图3-6 白噪声的功率谱密度与自相关函数
2.1 带限白噪声
1.低通白噪声白噪声经理想低通滤波器| f |≤后而形成的噪声，被称为低通白噪声，即其功率谱密度为：
由上式可见，白噪声的功率谱密度被限制在| f |≤内，通常把这样的噪声也称为带限白噪声。

2.2带通白噪声
白噪声经理想带通滤波器后而形成的噪声，被称为低通白噪声，即其功率谱密度为：
式中：f c －中心频率，B－通带宽度则其输出噪声的功率谱密度为：
2.3窄带高斯白噪声
通常，带通滤波器的 B << fc ，因此称窄带滤波器，相应地把带通白高斯噪声称为窄带高斯白噪声。

其统计特性与一般窄带随机过程相同：
平均功率N=n0B。

白噪声的定义式白噪声是一个经典的信号处理问题，它在工程、物理、生物等领域都有广泛的应用。

在本文中，我们将介绍白噪声的定义式，并探讨其在实际应用中的意义和应用。

1. 白噪声的定义白噪声是一种特殊的随机信号，其功率谱密度在所有频率范围内均匀分布，即具有平坦的功率谱密度。

这意味着在所有频率上，白噪声的功率都是相等的。

白噪声的名称源于其类似于白光的性质，即白光是由所有频率的光波组成的，而白噪声是由所有频率的信号组成的。

白噪声的数学定义式为：$$P(f)=K$$其中，$P(f)$ 是白噪声在频率 $f$ 处的功率谱密度，$K$ 是一个常数。

这个定义式表示白噪声在所有频率上具有相同的功率，即功率谱密度是常数 $K$。

在实际应用中，我们通常使用功率谱密度的对数形式来描述白噪声的特性。

因为在对数坐标下，平坦的功率谱密度将呈现为一条水平的直线。

因此，我们可以将白噪声的定义式改写为：$$log P(f)=log K$$这个等式表示在对数坐标下，白噪声的功率谱密度是一个常数。

2. 白噪声的特性白噪声具有以下特性：(1) 平稳性：白噪声是一种平稳随机过程，即其统计特性在时间上不变。

这意味着在任何时间点，白噪声的统计特性都是相同的。

(2) 独立性：白噪声的各个样本之间是相互独立的。

这意味着在任何时间点，白噪声的各个样本之间是不相关的。

(3) 均匀性：白噪声的功率谱密度在所有频率上均匀分布。

这意味着在所有频率上，白噪声的功率都是相等的。

(4) 白噪声是高斯分布的：白噪声的各个样本是服从高斯分布的。

3. 白噪声的应用白噪声在实际应用中有广泛的应用。

以下是一些常见的应用领域：(1) 信号处理：白噪声在信号处理中有广泛的应用，例如在滤波、降噪、信号分析等方面。

(2) 通信系统：白噪声在通信系统中也有广泛的应用，例如在信道建模、信道估计、信号检测等方面。

(3) 物理学：白噪声在物理学中也有重要的应用，例如在热力学、量子力学、天文学等方面。

白噪声白噪声是指功率谱密度在整个频域内均匀分布的噪声。

所有频率具有相同能量密度的随机噪声称为白噪声。

从我们耳朵的频率响应听起来它是非常明亮的“咝”声（每高一个八度，频率就升高一倍。

因此高频率区的能量也显著增强）。

1概述白噪声是指在较宽的频率范围内，各等带宽的频带所含的噪声能量相等的噪声。

一般在物理上把它翻译成白噪声（white noise）。

白噪声或白杂讯，是一种功率频谱密度为常数的随机信号或随机过程。

换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。

相对的，其他不具有这一性质的噪声信号被称为有色噪声。

理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。

实际上，我们常常将有限带宽的平整讯号视为白噪音，因为这让我们在数学分析上更加方便。

然而，白噪声在数学处理上比较方便，因此它是系统分析的有力工具。

一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。

例如，热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度，通常可以认为它们是白噪声。

当你需要专心工作，而周遭总是有繁杂的声音时，就可以选用这两种声音来加以遮蔽。

一般来说，通常的情况下你可以选用白色噪音，而粉红色噪音则是特别针对说话声的遮蔽材料。

粉红色噪音又被称做频率反比(1/f) 噪音，因为它的能量分布与频率成反比，或者说是每一个八度音程(Octave) 能量就衰退3 dB。

高斯白噪声高斯白噪声：如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。

热噪声和散粒噪声是高斯白噪声。

所谓高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。

白噪声的科学原理在平静的夜晚，你是否曾经听到过窗外传来的嘈杂声？或者是邻居打扫卫生的吵闹声？这些声音会干扰你的休息，使你难以入眠。

对于这种情况，很多人会选择使用白噪声来解决问题。

那么白噪声到底是什么？它是如何产生的？本篇文章将介绍白噪声的科学原理。

一、什么是白噪声？白噪声是一种特殊的声音信号，它是由一系列的等能量频率组成。

相比其他类型的信号，白噪声没有频率成分上的偏差，因此得名为“白噪声”。

人类的听觉可以感知的声音范围大约在20Hz到20kHz之间，而白噪声包含了所有这个范围内的频率。

如果我们将这些频率的能量相等地混合在一起，就可以得到一种类似于“ssssss……”的连续声音信号，这就是白噪声。

二、白噪声的产生方式产生白噪声的方式有多种，其中最常见的是通过使用白噪声发生器。

这种发生器使用随机信号的方法来产生等能量频率的声波信号，从而形成白噪声。

在这个过程中，发生器会不断地产生随机信号，而随机信号的音高和音量都是根据一定的规律变化的。

正是由于这种变化方式的不确定性，所以才能保证白噪声中每个频率分量的能量相等。

另外，白噪声还可以通过数字信号处理的方式产生。

这种方法通常使用电脑进行模拟计算，通过将不同频率的信号按照一定比例叠加在一起，达到产生白噪声的目的。

三、白噪声的应用场景白噪声在很多场合都有着非常广泛的应用。

最常见的就是在睡眠环境中使用，以遮盖其他噪声的干扰，帮助人们更快地入睡。

除此之外，白噪声在音频工程中也经常被应用。

由于其等能量分布的特性，白噪声可以用来测试音响系统的频率响应，帮助音频工程师更好地调试音响设备。

此外，白噪声还可以用来测试传感器或其他电子设备的性能。

通过测量设备对白噪声的响应，来判断其对不同频率的信号的灵敏度和准确度，以便在实际应用中更好地使用。

四、总结综上所述，白噪声是一种由等能量频率组成的连续信号。

它的产生方式有多种，最常见的是通过使用发生器或数字处理等方式。

白噪声在睡眠环境中应用尤为广泛，同时也是音频工程和电子设备测试中不可或缺的一部分。

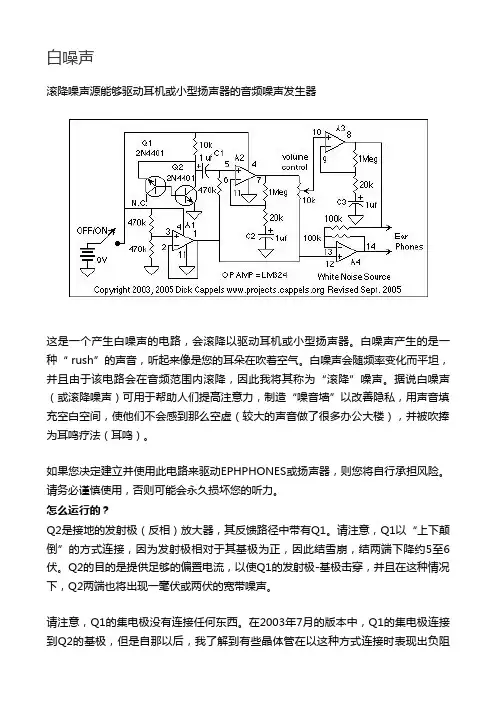
白噪声滚降噪声源能够驱动耳机或小型扬声器的音频噪声发生器这是一个产生白噪声的电路，会滚降以驱动耳机或小型扬声器。

白噪声产生的是一种“ rush”的声音，听起来像是您的耳朵在吹着空气。

白噪声会随频率变化而平坦，并且由于该电路会在音频范围内滚降，因此我将其称为“滚降”噪声。

据说白噪声（或滚降噪声）可用于帮助人们提高注意力，制造“噪音墙”以改善隐私，用声音填充空白空间，使他们不会感到那么空虚（较大的声音做了很多办公大楼），并被吹捧为耳鸣疗法（耳鸣）。

如果您决定建立并使用此电路来驱动EPHPHONES或扬声器，则您将自行承担风险。

请务必谨慎使用，否则可能会永久损坏您的听力。

怎么运行的？Q2是接地的发射极（反相）放大器，其反馈路径中带有Q1。

请注意，Q1以“上下颠倒”的方式连接，因为发射极相对于其基极为正，因此结雪崩，结两端下降约5至6伏。

Q2的目的是提供足够的偏置电流，以使Q1的发射极-基极击穿，并且在这种情况下，Q2两端也将出现一毫伏或两伏的宽带噪声。

请注意，Q1的集电极没有连接任何东西。

在2003年7月的版本中，Q1的集电极连接到Q2的基极，但是自那以后，我了解到有些晶体管在以这种方式连接时表现出负阻抗特性，因此对电路进行了修改，以从基极获取电流信号。

而不是收藏家。

A1是一个电压跟随器，用于缓冲由连接到其同相输入的两个470k电阻所产生的50％的电池电压。

50％的电压用作芯片上其他三个放大器的DC偏置电源。

A2和A3分别提供50倍的增益，总增益为2500倍。

LM324的开环增益与频率的关系图显示，带宽在大约5 kHz时截取了50X增益点，因此该滤波可以使噪声“变色”。

您选择的耳机或扬声器也会使信号变色。

您可以通过在一个或两个20k电阻器之间放置一个小电容器来获得一些带宽。

在我使用的耳机中，将一个.001 uF电容器跨接在一个20k电阻器中几乎是正确的。

通过在1兆欧的反馈电阻上放一些小电阻（例如5至100 pF），可以降低噪声。

计量经济学中白噪声的定义1. 引言嘿，朋友们，今天我们要聊聊一个看似复杂却其实挺有趣的话题，那就是“白噪声”。

你可能会想，“白噪声”是什么？是不是跟我耳朵里的嗡嗡声有关？哈哈，其实这个词在计量经济学中可是大有讲究的哦！就像生活中的小插曲一样，白噪声在数据分析中扮演着重要的角色。

那么，我们就来深入了解一下吧！2. 什么是白噪声？2.1 定义简单来说，白噪声是一种随机信号，具有恒定的功率谱密度。

听起来复杂对吧？其实可以理解为，它是没有规律可循的，像是你在街上听到的各种声音：汽车的喇叭声、路人的聊天声，这些声响一起混杂，听上去就像是一种背景噪音。

这个“背景噪音”在计量经济学中，通常被视为误差项，帮助我们理解数据中的不确定性。

2.2 特性白噪声有几个关键特性，首先，它是“零均值”的，意味着在长时间内，它的平均值为零。

想象一下，你每天的心情波动，有时开心得像个孩子，有时又低落得像个西红柿，但总体上，你的心情是有波动的，对吧？这就是白噪声的一个特点！其次，它的自相关性为零，也就是说，今天的噪声和明天的噪声没有关系，就像你今天吃了什么和明天的天气没啥关联一样。

3. 白噪声的应用3.1 在经济学中的作用那么，白噪声在经济学上有什么用处呢？哎呀，它可不是闲着没事做的！在建立经济模型时，经济学家常常会把白噪声用作随机干扰，帮助他们更好地解释观测数据。

比如说，某种商品的价格波动可能受多种因素影响，白噪声就能帮助我们捕捉那些无法预测的因素。

简单来说，就是给数据加点调味料，让分析更真实、更全面。

3.2 检测与识别当然，要识别白噪声并不是一件容易的事。

经济学家们通常会运用一些统计检验方法，比如自相关函数和单位根检验，来判断数据是否为白噪声。

说白了，就是看这些数据的“性格”，是不是像个无忧无虑的孩子，还是有些小心眼和阴暗面。

4. 结论说了这么多，白噪声其实并不神秘，它像是生活中的小插曲，虽然没有规律，但却在我们的分析中扮演着不可或缺的角色。