1.4阶跃函数和冲激函数

知识点1第一章第4节阶跃函数和冲激函数阶跃函数和冲激函数是控制工程和信号处理中常用的数学函数。

它们在描述系统的动态响应以及信号的特性时起到了重要的作用。

本文将详细介绍阶跃函数和冲激函数的定义、性质以及在实际应用中的意义。

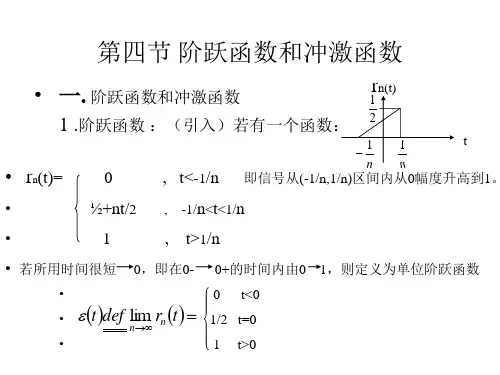
一、阶跃函数的定义和性质阶跃函数（Step Function）是一类常见的跃变函数，它在数学上用于描述其中一时刻突然跃变的情况。

阶跃函数通常被表示为u(t)，其中t 为自变量。

阶跃函数的定义如下：1,t≥0u(t)=0,t<0在定义中，当t≥0时，阶跃函数的取值为1；当t<0时，阶跃函数的取值为0。

阶跃函数的图像呈现为一个从0跃变到1的过程。

阶跃函数具有以下性质：1.阶跃函数u(t)在t=0的时刻不可导，因为它在该点没有斜率。

2.在t<0时，阶跃函数的值恒为0；在t>0时，阶跃函数的值恒为13.阶跃函数可用于表示信号的开关状态，如电路的打开和关闭。

二、冲激函数的定义和性质冲激函数（Impulse Function）是另一种重要的数学函数，它在数学上用于描述一个瞬间产生的脉冲信号。

冲激函数通常被表示为δ(t)，其中t为自变量。

冲激函数的定义如下：无穷,t=0δ(t)=0,t≠0在定义中，只有当t=0时，冲激函数的取值为无穷大；其余时刻冲激函数的取值都为0。

冲激函数的图像呈现为在t=0时的一个尖峰。

冲激函数具有以下性质：1.冲激函数δ(t)在t≠0的时刻都为0，只有在t=0时取值为无穷大。

2. 冲激函数是一个特殊的函数，它的积分等于1，即∫δ(t)dt=13.冲激函数可用于描述系统对瞬变信号的响应。

三、阶跃函数和冲激函数在实际应用中的意义阶跃函数和冲激函数在控制工程和信号处理中具有广泛的应用，主要包括以下方面：1.系统响应：阶跃函数和冲激函数可用于描述系统对不同类型输入信号的响应。

通过对系统在不同时刻的输出特性进行测量，可以得到系统的传递函数或冲激响应等重要参数。

冲激函数和阶跃函数的转化冲激函数和阶跃函数的转化，这个话题听起来有点高深，但其实它就像生活中的一些小把戏，懂得了就能玩得溜溜的。

你看，冲激函数就像一个活泼的小孩，蹦蹦跳跳地出现在某个时刻，呼啦一下就消失了，给你一个惊喜。

想象一下，一个小朋友在你身边喊：“哇，我来了！”然后就立刻安静下来，留下的只有那一瞬间的回声。

你是不是想起了上课时老师突然提问的那一刻？心里一惊，瞬间抓住了知识的精髓。

就是这个感觉，冲激函数就是那么一瞬间的强烈表达，时间上毫无余地。

而阶跃函数嘛，它就像是你家的门，关上了就是关上，打开了就永远开着。

想象一下，有个小门，早上刚打开，阳光洒进来，整个房间都亮堂堂的，那一刻的美好简直让人陶醉。

但是你知道，一旦这扇门打开，它就不会再关上了。

它从此在阳光下，静静地接受着生活的点滴。

阶跃函数就是这样，一开始静悄悄的，突然有那么一刻，哗啦一下变得热闹起来，之后就一直保持着这个状态，不再改变。

两者之间的关系就像茶和水的融合，有趣得很。

冲激函数虽然短暂，却能在短时间内释放出巨大的能量，像是给你一记响亮的耳光，让你瞬间清醒。

而阶跃函数则是从冲激函数的影响中悄悄生根发芽，像那一场春雨过后，小草悄悄钻出地面，逐渐长成一片绿意盎然的天地。

这俩家伙，看似没什么关联，其实就像朋友一样，互相依赖，缺一不可。

你也许在想，为什么冲激函数可以转化为阶跃函数呢？这就涉及到积分的魔法了。

想象一下，你有一个超大号的魔法杯，把冲激函数倒进去，一滴一滴地流，流着流着，最终这杯子就满了。

就是这个过程，冲激函数的瞬间释放通过积分变成了阶跃函数的持久存在。

就像你聚会时，总是要喝点饮料，慢慢喝着，最后这杯子就被你喝光了，那个喝光的过程其实就是冲激函数的魔力展现。

这其中还有很多小细节，像是时间轴的变化，影响着函数的表现。

冲激函数在时间上是一个极限的点，而阶跃函数则是一个不断延续的状态。

就像你在路边摊买的煎饼果子，热乎乎的摊上来，瞬间被你抢光，而吃完之后，饱腹感又长久地陪伴着你。