下载文档原格式
阶跃函数和冲激函数阶跃函数和冲激函数在分析线性电路过渡过程时，常使用一些奇异函数来描述电路中的激励或响应。
阶跃函数和冲激函数是两个最常用最重要的函数。
一、单位阶跃函数。
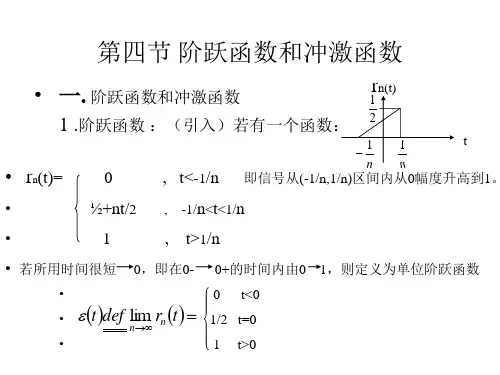
单位阶跃函数定义为：（式8-2-1）图8-2-1其波形如图8-2-1所示。
单位阶跃函数在处有跳变，是一个不连续点。
将单位阶跃函数乘以常数，就得到阶跃函数，又称为开关函数。
因为它可以用来描述电路中的开关动作，如图8-2-2所示。
图8-2-2所示电路在时刻开关S从1切换至2，那么一端口网络的入端电压就可用阶跃函数表示为：，如图8-2-2所示。
图8-2-2延时的单位阶跃函数定义为：（式8-2-2）其波形如图8-2-3所示，同样以图8-2-2为例，若时刻将开关S 从1切换至2，那么一端口网络的入端电压就可用延时阶跃函数表示为：。
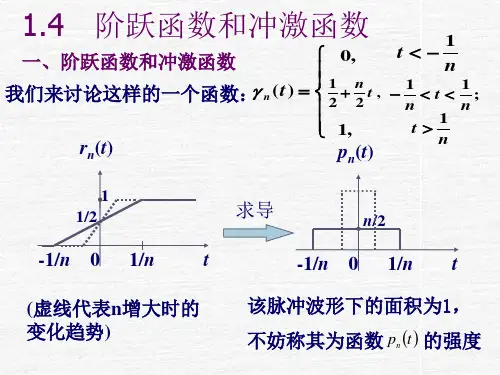
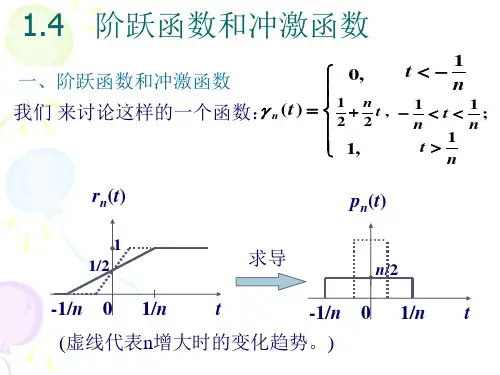
二、单位冲激函数单位冲激函数定义为：（式8-2-3）其波形如图8-2-5所示。
为了更好地理解单位冲激函数，先来看单位脉冲函数。
单位脉冲函数定义为：（式8-2-4）图8-2-5其波形如图8-2-5所示。
单位脉冲函数的宽度是，高度是，面积为1。
当脉冲宽度减小，其高度将增大，而面积仍保持为1。
当脉冲宽度趋于无限小时，其高度将趋于无限大，但面积仍然为1。
当脉冲宽度趋于零时，这时脉冲函数就成为单位冲激函数。
将单位冲激函数乘以常数K，就得到冲激强度为K的冲激函数，表示为。
延时的单位冲激函数定义为：（式8-2-5）其波形如图8-2-6所示。
图8-2-6冲激函数不是一般函数，属于广义函数，其更严格的定义可参阅有关数学书中的论述。
单位阶跃函数和单位冲激函数
分析动态电路中的电参量如电流、电压时，必须将其表示成一个随时间变化的函数。
实际上，在某个时刻，将开关闭合或断开，就可表示成一个函数。
1、Unit-step Function 单位阶跃函数
在t ＝t 0 时刻，将直流电压源U 0 与电路接通，可表示成：
定义一个名为“单位阶跃函数”：
函数在t ＝0 时，发生了跃变。
但为了问题的方便，认定：
ε( t ＝0－) ＝0
ε( t ＝0＋) ＝1
显而易见：
只要令t' ＝t －t0 即可。
上述直流电源的开关例子可表示为：
u( t )＝u0 ε( t －t0 )
一个幅度为I0 的矩形脉冲，可以用单位阶跃函数表示成：
2、Unit-impulse Function 单位冲激函数
单位冲击函数是另一个奇异函数，用δ(t) 表示，其定义为：
由定义可见，δ(t)只存在于t ＝0 时刻，故有：
δ(t)的性质有：
δ(t) 与ε(t) 的关系证明如下：
例如：如果在t ＝0 时刻，将恒压源U0 加到一个事先没有电荷的电容C 上，则有：
得结论：
充电前后，电容电压发生跃变0→U0；
流过电容的电流为冲激电流CU0δ(t)；
电容极板上的电荷量的跃变是有限的，为冲激电流的强度CU0。
又例如，如果在t ＝0 时刻，将恒流源I0 加到一个事先没有电流的电感L 上，则有：
得结论：
给电感接上恒流源前后，迫使电感电流发生跃变0→I0；
电感两端产生的感应电动势为冲激电压LI0δ(t)；
电感中的磁匝链数的跃变是有限的，为冲激电压的强度LI0。
