投资学第15章利率的期限结构

第15章利率的期限结构15.1 复习笔记利率期限结构，即不同到期期限债券利率之间的关系，通常用被称为收益率曲线的曲线图来描述。

1. 确定的期限结构长期债券收益率较高的原因有二：一是长期债券风险较大，需要较高的收益率来补偿利率风险；二是投资者预期利率会上升，因此较高的平均收益率反应了对债券后续寿命期的高利率预期。

（1）债券定价给定期限的利率称为短期利率。

利用不同期限的短期利率对债券进行贴现可以得到债券的价格。

利用债券的价格，可计算出每种债券的到期收益率。

收益率是单利，它等于相对于债券价格的债券支付额的现值。

虽然利率可随时间变化，但各期的到期收益率均以“平均”利率计算，以贴现所有各期的债券支付。

不同期限的到期收益率可以构成收益率曲线。

零息票债券的到期收益率有时也称为即期利率，即今日对应于零期时的利率。

到期收益率实际上是每一时期利率的几何平均值。

（2）分离债券和息票债券的定价零息票债券的价格可以通过用债券到期时的即期利率对债券票面价值贴现后得到。

可以把息票债券的每一次付息从结果上视为各自独立支付的零息票债券，它们可以独立地被估价。

息票债券的总价值就是其每一次现金流价值的总和。

债券交易者经常要区分零息票债券和息票支付债券的收益曲线。

纯收益曲线反映了零息票债券的到期收益和到期时间之间的关系。

（3）持有期收益（holding period yield, HPY ）在一个简单的没有不确定性因素的世界中，任何期限的债券一定会提供相同的收益率。

实际上，尽管不同的债券有不同的到期收益率，但每一种债券提供的未来一年的收益率将等于这一年的短期利率。

持有期收益指在一定时期内投资的总收益，包括各种来源的收入。

其计算公式如下：投资的期初价值投资的期末价值HPR其计算得出的值总是大于或等于0, 即它不可能为负值。

如果该值大于1.0表明财富增加，这意味着持有期的收益率为正；如果该值小于1.0表明财富减少，这意味着在持有期的收益率为负；如果该值等于0表明投资损失殆尽。

利率及利率期限结构利率是指借贷双方的利益关系中由借款方向贷款方支付的一种代价，是资金交易中的重要因素之一、利率的大小和变动对个人、企业和国家经济发展都有很大的影响。

利率期限结构是指一定时期内不同借贷期限的利率水平之间的关系。

在市场经济中，利率期限结构反映了市场上不同期限的借贷利率的变化和相互关系。

对于借款人和投资人来说，利率期限结构对选择借贷和投资期限有重要的指导作用。

利率期限结构通常呈现出以下几种形态：正常的正斜率、倒斜率和平坦的水平。

正常的正斜率是指较短期限的借贷利率低于较长期限的借贷利率，这是由于长期借贷存在更高的风险和不确定性。

倒斜率则是指较短期限的借贷利率高于较长期限的借贷利率，这通常是一种非常罕见的情况，可能出现在经济不稳定或信贷紧缩的情况下。

平坦的水平是指不同期限的借贷利率基本上相等或非常接近，这可能是市场对未来的经济发展没有明确的预期，或者是货币储备过剩导致无法有效地分配资金。

利率期限结构的研究对于各类金融机构和市场参与者非常重要。

首先，它对于市场参与者的资金配置和投资决策有重要的指导作用。

如果利率期限结构保持正常的正斜率，那么短期投资可能会取得较好的回报，而长期投资可能会有较高的风险。

反之，如果利率期限结构出现倒斜率，那么短期投资可能会带来更大的风险和不确定性。

其次，利率期限结构也对货币政策和金融稳定具有很大的影响。

利率期限结构的演变可以反映市场对未来经济发展的预期，央行可以通过利率调整来引导市场的风险偏好和资金配置。

此外，利率期限结构的变动也可能反映市场对货币政策的反应，央行可以通过观察和分析利率期限结构的变化来评估货币政策的效果和市场预期。

最后，利率期限结构的变动也对实体经济有着重要的影响。

利率的大小和变动直接关系到个人、企业和国家的借贷成本和投资回报率。

如果利率期限结构保持正常的正斜率，那么企业可以通过选择不同期限的借贷来降低成本或提高回报。

而如果利率期限结构出现倒斜率，那么企业可能面临借贷成本上升和资金获取困难的问题。

简述利率期限结构理论利率期限结构理论是描述不同期限的利率之间的关系的理论模型。

这个理论对投资者和借款者在决策投资和借贷时如何选择期限提供了一种理论解释。

在金融市场中，利率期限结构理论对于决策者和政策制定者来说具有重要的意义，因为它可以影响金融市场的利率设定和资源配置。

利率期限结构理论的基本观点是，不同期限的利率（即短期利率、中期利率和长期利率）之间存在一种关系，这种关系可以被称为利率期限结构。

根据这个理论，长期债券的利率应该高于短期债券的利率，因为长期债券面临的风险和不确定性更高。

此外，利率期限结构理论还表明，短期利率和长期利率之间的差异可以被用来预测经济的未来走势。

利率期限结构理论的几个核心假设是利率的期望假设、流动性偏好假设和风险偏好假设。

首先，利率期限结构理论假设投资者有一个关于未来短期利率的预期，这个预期反映了市场参与者对未来经济发展的看法。

根据这个假设，长期利率是由短期利率的预期所决定的，如果投资者预期短期利率会上升，那么长期利率也会上升。

其次，利率期限结构理论假设投资者更倾向于持有短期债券而不是长期债券，这被称为流动性偏好。

这种偏好是由投资者对流动性的需求和风险规避的意愿所决定的，因为短期债券在未来的利率波动中更易于购买或出售。

最后，利率期限结构理论假设风险偏好是影响投资者选择债券期限的因素之一、根据这个假设，投资者更愿意购买短期债券，因为长期债券面临更多的风险和不确定性。

利率期限结构理论主要有两种解释：期望理论和流动性偏好理论。

期望理论认为，利率期限结构是由市场参与者对未来利率的期望所决定的。

如果投资者预期利率将上升，那么短期利率将高于长期利率。

流动性偏好理论则认为，投资者更喜欢购买短期债券，因为短期债券具有更高的流动性和可变性。

利率期限结构理论对金融市场和政策制定者有重要影响。

首先，理解利率期限结构的变化和因素可以帮助投资者和借款者在决策投资和借贷时选择合适的期限。

其次，利率期限结构可以提供对未来经济走势和利率变动的预测。

（二）利率的期限结构债券的期限和收益率在某一既定时间存在的关系就称为利率的期限结构，表示这种关系的曲线通常称为收益曲线。

利率期限结构主要讨论金融产品到期时的收益与到期期限这两者之间的关系及变化。

一般而言，随着利率水平的上升，长期收益与短期收益之差将减少或变成负的。

也就是说，当平均利率水平较高时，收益曲线为水平的（有时甚至是向下倾斜的），当利率较低时，收益率曲线通常较陡。

收益率曲线的三种特征：不同期限的债券，其利率经常朝同方向变动。

利率水平较低时，收益率曲线经常呈现正斜率；利率水平较高时，收益率曲线经常出现负斜率。

收益率曲线通常为正斜率。

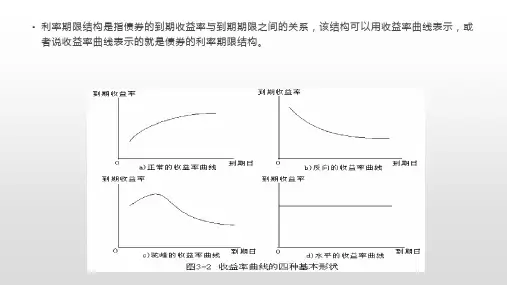
收益曲线的表现形态有：（1）正常的收益曲线（上升曲线），即常态曲线，指有价证券期限与利率呈正相关关系的曲线；（2）颠倒的收益曲线（下降曲线），指有价证券期限与利率呈负相关关系的曲线。

收益曲线是指那些期限不同、却有着相同流动性、税率结构与信用风险的金融资产的利率曲线。

金融资产收益曲线反映了这样一种现象，即期限不同的有价证券，其利率变动具有相同特征。

曲线的这些特征将通过利率期限结构理论予以解释。

（记住三个理论，理解其含义）1、纯预期理论纯预期理论把当前对未来利率的预期作为决定当前利率期限结构的关键因素。

该理论认为，市场因素使任何期限长期债券的收益率等于当前短期债券收益率与当前预期的超过到期的长期债券收益率的未来短期债券收益率的几何平均。

如果买卖债券的交易成本为零，而且上述假设成立，那么投资者购买长期债券并持有到期进行长期投资时，获得的收益与同样时期内购买短期债券并滚动操作获得的收益相同。

(1)纯预期理论1、该理论把当前对未来的预期是决定当前利率期限结构的关键因素。

2、该理论认为，市场因素使任何期限长期债券的收益率等与当前短期债券收益率与当前预期的超过到期的长期债券收益率的未来短期债券收益率的几何平均。

3、如果买卖债券交易成本为零，上述假设成立的话，该理论结论是：投资者购买长期债券并持有到期所获得的收益与在同样时期内购买短期债券并滚动操作获得的收益相同。