小学数学知识体系

小学数学知识体系数学内容结构表一、数与代数㈡数的运算㈢常见的量㈣探索规律二、空间与图形㈡测量㈢图形与变换㈣图形与位置三、统计与概率㈡可能性四、实践与综合应用㈠数学广角㈡综合实践活动现行《大纲(试用修订版)》在“实践活动”的安排上要求“结合有关教学内容和学生生活实际，每学期至少安排一次数学实践活动”。

《标准》设置“综合实践活动”这种新的学习形式，为学生提供实践活动的机会，强调与他人合作并发挥自己在集体中的作用，获得积极的数学学习情感，目的是为了培养和发展学生的创新意识和实践能力。

第一学段和第二学段分别以“实践活动”和“综合应用”安排内容，实践活动的课时比例与现行《大纲(试用修订版)》相比，从量上有提高，从质上有变化。

㈢解决问题从实质上说，“解决问题”教学的目标与“应用题”教学是相同的，都是让学生学会应用所学的数学知识解决简单的实际问题。

但是，在编排上“解决问题”教学与原“应用题”有着很大的不同。

以前的“应用题”是独立于其他知识单独编排的，与其他知识的结合不够紧密，另外，教师们通过长期的实践，在“应用题”教学中积累了丰富的经验，对应用题的解题方法形成了固定的格式，这对于学生掌握解题技巧确实很有帮助。

但是当学生掌握了这种解题模式，就不去分析数量关系了，使得解应用题变成了机械的训练，也就失去了“应用题”教学培养学生思维能力、应用意识等的作用。

实验教材中，“解决问题”的编排是融于其他知识中的，在学生掌握了相关的数学知识后，给学生创设现实的具体情境，让学生运用这些知识来解决一些相应的实际问题。

比如第一单元和第四单元，就是结合计算知识教学应用这些知识解决相应的实际问题；又如在空间与图形的有关单元，教学利用这些知识解决相应的实际问题；等等。

这样就使解决问题教学和各部分数学知识的教学有机的结合在一起，同时从现实情境中提出问题还可以让学生体会数学在实际生活中的应用。

“解决问题”的教学目标是培养学生提出问题、分析问题、解决问题的能力，体会数学知识在解决实际问题中的作用。

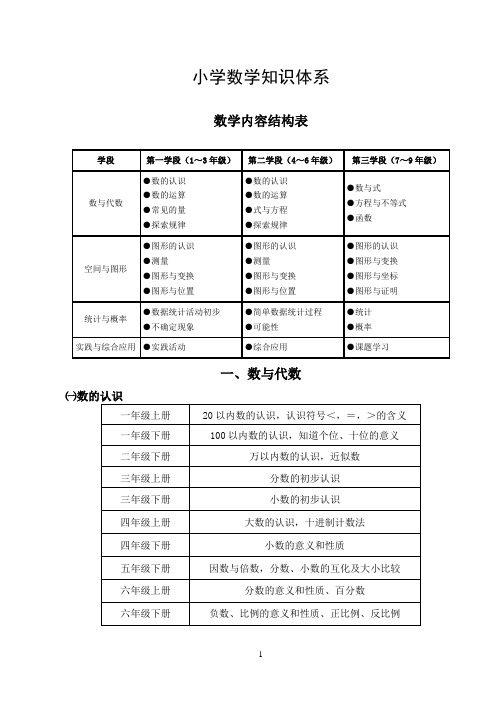
小学数学知识体系小学数学知识体系数学内容结构表学段第一学段（1～3年级）数的认识与代数：这一学段的内容主要是数的认识和代数。

学生将研究20以内、100以内和万以内数的认识，以及分数和小数的初步认识。

他们还将研究符号＜，＝，＞的含义。

数的运算：此外，学生还将研究数的运算，包括10以内加减法，20以内进位加法，20以内退位减法，100以内的加法和减法，表内乘法，表内除法，万以内的加法和减法，估算，有余数的除法等。

图形与空间：学生将研究图形的认识和空间的概念。

他们将研究探索规律，测量，图形与变换，图形与位置以及统计与概率。

第二学段（4～6年级）数的认识：在第二学段，学生将进一步研究数的认识，包括大数的认识，十进制计数法，小数的意义和性质，因数与倍数，合数和质数等。

数的运算：学生将研究数的运算，包括分数、小数的互化及大小比较，比和按比例分配，负数的初步认识，百分数，正比例和反比例等。

图形与空间：此外，学生还将研究图形的认识，测量，图形与变换，图形与位置以及简单数据统计过程和可能性。

第三学段（7～9年级）数与代数：在第三学段，学生将研究数与式，方程与不等式，函数等代数概念。

图形与空间：此外，学生还将研究图形的认识，图形与变换，图形与坐标，图形与证明以及统计和概率等知识。

实践活动：学生将通过课题研究实践和综合应用，进行实践活动，提高他们的数学能力。

总体来说，小学数学知识体系包括数的认识与代数，数的运算，图形与空间以及实践活动等方面，帮助学生逐步建立完整的数学知识体系。

1.学会读时钟和计算时间认识小时、分钟、和秒钟，知道1小时等于60分钟，1分钟等于60秒钟。

能够读写时间，例如几点几分。

2.重量和单位换算认识XXX，以及不同的进率和单位换算。

3.日期和时间的关系认识年、月、日，了解它们之间的关系。

4.代数方程和规律学会用字母表示数、等式、方程、解方程。

探索给定事物中隐含的规律或变化趋势。

5.图形的认识和分类辨认常见的立体图形和平面图形，并能分类。

小学数学全知识体系本文整理了，小学阶段数学所有相关定理、公式、数量关系、基本概念，辅助毕业考、择校考复习。

一、各年级知识体系一年级：九九乘法口诀表；基础加减乘。

二年级：完善乘法口诀表；除混合运算；基础几何图形。

三年级：乘法交换律；几何面积周长；时间量及单位；路程计算；分配律；分数小数。

四年级：线角自然数整数，素因数、梯形、对称；分数小数计算。

五年级：分数、小数乘除法，代数、方程及平均数，比较大小、变换，图形面积、体积。

六年级：比例、百分比、概率，圆、扇、圆柱及圆锥。

二、小学阶段面积、体积公式。

1、正方形C周长S面积a边长周长＝边长×4C=4a面积=边长×边长S=a×a2、正方体V体积a棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4、长方体V体积s面积a长b宽h高表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)体积=长×宽×高V=abh5、三角形s面积a底h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形s面积a底h高面积=底×高s=ah7、梯形s面积a上底b下底h高面积=(上底+下底)×高÷2s=(a+b)×h÷28、圆形S面积C周长π直径d半径r周长=直径×π=2×π×半径C=πd=2πr面积=半径×半径×π=πr29、圆柱体体积V高h底面积S底面半径r底面周长C侧面积=底面周长×高=S侧=ch，表面积=侧面积+底面积×2=S表=S侧+2S底体积=底面积×高，体积＝侧面积÷2×半径10、圆锥体体积V高h底面积S底面半径r体积=底面积×高÷3=S底×h÷3三、运算法则1、加法交换律：两数相加交换加数的位置，和不变。

小学数学知识体系第一部分数与代数①数的意义:整数、小数、分数、百分数的有关概念。

②数的读法和写法。

会认读写大数目的数，会比较数的大小，会用万、亿为单位表示大数。

③小数、分数、百分数、比的关系与互化。

④小数、分数的基本性质。

⑤百分数与折扣、成数的关系。

⑥小数点位置移动引起小数大小变化的规律。

⑦数的整除。

自然数、因数与倍数，奇数与偶数，质数与合数，2、3、5倍数的特征，找两个数的最大公因数和最小公倍数，分解质因数，最大公因数与最小公倍数的应用。

⑧初步认识负数，会用负数表示日常生活中的问题。

在掌握这些概念的同时，还要注意使学生掌握一些必备的技能:会读写大数目的数，会用万、亿为单位表示大数；会进行小数、分数、百分数、比的互化；因数与倍数知识中的相关技能，初步认识负数。

①四则运算的意义及计算方法。

②积、商的变化规律。

③运算定律及其应用，理解运算定律，能应用运算定律进行一些简便计算。

④估算。

在解决具体问题的过程中，能选择合适的估算方法并进行估算。

⑤四则混合运算。

体会四则混合运算意义，掌握运算顺序，能正确进行整数和小数，整数和分数四则混合运算（一般不超过三步）。

⑥探索简单的数学计算规律。

⑦用整数、小数解决问题，用分数、百分数解决问题（包括折扣、成数）。

学生估算、四则混合运算能力达到一定的水平，解决问题中要注意培养学生综合运用知识解决简单实际问题的能力。

①用字母表示数。

掌握用字母表示运算定律、计算公式、计算法则和规律，能够在具体的情境中用字母表示数量关系，会根据字母所取的值，求含有字母式子的值。

②方程。

理解方程的意义，理解等式的基本性质，掌握方程的解法（包括比例方程）和验算方法，会解方程。

③列方程（算术方法）解文字题④列方程解决问题。

会列方程解决一些简单的实际问题（要增补内容）。

通过用字母表示数、解方程、列方程解决一些简单的实际问题，来落实关于“式与方程”的训练目标。

①长度、面积、体积、容积、时间、质量等计量单位的进率。

小学到大学全部数学知识点一、小学数学知识点1. 数的认识和比较：数的读法和书写、数的顺序、数的比较、正数和负数的认识。

2. 加法和减法：加法和减法的概念、加法和减法的运算方法、进位和退位的原理。

3. 乘法和除法：乘法和除法的概念、乘法和除法的运算方法、乘法口诀表、倍数和约数的认识。

4. 分数：分数的认识、分数的加减乘除、分数的计算、分数的比较大小。

5. 小数：小数的认识、小数的加减乘除、小数的计算、小数与分数的转化。

6. 百分数：百分数的认识、百分数的加减乘除、百分数与分数、百分数与小数的转化。

7. 二维几何图形：常见二维几何图形的认识、图形的属性和特征、图形的分类和命名。

8. 三维几何图形：常见三维几何图形的认识、图形的属性和特征、图形的分类和命名。

9. 单位换算：长度、重量、容量单位的换算、常见单位的认识。

10. 时间和日历：常见的时间单位、时间的读写、日历的认识、日期的计算。

二、初中数学知识点1. 代数初步：代数的基本概念、代数式的读写、代数式的展开和合并、等式和方程。

2. 平面图形：点、线、面的基本概念、三角形、四边形、多边形的性质、相似和全等。

3. 分数与小数：分数和小数的相互转化、分数和小数的运算、分数方程与分数不等式。

4. 比例与利益：比例的概念、比例的计算、利息和利润的计算。

5. 数据与概率：统计图表的制作和分析、概率的基本概念、简单事件的概率计算。

6. 空间几何：空间几何图形的认识和刻画、立体图形的表面积和体积计算。

7. 三角函数：正弦、余弦、正切、三角函数的计算和应用。

8. 整式与分式：整式的加减乘除、分式的加减乘除、整式方程与分式方程。

9. 质因数与倍数：质因数分解、最大公约数和最小公倍数的计算。

10. 方程与不等式：一元一次方程与一元一次不等式的解法、一元二次方程与一元二次不等式的解法。

三、高中数学知识点1. 函数与方程：函数的概念和性质、函数的图像和性质、方程的根与解法。

小学,初中,高中,大学数学知识体系概要知乎数学是一门广泛应用于各个学科领域的学科，从小学到大学，数学知识的学习一直贯穿着我们的学业生涯。

本文将概述小学、初中、高中和大学阶段的数学知识体系，让我们一起来了解数学知识的发展脉络。

小学数学知识体系概要小学数学主要培养学生的数学思维能力和基本的运算技能。

在小学阶段，数学教学注重培养学生的逻辑思维和问题解决能力。

以下是小学数学知识体系的概要：1. 数的认识和运算：学生通过认识自然数、整数、分数、小数等来了解数的概念，学习加减乘除等基本运算。

2. 几何图形：学生学习平面图形和空间图形的名称、性质和构造方法，包括点、线、面、角等。

3. 基本量和单位：学生通过学习长度、面积、体积、重量、时间等基本量的认识和使用，掌握常用的度量单位。

4. 数据的收集和整理：学生通过调查和统计活动，学习如何收集数据，并利用表格、图表等方式进行整理和分析。

初中数学知识体系概要初中数学是小学数学的延伸和拓展，主要培养学生的数学思维和推理能力。

以下是初中数学知识体系的概要：1. 代数与方程：学生学习代数表达式的表示和计算方法，掌握一元一次方程、一次不等式等的解法。

2. 几何与证明：学生学习几何图形的性质、相似、全等等概念，并通过证明方法来验证结论。

3. 函数与图像：学生学习函数的概念和性质，并通过函数图像来理解函数的变化规律。

4. 统计与概率：学生通过数据的统计和概率的计算，了解数据的规律和不确定性的量化方法。

高中数学知识体系概要高中数学是数学知识的深化和扩展，培养学生的抽象思维和推理能力。

以下是高中数学知识体系的概要：1. 初等数学：学生通过学习数与式、方程与不等式、函数与图像等内容，掌握初等数学的基本概念和方法。

2. 高等数学：学生学习微积分、数列与数学归纳法、几何与向量、概率论与数理统计等内容，为日后大学数学的学习打下基础。

3. 数学思想与方法：学生通过学习数学史、证明方法、数学建模等内容，培养数学思维和创新意识。