QC七大手法之排列图(第一讲)

QC七大手法引言质量控制(QC)是一种系列的活动，旨在确保产品或效劳符合预期的质量标准。

为了有效地进行QC，人们使用了各种手法和方法。

本文将介绍QC的七大手法，包括直方图、散点图、排列图、Pareto图、因果图、控制图和检查表。

通过运用这些手法，可以发现和解决质量问题，从而提高产品和效劳的质量水平。

直方图直方图是一种用来展示数据分布情况的图形，特别适用于连续型数据。

它将数据按照一定的区间划分，并将每个区间内的数据数量用柱状图表示。

通过直方图，我们可以直观地了解数据的分布情况，包括中心位置、离散程度等。

在QC中，直方图可以帮助我们判断一个过程是否稳定，并找出造成质量问题的原因。

散点图是用来展示两组数据之间关系的图形。

它将一组数据以点的形式表示在二维坐标系中，并通过点的位置来表示数据之间的关联性。

通过观察散点图，我们可以判断是否存在某种线性关系、相关性或者异常值。

在QC中，散点图可以帮助我们找出可能导致质量问题的因素，并进行相应的调整和改良。

排列图排列图是一种用来展示数据之间大小关系的图形。

它将数据按照一定的顺序排列，并以不同的长度或高度表示数据的大小。

通过排列图，我们可以清晰地看到数据之间的相对大小，从而找出可能存在的问题和瓶颈。

在QC中，排列图通常用于分析产品或效劳中的瑕疵程度，并制定相应的改良措施。

Pareto图是一种用来展示问题因素的重要性程度的图形。

它将问题因素按照重要性从大到小进行排序，并以条形图的形式表示。

通过Pareto图，我们可以清晰地看到哪些问题因素对整体质量影响最大，从而有针对性地进行改良。

在QC中，Pareto图被广泛应用于问题分析和改良活动中。

因果图因果图是一种用来展示问题因果关系的图形。

它利用图形化的方式将问题的各种可能原因进行分类和整理，并展示它们之间的关系。

通过因果图，我们可以分析问题的根本原因，从而采取相应的对策和改良措施。

在QC中，因果图常常用于问题解决和质量改良的过程中。

QC七工具之排列图排列图（Pareto Plot）又叫帕累托图、8020图等。

它是将质量改进项目从最重要到最次要顺序排列而采用的一种图表，它在形式上是由两张图表组合而成的，一个是标记每个项目发生频数的柱状图，另一个是标记项目累计百分比的折线图。

排列图的主要用途有：按重要顺序显示出每个质量改进项目对整个质量问题的影响程度；识别进行质量改进的机会。

图一常规排列图图一显示的就是一家生产电子产品的公司在对近期生产中发生的缺陷记录进行统计，并整理成的排列图形式。

显而易见，“Missing Screws”出现的频次显著地高于“Missing Clips”、“Leaky Gaskets”等其他缺陷，应该抓住这个机会，将它作为质量改进的主要方向，值得对它作深入的调查研究与分析。

应用排列图时应当注意到：绘制排列图的主要目的，是为了剔除次要的“多数”，找到关键的“少数”。

因此，当你发现柱状图下降趋势缓慢，头部项目和尾部项目之间的落差不大时，可以尝试用以下方法调整：1. 柱状图的纵坐标不用“件数”来表示，而改用其他可量化的指标（如“金额”等）来表示。

2．横坐标不用“缺陷”来表示，而改用其他分类指标（如“产品类型”等）来表示。

3．增加分层变量（如“时间”等），绘制“分层排列图”Stratified Pareto Plot。

所有这些方法的目的都是为了更快速、更准确地在杂乱无章的数据中发现主要矛盾。

JMP软件深知实际工作中这些细节的重要性，因此在其“Pareto图”平台上都提供了相应的操作选项。

例如，如果我们在记录缺陷时记录了日期（OCT1、OCT2或OCT3）和设备清洗状态（before或after），就可以将一张反映整体的排列图细化为6（=3*2）张乃至更多、体现两个维度类别信息的分层排列图（如图二）。

这样就可以更加清晰地观察不同日期、不同设备清洗状态下的缺陷分布情况，便于我们发现关键问题，同时也可用于进行不同条件下的产品质量对比。

品管七大手法：检查表——收集、整理资料；排列图——确定主导因素；散布图——展示变量之间的线性关系；因果图——寻找引发结果的原因；分层法——从不同角度层面发现问题；直方图——展示过程的分布情况；控制图——识别波动的来源；一、检查表（数据采集表）系统地收集资料和累积数据，确认事实并对数据进行粗略的整理和简单分析的系统的统计图表。

注意几点：用在对现状的调整，以备今后作分析；对需调查的事件或情况，明确项名称；确定资料收集人、时间、场所、范围；数据汇总统计；必要时对人员的能力进行培训；二、排列图用从高到低的顺序排列的一组矩形表示各原因出现频率高低的一种图表。

原理是80%的问题仅来源于20%的主要原因。

注意几点明确问题和现象；寻找不良的情况统计数据；频率计算和累计；对频率从高到低的顺序排列；三、散布图研究成对出现的不同变量之间相关关系的坐标图。

注意几点：收集足够的数据，至少30对；横坐标表示数据（原因），纵坐标表示因变量（结果）；正确判断变量之间的关系模式；因果图的后续工作，提供直观的相关性验证；四、因果图用于寻找造成问题产生的原因，即分析原因与结果之间关系的一种方法。

注意几点：充分组织人员全面观察，从人、机、料、法、环、测方面寻找；针对初步原因展开深层的挖掘；记下制图部门和人员、制图日期、参加人员；五、分层法按照一定的类别，把记录收集到的数据加以分类整理的一种方法。

注意几点：确定分层的类别和调查的对象；设计收集数据的表格；收集和记录数据；整理资料并绘制相应图表；比较分析和最终的推论；用于分析和掌握数据的分布状况，以便推断特性总体分布状态的一种统计方法。

注意几点：确定过程特性和计量标准值；收集数据，必须是计量值数据；数据针对一个范围时期收集至少50-100个；确定积差、分组数、分组组界、组间距；作次数分配表控制图是用于分析和控制过程质量的一种方法。

控制图是一种带有控制界限的反映过程质量的记录图形，图的纵轴代表产品质量特性值(或由质量特性值获得的某种统计量)；横轴代表按时间顺序(自左至右)抽取的各个样本号；图内有中心线(记为CL)、上控制界限(记为UCL)和下控制界限(记为LCL)三条线注意几点：确定产品型号、工序名称、品质特性。

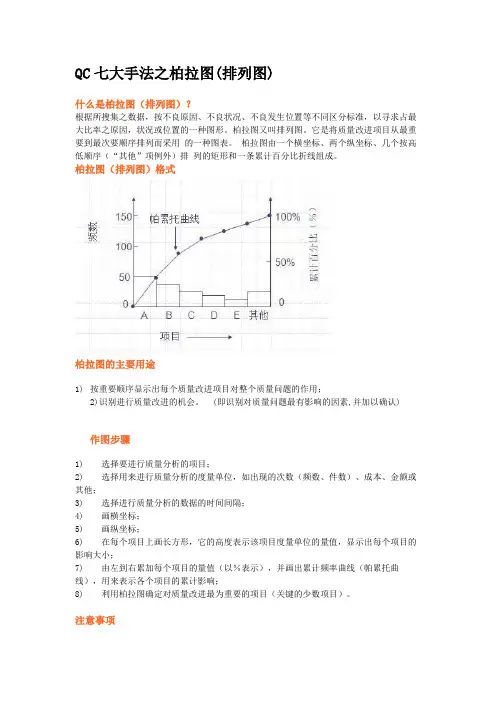
QC七大手法之柏拉图(排列图)什么是柏拉图（排列图）？根据所搜集之数据，按不良原因、不良状况、不良发生位置等不同区分标准，以寻求占最大比率之原因，状况或位置的一种图形。

柏拉图又叫排列图。

它是将质量改进项目从最重要到最次要顺序排列而采用的一种图表。

柏拉图由一个横坐标、两个纵坐标、几个按高低顺序（“其他”项例外）排列的矩形和一条累计百分比折线组成。

柏拉图（排列图）格式柏拉图的主要用途1)按重要顺序显示出每个质量改进项目对整个质量问题的作用；2)识别进行质量改进的机会。

(即识别对质量问题最有影响的因素,并加以确认)作图步骤1) 选择要进行质量分析的项目；2) 选择用来进行质量分析的度量单位，如出现的次数（频数、件数）、成本、金额或其他；3) 选择进行质量分析的数据的时间间隔；4) 画横坐标；5) 画纵坐标；6) 在每个项目上画长方形，它的高度表示该项目度量单位的量值，显示出每个项目的影响大小；7) 由左到右累加每个项目的量值（以％表示），并画出累计频率曲线（帕累托曲线），用来表示各个项目的累计影响；8) 利用柏拉图确定对质量改进最为重要的项目（关键的少数项目）。

注意事项1) 一般来说，关键的少数项目应是本QC小组有能力解决的最突出的一个，否则就失去找主要矛盾的意义，要考虑重新进行项目的分类；2) 纵坐标可以用“件数”或“金额”等来表示，原则是以更好地找到“主要项目”为准；3) 不太重要的项目很多时，横轴会变得很长，通常都把这些列入“其他”栏内，因此“其他”栏总在最后；4) 确定了主要因素，采取了相应的措施后，为了检查“措施效果”，还要重新画出排列图。

应用实例某公司QC小组在2001年对其电子产品的用户反馈单进行了统计，整理后的资料，如下：从图中可看出，该公司产品的“插头焊接缺陷”应作为“质量改进”的主要对象，应对它作进一步的调查研究与分析。

以上是对品质管理工具之一的柏拉图的介绍，其中柏拉图遵循二八原则，即：1、80%的问题由20%的原因引起；2、80%的索赔发生在20%的生产线上；3、80%的销售额由20%的产品带来；4、80%的品质成本由20%的品质问题造成；5、80%的品质问题由20%的人员引起。

品管（QC）七大手法之排列图(Pareto Diagram,柏拉图)什么是排列图法定义:根据所搜集之数据,按不良原因、不良状况、不良发生位置等不同区分标准,以寻求占最大比率之原因,状况或位置的一种图形.排列图法，又称主次因素分析法、柏拉托（Pareto）图法，它是找出影响产品质量主要因素的一种简单而有效的图表方法。

1897年意大利经济学家柏拉图（1848---1923）分析社会经济结构，发现80%的财富掌握在20%的人手里，后被称“柏拉图法则”。

1907年美国经济学家劳伦兹使用累积分配曲线描绘了柏拉图法则，被称为“劳伦兹曲1930年美国品管泰斗朱兰博士将劳伦兹曲线应用到品质管理上。

排列图是根据“关键的少数和次要的多数”的原理而制做的。

也就是将影响产品质量的众多影响因素按其对质量影响程度的大小，用直方图形顺序排列，从而找出主要因素。

其结构是由两个纵坐标和一个横坐标，若干个直方形和一条折线构成。

主要纵坐标表示不合格品出现的频数（出现次数或金额等），次要纵坐标表示不合格品出现的累计频率（如百分比表示)，横坐标表示影响质量的各种因素，按影响大小顺序排列，直方形高度表示相应的因素的影响程度（即出现频率为多少），折线表示累计频率（也称帕累托曲线）。

通常累计百分比将影响因素分为三类：占0%～80%为A类因素，也就是主要因素；80%～90%为B类因素，是次要因素；90%～100%为C类因素，即一般因素。

由于A类因素占存在问题的80%，此类因素解决了，质量问题大部分就得到了解决。

为了方便理解，下图是对某酒杯制造厂对某日生产中出现的120个次品进行统计，做出排列图，如下图所示：帕累托图排列图的作用 1、作为降低不良依据。

2、决定改善的攻击目标。

3、确认改善效果。

4、用于发现现场的重要问题点 5、用于整理报表或记录。

6、可作不同条件的评价。

排列图的使用排列图的使用要以层别法为前提，将层别法的项目从大到小的进行排列，再加上累积值的图形。

QC七大工具资料2011-10-20 10:36|发布者: 小编H|查看: 1762|评论: 42|原作者:lhjie2008|来自: 摘要: 第一种手法：排列图排列图是指：将问题的原因或是状况进行分类，然后把所有的数据由大到小排列后，所绘出的累计柱状图。

它是由意大利经济学家巴雷特（Vifredo Pareto ...第一种手法：排列图排列图是指：将问题的原因或是状况进行分类，然后把所有的数据由大到小排列后，所绘出的累计柱状图。

它是由意大利经济学家巴雷特（Vifredo Pareto）在分析社会财富分配状况时发现的，大部分的财富集中在少部分手中，为此他设计出能够反映这种规律的图，所以也有人称为“巴雷特图”或“柏拉图”，后来有美国人裘兰（Joseph Juran）博士加以推广使用。

1．作用：在现场众多的不良品问题中，找出关键的前几名，以便决定今后管理工作的重点。

2．作成方法：①列出所有不良项目，并收集相应时期的数据。

②按数据大小，排列不良项目。

③设定坐标系，填上坐标值，坐标值要能反映蛭大、最小数据左纵坐标为不良数据，右纵坐标为不良率累计百分比，横坐标为不良项目。

④按数据多少，绘出术状图，并在其X轴下方记入项目。

⑤计算各项目所占比例，累计后将其值记入坐标系中。

⑥将各比例点连接起来，一直到100%。

⑦记和图名、作成者、长、作成时间等相关内容。

例如，某厂T550录音机1998年3月份，工序内不良的发生情况如下：NO 不良项目数量累计1 抖晃 87 41.00%2 音量小 42 60.80%3 R键不锁定 31 75.50%4 K盖伤痕 21 85.40%5 共振 13 91.50%6 播音失真 10 96.20%7 其他 8 100.00%根据以上数据，可以画得如下排列图：通过排列图，可以很直观地看出，头4位不良，占了总不良的80以上，根据抓大放小、针对关键的原则，1998年4月起的主要管理重点，应为头4项，而其他3项则暂不予理会。

QC七大手法第一节: 数据的基本常识及其特性一. 质量管理常用的七种工具: 排列图. 因果分析图. 调查表. 直方图. 散布图. 管制图. 数据分层法.质量管理的"二图一表": 排列图. 因果分析图及我国传统的对策措施表.二. 数据的分类:1.计量值数据:可以连续取值的数据.如长度,重量等2.计数值数据:不能连续取值的,只能以个数计算的数据.它可细分为计件值数据和计点值数据3.相对数(即分数): 分子 / 分母当分子为计数值时, 则相对数为计数值; 当分子为计量值时, 则相对数为计量值.三. 数据的几个重要特征数数据的特征数可分为两类:1.表示数据集中位置的特征数.如平均数.中位数及中程众数等.2.表示数据离散的特征数.如极差.平均偏差.偏差平方和.方差和标准差等.第二节: QC七大手法一. 查检表(调查表/分析表/核对表):1. 何谓查检表: 就是一种为了便于收集数据, 使用简单记号填记并予以统计整理, 作进一步分析或作为核对.检查之用而设计的一种表格或图表.2. 查检表的种类:2.1. 记录用(或改善用)检查表主要功用在于根据收集之数据以调查不良项目.不良主因.缺陷分布等情形.通常将数据分类成数个项目, 以符号或数字记录作为分析问题及改善用的图或表.主要功用是为要确认作业实施.机械整备的实施情形或为预防不良事故, 确保安全时使用. 这种点检表可以防止遗漏或疏忽的造成,检查作业基准,机械操作,机械部位等等是否正确. 亦即把非做不可,非检查不可的工作或项目按点检顺序列出,逐一点检并记录之.二. 柏拉图(排列图):1. 柏拉图: 点上累积不良次数(或累积不良率或累积影响度), 并以折线连接这些点则得柏拉图.2. 作柏拉图的步骤:最后,若"其它"项目太大时, 要检讨是否尚有其它重要因素要提出.2.2 将各不良项目不良数及累积不良百分比记入坐标, 用折线连结各累积不良百分比坐标点即得柏拉图. 横轴代表"不良项目", 纵轴左侧代表"不良数或不良百分比", 纵轴右侧代表"累积不良百分比".3. 柏拉图之用途:3.1 作为降低不良的依据;3.2 决定改善的攻击目标;3.3 用于整理报告或记录;3.4 确认或调整特性要因图;3.5 可作不同条件下的评估;3.6 确认改善的效果(改善前后之比较);3.7 应用于发掘现场的重要问题点.4. 哪些数据可以整理为柏拉图:4.1 质量方面:a. 不良品发生数. 损失金额. 可依不良项目别, 发生常所别, 发生制程别, 原料别, 材料别, 机械别,设备别, 作业者别, 作业方法别……等结果或要因区分出情形.b. 消费者的抱怨件数. 修理件数. 抱怨项目别……等.4.2 时间方面------效率a. 作业的效率------制程别或单位作业别.b. 故障率. 修理时间------机械别. 设备别.4.3 成本方面:a. 装配品的零件单价别.b. 商品的原价别.c. 材料或原材料的单价别.4.4 安全方面:火灾的件数------场所别. 职种别及人体部位别.4.5 营业方面:利润的损益------商品销售量别, 销售金额别, 营业所别, 业务员别.三. 特性要因图(因果分析图)1. 何谓特性要因图: 对于结果(特性)与(要因)间或所期望之效果(特性)与对策间的关系, 以箭头连接,详细分析原因或对策的一种图形称为特性要因图. 该图为日本品管权威人士石川馨博士于1952年所发明, 故又称"石川图"; 因其形状似鱼骨, 故亦称鱼骨图; 因其是在阐明原因于结果之关系, 故亦称因果图. 任何现场产品质量发生异常时, 必定有其原因, 所以要解决质量问题时, 必须先找出影响质量特性的原因, 并加以纠正, 使其恢复正常, 则质量自然正常.例: "为何验货速度慢"的特性要因图2. 特性要因图的基本形态2.2 追求对策型 (鱼骨图反转)3. 特性要因图的画法.3.1 决定问题 (或质量)的特性.例如: 不良率. 停机率. 送修率. 抱怨的发生率以及尺寸不良率等.3.2 画特性要因图的骨架., 将特性写在右端, 自左画上一条较粗的干线(称母线)作代表制程, 并在干线的右端画一指向右方的箭头.母线, 此大分枝称为子枝, 较母线略细.大原因可依制程别分类, 一般分为人. 几械. 材料. 方法及其它.3.4 探讨大原因的原因, 再细分为中小原因, 将其记入小骨及枝骨上(称孙枝. 曾孙枝).细分中小原因时, 应注意必须能采取对策者为主要条件, 且有因果关系者归于同一中.小枝骨内.3.5 决定影响问题点之原因的顺序以集中思考自由讨论的方式, 在所列出的原因中认为影响较大的画上红圈, 再从划上红圈中指出认为影响更大者再画上红圈, 一一检讨下去.4. 绘图注意事项4.1 集合全员的知识与经验4.2 应用脑力激汤术, 全员发言4.3 把要因层别4.4 把重点放在解决问题上, 依5W 1H(Who. Where. What. When. Why & How)的方法逐项列出4.5 应按特性别绘出多张特性要因图4.6 原因解析愈细愈好, 但下图没有小骨的鱼骨图是不行的.4.7 确认原因的重要程度, 应考虑其可行性. 价值, 并经讨论表决后决定4.8 应将圈出的重要原因整理出来, 重新制作另一个特性要因图4.9 记入必要的事项于图旁, 例如: 制品名称. 工程名称. 完成日期. 参与者. 上司的确认及特别状况等4.10 质量特性的决定现场以第一线所发生的问题来考虑. 例如:Q (Quality 质量)------ 产品特性. 寿命. 市场抱怨等等C (Cost 成本)------ 工数. 原价等等D (Delivery 交期)------ 生产率. 操作率等等M(Morale 士气)------ 出劝率. 改善提案件数. 团队精神等等S (Safety 安全)------ 整理整顿. 伤害. 安全等等5. 特性要因图的用途5.1 管理用5.2 改善解析用5.3 制定作业标准用5.4 质量管理导入及教育用四. 直方图1. 何谓直方图: 将所收集的测定值或数据之全距分为几个相等的区间横轴, 并将各区间内之测定值或数据所出现的次数累积, 用柱子排起来的图形.2. 直方图的制作:2.1 在全体数据中找出最大值(Max.)与最小值(Min.)2.2 求出全距(Max. - Min.)2.3 决定组数(N): 一般取N=102.4 决定组距h(组距 = 全距 / 组数 = "Max. - Min." / N): 组距最好取"整数"和奇数.2.5 决定各组之上下组界最小一组的下组界 = 最小值 - h/2最小一组的上组界 = 下组界 + 组距依此类推…….2.6 计算各组的组中点("上组界 + 下组界" / 2)2.7 作次数分配表2.8 制作直方图3. 直方图的准则3.1 组距是决定直方图图形的主要因子, 如果组距太大或太小, 图形都会失真.3.2 将数据归成数个组3.3 组数最好大于5而小于153.4 每个组距应该相同4. 直方图的常见形态:正常型偏态型中部为顶峰, 左右两边低且近似对称一些有形位公差等要求的特性值是偏向型分布, 也有的是由于加工习惯造成. 例如由于加工者担心产生不合格品, 在加工孔时常常偏小而呈左偏型, 加工轴时常常偏大而呈右偏型锯齿型双峰型大多由于分组不当或检测数据不准而造成往往是不同材料, 不同设备, 不同操作者生产的两批产品混合在一起高原型测量有误或产生异常的因素而造成主要是由于生产过程中有缓慢变化因素而造成的. 如刀具的磨损, 操作者的疲劳等5. 制程能力分析五.层别法(分层法):1. 何谓层别法: 将不同作业者/作业群体的作业不良率.不同操作设备/原材料对产品的影响率以及不同的操作环境对产品的影响等等用图表的形式层别出来.例如:下图为某缝纫极加工厂, 以同样的缝纫机予A. B. C三名作业员加工时之不良率情形, 取一个星期的不良率(数据见下表), 经比较结果, 发现A作业员之不良率明显地高过B. C作业员, 反映在层别图上表现为A曲线在B. C曲线之上., 应加以检讨.六. 散布图1. 何谓散布图: 为研究两个变量间之相关性, 而收集成对二组数据, 在方格纸上以点来表示出二个特性值之间相关情形的图形.2. 图表的制作2.2 找出数据X. Y之最大值及最小值2.3 画出纵轴与横轴2.4 将各组数据点在坐标上2.5 必要时记入事项YX 3. 散布图之判读3.1 正相关3.1.1 显著正相关: X 增大 Y增大3.1.2 非显著性正相关: X 增大 Y 增大3.2 负相关3.2.1 显著性负相关: X 增大 Y减小3.2.2 非显著性负相关: X 增大 Y减小3.3 无相关3.3.1 X 与 Y 无关系3.3.2 X增大 Y不变3.4 曲线相关: X增大Y随之增大, 但达到某一值后, X增大Y却又减小.4. 散布图的功用4.1 知道两组数据间是否有相关及相关程度4.2 将人员. 机械. 材料. 方法等可能影响原因层别绘制成散布图, 可知何者影响结果4.3 找出相关特性, 依其关系简化检验, 以降低质量成本4.4 两者间呈直线, 可为订立标准之用七. 管制图1. 数据可分为以连续性之计量值(varible value)及以个数计算的间断性之计数值(attribute value)两种.2. 产品之差异主要有三大类:2.1 同体差异(Within-Piece Variation): 指在同一物体上所发生的差异.2.2 异体差异(Piece-to-Piece Variation): 指在同一时间制造的产品差异.2.3 时间性差异(Time-to-Time Variation): 指在不同时间制造的产品差异.3. 构成差异的主要因素有四:3.1 制程(Process): 这因素包括有工具的磨损.机器的震动.设计问题以及水力电力之波动等.3.2 原料(Material).3.3 操作人员(Operator)3.4 其它(Miscellaneous): 这方面包括环境因素如温度.光度以及检查程序等.以上四个因素构成之差异渐趋于稳定及可预测时, 称之为机遇原因差异(Chance cause of variation).机遇原因差异是不可避免的, 其通常都很细小, 而且较难测度. 相反, 有些因素构成的差异会很大及易于测度, 称之为非机遇原因差异(Assignable cause of variation). 假如在生产过程中, 只有机遇原因差异存在, 这生产过程便是在管制状态中, 否则便是不在管制状态中.4. 所谓管制图: 是一种以实际产质量特性与根据过去经验所判明的制程能力的管制界限比较, 而以时间经过用图形表示者. 方法是将指示质量情况的统计指针在图上用点表示出来, 并在图中画出质量管制界线(Control Limits)以作比较. 质量管制图是记录质量演变之时间表, 它显示出生产过程之稳定情况. 如下简图示:5. 计量质量管理图有"X - R管制图". "X - R管制图"及X - Rs管制图三类.5.1 常用的X - R管制图X-Chart Central Line=XUpper Control Limit, UCL for X=X+3s=X+A2RLower Control Limit, LCL for X=X-3s=X-A2RUpper Warning Limit, UCL for X=X+2s=X+(2/3)A2RLower Warning Limit, LCL for X=X-2s=X-(2/3)A2RR-Chart Central Line=RUpper Control Limit, UCL for R=R+3s=D4RLower Control Limit, LCL for R=R-3s=D3RWhere A2,D3 and D4 are factors taken from standard table calculating control chart lines(See att 标准偏差 s=算术平均值的标准偏差 s=例如: 作铁板厚度的 X-R Chart (See attached table B)Central Line=PUpper Control Limit, UCL for P=P+3 P(1-P)/nLower Control Limit, LCL for P=P-3 P(1-P)/nUpper Warning Limit, UCL for P=P+2 P(1-P)/nLower Warning Limit, LCL for P=P-2 P(1-P)/nP-Chart format see attached table C6.2 常用的C管制图Central Line=CUpper Control Limit, UCL for C=C+3 CLower Control Limit, LCL for C=C-3 CUpper Warning Limit, UCL for C=C+2 CLower Warning Limit, LCL for C=C-2 C例如: 布匹斑点不良数的C-Chart, see attached table D.7. 管制图的看法制程是否在管制状态可用下列原则判断:7.1 管制图上的点都出现在管制界线内侧,并没有特别排法时,原则上认为制程是正常.这种状态谓之管制状态;7.2 管制图上有点超出管制界线外时,就判断制程有了异常变化,这种状态谓之非管制状态;7.3 管制图上的点虽然未超出管制界线,但点的出现有下列排法时,就判断有异常原因发生:7.3.1 点在中心线的单侧连续出现7点以上时;7.3.2 出现的点,连续11点中有10点,14点中有12点,17点中有14点,20点中有16点出现在中心线的单侧时;7.3.3 7点连续上升或下降时;7.3.4 出现的点,连续3点中有2点,7点中有3点,10点中有4点出现在管制界线近旁(警界线外)时;7.3.5 出现的点有周期性变动时.8. 管制图的判读8.1 一个正常形态的三项特性如下:8.1.1 管制图上,大多数点子应在中心线附近;8.1.2 管制图上,有少数点子出现在管制界线附近;8.1.3 正常的管制图上没有跑出管制界线的点子.8.2 不正常型态管制图的特性UCL 8.2.1 单独有一个点子出现在3s区域之外者;A区8.2.2 连续三点中有二点落在A区或A区以外者;B区8.2.3 连续五点中有四点落在B区或B区以外者;C区CL8.2.4 连续有八点落在C区或C区以外者.9.制程精密度Cp及其指数Cpk9.1 Cp=(Su-Sl)/6s=(上限规格-下限规格)/6x标准偏差9.2 Cpk=min[(X-LSL)/3S,(USL-X)/3s]=(T-2|M-X|)/6sT=尺寸公差; X=测量值的平均数; M=(标注尺寸最大值+标注尺寸最小值)/2; s=标准偏差.9.3 Cp与Cpk的关系:9.3.1 Cp≧Cpk;9.3.2 Cp只反映数据的集中度(即精密度);9.3.3 Cpk不但反映数据的集中度,而且反映数据的平均值偏离标准中心值的程度(精确度).因差s(See attached table A);21 OF 21。