固体物理课件第二章_晶格热振动 (2)资料

格式：ppt
大小：901.50 KB
文档页数：2

下载文档原格式

固体物理：晶格振动与晶体的热学性质

5. k空间中点的分布密度
k 点在 k 空间中均匀分布，其分布密度为
k
b1 N1
1
b2 N2
b3 N3
N
(2 )3
V
/ (2 )3
简约布里渊区内 k 点的总数等于原胞的数目，即
N
(2 )3
(2 )3
N
相应的简正模式的数目等于体系的自由度数，为
N[(3n 3) 3] 3nN
五、离子晶体中的长光学波
解：原子的平均平方位移为（计及相位因子的任意性）
un2
j
1 2
a
2 j
每个格波的平均能量为
Ej
N
1 2
a2j
1 2
Nm
a2 2
jj
由于 Ej kT ，所以
a
2 j
2kT
Nm
2 j
从而
un2
j
kT
Nm
2 j
四、三维晶格的振动 1. 原子位移的表示方法
第 l 个原胞的位置 R(l) l1a1 l2a2 l3a3
l s
k
动力学方程
ms2 As
s ',
D ,
k
s,
s
'
As
'
该方程共有 3n 个解，其中 3 个为声学模式，其余 3n-3 个为光学模式。
4. K的取值与倒格矢及布里渊区
玻恩-卡门边界条件要求
u(Rl N1a1) u(Rl ) u(Rl N2a2 ) u(Rl ) u(Rl N3a3 ) u(Rl )
I m / 1 2 (M M ') / M
M ' M
当 M’> M 时，就会出现一种所谓的共振模式，这是一种准局域模式，其频率位于原来的频带之中。这种模式虽然不是局域的，但在杂质附近表现的特别强。

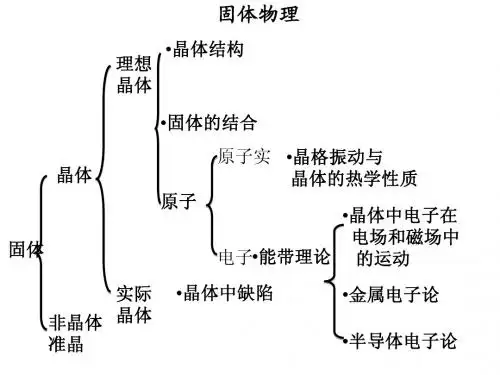
固体物理课件

e 2 晶体中有3N个振动模晶体中有个振动模 C = k ( ∑ B k T ) (eℏω j / kBT − 1)2 V 1）爱因斯坦模型） j =1 B 假设N个原子构成的晶体个原子构成的晶体，假设个原子构成的晶体，
所有的原子以相同的频率 ω0振动 2）德拜模型）以连续介质的弹性波来代表格波，将晶格看作是各向同性的连续介质
V (r + R) = V (r )
布洛赫定理
具有晶格周期性时，布洛赫定理 —— 势场 V ( r ) 具有晶格周期性时，电子的波函数满足薛定谔方程 ℏ2 2 [− ∇ + V ( r )]ψ ( r ) = E ψ ( r ) 2m —— 方程的解具有以下性质
ψ ( r + Rn ) = e ik ⋅R ψ ( r )
ω = 2
−
− i (ωt − naq )
2
β
m
ω
aq sin m 2
−π a
β
π π < q ≤ a a
q=
µn = µn+ N 2π
Na
× h —— h为整数为整数
π a o 晶格振动波矢的数目=晶体的原胞数晶体的原胞数
能量本征值 ε n = ( n q + 1 ) ℏ ω q
q
晶格振动的能量量子；声子 —— 晶格振动的能量量子；或格波的能量量子当这种振动模处于系统能量本征值
原子的振动 —— 晶格振动在晶体中形成了各种模式的波
模型运动方程试探解
m µ n = − β (µ n − µ n−1 ) − β (µ n − µ n+1 )
..
一维晶格振动一维无限长原子链，，，一维无限长原子链，m，a，β

固体物理学_晶格振动与晶体的热学性质之一维单原子链

03_02_一维单原子链 —— 晶格振动与晶体的热学性质
1 能量本征值 nq nq q 2
2 本征态函数 nq (Qq ) q / exp H nq ( ) 2
—— 一个简正坐标对应一个谐振子方程波函数是以简正坐标为宗量的谐振子波函数声子 —— 晶格振动的能量量子；或格波的能量量子当这种振动模处于时，说明有个声子
2 第一布里渊区的线度 a
2 / a N 第一布里渊区状态数 2 / Na
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
—— 格波的色散关系
aq 2 sin( ) m 2
格波相速度 — 不同波长的格波传播速度不同

色散关系
频率是波数的偶函数
03_02_一维单原子链 ——ቤተ መጻሕፍቲ ባይዱ晶格振动与晶体的热学性质
—— 简谐近似下，格波是简谐平面波
—— 格波的波形图向上箭头 —— 代表原子沿X轴向右振动向下箭头 —— 代表原子沿X轴向左振动
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
格波方程格波波长
格波波矢
格波相速度不同原子间相差相邻原子的相差
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
—— 格波的色散关系与连续介质中弹性波的一致
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
格波 —— 短波极限
—— 格波的色散关系与连续介质中弹性波的不一致 —— 不同频率的格波传播速度不同
03_02_一维单原子链 —— 晶格振动与晶体的热学性质
长波极限下
相邻两个原子振动相位差
—— 晶格可看作是连续介质
—— 相邻原子的相位差取值

固体物理各章节知识点详细总结

3.1 一维晶格的振动
3.1.1 一维单原子链的振动
1. 振动方程及其解 (1)模型：一维无限长的单原子链，原子间距(晶格常量)为
a，原子质量为m。
模型运动方程
试探解
色散关系
波矢q范围 B--K条件
波矢q取值
一维无限长原子链，m，a，
n-2 n-1 n mm
n+1 n+2
a
..
m x n x n x n 1 x n x n 1
x M 2 n x 2 n 1 x 2 n 1 2 x 2 n
..
x m 2n1 x 2 n 2 x 2 n 2 x 2 n 1
x
Aei2n1aqt
2 n1
x
Bei2naqt
2n
相隔一个晶格常数2a的同种原子，相位差为2aq。
色散关系
2co as q A M 22B0 m 22A 2co as q B0
a h12 h22 h32
由
2π Kh
d h1h2h3
2π
d K 得： h1h2h3
h1h2h3
简立方：a 1 a i,a 2 aj,a 3 a k ,
b12πa2a3 2πi
Ω
a
b22πa3a1 2πj
Ω
a
b32πa1a2 2πk
Ω
a
b1 2π i a
b2 2π j a
2π b3 k
2n-1
2n
2n+1
2n+2
M
m
质量为M的原子编号为2n-2 、2n、2n+2、···
质量为m的原子编号为2n-1 、2n+1、2n+3、···

第二章3固体物理

之间的体积是图中的球壳的体积。
g() 2
态密度的表达式：
g
V
2 2
2 s3
态密度公式的修正
0
在弹性介质中模或态的密度
上面的讨论已把单个的模与每一个q值联系起来，但对于三维的情形不十分确切。因为对每一个q值，波可以是纵波也可以是横波，实际上与同一个q值相联系，存在三个不同的模式，一种纵的，两种横的。对于纵波和横波，因为它们具有不同的速度，色散关系是不同的。如假设它们存在一共同的速度，态密度关系式修正为：
V 4 q2dq
2 3
在三维空间中传播的波的q允许值（图中
所表示的仅是在qxqy平面中的截面）。阴影部分的圆形壳层是用来计算模数的。
利用色散关系，得到g()d
2
g
d
V
2
3
4
q 2 dq
V
2
3
4
s
d s
这个方程给出了在恒定频率和+d的表面之间的 g ()
点的数目。在q空间中给出的这些表面是球面，它们
• 而对于声学支，0，q0，不管温度多么低，都不能忽略低频对比热的贡献。因只对声学支，可用线性关系，即
q vsq
(6)
且三个方向都相同
• 利用关系式（6），将（4）式的求和改成积分后，
CV T s
vs q d q
e vsq/kBT 1 2 3
(7)
积分范围限在第一布里渊区
• 事实上，在很低的温度下， vsq kBT 部分对（7）式中积分的贡献小到可以忽略，积分可视为在整个q空间中进行。采用球坐标
3N
U E i
i1
3N 1 i1 2
i
e
i

固体物理总结晶格振动与晶体的热学性质完全版

固体物理总结晶格振动与晶体的热学性质完全版第四章总结第四章要求1、掌握⼀维单原⼦链振动的格波解及⾊散关系的求解过程以及格波解的物理意义；2、掌握⼀维双原⼦链振动的⾊散关系的求解过程，清楚声学波与光学波的定义以及它们的物理本质；3、了解三维晶格的振动；4、掌握离⼦晶体长光学波近似的宏观运动⽅程的建⽴过程及系数的确定，清楚LST关系及离⼦晶体的光学性质；5、了解局域振动的概念；6、掌握晶格热容的量⼦理论；熟悉晶格振动模式密度；7、掌握⾮谐效应的概念以及它在热膨胀和热传导中的作⽤。

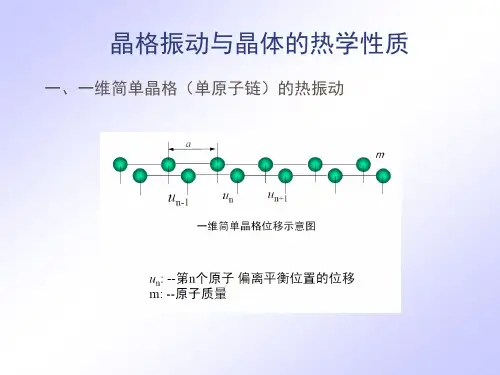
⼀维晶格的振动和三维晶格的振动晶格振动的简谐近似和简正坐标状态及能量确定晶格振动谱的实验⽅法离⼦晶体的长波近似热容晶格振动的爱因斯坦模型热容量德拜模型晶格状态⽅程⾮简谐效应热膨胀1、⼀维单晶格的振动⼀维单原⼦链格波：晶格振动是晶体中诸原⼦（离⼦）集体地在作振动，由于晶体内原⼦间有相互作⽤，存在相互联系，各个原⼦的振动间都存在着固定的位相关系，从⽽形成各种模式的波，即各晶格原⼦在平衡位臵附近作振动时，将以前进波的形式在晶体中传播，这种波称为格波。

相邻原⼦之间的相互作⽤βδδ-≈-=d dv Fa d vd ???? ?=22δβ表明存在于相邻原⼦之间的弹性恢复⼒是正⽐于相对位移的第n 个原⼦的运动⽅程)2(11n n n n m µµµβµ-+=-+?)(naq t i nq Ae-=ωµ⾊散关系：把ω与q 之间的关系称为⾊散关系，也称为振动频谱或振动谱。

)21(sin 4]cos 1[222aq maq mββω=-=其中波数为λπ/2=q ，ω是圆频率，λ是波长有位相差。

相邻原⼦之间的位相差为aq 。

（2）q 的取值范围【－(π/a)""这个范围以外的值，不能提供其它不同的波。

q 的取值及范围常称为布⾥渊区。

前⾯所考虑的运动⽅程实际上只适⽤于⽆穷长的链，⽽两端原⼦的运动⽅程与中间的不同，因此有了玻恩-卡曼提出的环状链模型。

晶格热振动

• 因此可以得到结论： • 可以用独立简谐振子的振动来表述晶体中格
波的独立模式。 • 晶格振动的总能量表述为格波的独立模式能
量之和。
• 根据量子理论，一维简谐振动的能量是量子化的，即频率为ω的振动能量为：
• 三维晶格振动的总能量为：
•能量的量子“ ”称为声子。
ni是频率为ωi的格波模式占据的统计分布：粒子(电子)是不能相互区别的，并且遵守“ Pauli 不相容原理”(原子中不可能有两个或两个以上的电子处于同一量子态)。
f(E) =
表示一个电子占据能量为E的能级的几率
玻色-爱因斯坦统计分布
若考虑到粒子（如光子）虽然相互不能区别,但进入同一能量状态的粒子数不受限制
∙微分形式为： dQ = dE + dA
∙热力学第二定律： dS ≥ dQ/T 对可逆过程取等号，不可逆过程取大于号。
∙系统的自由能F： ∙微分形式为
F = E - TS
dF = -SdT - dA
∙吉布斯函数G： G = F + PV
∙焓H： H = E + PV
∙微分形式为： dG = -SdT - dA + VdP + PdV
1.2材料的热容 1.3材料的热膨胀 1.4材料的热传导 1.5材料的热稳定性
1.1 晶格热振动
1。晶格振动的物理图像
• 晶体内的原子并不是在各自的平衡位置上固定不动的。
• 由于热运动，各原子离开了它们的平衡位置，由于原子间的相互作用，有回到平衡位置的趋势。这两个矛盾相互作用的结果，使每个原子在平衡位置附近作微振动。
•尺寸为 14mmx14mmx14.5mm 的 MC14 （单颗重量8.5g），凭借着铜材质的高导热、以及铸造工艺所造就密集铜柱将显存散热片的散热效能提升到一个新的高度，在官方的演示中，在同样5W热源上和25 度室温环境中，MC14凭借新工艺带来的优势比SKIVING制显存散热片可以多降温6.5度。

(完整版)固体物理课件ppt完全版

布拉伐格子 + 基元 = 晶体结构
③ 格矢量：若在布拉伐格子中取格点为原点，它至其

他格点的矢量 Rl 称为格矢量。可表示为
Rl

l1a1

l2a2

l3a3
，
a1,
a2 ,
a3为
一组基矢
注意事项：
1）一个布拉伐格子基矢的取法不是唯一的
2
4x
·
1
3
二维布拉伐格子几种可能的基矢和原胞取法 2）不同的基矢一般形成不同的布拉伐格子
2·堆积方式：AB AB AB……，上、下两个底面为A
层，中间的三个原子为 B 层
3·原胞：
a, 1
a 2
在密排面内，互成1200角，a3
沿垂直
密排面的方向构成的菱形柱体 → 原胞
B A
六角密排晶格的堆积方式
A
a
B c
六角密排晶格结构的典型单元
a3
a1
a2
六角密排晶格结构的原胞
4·注意: A 层中的原子≠ B 层中的原子 → 复式晶格
bγ a
b a
b a
b a
简六体心底正简单三面心正单方底心单心交立斜交斜方简单立方体心正交面立方简四体心四方简单正交简单菱方简单单斜单方
二、原胞
所有晶格的共同特点 — 具有周期性（平移对称性）
描
用原胞和基矢来描述
述
方
位置坐标描述
式
1、定义：
原胞：一个晶格最小的周期性单元，也称为固体物理学原胞
a1, a2 , a3 为晶格基矢
复式晶格：
l1, l2 , l3 为一组整数
每个原子的位置坐标：r l1a1 l2a2 l3a3

固体物理：6-晶格振动-2

晶格振动2
主要内容
• 声子态密度 • 固体的比热 • 固体的热膨胀 • 局域模 • 离子晶体的长光学波
周期边界条件
态密度为
热力学极限下，k-空间的求和转化为积分
态密度
d 之间，格波数目
g()
V
(2
)3
d
*
3q [
(q)]
求和关系
0
d g ( )
V
(2
)3
d
d
3q
[
(q)]
f
2 x
f
2 y
f
2 z
| fz |
d
3x
[
f
(x,
y,
z)]
S
|
dS f
|
g ( )
V
(2
)3
|
dS
(q)
|
各个维度下的态密度
3D
g ( )
V
(2
)3
|
dS
(q)
|
2D
g ( )
S
(2
)2
dl
| (q) |
1D
g() L
2
(2 ) | d / dq |
态密度的应用
把动量积分转化成频率积分
k
Clq
Ctq
波矢空间的态密度
V
(2 )3
q q dq
状态数量
V
(2
)3
4q 2 dq
V
(2
)3
4q 2 dq
d
q Cl
之间，格波数目
q Ct
1 ( Cl3
2 Ct3
)
V
2
2
2d
g ( )

固体物理学_晶格振动与晶体的热学性质之_晶格振动模式密度剖析

03_09 晶格振动模式密度
晶体中同时可以存在不同频率的简谐振动 —— 不同频率的振动模对应不同的能量
给定晶体 —— 总的振动模数目是一定的按振动频率分布 —— 用晶格振动模式密度来描述
振动模式密度 —— 研究晶体热容、电学和光学性质
晶格振动模式密度 g() lim n —— 单位频范霍夫奇点 —— 晶体中一些高对称点__布里渊区边界 —— 这些临界点与晶体的对称性密切相联
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
ds
(2 )3 q(q)
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
简单几种情况下振动模式密度的表示一维无限长单原子链 —— 最大频率振动模式密度一维情况下
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
考虑到一个频率可以有两个值振动模式密度
g() 2N 1 m2 2
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
q空间 —— 振动模是均匀分布的，状态密度
根据
做出一个等频率面
两个等频率面和
之间的振动模式数目
—— 频率是q的连续函数
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
之间振动模式数目
g() lim n 0
g() V
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
—— 也可以直接由q空间的状态密度来计算状态密度
振动模式密度 g() 2N 1 m2 2
03_09_晶格振动模式密度 —— 晶格振动与晶体的热学性质
德拜近似下的振动模式密度振动频率与波矢成正比
g()
V
2 2c3
2

固体物理复习资料情况总结

第一章晶体结构1、试说明空间点阵和晶体结构的区别。

答：空间点阵是晶体中质点排列的几何学抽象，用以描述和分析晶体结构的周期性和对称性，它是由几何点在三维空间理想的周期性规则排列而成，由于各阵点的周围环境相同，它只能有14种类型。

晶体结构则是晶体中实际质点（原子、离子或分子）的具体排列情况，它们能组成各种类型的排列，因此实际存在的晶体结构是无限的。

当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。

2、证明体心立方格子和面心立方格子互为倒格子证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩rr r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r213422()()4a b i j k i j k a aππ∴=⨯⨯-++=-++r r rr r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r r r r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

所以，面心立方的倒格子是体心立方。

（2）体心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2aa i j kaa i j kaa i j k ⎧=-++⎪⎪⎪=-+⎨⎪⎪=+-⎪⎩rr rrrr rrrr rr由倒格子基矢的定义：1232()b a aπ=⨯Ωr r r3123,,222(),,2222,,222a a aa a a aa a aa a a-Ω=⋅⨯=-=-r r rQ，223,,,,()2222,,222i j ka a a aa a j ka a a⨯=-=+-rr rrrr r213222()()2ab j k j ka aππ∴=⨯⨯+=+r r rr r同理可得：232()2()b i kab i jaππ=+=+r rrr r r即体心立方的倒格子基矢与面心立方的正格基矢相同。

固体物理讲义-第二章(第一和第二节)

弧线为 ω = 2(
β
M
1
) 2 sin
qa ；直线为 ω=Vq。 2
长波极限和短波极限下的原子位移示意图：
q 趋于 0, λ>>a
q 趋于 π/a, λ=2a
两种极限情况下，相邻原子的相对运动情况不同。
(3)格波的相速度(Vp)和群速度(Vg)。两种速度存在不同的物理含义：相速度(Vp)是特定频率为ω，波矢为q的纯波 (单色波)的传播速度；而群速度(Vg)描述平均频率为ω，平均波矢为q的波包(复色
23
《固体物理学》
第二章晶格振动和固体比热
利用欧拉公式： eiθ + e −iθ = 2 cos θ 和 1 − cos θ = 2sin 2
θ
2
ω2 =
2β 4β qa (1 − cos aq ) = sin 2 ( ) M M 2 1 β qa ⇒ ω = 2( ) 2 sin M 2
可以看出上式与n无关，表明n个联立方程都归结为同一个方程。只要ω和q 之间满足上式，就表示上式为联立方程的解。通常把之间的关系称为色散关系。一维单原子链的色散曲线：
X m = Aei ( qma −ωt )
(2)格波波长：
= Aei ( qma + 2π −ωt ) = Aei ( qna −ωt ) = X n ; λ = 2π q
24
《固体物理学》格波与连续介质波的差别：
第二章晶格振动和固体比热
X = Aei ( qx −ωt ) ，式中，连续介质波中 x 表示空间的任一点，而在格波中只
U'= 1 2 β ∑ ( X n − X n +1 ) ， β = u "( a ) ， u ( x ) 表示一维原子链中距离为x的两原子 2 n

固体物理晶格部分复习PPT课件

第3页/共35页
四、晶体的宏观对称性，点群 32个点群，只要求一般了解即可
五、晶系和Bravais格子晶胞：既能反映晶格的周期性又能体现晶体宏观对称
性特征的最小重复单元。注意与原胞的区别
晶胞的坐标系：a ， b ，c
晶胞参量：a，b，c，，，线指数[lmn]和面指数(hkl) 七个晶系：根据晶体的对称性特征分类
空位：
1
10
exp
E1 kBT
间隙原子： 2
20
exp
E2 kBT
三、晶体中原子的扩散
晶体中原子扩散的本质是原子无规的布朗运动
第29页/共35页
1. 扩散的宏观规律
扩散第一定律：扩散第二定律：
j Dn n D2n t
不要求会求解扩散方程
扩散系数与温度的关系：
D T
D0
exp
正比 ❖ 在高温下，T>>D，声子的平均自由程主要取决于声子
与声子间的相互碰撞，声子的平均自由程与T成反比 ❖在低温下， T<<D，声子的平均自由程主要取决于声子
与晶体中的杂质、缺陷及晶体边界等的碰撞
第25页/共35页
本章要求：
❖ 会写出一维（简单晶格或复式晶格）晶体链晶格振动的动力学方程，格波方程，并导出色散关系
子、离子或分子时，外界所做的功
第7页/共35页
体积压缩模量
K
V
dP dV
V0
d 2U
dV
2
V0
体积压缩模量的物理意义：产生单位相对体积压缩所需的外加压强
晶体体积： V N r3 为体积因子，只与结构有关
三、离子晶体的互作用能
U
r
Nq2 40r

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

)2
g(EF
)
g(E)

2
E
5 2
5
g(E)

3
E
1 2
2
E

2 5
C N
EF5/ 2

2
6
(kBT )2
3 2
C N
1
EF2

2 5
C N
5
(EF2

5 2
8
1
(kBT )2 EF2 )
3.5 自由电子比热
二、电子气的比热容
若系统中有N个电子,根据比热容的定义 cV 比热容为:

EF )
(kBT)]1对于能量较高的电子,满足
由冲量定理有：
m
dv

dk

e
dt dt
f

mvE
t
3.6 自由电子气的电导率
二、电子导电的准经典处理
mvE

e
t
即:
vE

et
m

由于电子的漂移运动,电子气系统产生一个沿外场方向的电流 jE
jE

nevE

ne2t
m

ne2t
3.2 自由电子的量子理论
一、周期性边界条件
周期性边界条件：

(r (r

Lx Ly
) )

(r ) (r )

(1) (2)
(r Lz ) (r ) (3)
Lx N1a1 Ly N2a2 Lx N3a3
将周期性边界条件（1）式与金属电子的波动方程联立得：
C(EF0
3
)2
0
2
EF0

(3 2
N C
2
)3

2 2m

3N Vc
2
3
2 (3n 2 )23 2m
g(E)
E O
自由电子的状态密度曲线
E 1 N

EdN
0

1 N

E (E)dE
0
1 N
EF0 0
3
CE 2dE

3 5
E
0 F
3.3费米面与态密度
j AT 2eW kBT
里查逊----杜师曼定律
T为绝对温度;A为常数,不同金属A的值不同.
3.7 金属的电子热发射
用电子气模型来计算热电子发射电流的大小:
在波矢空间中,体积元dk dkxdkydkz中电子态的数目为:
dZ

Vc
4 3
dk x dk y dk z
按费米分布,这些态上的电子数密度为:
这种阻力来源于晶格振动(声子)以及晶格中的缺陷和杂质原子与电子间的相互作用.
对于电子运动阻力的定量分析是复杂的,这里用简单的弛豫时间方法来处理.
3.6 自由电子气的电导率
二、电子导电的准经典处理
电子运动的群速度为：
v d d dE(k)
dk dk dk
当晶体外加电场时,电子被加速, 按牛顿力学有:
N CE 2 f (E)dE 0

2
3
CE 2
3
|0

2 3

C
0
3
E2
f
(E)dE
先求积分I：
I
(
EF
)

g
(
E
)
f (E E
)
dE
0
I0g(EF ) I1g(EF ) I2g(EF )

g(EF
)

2
6
(kBT
)2
g(EF
)
I0

3
bT 3
3
低温下金属总的比热容为:
2
KCl
cV cVe cVc T bT 3
1
变形为:
cV bT 2
T
0
Cu
5
10 15 T 2 K 2
金属总的比热容
3.6 自由电子气的电导率
一、弛豫时间近似
若晶体中的电子是完全自由的,则晶体将没有电阻,在外场作用下电子定向运动的速度越来越大直至无穷,这是与实验不相符的.在实际上,电子在晶体内运动时,要受阻力作用.
第三章金属自由电子理论 Free Electronic Theory of Metals
3.0 引言
一、基本内容
经典电子理论及其局限性量子自由电子理论态密度及费米面金属的接触势差电子比热
二、学习要点
掌握量子理论的提出过程掌握态密度的求法熟练掌握费米面的概念
－绝对零度下的费米能级记为：EF0
f (E)
1
EEF
e kBT 1
a. kBT 0
f (E)
1

陡变
E EF E EF
0 E EF
b. kBT 1
1 E EF
f
(E
)

1 02
E EF E EF
c. kBT 2.5
1 E EF
m

在波矢空间中,当电子气系统达到稳定平衡状态后,每个电子的波矢增加了 k

k

mvE

可见:弛豫时间越大,即阻力越小,则导电能力越强.
3.6 自由电子气的电导率
二、电子导电的准经典处理
kx
kx

kx
ky
无外场
有无外场
电场作用下费米球移动示意图
对导电有贡献仅仅是费米面附近的电子
3.7 金属的电子热发射
f (E)
1
E
e kBT 1
—Fermi- Dirac 分布
其中：为电子的化学势, 一般称绝对零度下的电子化学势为费米面
T=0K时，＝EF
f(E)
E EF : f (E) 0 状态全空
1
EF
E EF : f (E) 1 状态全被占据
E

EF

用电子速度表示波矢和能量:
1
dn
E

1
4
mv2
3
f (E)dkxdkydkz
v

2 p
k
mm
所以
dk x dk y dk z

m
3
dvx
dv
y
dvz
3.7 金属的电子热发射
dn

1 4
3

m
3

exp[(
dvx dv y dvz
mv2 2
－－十分重要
3.3费米面与态密度
四、态密度
3.3费米面与态密度
五、自由电子气体的态密度和费米面
对于自由电子，等能面是球面，由上述分析可得
g(E)

Vc
2 2
(
2m
2
)
3 2
E
1 2
1
CE 2
其中
C

Vc 2 2
(
2m 2
)
3 2

N (E)dE

EF0
CE
1 2
dE
0

2 3
2m

平面波形式的解 :

(r )

eik r
0
其中 r 为电子的位置矢量，k 为波矢量.
2k 2 E
2m
p

k
上面讨论的是无任何限制的自由电子的性质，它的动量具有确定值，速度与波的群速度一致，而坐标不受任何限制，电子在空间各电出现的几率相等.在金属的自由电子论中，电子的势能为零，但它不完全自由，它的位置受金属边界的限制.
六、与费米面相关的一些概念
对于自由电子，费米面为球面. 费米面上的电子的能量称为费米能, 对应的波矢为费米波矢, 对应的电子的速度为费米速度.
2
由
EF0

2 2m

3N Vc
2

3

k
2 F
2m
得绝对零度时的费米波矢为:
由电子动量 kF0 mvF0 得绝对零度时的费米速度矢为:

3.3费米面与态密度
二、费米面的物理意义
费米能级在k空间的等能面－费米面；绝对零度下，金属中电子态被占据和未被占据的能级分界面；费米能级是绝对零度下电子的化学势；自由电子的费米面为球面。
特别提示：
有些教科书、专著或文章中，将任何温度下的电子化学势均称为费米面，此时费米能级是温度的函数，而
• Semiconductor: Resistance decreases with Temperature. • Why? Temp t, n (“free-up” carriers to conduct)
3.2 自由电子的量子理论
一、波函数与能级
薛定谔方程：
2 2 E
eikxLx 1
kx

2
Lx
nx , nx

0,1,2,
同理有：
ky

2
Ly
ny , ny