当前位置：文档之家 › 张量分析-第二讲

张量分析-第二讲

  • 格式：ppt
  • 大小：1.09 MB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

02张量分析

02张量分析

1.矢量场的旋度 令 a aP 是位置矢量P的矢量值函数，于是 aP 的左旋度 curla 定义为
Tik ek x i
divTk
类似地，二阶张量场 T TP 的右散度 d ivT 定义为
T i Tik ik Tik ,i xi
d ivT T
(2.2.19)
ij
a j xi

ai i ai xi
18

显然
a1 a 2 a3 x1 x 2 x3
(2.3.03)
但在T为对称张量的情况下， divT divT ，现证明如下：
divT
diva d iva
因此，今后我们对于矢量场的左散度和右散度不加区别，统一地记为
16
dQ T dQ Q Q dt dt
由式(1.9.10)知
(2.1.11)
dQ dQ T Q Q dt dt
于是
T
T
(2.1.12)
dQ T dQ T dt Q dt Q
所以
2.1
标量的张量值函数的导数
设 T Tt 是标量t(例如时间)的张量值函数。T对t的导数由下式定义：
dTij dT dT 的分量 给出。 由T的分量的导数 dt dt dt ij de 事实上，因为 Tij e i T e j ，又因 i 0 ，故有 dt dTij d ei T e j dt dt dT ei e j dt dT dt ij
(2.2.09)
f i
于是f的微分可写成

f x i
(2.2.04)
df f P dP f P f dx xi i

张量分析第二部分

张量分析第二部分

2.6 张量函数的导数1.张量函数的定义张量函数是指自变量是张量，而函数值是标量、矢量和张量的函数。

例如()B f f =，()ij B f f = (2.6.01)()B a a =，()ijkkB a a = (2.6.02) ()BC C =，()ijk k B C C 11= (2.6.03)分别称作二阶自变量张量B 的标量值、矢量值和二阶张量值的张量函数。

一般说来，这些分量函数的形式在不同坐标系中是不同的，如果它们对所有的单位正交基是相同的，我们就称它们是各向同性张量函数。

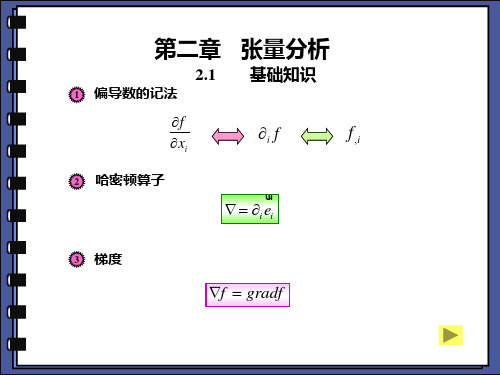
2.张量函数的梯度现在考虑只有一个二阶自变量B 的标量值张量函()B f 数。

B 的增量d B 和f 的微分df 仍然是二阶张量和标量。

这时ij ijdB B fdf ∂∂=(2.6.04) 写成不变性形式，则有B Bd d dfdf :=(2.6.05) 根据商法则可知Bd df也是二阶张量，称之为f 的梯度。

若B 是二阶对称张量，则f 是B 的六个独立分量的函数。

这时在求f 的梯度时，需先在f 里用()ji ijB B+21代替ij B ，求得扩充后的九个偏导数后再按ji ij B B =简化。

例如()()()2211221241B B B f +==B (2.6.06) 于是()1221121221B B B B f =+=∂∂ (2.6.07) 121221B fB B f ∂∂∂∂== (2.6.08) 这一点需要切记，否则如果对()212B f 直接求导，就会导致12212B B f =∂∂的错误结果。

任意二阶张量B 的三个主不变量也是张量函数。

现求它的梯度如下。

由式(1.11.07)—式(1.11.09)知ir ri βδ=1I (2.6.09)js ir rst ijt B B e e 212=I (2.6.10) kt js ir rst ijk B B B e e 613=I (2.6.11)于是mn rn im ri mnrri mn B B B I δδδδ∂∂δ∂∂===11 (2.6.12) ()mnjs ir rst ijt mn B B B e e B I ∂∂∂∂212= (2.6.13) ()()sn jm ir js rn im rj is js ir B B δδδδδδδδ+-=21()[]nm jj mn B B -=δ221()Tmn mn jj B B -=δ (2.6.14)()mnkt js ir rst ijk mn B B B B e e B I ∂∂∂∂613= ()tn km js ir kt js sn jm ir kt js rn im rst ijk B B B B B B B e e δδδδδδ++=61kt js nst mjk B B e e 21=()()()[]kt js js kn ks jn mt jt kn kt jn ms ks jt kt js mn B B δδδδδδδδδδδδδδδ-+---=21()[]mm jj km nk km nt kk nm kt tk kk jj mn B B B B B B B B B B B B -++--=δ21()()()tn T mt T Tmn kk mn kt tk kk jj B B B B B B B B +--=δ21 (2.6.15)把上列三式写成对任何坐标系都适用的不变性形式，则有I B =d dI 1(2.6.16) T I d dI B I B -=12(2.6.17) ()2123T T I I d dI B B I B+-= (2.6.18) 利用式凯莱—哈密顿定理(1.12.09)，我们可将式(2.6.18)写成下列形式：()313I B B-=T d dI (2.6.19)在实际应用中常出现复合函数的情形，这时可以利用链式法则进行运算。

数学张量分析

数学张量分析

divT T
divT T Tkiek ei e j j
ij
Tki x j
ek
Tki xi
ek
iTkiek
一般地，divT di，vT当T为对称张量的时候，两者相等
5 旋度
矢量场的旋度：
左旋度：
r
r
curla a
展开后有：
uur
ur
(ekk )(ai ei )
uur
＝ ekijk ai ej
(i j f )ij
ii f 11 f 22 f 33 f
2 f 2 f 2 f
x2 y2 z2
2.3 物质导数
r 若 f f (t, r(t))
则：Df f f r f f x f y f z
Dt t r t t x t y t z t
f
x
y
z
t (1 f ) t (2 f ) t (3 f ) t
ur ur 原式 (i ei )(a j ej )
ia j ij iai
1a
右散度表示为： diva a
diva a
ei i a je j
ij
a j xi
ai xi
iai
a1 a2 a3 x1 x2 x3
ur
uur
ur
(2a3 3a2 )e1 (3a1 1a3)e2 (1a2 2a1)e3
（ az
-
ay
r ）i （
ax
-
az
r ）j
（
ay
-
ax
r ）k
y z
z x
x y
右旋度：
curla a a j e j ei i
ej

第2章 张量分析(6.8)

第2章 张量分析(6.8)

第2章 张量分析§2.1矢量空间、基、基矢1．线性矢量空间设有n 个矢量,1,2,,i i n =a ，它们构成一个集合R ，其中每个矢量i a 称为R 的一个元素。

如()i j i j +≠a a 唯一地确定R 的另一个元素，及i k a （k 为标量）也给定R 内唯一确定的元素，则称R 为线性（矢量）空间。

R 中的零元素记为O ，且具有i ⋅=O a O .2．空间的维数设i α为m 个标量，若能选取i α，使得10mi ii =α=∑a且i α不合为零，则称此m 个矢量线性相关，否则，称为线性无关。

例1 位于同一平面内的两个矢量1a 和2a （如图）是线性无关的，即11220α+α≠a a 若1α和2α为任意值，且不全为零。

例2 位于同一平面内的三个矢量1a ，2a ，3a 是线性相关的，则恒可找到1α,2α,3α（不全为零）使1122330α+α+α=a a a 如图： 21133''=α+αa a a集合R 内线性无关元素的最大个数称为集合或空间的维数。

设R 的维数为n ，则记为n R ，欧氏空间为3R 。

3．空间的基和基元素n R 中任意n 个线性无关元素的全体称为n R 的一个基。

基的每个元素称为基元素，由于n R 的n 确良基元素是线性无关的。

于是n R 内任一个元素r 可表示成基元素的线性组合。

设(1,2,,)i i n =a 为n R 的任选的基，则有：10ni ii ='α≠∑a，i α'为任意的不全为零的标量但总可选取00≠α及i α不全等于零，使得010ni i i =α=α=∑r a或者2a1a21x2x3xi i x =r e110()nnii i i i i ==α=-=ξα∑∑r a a①i αα,00≠ 不全等于零，所以i ξ不全等于零，且为有限值。

② n R 内有无限个基，但只有一个基是独立的，因为n R 内至少只有n 个元素是线性无关的。

张量分析-第2讲

张量分析-第2讲
张量分析第2讲张量分析张量分析及其应用张量分析pdf张量分析黄克智pdf张量分析视频物理学中的张量分析张量分析简明教程张量分析及其应用pdf弹性力学与张量分析
张量分析 ( Tensor analysis)
华中科技大学力学系 罗俊
版权所有 2011 华中科技大学力学系
1
1.5 坐标变换
已知某物理量或数学物理方程在一个坐标系的表达式, 求它在其它坐标系的相应形式。 旧坐标系 新坐标系
10
3. n阶张量 设物理量T共有3 个分量，且满足坐标变换关系:
n
T
' ' i1 i n
T
' ' i1 in
' i1 j1
' i2 j2
' in j2
j1 j n
则称T为n阶张量。 T
称为n阶张量T的逆变分量。
总共多少种分量? 每种多少个分量? 坐标变换关系如何写? 指标升降关系如何写?
T ab 是二阶张量，将a, b在基矢上分解 :
T ab a i g i b j g j ai g i b j g j a i b j g i g j ai b j g i g j
相应地:
T T g i g Ti g g j T g i g j Tij g g
5
坐标变换系数求法
协变变换 旧---新
j x i 'j i ' x
j' x i j ' i x
逆变变换
i' x ij ' j x
i x ij ' j ' x
互逆
新---旧
4. 矢量分量的坐标变换关系 根据基矢的坐标变换关系可以得到矢量分量的坐标变 换关系:

弹塑性力学课件

弹塑性力学课件
i,j
任晓丹 第二讲：张量分析基础
矩阵的标量函数
aij bij = A : B
张量概述 张量的运算和性质 张量分析初步
矩阵
矩阵的向量函数 y1 = f1 (B) y2 = f2 (B) y3 = f3 (B)
线性函数
∑ 1 y1 = ∑i,j aij bij y2 = i,j a2 bij ∑ ij 3 y3 = i,j aij bij
标量
标量 x, y, x1 , y1 , ...... 标量函数 y = f(x), y1 = g(x1 ), ...... 线性标量函数 (线性变换) f(x1 + x2 ) = f(x1 ) + f(x2 )
线性函数的表示 f(x1 + x2 ) = f(x1 ) + f(x2 ) ⇐⇒ y = ax
张量概述 张量的运算和性质 张量分析初步
Why？
弹塑性力学的三要素：非线性、多维、基础。 张量是适用于多维函数、方程以及微分系统 等的表示工具。 张量的本质是（多维、一般）线性变换。
任晓丹
第二讲：张量分析基础
张量概述 张量的运算和性质 张量分析初步
What？
任晓丹
第二讲：张量分析基础
张量概述 张量的运算和性质 张量分析初步
任晓丹 第二讲：张量分析基础
张量概述 张量的运算和性质 张量分析初步
向量
向量 x = [x1 , x2 , x3 ]T , y = [y1 , y2 , y3 ]T
向量的标量函数 y = f(x) = f(x1 , x2 , x3 )
线性函数 f(x1 + x2 ) = f(x1 ) + f(x2 ) ⇐⇒ y = a1 x1 + a2 x2 + a3 x3 =

张量分析课件-2.2 正则与退化的二阶张量


T
1 1
T
T T
T 1
满射性 对于正则的二阶张量T 对于任意矢量u 所做的线性 变换T· u=w，必存在唯一的逆变换，使T -1· u=w。
i 1 i 1
I
I
定理 三维空间中任意二阶张量T 将任意矢量组u，v，w 映射 为另一矢量组，满足
T u
T v T w detT u v w
证明 （式1.8.25）、(1.8.22)

detT
lmn
u v w detT u v w
l m n

Hale Waihona Puke T uT v T w
ijk
T uT v T w
i l
l
j m m
k n
n
2.2.2 正则与退化
定义 detT≠0的二阶张量T 称为正则的二阶张量；否 则称为退化的二阶张量。 若T 是正则的，则T T 也是正则的。 正则二阶张量的性质： （1）定理 二阶张量是正则的必要且充分条件是将每一组 线性无关的矢量组u(i)(i=1，2，3)映射为另一组线性无关的 矢量组T· u(i)(i=1，2，3)。 等价表述： 二阶张量是正则的必要且充分条件是 T· u=0，当且仅当u=0；或者，二阶张量是退化的必要且 充分条件是存在u≠0 使得T· u=0。 （2）正则的二阶张量T 映射的单射性 对于任意2 个不等 的矢量u≠v，被T 映射以后仍不相等：T· u≠T· v。
（3）正则的二阶张量T 映射的满射性 定义 对于正则的二阶张量T，必存在唯一的正则二 阶张量T -1，使
T T 1 T 1 T G
T -1 称为正则的二阶张量的逆，正则的二阶张量也称为可逆 的二阶张量。可证

第二章张量分析


rT
ij
k
r i
g
j
g
k
rT rj k g j k
若 T a ai )
gr [(rai )gi ai pri g p ]
r
ai
r i
ai
p r ri p
rar
ai
r ri
r ri
i (log
g ) r (log
g)
div a rar arr (log
每项偏导只对其后带点的符号求导
2.10.1协变导数
i p
gr[(rT ij k )gi
gj
gk
T ij k
(
g p ri p
gj
gk
g p rj i
gp
gk
g k rp i
gj
g p )]
j p
k p
g r [(rT ij k ) gi
gj
gk
T ijk (
g i
rp i
gj
gk
g j
rp i
iak
ak ;i
iak
ap
k ip
2.10.2 逆变导数
协变导数的指标是张量指标，故可通过逆 变度量张量升高协变导数的指标来定义逆变 导数如下：
sT ij k g srrT ij k
2.10 不变性微分算子
––– 梯度、散度、旋度、拉普拉斯算子
以三阶混合张量
T T ij k gi g j gk T ij k gij k
若 T a ai gi ，则 curla grr (ai gi ) gr r (ai gi )
gr r ai gi gr gir ai srir ai gs
2.10.4拉普拉斯算子 设 T T ij k gi g j gk 2T T rrT ij k gij k

第二章 张量分析

P也可用另外三个变量 x，1' x，2' 来x 表3' 示，即
P P x1' , x 2' , x 3' P x i'
这种坐标系记为 xi。' 这两组变量
x1 , 和x 2 , x 3 表示x同1' 一, x空2' , x 3'
间点的位置。两者由下列坐标变换联系起来：
xi xi xi'
aigi a jg j aia j gi g j
aiaj 0
令
gij gi g j
g ij g i g j
gi j gi g j g j gi
它们分别称为协变度量张量、逆变度量张量和混合度量张量
考虑到矢量a的任意性 g ji gi g j i j
可知：基矢量 g与i 是g i 正交的，它们称为互逆基矢量 互逆基矢量间具有下列关系：
gig j g k gi g j g k gig j g k eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk
由此定义可知
123 g1g 2g3
123 g1g 2g3
对于矢量 a 0 ，则有
a 2 a a a i g i a j g j a i a j g i g j ai gi a j g j ai a j gi g j
(ii) x 2' (常 数 C)为2 通过z轴的平面； (iii) x3' (常z 数 C)3为垂直于z轴的平面；
和坐标曲线：
(i) x1' 和r C1 x的2' 交线 (zC线2 )是直线； (ii) x 2' 和 C2 的x3'交线z (r线C3)是直线；

北航张量分析课件02


②各项中哑标必须成对出现（不能有两 个以上相同的哑标符号），符号可任换， 各项的展开项数由哑标数决定。
③在指标符号不变的情况下指标式的代 数运算规则与常规代数式运算规则 相同 (这是由代数运算的交换律、结合律、分 配律等代数运算规则所保证的。).
3
指标一致性法则
k x j x j i xi xk x j x j xi xk i
Sij Sij
ij Cijkl kl
1.2 将分量式写为指标式
a11 a21 a 31 a12 a22 a32 a13 x1 b1 a23 x2 b2 x b a33 3 3
1.3 叉积与轴向量 10
置换符号 ijk
1 ijk 1 0
对于右手系
ijk 的偶排列 123 ,231, 312 正循环排列 ijk 的奇排列 132 ,321, 213 逆循环排列 ijk 的重复排列 等价于
1
i, j,k
e j ek ijk ei
由矩阵乘法的行列式性质
ijk e , e , e i j k
eir er eir emr e jr er e jr emr
ek1 ek2 ek3 e em3 en3 eir enr ei e ei em ei en e jr enr e j e e j em e j en ek e ek em ek en
22
1.6利用向量基本特性（见公理化定义） 及叉积基本运算特性:
a b b a
证明：
a b a b
a b c a c b c
a b a b a b a b
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
k j
i k
j j j
3
j j i
j i
i i

i
k j
l k
l i
• 2. 张量相关的概念
P g ( P g1 P g 2 ) g P
1 1 2 1 2 1 2 2
1 2
P g ( P g1 P g 2 ) g P P g1 ( P 1g P 2 g ) g1 P 1
并矢表示法 Tij g g
i
T ij
j ij
T ij T gi g j
Ti j T gi g
i j j
Ti g i g j
j
1.7 张量的代数运算
• 相等
• 相加
同阶张量才可相加
• 数乘
• 并乘
l TS T ij g i g j S k g k gl l T ij S k iu g u '
i
j
ab a1b1g 1 g 1 a1b2g 1 g 2 a1b3g 1 g 3 a2b1g 2 g 1 a2b2g 2 g 2 a2b3g 2 g 31 a3b1g 3 g 1 a3b2g 3 g 2 a3b3g 3 g 3
• 3 张量的解析定义及表示
在坐标系变换时,满足如下变换关系的量称为张量
'


k m'
s' j
g s'

k m'
gm
'

m'
n' l
g n'



u' i
u' i
T
s' j ij s' j

n' l
S g u' g s' g
m'
l k
g n'


k m'
U
n' l
ijl k
gu' g s' g
g n'
U
u ' s ' n ' m '
11 12 13 (n ) 22 23 n t 21 31 32 33
σ
张量
• 1.8 张量矢积
置换符号
eijk e
ijk
1 若i, j , k 1,2,3, 2,3,1, 3,1,2 1 若i, j , k 3,2,1, 2,1,3, 1,3,2 0 若有两个或三个指标相 等
置换符号与克罗尼克尔记号
eijk e ijk
1 若i, j , k 1,2,3, 2,3,1, 3,1,2 1 若i, j , k 3,2,1, 2,1,3, 1,3,2 0 若有两个或三个指标相 等
1 i 0
j
当i j 当i j
1 i 1 2 i 2 3 i 3
i a j a a a ai
j
Amj A A2 j A3 j Aij
m i 1 i 1j 2 i 3 i
3
i
i
1 1
2 2
3 3
i
U
k m'
u' i
s' j
n' l
ijl k
• 缩并
k l S T Tij g g g g kl i j l k Tij kl j gig

i' k '
k Tij g g kj i
Sik g i g k
S T
主讲：黄生洪
中国科学技术大学近代力学系
小结
1 张量相关的一些简化表示方法
指标记法和爱因斯坦求和约定 关于置换符号与克罗尼克尔记号
2 张量相关的概念
协变、逆变基矢量、协变/逆变分量 并矢，基并矢
3 张量的解析定义及表示
1. 张量相关的一些简化表示方法
指标记法和爱因斯坦求和约定
例如, 三维空间任意一点P在任意坐标系
t
(e1 )
(n )
t
(e1 )
n1 t
(e2 )
n2 t
Байду номын сангаас
(e3 )
n3
t 11e1 12e2 13e3 (e2 ) t 21e1 22e2 23e3 n n1e1 n2e2 n3e3 (e3 ) t 31e1 32e2 33e3
T (i , j , k ,...l ) T (i, j , k ,...l )
' ' ' '
i' i
j' j
k' k
l' l
i, j , k ,..l 1,2,...n
m个
m次线性齐 次变换
n维空间m阶张量
张量的阶——自由指标的数目
分量表示法 Tij
x ,x ,x
1 2
3
用指标记法 表示为
x,
i
i 1,2,3
爱因斯坦求和约定
S a1x 1 a2 x 2 an x n
S ai x i a j x
i 1 j 1
约定
n
n
j
求和指
标与所用 的字母无 关
S ai x a j x
i
j
指标重
复只能一 次
31 32 33
A xi y j zk
ijk
代表27项 的和式
自由指标
A11 x 1 A12 x 2 A13 x 3 b1 A21 x 1 A22 x 2 A23 x 3 b2 A31 x 1 A32 x 2 A33 x 3 b3
筒写为
Aij x bi
j
j ——哑指标 i——自由指标，在每一项中只出现一次，一个公式 中必须相同
i' j' k ' j ' i' u

j' s

'
m k'
T
n j'
us mn
降价张量
m k snTus mn i' u i' u
T
m k'
un mn

i' u
m k S u m
'
• 点积
• 转置
• 对称化与反对称化
• 商法则
用于判定某些量的张量性！
1 2
P g2 (P 1g P 2g ) g 2 P 2
1 2
g g gj
i
ij
g i g ij g
j
j
g g g
ij i
g ij g i g j
并矢，基并矢
a ai g , b b j g
i i j
j
ab ai g b j g ai b j g g
置换张量与
等式
可以证明
gi g
j
ijl g l mnl im
n j
gl
mnl (g m g i )(g n g j )g l
mnl (g i g m )(g j g n )g l
j
mnl g m g n g l : g i g
用拉丁字母表示3维，希腊字母表2
维
指标范
围
A xi y j
ij
3
3
双重求和
i 1 j 1
ij
A xi y j A x1 y1 A x1 y2 A x1 y3
11 12 13
A 21 x2 y1 A 22 x2 y2 A 23 x2 y3 A x3 y1 A x3 y2 A x3 y3