圆锥的认识练习培训资料

3.5 圆锥的认识
1．填一填。

（1）圆锥的底面（），侧面展开图（）。

（2）从圆锥的（）到底面（）的距离是圆锥的高。

（3）圆柱的高有（）条，圆锥的高有（）条。

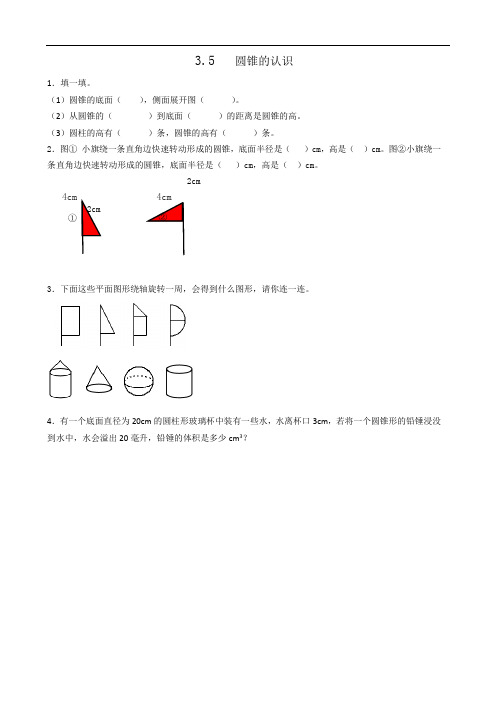
2．图①小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

图②小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

2cm
4cm 4cm
2cm
3．下面这些平面图形绕轴旋转一周，会得到什么图形，请你连一连。

4．有一个底面直径为20cm的圆柱形玻璃杯中装有一些水，水离杯口3cm，若将一个圆锥形的铅锤浸没到水中，水会溢出20毫升，铅锤的体积是多少cm3？
①②
答案:
1．圆扇形顶点圆心无数条一条2．2 4 4 2
3．略
4．14×（20÷2）2×3+20=962cm3。

《圆锥的认识》同步练习一、单选题1、圆锥的高有( )条、A、无数 B。

3 Ｃ。

1【答案】C【解析】【解答】依照圆锥的高的定义可知:圆锥只有一条高;【分析】紧扣圆锥的特征:从圆锥的顶点到底面圆心的距离是圆锥的高;即可解决问题。

故选:C2、圆柱与圆锥的侧面都是( )A、平面B、曲面Ｃ、长方形【答案】Ｂ【解析】【解答】圆柱与圆锥的侧面都是曲面;ﻫ【分析】依照圆柱与圆锥的特征:圆柱与圆锥的侧面都是曲面;进行选择即可。

ﻫ故选:B3、圆锥的侧面展开后是一个( )A、圆Ｂ、扇形 C、三角形 D。

梯形【答案】B【解析】【解答】依照圆锥的特征可知:圆锥的侧面展开后是一个扇形;【分析】依照圆锥的特征:圆锥的侧面展开后是一个扇形,据此选择即可。

故选:B4、圆锥的底面半径一定,体积与高( )A。

成正比例Ｂ。

成反比例 C、不成比例【答案】Ａ【解析】【解答】因为,底面半径一定,因此这圆锥的底面积就一定,ﻫV＝sh ,因此,V÷h= s(一定),ﻫ即圆锥的体积与高的比值一定,ﻫ因此,圆锥的体积与高成正比例;【分析】径确定圆的大小,因为底面半径一定,因此这圆锥的底面积就一定,依照圆锥的体积公式明白,圆锥的体积=×底面积×高,得出圆锥的体积÷高＝底面积,而底面积一定, 是常数,因此圆锥的体积与高的比值一定,因此圆柱的体积与圆柱的高成正比例。

故选:Ａ5、有一条高的立体图形( )A。

圆柱Ｂ、长方体 C、圆锥【答案】C【解析】【解答】A,圆柱有无数条高,即不符合;B,长方体有4条高,不符合题意;ﻫC,圆锥只有一条高,符合条件;【分析】要选出有一条高的立体图形是哪种图形,要对给出的答案进行依次解析,进而得出答案。

ﻫ故选:C６、把这面小旗旋转后得到的图形是( )Ａ、长方形 B、圆柱 C、圆锥 D。

球【答案】B【解析】【解答】解:如图:ﻫ小旗旋转是以小旗的旗杆(小棒)为旋转轴,快速旋转,得到的是一个圆柱;ﻫ【分析】点动成线,线动成面,面动成体、由于长方形或正方形的对边相等,长方形或正方形以它的一边为轴旋转一周就成为一个圆柱,一个直角梯形绕直角腰旋转得到一个圆台,一个直角三角形绕直角边旋转得到一个圆锥、故选:Ｂ7、圆锥的高一定,底面积与体积( )A、不成比例B、成正比例 C。

《圆锥的认识》练习（2）
1、口算
3.14×2= 3.14×3= 3.14×4= 3.14×5= 3.14×6=
3.14×7= 3.14×8= 3.14×9= 3.14×10= 3.14×0.1=
2.填空。

（1）圆锥的底面是个（），从圆锥的顶点到底面圆心的距离是圆锥的（），圆锥有（）条高,圆锥的侧面是一个曲面，侧面展开图是一个（）形。

（3）将下图中的直角三角形以长6cm的直角边所在直线为轴旋转一周，可以得到一个（），这个图形的高是（）cm，底面直径是（）cm。

以长5cm的直角边所在直线为轴旋转一周，可以得到一个（），这个图形的高是（）cm，底面直径是（）m。

2.如下图，在等腰三角形ABC中，AD＝6dm，BC＝8dm，以AD所在直线为轴旋转半周。

（1）可以得到一个什么立体图形？
（2）这个立体图形的底面积是多少？高是多少？。

圆锥的认识练习
知识点一圆锥各部分的名称及特征
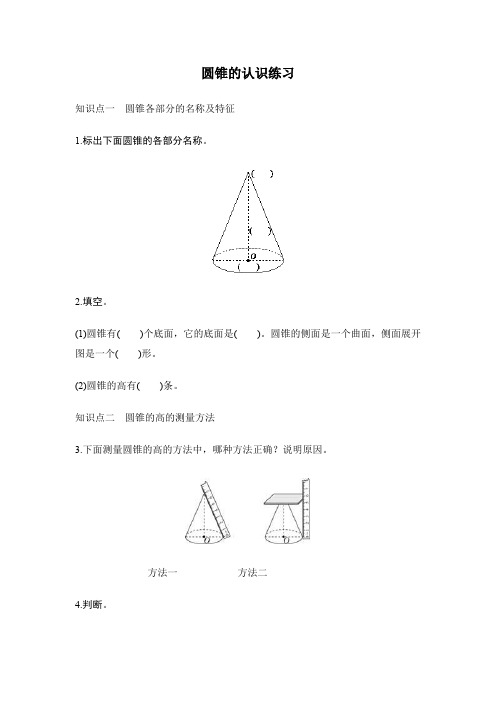
1.标出下面圆锥的各部分名称。

2.填空。

(1)圆锥有()个底面，它的底面是()。

圆锥的侧面是一个曲面，侧面展开图是一个()形。

(2)圆锥的高有()条。

知识点二圆锥的高的测量方法
3.下面测量圆锥的高的方法中，哪种方法正确？说明原因。

方法一方法二
4.判断。

(1)从圆锥的顶点到底面圆周的距离是圆锥的高。

()
(2)圆锥的侧面展开后可能是一个长方形。

()
(3)以一个直角三角形的任意一条边所在的直线为轴旋转一周，都可以得到一个圆锥。

()
(4)圆柱的高有无数条，所以圆锥的高也有无数条。

()
5.下面各图形绕轴旋转一周后得到的分别是哪个图形？连一连。

6.如下图，在直角三角形ABC中，AB＝6 dm，BC＝4 dm，以AB边所在的直线为轴旋转一周。

(1)可以得到一个什么立体图形？
(2)这个立体图形的底面周长是多少？。

小学数学圆锥的认识练习题圆锥是几何学中的一个重要概念，它在小学数学中也扮演着重要的角色。

通过认识和练习圆锥，学生不仅可以提高对几何形体的认识，还可以培养解决问题的能力。

以下是一些关于小学数学圆锥的认识练习题。

第一题：圆锥的定义请简洁明了地解释什么是圆锥？（长度范围：100-150字）第二题：圆锥的特点1. 圆锥的底面是一个圆，顶点在与底面圆中心在一条直线上的点上。

请画出一个示意图来说明这个特点。

（附图，不计入字数）2. 圆锥的侧面是由无数个连接顶点与底面上的点的直线段组成的。

请解释这个特点。

（长度范围：150-200字）第三题：圆锥的种类圆锥可以根据底面和侧面之间的关系分为三种种类，分别是直圆锥、斜圆锥和正圆锥。

请从以下选项中选择正确的说法，并解释其理由。

（长度范围：150-200字）A. 当侧面与底面垂直时，圆锥为直圆锥。

B. 当侧面与底面成锐角时，圆锥为直圆锥。

C. 当侧面与底面成钝角时，圆锥为斜圆锥。

D. 当侧面与底面成锐角时，圆锥为正圆锥。

E. 当侧面与底面成锐角时，圆锥为斜圆锥。

第四题：圆锥的表面积与体积现有一个半径为4厘米、高度为6厘米的圆锥，求其表面积和体积。

（长度范围：200-250字）第五题：圆锥的应用请举例说明圆锥在日常生活中的应用。

（长度范围：150-200字）通过完成以上的认识练习题，相信同学们对于小学数学中的圆锥有了更深入的理解。

希望这些练习题能够帮助大家巩固对圆锥的概念和特点，并能够应用到实际生活中。

人教版六年级数学下册课课练
3.5 圆锥的认识
1．填一填。

（1）圆锥的底面（），侧面展开图（）。

（2）从圆锥的（）到底面（）的距离是圆锥的高。

（3）圆柱的高有（）条，圆锥的高有（）条。

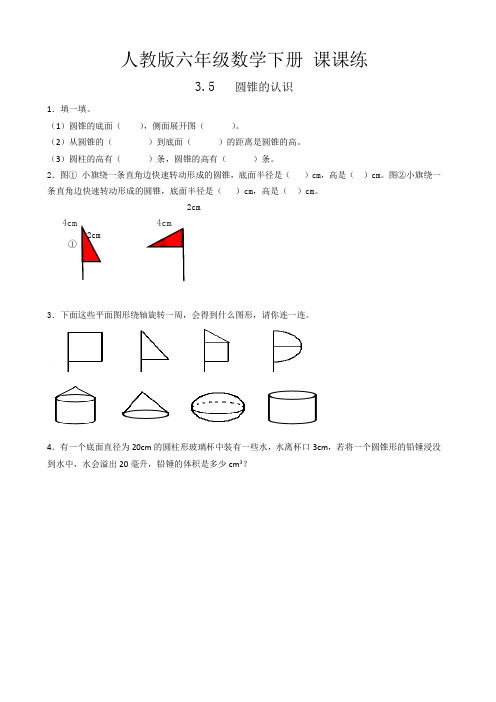
2．图①小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

图②小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

2cm
4cm
4cm 2cm
3．下面这些平面图形绕轴旋转一周，会得到什么图形，请你连一连。

4．有一个底面直径为20cm的圆柱形玻璃杯中装有一些水，水离杯口3cm，若将一个圆锥形的铅锤浸没到水中，水会溢出20毫升，铅锤的体积是多少cm3？
①②
答案:
1．圆扇形顶点圆心无数条一条2．2 4 4 2
3．略
4．14×（20÷2）2×3+20=962cm3。

圆锥与圆锥练习题圆锥与圆锥练习题圆锥是几何学中的一种重要的几何体，它在我们的日常生活中无处不在。

从建筑物的尖顶到冰淇淋的形状，圆锥都存在着。

因此，了解圆锥的性质和应用是非常重要的。

在本文中，我将与大家分享一些有关圆锥的知识，并提供一些练习题供大家练习。

首先，让我们来了解一下圆锥的定义和性质。

圆锥是由一个圆和一个顶点连接而成的几何体。

它有一个平面底面和一个尖顶。

底面上的圆被称为底圆，而连接底圆和尖顶的曲线被称为侧面。

圆锥的侧面是一个斜面，它的形状可以根据底圆的大小和高度的不同而变化。

圆锥的体积和表面积是我们在学习圆锥时经常遇到的概念。

圆锥的体积表示圆锥所占据的空间大小，可以通过以下公式计算：V = 1/3πr²h，其中V表示体积，π表示圆周率，r表示底圆的半径，h表示圆锥的高度。

圆锥的表面积表示圆锥的外部曲面积，可以通过以下公式计算：S = πr² + πrl，其中S表示表面积，l表示圆锥的斜高。

现在，让我们来解决一些关于圆锥的练习题。

这些练习题将帮助我们更好地理解圆锥的性质和应用。

练习题1：一个圆锥的底面半径为8cm，高度为12cm。

计算该圆锥的体积和表面积。

解答：根据上述公式，我们可以计算出该圆锥的体积和表面积。

首先，计算体积：V = 1/3π(8²)(12) = 256π cm³。

然后，计算表面积：S = π(8²) +π(8)(√(8²+12²)) = 256π + 32π√10 cm²。

练习题2：一个圆锥的底面半径为5cm，斜高为13cm。

计算该圆锥的体积和表面积。

解答：根据上述公式，我们可以计算出该圆锥的体积和表面积。

首先，计算体积：V = 1/3π(5²)(√(13²-5²)) = 125π cm³。

然后，计算表面积：S = π(5²) +π(5)(13) =50π + 65π = 115π cm²。

3.5 圆锥的认识
1．填一填。

（1）圆锥的底面（），侧面展开图（）。

（2）从圆锥的（）到底面（）的距离是圆锥的高。

（3）圆柱的高有（）条，圆锥的高有（）条。

2．图①小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

图②小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

2cm
4cm
4cm 2cm
3．下面这些平面图形绕轴旋转一周，会得到什么图形，请你连一连。

4．有一个底面直径为20cm的圆柱形玻璃杯中装有一些水，水离杯口3cm，若将一个圆锥形的铅锤浸没到水中，水会溢出20毫升，铅锤的体积是多少cm3？
①②
答案:
1．圆扇形顶点圆心无数条一条2．2 4 4 2
3．略
4．14×（20÷2）2×3+20=962cm3。

锥体专题训练(经典、全面)
锥体是一种非常重要的几何形体，它广泛应用于物理、数学、
工程等领域。

为了更好地掌握和理解锥体，我们需要进行专题训练。

经典训练
经典训练包括以下内容：
1. 基本概念
首先需要了解锥体的基本概念，包括底面、顶点、母线、母线
角等。

只有掌握了这些概念，才能更好地理解后续内容。

2. 母线长度和斜高的关系
通过推导，我们可以得到母线长度和斜高的关系式，即：$l =
\sqrt{h^2 + r^2}$。

这个关系式在实际问题中应用非常广泛。

3. 旋转体的体积和表面积
锥体是旋转体的一种，我们可以通过旋转体的体积和表面积公式，来求解锥体的体积和表面积。

经典训练主要针对锥体的基础知识，掌握这些基础知识可以为后续内容的研究打下坚实的基础。

全面训练
全面训练包括以下内容：
1. 直角锥
直角锥是最简单的一种锥体，但也是应用最广泛的一种。

需要掌握直角锥的体积、表面积、中心重心坐标等相关知识点。

2. 正锥
正锥的底面是一个正多边形，需要掌握正锥的体积、表面积、中心重心坐标等相关知识点。

3. 圆锥
圆锥的底面是一个圆形，需要掌握圆锥的体积、表面积、中心
重心坐标等相关知识点。

此外，还需要了解圆锥的切截面和旋转体
等一些扩展知识。

全面训练中，我们会更深入地研究和掌握不同种类的锥体，从
而更好地应用于实际问题中。

总之，通过锥体的专题训练，我们可以更好地掌握和理解锥体，为后续数学和物理等领域的学习提供帮助。

3.5 圆锥的认识1．填一填。

（1）圆锥的底面（），侧面展开图（）。

（2）从圆锥的（）到底面（）的距离是圆锥的高。

（3）圆柱的高有（）条，圆锥的高有（）条。

2．图①小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

图②小旗绕一条直角边快速转动形成的圆锥，底面半径是（）cm，高是（）cm。

2cm4cm4cm 2cm3．下面这些平面图形绕轴旋转一周，会得到什么图形，请你连一连。

4．有一个底面直径为20cm的圆柱形玻璃杯中装有一些水，水离杯口3cm，若将一个圆锥形的铅锤浸没到水中，水会溢出20毫升，铅锤的体积是多少cm3？①②答案:1．圆扇形顶点圆心无数条一条2．2 4 4 23．略4．14×（20÷2）2×3+20=962cm31.一个底面直径是6厘米的圆柱形容器里装有8厘米深的水,放入一个铁圆锥(完全浸入水中),水面上升到10厘米。

这个铁圆锥的体积是多少立方厘米?2.一个圆锥形的碎石堆,底面积是25.12平方米,高是3.6米,用这些碎石铺在10米宽的公路上,铺2厘米厚,能铺多长?3. 一个底面直径是12 cm的圆锥形木块,沿高把它分成形状、大小完全相同的两个木块后,表面积比原来增加了120 cm2。

这个圆锥形木块的体积是多少?参考答案：1.3.14×（6÷2）2×（10-8）=56.52立方厘米2.2厘米=0.02米25.12×3.6×÷（10×0.02）=150.72米3.解答:120÷2=60(cm2)圆锥的高:60×2÷12=10(cm)3.14××10×=3.14×36×10×=376.8(cm3)。