高中数学技巧之仿射变换

四、仿射变换在初等几何解题中的应用
例5：求椭圆的面积。 分析：椭圆是一个二次曲线，用初等几何和微积分的知识进行推导 比较繁琐。考虑到圆经过仿射变换对应一个椭圆，所以椭圆也可 以通过一个适当的仿射变换对应成一个圆。
解：在直角坐标系下，椭圆
x y 1 a 2 b2
2
2YΒιβλιοθήκη B’ B A O A’ X
第十五章 仿射变换
目录

仿射变换的定义 仿射变换的性质 仿射变换与初等几何的相关联系 仿射变换在初等几何解题中的应用 结束语
一、仿射变换的定义
定义：如果平面上的一个点变换，把共线的任意 三点变成共线的三点，并且保持三点的单比不 变，称这个点变换为仿射变换。
二、仿射变换的性质
1.仿射变换保持同素性:即仿射变换将点变成点, 直线变成直线. 2.仿射变换保持结合性:即仿射变换保持点与直线 的结合关系. 3.仿射变换将向量变成向量,且保持向量的线性关 系
三、仿射变换与初等几何的相关联系
变换群 几何学
射影群
射影几何
仿射群
仿射几何
正交群
欧式几何
四、仿射变换在初等几何解题中的应用
（一）平行投影 平行投影是仿射变换中最基本、最简单的一类。 因此平行投影变换具有仿射变换中的一切性质， 解这类题的关键是选定平行投影方向，应用平 行线段之比是仿射不变量。
四、仿射变换在初等几何解题中的应用
1 2
1 5
D F A
C
G E B
四、仿射变换在初等几何解题中的应用
（四）仿射变换在椭圆中的应用 例4：证明椭圆的外切三角形的顶点与对边上的 切点连线交于一点。 分析：此题是关于线共点的问题，由于椭圆的一 般性以及三角形的一般性，用初等几何比较难 入手，但可以用仿射几何的方法进行转化，变 成特殊的圆，以及正三角形来加以研究。

详细描述
平移仿射变换涉及将图形在二维平面内沿某一方向进行移动，而不改变图形之 间的相对位置和形状。这种变换通常由一个平移矩阵表示，其中包含平移向量 和单位矩阵。平移向量决定了图形移动的距离和方向。
旋转仿射变换
总结词
旋转仿射变换是围绕某一点旋转图形，同时保持图形之间的相对位置和形状不变。
详细描述
旋转仿射变换涉及将图形围绕某一点进行旋转，同时保持图形之间的相对位置和形状不变。这种变换通常由一个 旋转矩阵表示，其中包含旋转角度和旋转中心点坐标。旋转角度决定了图形旋转的角度，而旋转中心点坐标决定 了旋转的基准点。
缩放仿射变换
总结词
缩放仿射变换是改变图形的大小，同时保持图形之间的相对位置和形状不变。
详细描述
缩放仿射变换涉及将图形的大小进行缩放，同时保持图形之间的相对位置和形状不变。这种变换通常 由一个缩放矩阵表示，其中包含缩放因子和缩放中心点坐标。缩放因子决定了图形缩放的程度，而缩 放中心点坐标决定了缩放的基准点。
03
图像校正
通过仿射变换，可以将倾 斜的图像进行校正，使其 恢复水平或垂直状态。
图像拼接
在图像拼接过程中，可以 使用仿射变换将多张图像 进行对齐，实现无缝拼接。
特征点匹配
通过仿射变换，可以将不 同视角下的图像进行对齐， 便于特征点匹配和计算。
计算机图形学中的仿射变换
3D模型渲染
在3D模型渲染过程中，可以使用 仿射变换对模型进行旋转、缩放 和平移等操作，以实现各种视觉
THANKS.
仿射变换的基本性质
仿射变换不改变图形间的相对 位置和大小关系，即保持平行 性和等比例性。
仿射变换可以分解为一系列基 本变换的组合，如平移、旋转、 缩放等。
仿射变换可以保持直线的性质， 如直线的平行性和垂直性。

解析几何中的仿射与相似变换解析几何是数学中一个重要的分支，研究的是平面和空间中的几何图形，其中涉及到各种各样的变换。

在解析几何中，仿射变换和相似变换是两个常见的变换类型，它们在几何图形的研究和应用中发挥着重要的作用。

一、仿射变换仿射变换是指保持直线平行性和直线上的点的比例关系的变换。

形式上，对于平面上的点P(x, y)，经过仿射变换得到的新点P'(x', y')满足以下关系：x' = a1x + a2y + a3y' = b1x + b2y + b3其中a1、a2、a3、b1、b2、b3是常数，且a1b2 - a2b1 ≠ 0。

对于仿射变换，我们可以将其分解成平移、旋转、缩放和剪切四个基本变换的组合。

具体而言：1. 平移变换：平移变换将点P(x, y)移动到新的位置P'(x', y')，其中新位置与原位置的坐标之差为一个常量向量(v1, v2)。

对于平面上的点P(x, y)，经过平移变换得到的新点P'(x', y')满足以下关系：x' = x + v1y' = y + v22. 旋转变换：旋转变换将点P(x, y)绕一个固定的点O(x0, y0)逆时针旋转θ弧度。

对于平面上的点P(x, y)，经过旋转变换得到的新点P'(x', y')满足以下关系：x' = (x - x0)cosθ - (y - y0)sinθ + x0y' = (x - x0)sinθ + (y - y0)cosθ + y03. 缩放变换：缩放变换将点P(x, y)绕一个固定的点O(x0, y0)按照比例因子k进行缩放。

对于平面上的点P(x, y)，经过缩放变换得到的新点P'(x', y')满足以下关系：x' = k(x - x0) + x0y' = k(y - y0) + y04. 剪切变换：剪切变换通过把点P(x, y)沿着某个方向按照比例因子k进行剪切。

高中数学仿射变换一、引言仿射变换是高中数学中的重要概念之一，它在几何变换和线性代数中有着广泛的应用。

本文将介绍仿射变换的基本概念、性质以及应用，帮助读者更好地理解和掌握这一知识点。

二、基本概念1. 定义：仿射变换是指保持直线平行性质的变换。

简单来说，它是由平移、旋转、缩放和投影四种基本变换组成的变换。

2. 仿射变换的代数表示：设二维平面上有一个点P(x, y)，经过仿射变换后得到点P'(x', y')，则有如下代数表示：x' = a*x + b*y + cy' = d*x + e*y + f其中a、b、c、d、e、f为常数。

三、性质1. 保直线性质：仿射变换保持直线的性质，即直线经过仿射变换后仍然是直线。

例如，一条直线上的三个点经过仿射变换后仍然共线。

2. 保平行性质：仿射变换保持平行线的性质，即平行线经过仿射变换后仍然平行。

例如，两条平行线经过仿射变换后仍然平行。

3. 保比例性质：仿射变换保持线段的比例关系。

例如，一条线段上的两个点经过仿射变换后线段上的其他点的比例关系仍然成立。

四、应用1. 几何变换：仿射变换在几何变换中有着广泛的应用，可以用来描述平面上的旋转、缩放、平移等操作。

例如，我们可以利用仿射变换来实现图片的旋转、缩放和平移。

2. 图像处理：仿射变换在图像处理中也有着重要的应用，可以用来进行图像的扭曲、校正和纠正等操作。

例如，我们可以利用仿射变换来对图像进行透视校正，使得图像中的平行线在处理后仍然保持平行关系。

3. 计算机图形学：仿射变换在计算机图形学中扮演着重要的角色，可以用来进行三维物体的平面投影、旋转和缩放等操作。

例如，我们可以利用仿射变换来实现计算机图形学中的三维模型的投影效果。

五、总结通过本文的介绍，我们了解了高中数学中的仿射变换的基本概念、性质以及应用。

仿射变换作为一种保持直线平行性质的变换，在几何变换、图像处理和计算机图形学等领域都有着广泛的应用。

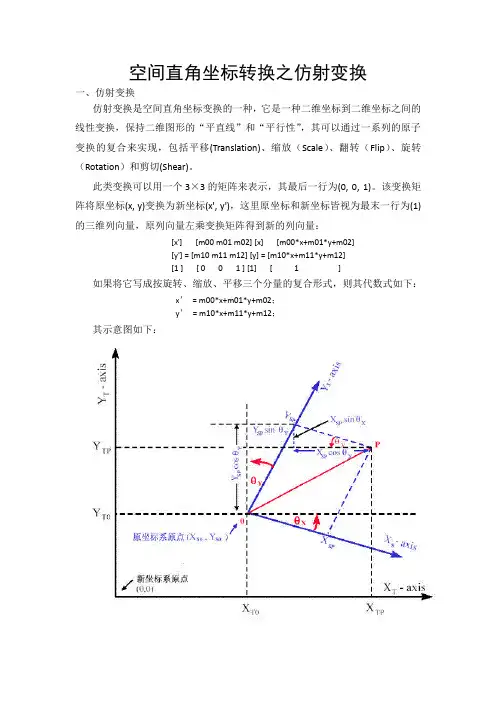
空间直角坐标转换之仿射变换一、仿射变换仿射变换是空间直角坐标变换的一种，它是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直线”和“平行性”，其可以通过一系列的原子变换的复合来实现，包括平移(Translation)、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切(Shear)。

此类变换可以用一个3×3的矩阵来表示，其最后一行为(0, 0, 1)。

该变换矩阵将原坐标(x, y)变换为新坐标(x', y')，这里原坐标和新坐标皆视为最末一行为(1)的三维列向量，原列向量左乘变换矩阵得到新的列向量：[x'] [m00 m01 m02] [x] [m00*x+m01*y+m02][y'] = [m10 m11 m12] [y] = [m10*x+m11*y+m12][1 ] [ 0 0 1 ] [1] [ 1 ]如果将它写成按旋转、缩放、平移三个分量的复合形式，则其代数式如下：x’= m00*x+m01*y+m02；y’= m10*x+m11*y+m12；其示意图如下：几种典型的仿射变换：1.public static AffineTransform getTranslateInstance(double tx, double ty)平移变换，将每一点移动到(x+tx, y+ty)，变换矩阵为：[ 1 0 tx ][ 0 1 ty ][ 0 0 1 ]（译注：平移变换是一种“刚体变换”，rigid-body transformation，中学学过的物理，都知道啥叫“刚体”吧，就是不会产生形变的理想物体，平移当然不会改变二维图形的形状。

同理，下面的“旋转变换”也是刚体变换，而“缩放”、“错切”都是会改变图形形状的。

）2.public static AffineTransform getScaleInstance(double sx, double sy)缩放变换，将每一点的横坐标放大（缩小）至sx倍，纵坐标放大（缩小）至sy倍，变换矩阵为：[ sx 0 0 ][ 0 sy 0 ][ 0 0 1 ]3.public static AffineTransform getShearInstance(double shx, double shy)剪切变换，变换矩阵为：[ 1 shx 0 ][ shy 1 0 ][ 0 0 1 ]相当于一个横向剪切与一个纵向剪切的复合[ 1 0 0 ][ 1 shx 0 ][ shy 1 0 ][ 0 1 0 ][ 0 0 1 ][ 0 0 1 ]（译注：“剪切变换”又称“错切变换”，指的是类似于四边形不稳定性那种性质，街边小商店那种铁拉门都见过吧？想象一下上面铁条构成的菱形拉动的过程，那就是“错切”的过程。

仿射变换例子（实用版）目录1.引言2.仿射变换的定义和基本概念3.仿射变换的例子4.仿射变换的性质和应用5.总结正文1.引言在数学中，仿射变换是一种在向量空间中进行的变换，它可以保持向量的线性关系，即保持向量的平行四边形形状不变。

仿射变换广泛应用于各种学科领域，如物理学、工程学、计算机图形学等。

本文将通过一些例子来介绍仿射变换的性质和应用。

2.仿射变换的定义和基本概念仿射变换是指在向量空间中，将一个点或者一个向量变换为另一个点或向量的过程。

仿射变换保持向量的线性关系，即保持向量的平行四边形形状不变。

仿射变换可以用矩阵来表示，这个矩阵称为仿射矩阵。

3.仿射变换的例子假设有一个平面直角坐标系，原点为 O(0, 0)，点 A(1, 0)，点 B(0, 1)，点 C(2, 1)。

现在我们考虑将这个坐标系进行仿射变换，变换后的坐标系中原点为 O"(a, b)，点 A"的坐标为 (x, y)。

根据仿射变换的定义，可以列出以下方程组：(x - a, y - b) = m(1 - a, 0 - b)(0 - a, 0 - b) = n(0 - a, 1 - b)(2 - a, 1 - b) = p(2 - a, 1 - b)其中，m、n、p 分别为仿射矩阵的三个元素。

解这个方程组，可以得到变换后的点 A"的坐标。

4.仿射变换的性质和应用仿射变换具有以下性质：1) 仿射变换保持向量的线性关系，即保持向量的平行四边形形状不变。

2) 仿射变换具有平滑性，即经过连续的仿射变换，可以得到任意的变换结果。

3) 仿射变换可以用矩阵表示，从而可以利用矩阵的运算法则进行计算。

仿射变换在实际应用中有很多，如在计算机图形学中，仿射变换可以用来实现图形的平移、旋转、缩放等操作；在物理学中，仿射变换可以用来描述物体在空间中的运动等。

5.总结仿射变换是一种在向量空间中进行的变换，它可以保持向量的线性关系，即保持向量的平行四边形形状不变。

下旳像依次为A', B', C'. 若A, B, C共线且B在A, C之间, 则有|AB|+|BC|=|AC|. 由正交变
换旳定义有
| AB | | BC || AC | | A' B ' | | B 'C ' || A'C ' | .
即A', B', C'依然为共线三点且B'在A', C'之间. 若A, B, C不共线, 则必有
定理 仿射变换是双射.设A表达平面上全体仿射变换旳集合. 则有
(1) , A, 有A.
(2) 恒同变换iA.
(3) S, 存在1A, 满足11i.
上述性质使得A对于变换旳乘法构成一种群, 叫做仿射变换群. 而 且MSA.
仿射变换
3. 仿射坐标系
定义 设在平面上取定一点O和以O为起点旳两个线性无关向
量ex, ey, 则由此构成平面上一种仿射坐标系(或仿射坐标架), 记作 O-exey. 平面上任一点P旳仿射坐标(x, y)由下式唯一拟定,
x
OPx OEx
(Px ExO)
y
OPy OEy
(Py EyO)
OP xex yey.
反之, 对任意给定旳有序实数偶(x, y), 由 (1.12)式可唯一拟定仿射平面上旳一种点 具有坐标(x, y). 建立了仿射坐标系旳平面 称为仿射平面, ex, ey称为基向量.
(1.10)
则称为上旳一种以k为相同比旳相同变换.
注. 相同变换旳基本性质 (1) 保持共线三点旳简朴比不变. (2) 使得任意图形变成其相同图形; 使平 行直线变为平行直线. (3) 保持任意两条线段旳比值不变. 从而 保持两直线夹角不变. (4) 正交变换、位似变换都是其特例.

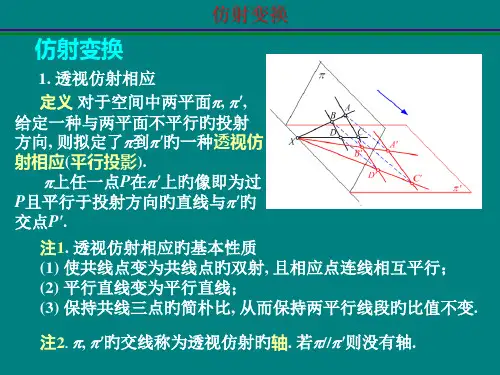
仿射变换和等距变换一、仿射变换1. 概念仿射变换是指在几何空间中，保持直线的平行性和比例关系的变换。

它可以由线性变换和平移变换组合而成，具有保持平行性、保持比例、保持共线性等性质。

2. 性质仿射变换具有以下性质：（1）保持直线的平行性：在仿射变换中，任意两个平行直线经过变换后仍然保持平行。

（2）保持比例关系：在仿射变换中，直线上的任意两点与其对应点的连线与直线上其他点与其对应点的连线的比值保持不变。

（3）保持共线性：在仿射变换中，直线上的任意三点经过变换后仍然共线。

3. 应用仿射变换在计算机图形学、计算机视觉、图像处理等领域有广泛应用。

例如，在图像处理中，可以利用仿射变换对图像进行旋转、平移、缩放和剪切等操作，实现图像的变形、校正和配准等功能。

二、等距变换1. 概念等距变换是指在几何空间中，保持距离不变的变换。

它可以由旋转变换、平移变换和翻转变换组合而成，具有保持距离、保持角度、保持面积等性质。

2. 性质等距变换具有以下性质：（1）保持距离不变：在等距变换中，任意两点之间的距离经过变换后仍然保持不变。

（2）保持角度不变：在等距变换中，任意两线段之间的夹角经过变换后仍然保持不变。

（3）保持面积不变：在等距变换中，平行四边形的面积经过变换后仍然保持不变。

3. 应用等距变换在几何学、物理学、计算机图形学等领域有重要应用。

例如，在地图投影中，可以利用等距变换将地球表面上的经纬度坐标转换为平面上的坐标，实现地图的绘制和测量。

此外，在计算机图形学中，等距变换常用于三维模型的变换和变形，实现真实感的渲染和动画效果。

仿射变换和等距变换是两种常见的几何变换方法。

它们分别具有保持直线的平行性和比例关系、保持距离的性质，并在不同领域中得到广泛应用。

了解和掌握这些变换的概念、性质以及应用，对于理解几何学和计算机图形学的基本原理和方法具有重要意义。

在实际应用中，可以根据具体需求选择合适的变换方法，实现几何形状的变换、校正和配准等功能，提高图像处理和计算机模拟的效果。

仿射变换原理仿射变换是一种将图像进行几何变换的方法，它可以在不改变图像形状的情况下对其进行平移、旋转、缩放和倾斜等变换。

仿射变换的原理是通过对图像进行线性变换和平移变换来实现图像的变换。

线性变换是指将图像中的每一个像素点都进行一定的数学运算，从而对图像进行变换。

常见的线性变换有平移、旋转、缩放和剪切等。

平移变换是指将图像沿着某一方向平移一定的距离，旋转变换是指将图像绕着某一点旋转一定的角度，缩放变换是指将图像按比例缩小或放大，剪切变换是指将图像进行斜切变换。

平移变换可以通过对图像的坐标进行平移来实现。

例如，将图像沿着x轴平移dx个单位，y轴平移dy个单位，可以通过对每一个像素点的坐标进行修改来实现。

具体地，对于一个坐标为(x, y)的像素点，进行平移变换后的坐标为(x+dx, y+dy)。

旋转变换可以通过对图像的坐标进行旋转来实现。

例如，将图像绕着某一点(x0, y0)旋转θ度，可以通过先将图像沿着(x0, y0)平移，然后对每一个像素点的坐标进行旋转，最后再将图像沿着(-x0, -y0)平移回原来的位置来实现。

具体地，对于一个坐标为(x, y)的像素点，进行旋转变换后的坐标为：x' = (x - x0)cosθ - (y - y0)sinθ + x0y' = (x - x0)sinθ + (y - y0)cosθ + y0缩放变换可以通过对图像的坐标进行缩放来实现。

例如，将图像按照x轴和y轴分别缩放sx和sy倍，可以通过对每一个像素点的坐标进行修改来实现。

具体地，对于一个坐标为(x, y)的像素点，进行缩放变换后的坐标为(sx*x, sy*y)。

剪切变换可以通过对图像的坐标进行剪切来实现。

例如，将图像在x轴和y轴方向上分别剪切tx和ty个单位，可以通过对每一个像素点的坐标进行修改来实现。

具体地，对于一个坐标为(x, y)的像素点，进行剪切变换后的坐标为(x+tx*y, y+ty*x)。

大招7仿射变换 大招总结仿射变换,通俗来讲,就是将一个空间内的图形按照一定法则变换,就会在另一个空间内得到与之对应的新图形.在高考数学解析几何题目中,我们可以利用仿射变换将一部分有关椭圆的问题转化为圆的问题,这样就可以借助圆中的特有的一些性质解决问题,从而使问题的解决过程大大简化.椭圆22221(0)x y a b a b +=>>,经过仿射变换x xa y yb '=⎧⎪⎨'=⎪⎩,则椭圆变为了圆222x y a ''+=,并且变换过程有如下对应关系：(1)点()00,P x y 变为00,a P x y b ⎛⎫' ⎪⎝⎭(2)直线斜率k 变为ak k b '=(3)图形面积S 变为aS S b''=(4)点、线、面位置不变(中点依然是中点,相切依然是相切)(5)弦长关系满足||A B AB ''=因此同一条直线上线段比值不变. 仿射变换一般而言主要应用于选填中快速得出结果,对于大题可以利用仿射变换快速得出结果但是容易丟掉步骤分,因此还是用正常方法写出过程.当出现以下几个场景的时候就可以联想仿射变换去处理:(1)面积问题(尤其是有一个顶点是坐标原点的时候);(2)斜率之积出现22b a-之类;(3)同一条线段的比例问题;(4)其他与之相关联的问题.典型例题例1.(2014-新课标)I 已知点(0,2)A -,椭圆2222:1(0)x y E a b a b+=>>的离心率为2F 是椭圆的右焦点,直线AFO 为坐标原点.+ (I)求E 的方程;(II)设过点A 的直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程. 分析:这里第二问出现OPQ ∆面积最大,因此可以联想仿射变换化椭为圆去做..解(I)设(,0)F c ,由条件知2c =得c =,又2c a =,所以2222,1a b a c ==-=,故E 的方程2214x y +=.(II)方法1:依题意当l x ⊥轴不合题意,故设直线:2l y kx =-,设()()1122,,,P x y Q x y 将2y kx =-代入2214x y +=,得()221416120k x kx +-+=,当()216430k ∆=->,即234k >时,21,22824314k k x k ±-=+ 从而2221224143||114k k PQ k x x k+⋅-=+-=+ 又点O 到直线PQ 的距离221d k =+,所以OPQ ∆的面积221443||214OPQk S d PQ k∆-==+,设243k t -=,则2440,144OPQt t S t t t∆>==++,当且仅当72,2t k ==±等号成立,且满足0∆>, 所以当OPQ ∆的面积最大时,l 的方程为:722y x =-或722y x =--. 方法2:作变换2x xy y'=⎧⎨'=⎩,椭圆E 变为圆:224x y ''+=,,此时P Q ''过点(0,4)A '-,此时,2OPQ OPQ S S ∆'∆+=因此OPQ S ∆最大时,OP Q S ∆''同样最大.1sin 2sin 22OP Q S OP OQ P OQ P OQ ∆''='⋅'∠''=∠''当且仅当2P OQ π∠''=时最大 设直线P Q ''方程为4y k x '=''-,那么O 到直线P Q ''距离2421d k '==+17722PQ k k k ⇒'=±⇒='=± ∴直线l 的方程为722y x =±- 总结思考:当过椭圆外一个定点P 作一条直线与椭圆交于,A B 两点时,AOB ∆面积最大值2ab,当且仅当经过仿射变换之后的A B ''与原点O 所构成的三角形为直角三角形时取到最大值.如果定点P 是圆内点,则有两种情况:(1)如果作仿射变换之后P '到圆心距离大于等于22a ,那么面积最大值仍然是;(2)2ab如果作仿射变换之后P '到圆心距离小于22a ,那么当OP A B '⊥''时面积取到最大值.例2.设1F 、2F 分别是椭圆2214x y +=的左、右焦点.(1)若P 是该椭圆上的一个动点,求12PF PF ⋅的取值范围;(2)设(2,0),(0,1)A B 是它的两个顶点,直线(0)y kx k =>与AB 相交于点D ,与椭圆相交于E 、F 两点.求四边形AEBF 面积的最大值. 解(1)由题意可知2,1a b ==,∵c ==∴12(F F 设 (,)P x y∴2212(,),)3,PF PF x y x y x y ⋅=-⋅=+-+()2221133844x x x =+--=-由椭圆的性质可知,2228384x x -⇒--*()212138[2,1]4PF PF x ∴⋅=-∈- (2)方法1:设()()1122,,,E x kx F x kx ,联立2214y kx x y =⎧⎪⎨+=⎪⎩消去y 整理可得()22144k x+=12x x ∴==(2,0),(0,1)A B∴直线AB 的方程为:220x y +-=根据点到直线的距离公式可知,点,E F 到直线AB 的距离分别为1212k h ++==2212k h +==∴12h h+=∴||AB ==∴四边形的面积为()1211||22S AB h h =+===4212214k k=++(当且仅当14k k =即12k =时,上式取等号,所以S 的最大值为22. 方法2:作变换2x xy y'=⎧⎨'=⎩之后椭圆变为圆,方程为224x y ''+=+此时(0,2),22,4B A B E F '''=''=当且仅当E F A B ''⊥''时面积取到最大此时1222ABBF AE B F S S '''==四边形四边形例 3.(2017-肇庆三模)已知圆221:(1)16F x y ++=,定点2(1,0),F A 是圆1F 上的一动点,线段24F A的垂直平分线交半径1F A 于P 点.(I)求P 点的轨迹C 的方程;(II)四边形EFGH 的四个顶点都在曲线C 上,且对角线,EG FH过原点O ,若34BG FH k k ⋅=-,求证:四边形EFGH 的面积为定值,并求出此定值.解(1)解:因为P 在线段2F A 的中垂线上,所以2||PF PA =. 所以211112||4PF PF PA PF AF F F +=+==>所以轨迹C 是以12,F F 为焦点的椭圆,且1,2c a ==,所以3b =。

仿射变换公式仿射变换公式是数学中一种常见的变换公式，使用它可以对一个坐标系中的原点进行变换，从而将它转化为另一个坐标系下的点。

它有助于解决不同的图形学问题、实现图形的转换，也可以用于将两个不同的坐标系之间的数据进行转换。

仿射变换公式的定义如下：设A、B、C是三个二维空间的仿射变换，那么ABC的变换公式为：XA=XB+XC，YA=YB+YC。

其中XA、YA是原坐标系中点P的横纵坐标，XB、YB是原坐标系中点P’的横纵坐标，XC、YC是新坐标系中点P’的横纵坐标（新坐标系相对于原坐标系的平移量）。

仿射变换公式的另一种表示形式为：XA=AXB+BYC，YA=CXB+DYC。

其中XA、YA是原坐标系中点P的横纵坐标，XB、YB是原坐标系中点P’的横纵坐标，XC、YC是新坐标系中点P’的横纵坐标（新坐标系相对于原坐标系的平移量），A、B、C、D是四个不同的仿射变换系数。

仿射变换公式可以用来实现一些基本的图形变换，例如平移、旋转、缩放、拉伸及剪切等。

它也可以用于将两个不同的坐标系之间的数据进行转换，以统一处理某个问题。

例如，在机器视觉中，经常需要将输入的图像从一个坐标系转换到另一个坐标系中进行处理，这就要求把原始图像仿射变换到目标坐标系中。

此外，仿射变换公式还可以用于自然图像的空间变换或是像素点之间的坐标变换。

仿射变换公式的应用非常广泛，它极大地方便了图形学领域中的许多应用，也提供了图形学问题求解的一种重要方法。

例如，多层次变换（MLT）是一种常用的图形学变换技术，它可以用仿射变换公式表示为：XMLT=XL+TR，YMLT=YL+TR，其中XL、YL是原始图像的坐标，TR是与仿射变换相关的参数，XMLT、YMLT是MLT变换后的结果。

仿射变换是一种有效的图形变换手段，它的应用范围很广，在图形学、机器人控制、图像处理等领域都有重要的应用。

它可以用来实现两个不同坐标系之间的数据转换，也可以用于像素点之间的坐标变换，是一种非常重要的变换公式，也是图形学问题求解中不可或缺的工具。

仿射变换的原理和应用1. 什么是仿射变换？仿射变换是一个基本的几何变换，它保持了直线的平行性，并保持了直线上的点的比例关系。

简单来说，仿射变换是将原始图像的点映射到新的位置，同时保持了原始图像上点之间的平行性、直线性和相对位置关系。

仿射变换包括了平移、旋转、缩放、反射和错切等操作。

2. 仿射变换的原理仿射变换的原理基于线性代数和矩阵运算。

对于2D图像，仿射变换可以用一个2x3的矩阵来表示。

假设原始图像上的点为P = (x, y)，经过仿射变换后的点为P’ = (x’, y’)，那么可以通过以下公式计算P’的坐标：[x', y'] = [[a, b, tx], [c, d, ty]] * [x, y, 1]其中，a、b、c、d分别为缩放和旋转参数，tx和ty为平移参数。

对于3D图像，仿射变换可以用一个3x4的矩阵来表示。

3. 仿射变换的应用3.1 图像处理仿射变换在图像处理中有广泛的应用。

通过对图像进行平移、旋转、缩放、镜像等操作，可以实现图像的纠正、修复、变形和增强等功能。

例如，将一个倾斜的图像进行仿射变换，可以使其恢复到正常状态；通过对图像进行缩放、旋转和平移等操作，可以实现图像的放大、旋转和移动。

3.2 计算机视觉仿射变换在计算机视觉领域也有广泛的应用。

例如，通过对图像进行仿射变换，可以实现人脸识别中的人脸对齐；通过对图像进行旋转和平移等操作，可以实现目标跟踪中的目标定位和位置估计。

3.3 计算机图形学仿射变换在计算机图形学中也是一项重要的技术。

通过对图形进行仿射变换，可以实现图形的变形、平滑和动画效果等。

例如，通过对2D图形进行仿射变换，可以实现图形的旋转、缩放和平移等效果；通过对3D模型进行仿射变换，可以实现物体的变形和动画效果。

4. 仿射变换的优缺点4.1 优点仿射变换是一种简单而强大的几何变换方法。

它可以保持图像的直线性、平行性和相对位置关系，同时可以灵活地对图像进行变形、修复和增强。

第2章 仿射变换2．1 平行射影 知识点解析平行射影：对应点之间的连线互相平行．平行射影与方向有关，方向变了，就得出了另外的透视仿射． 仿射对应：有限次平行射影的复合就是一个仿射对应． 仿射变换：平面π到自身的仿射对应，称为仿射变换．平行射影把点映成点，把直线映成直线，这叫做平行射影的保持同素性． 点与线的结合性质在平行射影下保持不变．仿射对应也保持同素性与结合性．即，仿射对应把点映成点，把直线映成直线．若A 在a 上，则A '在a '上．注意：仿射对应不一定是平行射影，即，原象点与象点之间的连线不一定平行，反过来，平行射影一定是仿射对应．解题指导 练习２－１１． 试举例说明在一般仿射对应下，二直线上的对应点的连线不一定是平行的． 解 设1T 为1a 到2a 的平行射影，2T 为2a 到3a 的平行射影，取3a 为1A 到2A 的延长线，取2A 与3A 重合，显 然，在1a 到3a 的仿射对应3112:a a T T →下，直线1a 和3a 上 的对应点的连线31A A 和31B B 不平行．２．在仿射对应下，若对应点之间连线相互平行，试问仿射对应是不是平行射影？ 解 由平行射影定义，对应点之间的连线平行于已知直线l ，即与方向l 平行，又因为对应点之间的连线平行，所以，对应点之间的连线都平行于方向l ，因此，是平行射影．３．在仿射对应下，圆的象是什么？ 解 椭圆．２．２ 仿射不变性与不变量1A 2A 3A 1a 2a 3a 1B2B 3B 题图第1经过平行射影不改变的性质和数，叫做仿射不变性质和仿射不变量． 经过仿射对应，它们也是不变的． 同素性和结合性都是仿射不变性质． 仿射对应把共点的线变成共点的线． 仿射对应把共线的点变成共线的点．定理２．１ 二直线间的平行性是仿射不变性质．即，两条平行直线经过仿射对应后仍然是平行直线．推论２．２ 平行四边形在仿射对应下还是平行四边形．即，平行四边形经过仿射对应后仍然是平行四边形．定义２．１ 简比（单比）．BCACABC =）（ 有向线段的数量之比． （１） 当C 在A ，B 之间时，0)(<ABC ； （２） 当C 在A ，B 之外时，0)(>ABC ； （３） 当A C =时，0)(=ABC ； （４） 当B C =时，∞=)(ABC ．定理２．３ 共线三点的简比是仿射不变量．即，共线三点的简比在仿射对应下不变．定理２．４ 两条平行线段的比是仿射不变量．即，两条平行线段的比在仿射对应下不变．定理２．５ 直线上两条线段的比是仿射不变量．即直线上两条线段的比在仿射对应下不变．注意：一般地，任意两条线段的比，不是仿射不变量．即，如果两条线段不平行，则它们的比在仿射对应下会改变．定理２．７ 在仿射对应下，任何一对对应三角形面积之比等于常数．即，任意两个三角形面积之比是仿射不变量．推论２．８ 任意两个多边形面积之比是仿射不变量．因此，任意两个图形面积之比是仿射不变量．A B C图定义1.2补充题 证明定理２．５ 直线上两条线段的比是仿射不变量．证明 如图，DC D A CD AD ''''=， 其中 CD CD BC AB CD AD ++=11+''''+=++=D C C B CD AB CD BC CD AB 1+''''+''''=''''+''+''=''''D C C B D C B A D C D C C B B A D C D A所以D C B A CD AB ''''=． 练习２－２１．证明：三角形的重心具有仿射不变性．解 因为共线三点的简比具有仿射不变性，所以，仿射对应把三角形中点变成中点；同素性和结合性都是仿射不变性质，仿射对应把共点的线变成共点的线，仿射对应把共线的点变成共线的点，所以，仿射对应把三角形的重心变成三角形重心．２．证明：平行四边形的重心具有仿射不变性． 解 同第１题．３．证明：梯形在仿射对应下仍为梯形．解 因为二直线的平行性是仿射不变性，所以，仿射对应把梯形的上下底变成梯形的上下底，因此，梯形在仿射变换下仍然变成梯形．４．证明：任意两个多边形面积之比是仿射不变量．解 将多边形划分成n 个三角形1S ，Λ,2S ，n S ，对应的划分得到对应的三角形1S '，Λ,2S '，n S '，由定理２．７，在仿射对应下，任何一对对应三角形面积之比等于常数．即，任意两个三角形面积之比是仿射不变量，所以有k S S S S S S nn ='=='='Λ2211，于是)(212121n n n S S S k S k S k S k S S S '++'+'='++'+'=+++ΛΛΛ 即k S S S S S S n n='++'+'+++ΛΛ2121A B C DA 'B 'C 'D '补充题图所以，任意两个多边形面积之比是仿射不变量．５．已知平面上的一条定直线l ，P 为平面上的任意一点，P 点的对应点P '是点P 关于直线l 的对称点，这种变换称为反射变换，定直线叫做它的轴．试证明：反射变换是仿射变换．解 因为平面上关于反射轴的对称点是唯一确定的，反射变换是平面到自身内的一一对应，所以，由仿射变换的定义，反射变换是仿射变换．２．３ 仿射变换的代数表达式知识点解析定理2．9 在仿射坐标系下，设共线三点A ，B ，C 的坐标为),(11y x ，),(22y x ，),(33y x ，则三点的交比为23132313)(y y y y x x x x BC AC ABC --=--==定理2．１０ 不共线的三对对应点决定唯一一个仿射变换．（见习题２－３第４题）． 解题指导 练习２－３１．在仿射坐标系下，证明直线的方程是一次方程． 证明 ［关键］ 利用仿射变换的式 ⎩⎨⎧++='++='ya x ab y ya x a a x 22211211［技巧］设直线方程b x k y '+'='，将仿射变换代入． 这时，得b y a x a a k y a x a b '+++=++)(12112221 整理得122212222111ka a b b ka x ka a a ka y -'+-+--=可见，仍为直线方程，即一次方程．２．求使三点)0,0(，)1,1(，)1,1(-的对应点分别为)3,2(，)5,2(，)7,3(-的仿射变换式．解 ［关键］ 将每对对应点分别代入仿射变换公式⎩⎨⎧++='++='y a x a b y ya x a a x 22211211 ［注意］ 仿射变换把点),(y x 变成),(y x ''时，有⎩⎨⎧++='++='ya x ab y ya x a a x 22211211 将每对对应点分别代入仿射变换公式⎩⎨⎧++='++='y a x a b y ya x a a x 22211211 得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=--+=++=++===2221121122211211735232a a b a a a a a b a a a b a解得⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧=-=-====6214213222122111a a a a b a代入仿射变换式，得所求的仿射变换式⎪⎩⎪⎨⎧+-='-+='yx y yx x 64321212３．利用仿射变换的表达式证明：直线上三点的简比是仿射不变量． 证明 ［关键］ 利用仿射变换的式⎩⎨⎧++='++='ya x ab y ya x a a x 22211211设三点),(11y x A ，),(22y x B ，),(33y x C 在仿射变换下分别变成),(11y x A '''，),(22y x B '''，),(33y x C '''，代入仿射变换式 ⎩⎨⎧++='++='ya x ab y ya x a a x 22211211 得322321322222121221211312311321221121121111y a x a b y y a x a b y y a x a b y y a x a a x y a x a a x y a x a a x ++='++='++='++='++='++='于是)()()()(23122311131213112313y y a x x a y y a x x a x x x x -+--+-='-''-' （*） 由定理２．９，k x x x x y y y y =--=--23132313即，)(2313y y k y y -=-，)(2313x x k x x -=-，代入（*）式得k y y a x x a y y k a x x k a x x x x =-+--+-='-''-')()()()(23122311231223112313同理k y y a x x a y y k a x x k a y y y y =-+--+-='-''-')()()()(23222321232223212313所以23132313x x x x y y y y '-''-'='-''-'即，直线上三点的简比是仿射不变量．４．利用解析方法证明：不共线的三对对应点决定一个仿射变换．证明 ［关键］ 利用仿射变换的式⎩⎨⎧++='++='ya x ab y ya x a a x 22211211设不共线的三点),(11y x A ，),(22y x B ，),(33y x C 在仿射变换下分别变成),(11y x A '''，),(22y x B '''，),(33y x C '''，代入仿射变换式 ⎩⎨⎧++='++='ya x ab y y a x a a x 22211211 得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++='++='++='++='++='++='322321331231132222212212211212212111121111y a x a b y y a x a a x y a x a b y y a x a a x ya x ab y y a x a a x 注意：三对对应点的坐标为已知数，a ，b ，11a ，12a ，21a ，22a 为未知数，写成矩阵形式为⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡''''''2221121133332222111133221110000011000000110000001a a b a a a y x y x y x y x y x y x y x y x y x 记作AX b =计算得212131312)])(())([(y y x x y y x x A ------= 这里0≠A ，因为如果0=A ，则0))(())((12131312=-----y y x x y y x x即12131213x x x x y y y y --=--这时),(11y x A ，),(22y x B ，),(33y x C 三点共线，与已知这三点不共线矛盾． 所以0≠A ．于是，方程组AX b =有唯一解．即，不共线三对对应点决定一个仿射变换．５．利用仿射变换导出椭圆12222=+by a x 的面积公式． 解 仿射变换把圆变成椭圆． 如图．由推论２．８，任意两个 图形面积的比是仿射不变量，有C B A ABCS S S S '''∆∆=椭圆圆b a rr S r ⋅⋅⋅⋅=2212212椭圆π于是ab S π=椭圆．２．４ 仿射变换的特例知识点解析 １． 平移变换把点),(y x P 平移到点),(y x Q ''，坐标关系式为⎩⎨⎧+='+='b y y ax x 平移变换保持线段的长度不变． ２．旋转变换以原点)0,0(O 为旋转中心，旋转角为θ，点),(y x P 旋转后变成),(y x P '''，坐标关系题图第5式为⎩⎨⎧+='-='θθθθcos sin sin cos y x y y x x其中⎥⎦⎤⎢⎣⎡-=θθθθcos sin sin cos A满足I A A A A ='='，即，A 为正交矩阵． ３． 反射变换在平面上取一定直线l ，使平面上的点P 对应到它关于直线l 的对称点P '，这样的变换叫做反射变换．直线l 上的点都是自对称点，称为反射变换的不动点． 直线l 称为反射对称轴． 坐标关系式为⎩⎨⎧-='='yy xx４．位似变换在平面上取一定点O 和一个非０常数k ，使O 对应自己，其它的点P 对应P '，三点O ，P ，P '在一条直线上，简比为k P OP =')(，⎩⎨⎧='='kyy kxx位似变换把直线变成与之平行的直线，把图形变成相似形． 解题指导 练习２－４１．求把点)3,0(变为点)4,2(-的平移变换，并将平移变换作用于曲线06432=--+y x x ．解 ［关键］ 将)3,0(P 和)4,2(-'P 代入平移变换公式⎩⎨⎧+='+='by y ax x ．得⎩⎨⎧+=+=-ba3402解得⎩⎨⎧=-=12b a于是，所求的平移变换为⎩⎨⎧+='-='12y y x x将平移变换作用于曲线06432=--+y x x ，就是将变换⎩⎨⎧+='-='12y y x x 的x ，y 解出来代入06432=--+y x x ，代入得08472=+'-'+'y x x２．求把点)3,2(-变为点)3,2(-的旋转变换，并将旋转变换作用于曲线06432=--+y x x ．解 把)3,2(-P 和)3,2(-'P 代入旋转变换公式⎩⎨⎧+='-='θθθθcos sin sin cos y x y y x x得⎩⎨⎧+-=---=θθθθcos 3sin 23sin 3cos 22解得0sin =θ， 1cos -=θ 再代入旋转变换公式得⎩⎨⎧-='-='y y xx将这个变换作用于曲线06432=--+y x x ，就是将变换⎩⎨⎧-='-='yy xx 的x ，y 解出来代入06432=--+y x x ，代入得06432=-'+'-'y x x３．求中心在原点，半轴分别为1和２并以直线025=-y x 为对称轴的椭圆方程． 解 1=a ，2=b ，中心在原点的椭圆方程为1422=+y x对称轴为025=-y x ，即x y 52=，这时，25tan ==θk于是292tan 11cos 2=+=θθ，295cos 1sin 2=-=θθ，所以，旋转方程为⎪⎪⎩⎪⎪⎨⎧+='-='292295295292y x y y x x于是⎪⎪⎩⎪⎪⎨⎧'+'='+'=292295295292y x y y x x 代入1422=+y x ，得0116601044122=-''+'+'y x y x ．４．证明：位似变换把直线变成直线．证明 ［关键］设直线b ax y +=，从位似变换⎩⎨⎧='='ky y kx x 中解出x ，y 代入直线b ax y +=内．代入得kb x a y +'='显然仍为一条直线．５．证明：位似变换把直线变成与自己平行的直线．证明 由第４题结果可知，位似变换把直线b ax y +=变成直线kb x a y +'='，因为斜率都为a ，所以二者平行．。

include "opencv2/highgui.hpp" #include "opencv2/imgproc.hpp" #include <iostream> #include <stdio.h>
#
using namespace cv; using namespace std; /// Global variables char* source_window = "Source image"; char* warp_window = "Warp"; char* warp_rotate_window = "Warp + Rotate"; /** @function main */
/// Set your 3 points to lculate the Affine Transform srcTri[0] = Point2f( 0,0 ); srcTri[1] = Point2f( src.cols - 1, 0 ); srcTri[2] = Point2f( 0, src.rows - 1 );
• /// Get the rotation matrix with the specifications above • rot_mat = getRotationMatrix2D( center, angle, scale ); • • • • • • • /// Rotate the warped image warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() ); /// Show what you got namedWindow( source_window, CV_WINDOW_AUTOSIZE ); imshow( source_window, src ); namedWindow( warp_window, CV_WINDOW_AUTOSIZE ); imshow( warp_window, warp_dst );

仿射变换的基本公式及参数估算方法基本变换公式我们考虑二维平面的仿射变换；缩放，旋转，平移变换；假设两个点P1(x1,y1),p2(x2,y2) 经过仿射变换后变为 P1'(x1',y1'),P2'(x2',y2')1.假如只有缩放变换，比例为s，则 x1' = s * x1 y1' = s * y1 x2',y2'同理2.假如只有旋转变换，旋转角度为theta，则 x1' = x1 * cos(theta) + y1 *sin(theta) y1' = -x1 * sinn(theta) + y1 * cos(theta) x2',y2'同理 3 假如只有平移变换，平移(dx,dy)，则 x1' = x1 + dx y1' = y1 + dy x2',y2'同理不变性1.如果只有旋转和平移变换，两个点之间的距离仍然保持不变；即如果只经过旋转和平移变换；P1P2 之间的距离和 P1'P2'之间的距离相等；平移变换不证明了，旋转变换下通过旋转公式，计算 (x1' - x2')^2 + (y1'-y2')^2 易得： (x1' - x2')^2 + (y1'-y2')^2 = (x1 - x2)^2 + (y1-y2)^22.如果只有缩放和平移变换，向量 P1P2 和向量 P1'P2' 平行；向量 P1P2可表示为：(x2-x1,y2-y1) 向量P1'P2'可表示为(x2'-x1', y2'-y1')；向量 P1P2 和向量 P1'P2' 平行可表示为: (x2-x1)(y2'-y1') - (x2'-x1')(y2-y1) = 0参数估算回推1.利用不变性以及特征点来匹配来推算变换参数；估算顺序需要为缩放-> 旋转 -> 平移；参见参考资料；2.利用LM等优化算法以及RANSAC等一致性算法来优化参数以及排除外点如果两张图之间只有仿射变换，那么在通过特征点匹配算法得到两张图之间的匹配关系后；我们如何进行仿射变换参数的估量？一种通用方法是将变换整体考虑，例如计算单应矩阵，然后根据单应矩阵推算仿射变换参数但是在一些场景下，例如我们需要一些快速算法，或者一些可解释性的场景，我们可以利用仿射变换的性质分别进行缩放/旋转/平移参数的估算缩放参数估算缩放和旋转参数需要首先进行估算；其一，缩放参数不受旋转和平移参数的影响，其次，缩放参数会影响旋转和平移参数的估算；•缩放不变性缩放不变性指缩放参数不受旋转和平移参数的影响，两个特征点之间的距离即可代表两张图的缩放比例•一个误区之前觉得可以以一个特征点在两张图中不同的坐标到图像中心的距离来代表两张图之间的缩放比例，后来发现问题很大，主要问题是图像经过仿射变换后图像的中心点发生了偏移，只能是匹配的特征点之间的距离才能代表两图之间的缩放比例。

仿射变换的步骤仿射变换是一种在几何学和图像处理中常用的技术，可以通过变换矩阵来改变图像的形状、大小、方向和位置。

本文将介绍仿射变换的步骤，并提供一些实用的指导意义。

步骤一：选择合适的变换类型仿射变换包括平移、旋转、缩放和剪切等多种类型。

在进行仿射变换之前，我们需要根据需要选择合适的变换类型。

例如，如果想要将一幅图像向右平移，就需要使用平移变换。

步骤二：确定变换矩阵变换矩阵是描述仿射变换的数学工具。

不同的变换类型对应不同的变换矩阵。

例如，平移变换的变换矩阵如下所示：```[1 0 tx][0 1 ty]```其中，tx和ty分别代表水平和垂直方向的平移量。

步骤三：应用变换矩阵将变换矩阵应用于需要进行变换的图像上。

对于平移变换，我们可以通过将每个像素点的坐标偏移tx和ty来实现。

对于其他类型的变换也可采取相应的操作方法。

步骤四：处理边界条件在进行仿射变换时，可能会出现图像边界溢出的情况。

为了保持图像的完整性，我们可以通过插值算法对溢出的像素进行合理的处理，例如最近邻插值或双线性插值。

步骤五：调整图像大小有时候，进行变换后的图像大小可能发生变化。

为了保持图像的原始比例，我们可以根据需要进行图像的缩放或裁剪。

步骤六：可选的后处理根据具体需求，我们还可以对进行仿射变换后的图像进行一些后处理操作，例如图像增强、边缘检测或特征提取等。

在实际应用中，仿射变换具有广泛的用途。

例如，在计算机视觉中，通过仿射变换可以实现图像的校正、纠正透视畸变、匹配图像等。

在图形处理中，可利用仿射变换来生成平铺效果、形变效果等。

总之，仿射变换是一种非常有用的技术，通过简单的步骤和变换矩阵，我们可以实现图像的形状改变、位置移动和旋转等操作。

熟练掌握仿射变换的步骤和应用场景，能够为我们的几何学和图像处理工作提供很大的帮助。

仿射变换公式《仿射变换公式》的研究是数学的一个重要分支，它是指在指定的空间中改变物体形状的方式。

仿射变换又称作坐标变换，它是一类非线性变换，可以将任意空间中的点移动到一个新的位置，其中可以包括旋转、移动和缩放。

关于仿射变换，有一个多元一次方程组，它可以表述仿射变换在任意物体上的映射关系，而对于任意变换，都可以用仿射变换表示，因此仿射变换在很多地方有着广泛的应用。

首先，仿射变换可以分为三种：缩放变换、旋转变换和平移变换。

1、缩放变换：指的是把一个多边形的位置改变为更大或更小的位置，它是在一个特定的坐标系不变的情况下进行的，它的公式可以写为：$x=sx,quad y=sy$其中，$(xy$为变换后的坐标，$(x,y)$为变换前的坐标，s为缩放比例。

2、旋转变换：指的是把一个多边形通过旋转变换成另一个任意形状的变换，它的公式可以写为：$x=xcosalpha-ysinalpha,quad y=xsinalpha+ycosalpha$ 其中，$(xy$为变换后的坐标，$(x,y)$为变换前的坐标，$alpha$为旋转角度。

3、平移变换：指的是把多边形从一个点移动到另一个点的变换，它的公式可以写为：$x=x+h,quad y=y+k$其中，$(xy$为变换后的坐标，$(x,y)$为变换前的坐标， h为横坐标的偏移量，k为纵坐标的偏移量。

上述三种变换是最常见的，但是它们只是仿射变换的一部分，仿射变换可以用以下公式表达：$x=ax+by+h,quad y=cx+dy+k$其中，$(xy$为变换后的坐标，$(x,y)$为变换前的坐标，a,b,c,d,h,k为变换系数。

仿射变换的应用也是非常广泛的，在平面图形的绘制及分析，几何变换的研究，图像处理等方面都有重要的应用，从历史上看，古希腊几何学家就研究过仿射变换。

在大量的数据处理以及图像处理中，仿射变换是最常用的变换之一，因为仿射变换可以保证多边形的完整性，也可以保持多边形形状的尺寸比例不变。