列举法求概率

用列举法求概率
列举法是一种基于所有可能性的方法，用于求解概率。

对于一个随机试验，可以通过列举出所有可能的结果，然后计算感兴趣事件发生的次数，再除以总的可能性数目来计算概率。

以下是使用列举法求解概率的步骤：
1.确定随机试验的所有可能结果。

这些结果应该是互不相同
且穷尽的。

2.计算感兴趣事件发生的次数。

根据实际情况，确定符合感
兴趣条件的结果个数。

3.计算总的可能性数目。

确定随机试验的总结果数目。

4.使用公式 P(A) = n(A) / n(S) 计算概率。

其中，P(A)表示感兴
趣事件发生的概率，n(A)表示感兴趣事件发生的次数，n(S)表示总的可能性数目。

例如，考虑一枚标准硬币的抛掷，求得正面向上的概率。

1.所有可能的结果是正面向上和反面向上。

2.感兴趣事件是正面向上。

3.总的可能性数目是2。

4.使用公式 P(A) = n(A) / n(S) ，其中 n(A) = 1（因为正面向上
只有一种可能），n(S) = 2。

P(正面向上) = 1 / 2 = 0.5
因此，得到正面向上的概率为0.5或50%。

使用列举法求解概率可以简单直观地计算概率，尤其适用于样
本空间较小且结果可列举的情况。

然而，对于复杂的问题或较大的样本空间，列举法可能不切实际，此时可以选择其他概率计算方法，如频率法或概率模型。

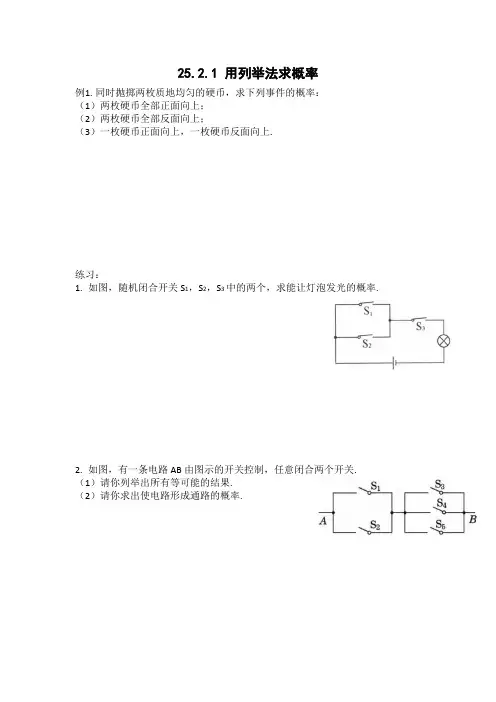
25.2.1 用列举法求概率例1.同时抛掷两枚质地均匀的硬币，求下列事件的概率：（1）两枚硬币全部正面向上；（2）两枚硬币全部反面向上；（3）一枚硬币正面向上，一枚硬币反面向上.练习：1.如图，随机闭合开关S1，S2，S3中的两个，求能让灯泡发光的概率.2.如图，有一条电路AB由图示的开关控制，任意闭合两个开关.（1）请你列举出所有等可能的结果.（2）请你求出使电路形成通路的概率.3.一口袋中有四根长度分别为1cm，3cm，4cm和5cm的细木棒，小明手中有一根长度为3cm的细木棒，现随机从袋内取出两根细木棒与小明手中的细木棒放在一起，回答下列问题:(1)求这三根细木棒能构成三角形的概率；(2)求这三根细木棒能构成直角三角形的概率；(3)求这三根细木成等腰三角形的概率.25.2.2 用列表法求概率例2.同时掷两枚质地均匀的骰子，求下列事件的概率：（1）两枚骰子的点数相同；（2）两枚骰子点数的和是9；（3）至少有一枚骰子的点数为2.例题（放回问题）（2017年省卷19题）在一个不透明的盒子中，装有3个分别写有数字6，-2,7的小球，他们的形状、大小、质地完全相同，搅拌均匀后，先从盒子里随机抽取1个小球，记下小球上的数字后放回盒子，搅拌均匀后再随机取出1个小球，再记下小球上的数字.(1) 用列表法或树状图法(树状图也称树形图)中的一种方法，写出所有可能出现的结果；(2) 求两次取出的小球上的数字相同的概率P.例题（不放回问题）（2018年省卷19题）将正面分别写着数字1，2，3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同，若背面向上放在桌面上，这三张卡片看上去无任何差别)洗匀后，背面向上放在桌面上，从中先随机抽取一张卡片，记该卡片上的数字为x；再把剩下的两张卡片洗匀后，背面向上放在桌面上，再从这两张卡片中随机抽取一张卡片，记该卡片上的数字为y.(1) 用列表法或树状图法(树状图也称树形图)中的一种方法，写出所有可能出现的结果；(2) 求取出的两张卡片上的数字之和为偶数的概率P.练习：1.（2020年省卷19题）甲、乙两个家庭来到以“生态资源，绿色旅游”为产业的美丽云南，各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游。

用列举法求概率
用列举法求概率指的是通过对事件包含的所有可能情况进行数量计算，从而得出该事件发生的概率。

它可以用来计算单个或多个独立事件的概率。

一般步骤如下：
（1）首先确定所要求的概率事件；
（2）然后将该事件分解成一个或多个独立事件；
（3）根据独立事件的可能性，将所有可能的结果列举出来；
（4）统计满足条件的可能性的数量；
（5）最后计算出概率值。

例如：在一副有52张牌的扑克牌中抽出一张，问抽到的是黑桃的概率。

（1）首先确定所要求的概率事件：抽到的是黑桃
（2）将该事件分解成一个独立事件：抽到的是黑色；抽到的是桃子
（3）根据独立事件的可能性，将所有可能的结果列举出来：抽到的是黑桃、黑红桃、黑方块、红桃、红红桃、红方块、梅花、梅红桃、梅方块；
（4）统计满足条件的可能性的数量：抽到的是黑桃的可能性有1种；
（5）最后计算出概率值：P(抽到的是黑桃)=1/9=0.11。

人教版数学九年级上册25.2《列举法求概率》教案一. 教材分析《列举法求概率》是人教版数学九年级上册第25.2节的内容，主要介绍了利用列举法求概率的方法。

本节内容是在学生掌握了概率的基本概念和等可能事件的概率求法的基础上进行的，是进一步培养学生解决实际问题的能力。

通过本节内容的学习，学生能够掌握列举法求概率的步骤和方法，并能运用到实际问题中。

二. 学情分析九年级的学生已经具备了一定的逻辑思维能力和解决问题的能力，对于概率的基本概念和等可能事件的概率求法已经有了一定的了解。

但是，学生在运用列举法求概率时，可能会出现列举不完整、分类不清晰等问题。

因此，在教学过程中，需要引导学生正确地进行列举和分类，培养学生解决问题的能力。

三. 教学目标1.知识与技能：使学生掌握列举法求概率的方法，能够运用列举法解决实际问题。

2.过程与方法：通过学生的自主探究和合作交流，培养学生的解决问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队合作意识。

四. 教学重难点1.重点：列举法求概率的方法。

2.难点：如何引导学生正确地进行列举和分类，解决实际问题。

五. 教学方法1.情境教学法：通过生活实例的引入，激发学生的学习兴趣，引导学生运用列举法解决实际问题。

2.合作学习法：学生进行小组讨论和合作交流，培养学生解决问题的能力和团队合作意识。

3.引导发现法：教师引导学生进行自主探究，发现列举法求概率的方法，培养学生的独立思考能力。

六. 教学准备1.教学课件：制作相关的教学课件，帮助学生更好地理解和掌握列举法求概率的方法。

2.练习题：准备一些相关的练习题，用于巩固学生的学习效果。

七. 教学过程1.导入（5分钟）利用生活实例引入本节课的内容，例如抛硬币、抽奖等，引导学生思考如何求解这些事件的概率。

2.呈现（10分钟）通过课件展示列举法求概率的步骤和方法，引导学生理解并掌握列举法的基本原理。

3.操练（10分钟）让学生进行小组讨论，共同解决一些实际问题，例如抛硬币三次，求正面向上的概率等。

.求概率的方法在新课标实施以来，中考数学试题中加大了统计与概率局部的考察，表达了“学以致用〞这一理念． 计算简单事件发生的概率是重点，常用的方法有:列举法、列表法、画树状图法，这三种方法应该熟练掌握，先就有关问题加以分析． 一、列举法 例1：〔05济南〕如图1所示，打算了三张大小相同的纸片，其中两张纸片上各画一个半径相等的半圆，另一张纸片上画一个正方形．将这三张纸片放在一个盒子里摇匀，随机地抽取两张纸片，假设可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢；假设可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢．你认为这个游戏对双方是公平的吗？假设不是，有利于谁？ ．分析：这个游戏不公平，因为抽取两张纸片，全部时机均等的结果为：半圆半圆，半圆正方形，正方形半圆，正方形正方形．所以取出的两张纸片都画有半圆形的概率为41． 取出的一张纸片画有半圆、一张画有正方形的概率为2142=，因为二者概率不等，所以游戏不公平． 说明: 此题采纳了一种较为有趣的试题背景，重在考查学生对概率模型的理解、以及对不确定事件发生概率值的计算．此题用列举方法，也可以用画树状图，列表法． 二、画树状图法 例2：〔06临安市〕不透明的口袋里装有白、黄、蓝三种颜色的乒乓球〔除颜色外其余都相同〕，其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为12．〔1〕试求袋中蓝球的个数．〔2〕第一次任意摸一个球〔不放回〕，第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．解析：⑴设蓝球个数为x 个，则由题意得21122=++x ， 1=x答：蓝球有1个． 〔2〕树状图如下：∴ 两次摸到都是白球的概率 =61122=． 说明:解有关的概率问题首先弄清：①需要关注的是发生哪个或哪些结果．②无论哪种都是时机均等的，要对实践的分析得出概率通常用列表或画树状图来写出事件发生的结果，这样便于确定相关的概率． 此题是考查用树状图来求概率的方法，这种方法比拟直观，把全部可能的结果都一一排列出来，便于计算结果． 三、列表法 例3：〔06晋江市〕如图2，是由转盘和箭头组成的两个装置，装置A 、B 的转盘分别被平均分成三局部，装置A 上的数字是3、6、8；装置B 上的数字是4、5、7；这两个装置除了外表数字不同外，其他构造均相同，小东和小明分别同时转动A 、B 两个转盘〔一人转一个〕，如果我们规定箭头停留在较大数字的一方获胜〔如：假设A 、B 两个转盘的箭头分别停在6、4上，则小东获胜，假设箭头恰好停在分界图1 5 4 B768A 3图2.线上，则重新转一次〕，请用树状图或列表加以分析说明这个游戏公平吗？ 解析：〔方法一〕画树状图： 由上图可知，全部等可能的结果共有9种，小东获胜的概率为95，小明获胜的概率为94，所以游戏不公平．由上表可知，全部等可能结果共有9种，小东获胜的概率为95，小明获胜的概率为94，所以游戏不公平．说明：用树状图法或列表法列举出的结果一目了然，当事件要经过屡次步骤〔三步以上)完成时，用这两种方法求事件的概率很有效．6开始。