初中数学常见几何基本模型——双子型
- 格式:doc
- 大小:446.00 KB
- 文档页数:3
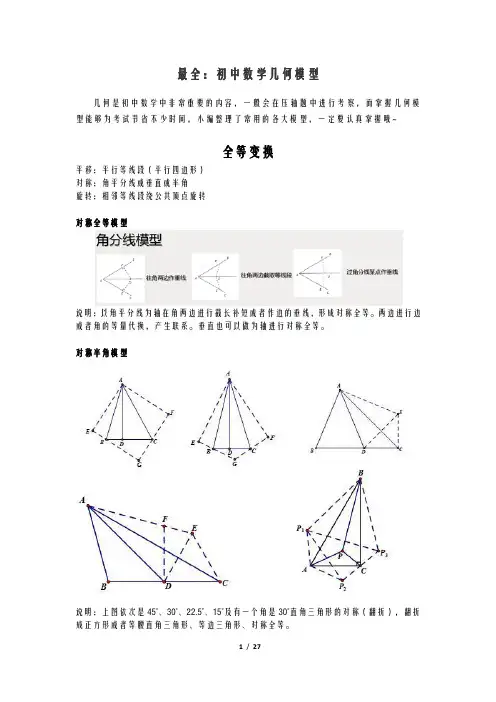
最全:初中数学几何模型几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,小编整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形;遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等;遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

2018-2019学年九年级数学初中常见几何模型汇总(图片版)第一篇:2018-2019学年九年级数学初中常见几何模型汇总(图片版) 初中常见几何模型汇总全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变换说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

初中几何48种数学模型系统讲解初中几何是数学中非常重要的一个分支,涉及到许多基础知识和技能。
在初中几何学习中,数学模型是非常重要的一环,它能够帮助学生更好地理解和掌握几何知识,并提高解题的能力。
下面我们就来介绍一下初中几何中常见的48种数学模型系统。
1. 平面几何模型:平面几何模型是研究平面上的图形和变换的数学模型,例如平移、旋转、对称等。
2. 立体几何模型:立体几何模型是研究空间中的图形和变换的数学模型,例如立体的投影、旋转、平移等。
3. 直线模型:直线模型是用来表示直线的数学模型,例如在平面几何中,可以使用坐标系来表示一条直线。
4. 线段模型:线段模型是用来表示线段的数学模型,例如在平面几何中,可以使用坐标系来表示一条线段。
5. 角度模型:角度模型是用来表示角度的数学模型,例如在平面几何中,可以使用角度制和弧度制来表示角度。
6. 相交模型:相交模型是用来表示图形相交的数学模型,例如在平面几何中,可以使用交点来表示两条直线相交的情况。
7. 平行模型:平行模型是用来表示平行线的数学模型,例如在平面几何中,可以使用平行线的定义来表示两条直线平行的情况。
8. 垂直模型:垂直模型是用来表示垂直线的数学模型,例如在平面几何中,可以使用垂直线的定义来表示两条直线垂直的情况。
9. 对称模型:对称模型是用来表示对称图形的数学模型,例如在平面几何中,可以使用对称轴来表示对称图形的情况。
10. 相似模型:相似模型是用来表示相似图形的数学模型,例如在平面几何中,可以使用相似比例来表示两个相似图形之间的关系。
11. 等比模型:等比模型是用来表示等比数列的数学模型,例如在几何中,可以使用等比数列来表示一些几何问题。
12. 等分模型:等分模型是用来表示等分线段的数学模型,例如在几何中,可以使用等分线段来表示将一个线段分成若干等分的情况。
13. 圆模型:圆模型是用来表示圆形的数学模型,例如在平面几何中,可以使用圆心、半径来表示一个圆。

初二数学30个重点几何模型初二数学重点几何模型一、直线与角直线是几何中最基本的概念之一。
直线无法直接测量,但可以通过两个点的连线得到一条直线。
直线没有宽度和长度,只有方向。
在几何中,直线通常用字母表示。
角是由两条直线共享一个公共端点而形成的图形。
角度用度数来衡量,通常用小圆圈表示。
角度可以分为钝角、直角、锐角和平角四种类型。
钝角大于90度,直角等于90度,锐角小于90度,平角等于180度。
二、三角形三角形是由三条线段相连而形成的多边形。
三角形有很多种类,包括等边三角形、等腰三角形和直角三角形等。
等边三角形的三条边长度相等,等腰三角形的两条边长度相等,直角三角形则有一个角度等于90度。
三、四边形四边形是由四条线段相连而形成的多边形。
四边形有很多种类,包括正方形、矩形、平行四边形等。
正方形的四条边长度相等且四个角都是直角,矩形的四个角都是直角,平行四边形的对边平行且长度相等。
四、圆与圆周圆是一个平面上所有点到一个固定点的距离都相等的图形。
圆周是圆的边界,也是圆的周长。
圆周上的任意两点与圆心相连,形成的线段称为弦。
圆周上的任意点与圆心相连,形成的线段称为半径。
圆周上的任意两点与圆心相连,形成的线段称为直径。
五、多边形多边形是由多条线段相连而形成的封闭图形。
多边形的边数可以是任意大于等于3的整数。
多边形根据边的长度或角的大小可以分为等边多边形、等角多边形和正多边形等。
等边多边形的所有边长度相等,等角多边形的所有角度相等,正多边形既是等边多边形又是等角多边形。
六、相似与全等相似是指两个图形的形状相似,但大小不同。
相似的图形具有对应角度相等和对应边成比例的特点。
全等是指两个图形的形状和大小完全相同。
全等的图形具有对应边相等和对应角度相等的特点。
七、平面镜与对称平面镜是一种可以反射光线的镜子。
平面镜的特点是光线入射角等于反射角,入射光线、反射光线和法线三者在同一平面上。
对称是指图形通过某个中心轴线或中心点对折后,两边或两部分完全重合。

初中数学常见几何模型—基本模型法前言个人对数学基本模型法的定义是,从一些复杂的图形中,找出部分简单常见图形的过程,所以后面总结的模型,不一定是题目中完整的图,只是题中部分图形而已。
部分模型的一般情况,在这份讲义没有做练习的整理,另外还有最短路径模型、二倍角模型、补全法等部分模型没有整理,如果全部放在一起内容太多,另外因为部分模型应用较广,可能涉及到初二下和初三的内容,如果是在初二上期中复习用的话,请老师们自行筛选。
一、双垂直模型(角相等)如图:则有:∠ACD=∠B 则有:∠2=∠3练习1、如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为()练习2、已知:AB⊥BC于B,EF⊥AC于G, DF⊥BC于D,BC=DF,AC等于EF吗?,说明理由。
二、三垂直模型(弦图模型、一线三等角特殊情况)练习:1、在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、3、3.5,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=()A.7.5 B.6.5 C.4.5 D.4 2.如图,△ABC是等腰直角三角形,DE过直角顶点A,∠D=∠E=90°,则下列结论正确的个数有()①CD=AE;②∠1=∠2;③∠3=∠4;④AD=BE.A.1个B.2个C.3个D.4个3.如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为()A.4cm B.8cm C.9cm D.10cm 4、如图①所示,在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN.(2)如图②.若过点C直线MN与线段AB相交,AM⊥MN于点M,BN⊥M N于N,(1)中的结论是否仍然成立?说明理由.图①图②5、如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠DAB(2)试说明线段DM与AM有怎样的位置关系?(3)线段CD、AB、AD间有怎样的关系?直接写出结果。
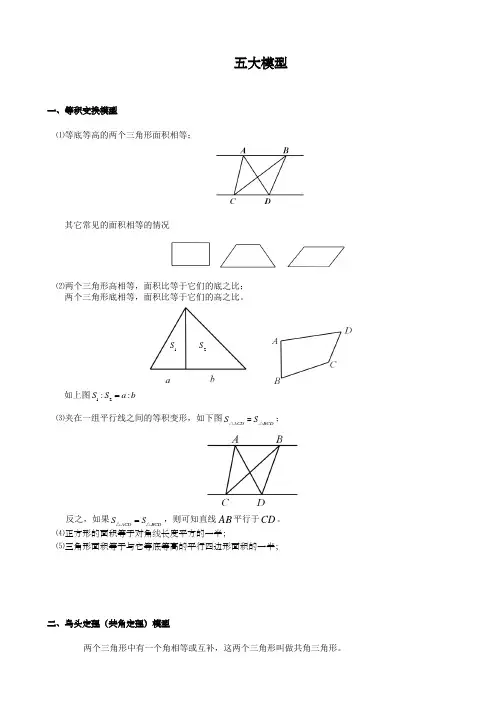
一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
五大模型1S 2S共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型①AD AE DE AFAB AC BC AG===; ②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方。
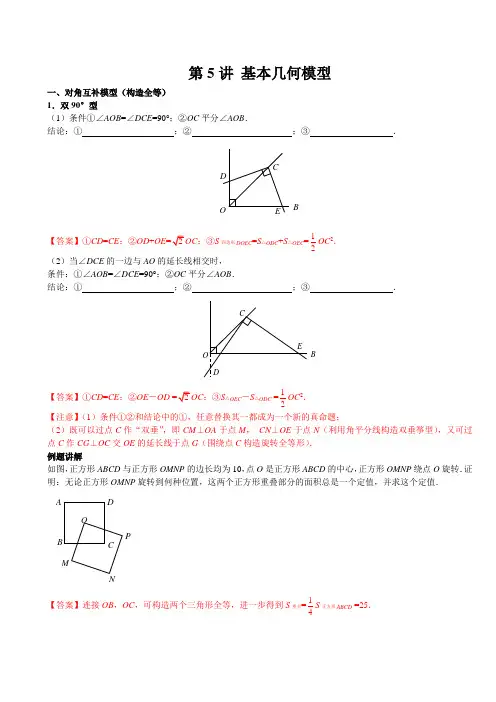
第5讲 基本几何模型一、对角互补模型(构造全等) 1.双90°型(1)条件①∠AOB =∠DCE =90°;②OC 平分∠AOB .结论:① ;② ;③ .DBCO E【答案】①CD =CE ;②OD +OE;③S 四边形DOEC =S △ODC +S △OEC =12OC 2. (2)当∠DCE 的一边与AO 的延长线相交时, 条件:①∠AOB =∠DCE =90°;②OC 平分∠AOB .结论:① ;② ;③ .O EDBC【答案】①CD =CE ;②OE -OD;③S △OEC -S △ODC =12OC 2. 【注意】(1)条件①②和结论中的①,任意替换其一都成为一个新的真命题; (2)既可以过点C 作“双垂”,即CM ⊥OA 于点M , CN ⊥OE 于点N (利用角平分线构造双垂筝型),又可过点C 作CG ⊥OC 交OE 的延长线于点G (围绕点C 构造旋转全等形). 例题讲解 如图,正方形ABCD 与正方形OMNP 的边长均为10,点O 是正方形ABCD 的中心,正方形OMNP 绕点O 旋转.证明:无论正方形OMNP 旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值. O P MN B CDA【答案】连接OB ,OC ,可构造两个三角形全等,进一步得到S 重合=14S 正方形ABCD =25.2.60°,120°型(1)条件:①∠AOB =2∠DCE =120°;②OC 平分∠AOB .结论:① ;② ;③ .OE DCBA答案:①CD =C E ;②OD +OE =OC ;③ S 四边形DOEC =S △ODC + S △OEC =2 (2)当∠DCE 的一边与AO 的延长线相交时. 条件:①∠AOB =2∠DCE =120°;②OC 平分∠AOB . 结论:① ;② ;③ .OE DCBA答案:①CD =C E ;②OE - OD +=OC ;③ S 四边形DOEC = S △OEC -S △ODC +=2. 【注意】(1)条件①②和结论中的①,任意替换其一都能成为一个新命题;(2)既可以过点C 作“双垂”,即CM ⊥OA 于点M ,CN ⊥OE 于点N (利用角平分线构造双垂筝型),又可以OC 为边,构造等边△OCG ,或将线段CO 绕点C 逆时针旋转60°(围绕点C 构造旋转全等形). 例题讲解把两个边长都等于4的等边三角形拼成菱形ABCD (如下图).有一个含60°角的三角尺,使三角尺的60°角的顶点与点A 重合,两边分别与AB ,AC 重合.(1)将三角尺绕点A 按逆时针方向旋转,当三角尺的两边分别与菱形的两边BC ,CD 相交于点E ,F 时(如图1),通过观察或测量AE ,AF 的长度,你能得出什么结论?并证明你的结论;(2)在旋转过程中四边形AECF 的周长是否发生变化?如果没有变化,请说明理由;如果有变化,请求出周长的最小值;(3)若将(1)中三角尺的60°角的顶点P 在AC 上移动且与点A 、C 都不重合,三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时(如图2),那么PE 、PF 之间又有什么数量关系?并证明你的结论.答案:(1)AE =AF ,可证△ABE ≌△ACF (ASA )(2)四边形AECF 的周长=2AE +CE +CF =2AE +BC =2AE +4.当AE ⊥BC 时,AE 有最小值,故四边形AECF 的周长的最小值为4;(在旋转过程中四边形AECF 的面积不发生变化) (3)PE =PF (过点P 利用角平分线构造双垂筝型全等).二、角含半角模型(必旋转)1、条件:①正方形ABCD ;②∠EAF =45°.结论:① ;② .图①E D CF答案:结论:DF +BE =EF 或DF -DE =EF . 如题图①,将△ADF 绕点A 顺时针旋转90°到△ABG 的位置,此时C ,B ,G 共线; 如题图②,将△ABE 绕点A 顺时针旋转90°到△ADG 的位置,此时D ,G ,C 共线; 【注意】(1)但凡旋转,必然有边对应相等,只需用圆规将共旋转点、边旋转过去即可: (2) 旋转后.往往涉及三点共线问题(须简单证明之);(3) 旋转后,一般需要再证一对共旋转点的三角形全 等 (SAS ).例题讲解如图,在平面直角坐标中,边长为2的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上,O 为坐标原点.现将正方形OABC 绕O 点顺时针旋转,旋转角为θ,当A点第一次落在直线y =x 上时停止旋转,旋转过程中,AB 边交直线y =x 于点M ,BC 边交x 轴于点N . (1)当A 点第一次落在直线y =x 上时,求点A ,B 两点坐标(直接写出结果);(2)设△MBN 的周长为p ,在旋转正方形OABC 的过程中,p 值是否有变化?请证明你的结论.答案:(1)(2)p值不会发生变化,将△OAM绕点O顺时针旋转90°到△OCG的位置,此时B,C,G三点共线,得MN==BM+CN,∴△MBN的周长p=MN+BM+BN=AM+CN+BM+NB=2AB=4.变式1:如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于M交AC于点N,连接MN,则△AMN的周长C答案:将△BDM绕点D顺时针旋转120°到△CDE的位置,此时A,C,E三点共线,得MN=BM+CN,∴△AMN 的周长为:AM+MN+AN=AM+BM+CN+AN=2AB=6.变式2ACF答案:EF=DE+BF.将△ADE绕点A旋转到△CDE的位置,此时C,B,G共线(或延长CB至点G,使BG=DE),再证△AFG≌△AFE (SAS),可得EF=FG=BG+BF=DE+BF.2.条件:①等腰Rt△ABC中;②∠DAE=45°.结论:.图①BC图②答案:222BD CE DF +=.图①FBC图②如图①②,将△ACE 绕点A 按顺时针旋转90°到△AB F 的位置,此时FB ⊥BC ,连接DF ,可证△ADF ≌△ADE (SAS ),于是DF =DE .在Rt △FBD 中,由勾股定理可知222FB BD DF +=,进一步得到222BD CE DF +=变式1:已知在△ABC 中,∠BAC =45°,AD ⊥BC 于点D ,若BD =6,CD =4,求△ABC 的面积.DC答案:法1:过点B 作BF ⊥AC 于点F ,如图①所示,∴△AFE ≌△BFC (ASA ),∴AE =BC =10. 又由△BDE ∽△BFC (ASA),∴BD AD DE CD =,∴6104DEDE +=,∴DE =2,则AD =12,∴S △ABC =60. 变式1图①C变式1图②ED CB法2:以D 为圆心,DA 长为半径画弧,交直线BC 于E ,F 两点(以AD 为高,构造等腰△AEF ),如图②所示,利用“角含半角模型”知道222BE CF BC +=,有222(BE 2)10BE ++=,∴BE =6,AD =DE =12,∴S △ABC =60.变式2:如图,等边△ABC 中,点P ,Q 在BC 边上,且∠P AQ =30°.若BP =2,QC =3,求AB 的长.答案:将△ABP 绕点A 按顺时针旋转60°至△ACD 的位置,过点D 作DE ⊥BC 于点E .在Rt △DEC 中,DC在Rt △又可证△AQP ≌△AQD (SAS ), 得PQ=DQ ∴BC =AB =5三、一线三等角模型如图①,∠ABC =∠ACE =∠CDE =90°; 如图②,∠ABC =∠ACE =∠CDE =60°; 如图③,∠ABC =∠ACE =∠CDE =45°.图①C E图②BEC图③ABDC例题讲解1.△ABC 和△DEF 均为正三角形,E 是BC 边的中点.(1)如图①,DE 交AB 于点M ,EF 交AC 于点N ,求证:△BEM ∽△CNE ;(2)如图②,将△DEF 绕点E 旋转,使得DE 交BA 的延长线于点M ,EF 交AC 于点N ,则第(1)题的结论是否依旧成立?图1E BF图2E FB【答案】答案略(可再追问证明△CEN ∽△EMN ).2.如图,将等边△ABC 折叠,使得点C 落在AB 边上的点D 处,折痕为EF ,点E ,F 分别在AC 和BC 边上.若AC =8,AD =2,则CF :CE 的值为________.第2题图C A BD【答案】7:5简答:由翻折知CE DECF DF=,再由“一线三等角模型”可知△ADE ∽△BFD ,根据“相似三角形的周长之比等于相似比”得ADE DEBFD DF=△△,而△ADE 的周长=AC +AD =10,△BFD 的周长=BC +BD =14,∴57CE DE CF DF ==.变式1:如图,在等边△ABC 中,D 是BC 边上一点,且BD :DC =1:3,把△ABC 折叠,使点A 落在BC 边上的点D 处,那么AM :AN 的值为________.变式1图A CB D【答案】5:7变式2:如图,在平面直角坐标系中,O (0,0),A (6,,B (12,0).将△OAB 沿直线CD 折叠,使点A 恰好落在线段OB 上的点E 处.若OE =245,则CE :DE 的值是________.变式2图【答案】提示:先证△OAB 为等边三角形,后面方法同例2. 四、K 字模型探究在学习几何知识时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K 字型是非常重要的基本图形,可以建立如下的“模块”(如图①):图1A DCB(1)已知∠A =∠D =∠BCE =90°,则△ABC ∽△DCE ;请就图①证明上述“模块”的合理性; 【答案】略(2)请直接利用上述“模块”的结论解决下面两个问题: (i )如图②,已知点A (-2,1),点B 在直线y =-2x +3上运动,若∠AOB =90°,求此时点B 的坐标;图2A【答案】(i )过点A 作AD ⊥x 轴于点D ,过点B 作BE ⊥x 轴于点E ,可证△ODA ∽△BEO , ∴AD OEOD BE=. 点B 在直线y =-2x +3上,可设B (m ,-2m +3), ∴1=223m m -+,∴34m =.故3342B ⎛⎫ ⎪⎝⎭,.(ii )如图③,过点A (-2,1)分别作与x 轴,y 轴平行的线,交直线y =-2x +3于点C ,D ,求点A 关于直线CD 的对称点E 的坐标.图3【答案】(ii )过点E 作EG ∥y 轴,过点D 作DF ⊥FG 于点F ,延长AC 交FE 于点G (构造“K 字模型”),有△EGC ∽△DFE ,易得D (-2,7),C (1,1).又由对称可知DE =DA =6,EC =CA =3,△EGC 与△DFE 的相似比为1∶2,设CG =x ,则EF =2x ,EG =6-2x ,∴DF =12-4x ,故12-4x =3+x ,有x =95.故E (145,175).归纳若知道直角三角形的两直角边的长度(比值),可通过两个锐角顶点作过直角顶点直线的垂线段构造K 字型全等或相似. 结论应用1.如图,在Rt △AOB 中,O 为坐标原点,∠AOB =90°,OA :OB =1:2,如果点A 在反比例函数()10y x x=>的图象上运动,那么点B 在函数________(填函数解析式)的图象上运动.【答案】4y x=-提示:分别过点A ,B 作y 轴的垂线于点C ,D ,由“K 字模型”知△OCA ∽△BDO ,且知相似比为1:2.设A (m ,1m ),AC =m ,OC =1m ,则OD =2m ,BD =2m ,∴B (2m,-2m ),故点B 在4y x =-上.B变式1:如图,在Rt △AOB 中,O 为坐标原点,∠AOB =90°,∠B =30°,如果点A 在反比例函数()10y x x=>的图象上运动,那么点B 在函数________(填函数解析式)的图象上运动.变式1图【答案】3y x =-提示:构造“K 字型”,其中OA OB =.变式2:已知A 是反比例函数3y x=的图象在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为边作等边△ABC ,点C 在第四象限.已知点C 的位置始终在一函数图象上运动,则这个函数解析式为________.变式2图【答案】9y x=-提示:由反比例函数图象的中心对称性可知,OA =OB ,故连接OC ,后续步骤同变式1. 变式3:已知△ABC 为等边三角形,点A 与点D 的坐标分别是A (4,0),D (10,0). (1)如图①,当点C 与点O 重合时,求直线BD 的解析式;图①【答案】(1)42y x =-(2)如图②,点C 从点O 沿y 轴向下移动,当以点B 为圆心,AB 为半径的⊙B 与y 轴相切(切点为C )时,求点B 的坐标;图②【答案】B (8,-)(3)如图③,点C 从点O 沿y 轴向下移动,当点C 的坐标为C (0,-)时,求∠ODB 的正切值.图③【答案】法1:在x 轴上找点E ,F 使∠OEC =∠AFB=60°(构造“一线三等角),如图①所示,显然有△AEC ≌△BF A (AAS ).在Rt △OEC 中,OC =OEC =60°,则OE =2,∴AE =6.于是由全等得BF =AE =6.过点B 作BG ⊥x 轴于点G ,在Rt △FGB 中,∠GFB =60°,BF =6,∴FG =3,BG=DG =5,故tan ∠ODB图③【答案】法2:过点B 作BE ⊥AC 于点E ,过点E作直线FG ⊥x 轴于点F ,过点B 作BG ⊥FG 于点G ,如图②所示(构造“K 字模型”),有△AFE ∽△EGB,且AE BE =.由“三线合一”知E 为AC 的中点,则EF 为△AOC 的中位线,∴AF =2,EF EG=BG =3,则B (5,-,易求tan ∠ODB图③归纳只要知道等边三角形两个点的坐标,经过定边的中点构造.“K 字型”.变式4:如图,在等腰Rt △OAB 中,∠OAB =90°,顶点O 为坐标原点,顶点A ,B 在某反比例函数的图象上,点A 的横坐标为2,则OAB S =△________.变式4图【答案】5A 作MN ∥y 轴交x 轴于点N ,过点B 作BM ⊥MN 于点M (构造“K 字模型”),有△BMA ≌△ANO (AAS ).设A (2,m )(m >0),则可得B (2-m ,2+m ).根据“双曲线上的点横、纵坐标的积相等”,得(2-m )(2+m )=2m ,解得m 1,∴()22114522ABC S OA m ==+=-△变式4图2.如图,直线123l l l ∥∥,且1l 与2l 的距离为1,2l 与3l 的距离为3.把一块含有45°的直角三角板按图所示放置,顶点A ,B,C 恰好分别落在三条直线上,AC 与直线2l 交于点D ,则线段BD =________.【答案】2543.如图,点P 是正方形ABCD 的BC 边上的动点,以AP 为斜边在正方形内部作一等腰 Rt △APQ ,∠AQP=90°;AQ=PQ. (1)求∠ADQ 的度数;(2)若正方形边长为4,BP=1,求DQ 的长.P答案:法1:(1)过点Q 作EF//AB 分别交AD ,BC 于点E ,F ,如图所示(构造“K 字模型”),显然△AEQ ≌△QFP (AAS ),∴AE=QF.又AD=EF ,则AD-AE=EF-QF ,即ED=EQ ,∴∠ADQ=45°. (2)设DE=EQ=FP=m,又BP=1, 则CF=3-m=DE=m ,∴32m =,则2. 法2:(1)连接AC ,如图②所示,AQ AD AP AC ==, 则△AQD△APC ,∠ADQ=∠ACB=45°.(2)由△AQD△APC 可得DQ PC =PC=3,则DQ=2. 图①FEBP 图②AP变式:如图,以ABCD 的CD 边为斜边向内作等腰Rt △CDE ,使AD=DE=CE ,∠DEC=90°,且点E 在平行四边形内部.连接AE ,BE ,则∠AEB 的度数是____________.B答案:135°提示:过点E作FG⊥AD交AD,BC于点G,F,利用“等腰三角形腰上的高与底的夹角等于顶角的一半”,得∠1=12∠3,∠2=12∠4.而∠3+∠4=180°-2×45°=90°,∴∠1+∠2=45°,故∠AEB=135°.4.如图,在平面直角坐标系中,直线34y x b=-+分别与x轴,y轴交于点A,B,且点A的坐标为(8,0),四边形ABCD是正方形.备用图(1)填空:b=_________;(2)求点D的坐标;(3)M是线段AB上的一个动点(点A,B除外),试探索在x轴上方是否存在另一个点N,使得以0,B,M,N 为顶点的四边形是菱形.若不存在,请说明理由;若存在,请求出点N的坐标.答案:(1)6. (2)D(14,8). (3)存在,点N的坐标为144192(,)2525或(-4,3).变式:如图,在平面直角坐标系中,矩形OABC的顶点A,B在双曲线kyx=(x>0)上,BC与x转交于点D.若点A的坐标为(2,4),求点D的坐标.答案:过点A作EF//x轴交y轴于点E,过点B作BF//y轴交EF于点F(构造“K字模型”),显然有△AEO △BFA ,设B (m ,8m ),则AF=m-2,BF=4-8m, ∴AE BF OE AF =,即m-2=8-16m, ∴m=8,则点B (8,1), 又BC//OA ,则BC OA k k ==2, ∴BC l :y=2x-15,与x 轴的交点D (152,0). 五、双子型 1.全等双子型(1)如图,△ABC 和△CED 均为等边三角形,C 为公共点,那么,在下图中,我们能得到哪些结论呢?BB常见结论:三角形全等:___________;线段相等:______________;角的结论:__________________. (2)稍微变一下形,如下图,△ABC 和△CED 均为等腰直角三角形,C 为公共点.B B常见结论:三角形全等:___________;线段相等:______________;角的结论:__________________. (3)再稍微变一下形,我们把两个等腰直角三角形换成两个正方形,你还能找出结论吗?EFEF常见结论:三角形全等:___________;线段相等:______________;角的结论:__________________.(4)我们拓展到一般情况,如下图,△ABC 和△ADE 均为等腰三角形,C 为公共点,且满足∠BAC=∠DAE.BD常见结论:三角形全等:___________;线段相等:______________;角的结论:__________________. 答案:(1)结论:△BCE ≌△ACD (SAS );BE=AD ;∠AFB=60°(可补充FC 平分∠BFD ); (2)结论:△BCE ≌△ACD (SAS );BE=AD ;∠AFB=90°(可补充FC 平分∠BFD ); (3)结论:△BCG ≌△DCE (SAS );BE=DG ;∠BHE=90°(可补充HC 平分∠BHE ); (4)结论:△BAD ≌△CAE (SAS );BD=CE ;∠BFC=∠BAC (可补充FA 平分∠BFE ). 2.相似双子型上面的结论都是全等,既然全等是特殊的相似,那相似肯定也是有的!如图,△ABC 和△CED 均为直角三角形,C 为公共点,且满足∠BAC=∠CDE.BB仿照上面的结论,有:三角形相似:______;相似比为_______;线段关系:_______;角的结论:____________. (若命题人将上面的图形补成矩形,可要慧眼识珠哦!) 答案:结论:△BCE△ACD ;BC AC (或tanA );BE BCAD AC;∠AFB=90°归纳 在双子型的公共点除必存在旋转类的全等或相似外,同时极易出现“八字形”.练一练1.已知:如图①,在△AOB 和△COD 中,OA = OB ,OC =OD ,∠AOB=∠COD = 50°. (1)求证:①AC = BD ;②∠APB=50°;(2)如图②,在△AOB 和△COD 中,OA=OB ,OC=OD ,∠AOB=∠COD=a ,则AC 与BD 间的数量关系为_________,∠APB 的大小为___________.图①DAQ图②AB答案:(1)略. (2)AC=BD ,∠APB=a.2.(1)只需证△BAM ≌△CAN .(2)仍然成立(还可发现∠MAC =∠CNM ) 【构造双子型】1.6提示:以C 为顶点,CD 为边向右下方作等边△CDE ﹙构造“双子型”﹚,连接AE,有△BCD ≌△ACE﹙SAS ﹚,AE =BD=7.5,在Rt △ADE 中,AD =4.5,AE =7.5,由勾股定理得DE =6,即CD =6.2.13提示:以A 为顶点,AB 为腰向左上方作等腰Rt △ABE ﹙构造“双子型”﹚,连接CE ,有△ABD ≌△AEC ﹙SAS ﹚在Rt △EBC 中,EB =5,BC =12, 由勾股定理得CE =13,即BD =CE =13.变式1:10提示:以A 为顶点,AB 为腰作等腰△AEB ,且使∠EAB =120°﹙构造“双子型”﹚,连接CE,有△BAD ≌△EAC﹙SAS ﹚,在Rt △EBC 中,EB =6,BC =8,由勾股定理得CE =10,即BD =10.ED C B AE D AB CEDBCA变式2:2提示:以P 为顶点,PB 为边长向右下方作等边△PBE ,连接CE ,有△BP A ≌△BEC ﹙SAS ﹚,∠BEC =∠A PB=150°,又∠BEP =∠BPE =60°,在Rt △PEC 中,PE =1,∠EPC=60°,得CP =2.提示:以A 为顶点,AD 为腰作等腰Rt △ADE ﹙构造“双子型”﹚,连接CE,有△BAD ≌△CAE ﹙SAS ﹚在Rt △EDC 中,EDCD =2,由勾股定理得CE故BD4.4≤AC ≤6 提示:以B 为顶点,OB 为边向上方作等腰Rt △OBP ﹙构造“双子型”﹚,连接CP ,OM,有△BOM ≌△BPC ﹙SAS ﹚,PC =OM =1,则点C 在以P 为圆心,1为半径的圆上,这样就转1C ,2C 两化为“圆外一点到圆上的最值问题”,作射线AP ,交⊙P 于点,A 1C =4,A 2C =6.故4≤AC ≤6.﹙本题亦可以理解为“捆绑旋转”﹚变式1OD ≤3:以O 为顶点,OC 为边向上方作等腰Rt △OEC ︰,则﹙构造“双子型”﹚,连接DE ,OP ,有△OPC ∽△EDC ,且相似比为1DE =则点D 在以E 为圆心,作射线⊙E 于点1D ,2D ,O 1DO 2D=3故OD ≤3﹢变式2:2≤OD ≤4 提示:以OC 为边向上方作等边△OCE ,连接DE,OP.EBAD25.3 提示以O 为顶点,OC 为边向下方作等边△OCE ﹙构造“双子型”﹚,连接EP ,显然有△PCE ≌△DCO ﹙SAS ﹚,故OD =EP ,这样OD 的最值转化到EP 的最值,E 为定点,点P 在⊙O 上,根据“圆内一点到圆上各点最值问题”可以得解,作直线OE 交⊙O 于1P ,2P 两点,则E 1P 为最大值,E 1P =3,E 2P 为最小值, E 2P =1,故OD 的最大值为3,﹙本题还可以问最小值,甚至问OD 的取值范围﹚6.2 提示:以OA 为边向上方等边△OAD ﹙构造“双子型”﹚,连接BD,显然有△ADB ≌△AOC ﹙SAS ﹚,则OC =BD ,D 为定点,动点B 在y 轴上,根据“点到直线的距离,垂线段最短”,可知当DE ⊥y 轴时﹙即E,B 重合时﹚,DB 最短,此时DB =2,故OC 的最小值为2.7.提示:以OA 为腰向上作等腰Rt △AOD ﹙构造“双子型”﹚,连接BD ,显然有△AOC ∽△ADB ,∴OC BD =OA AD,则OCD 为定点,动点B 在直线y =2上运动,根据“点到直线的距离,垂线段最短”,可知当DB ⊥直线y =2时,DB 有最小值2.故OC 的最小值为8.﹙2-以AB 为腰向上作等腰Rt △DAB ,如图①所示﹙构造“双子型”﹚,连接DM ,有△MDB ∽△P AB ,∴2DM DB APAB,则DM则M 在以D为圆心, ,∴maxAM =3minAM 但求点P 的坐标,会比较烦琐,我们看下面的处理方法.以AB 为底向下作等腰Rt △ABN ,连接NP ,如图②所示,有△MAB ∽△PNB ,∴AM .N 为定点,P 在以A 为圆心,2为半径的圆上,当N,A,P 三点共线时,NP 最大,在Rt △ADP 中,AP =2,∠P AD =45°,∴AD=DP 故点P 坐标为﹙2-DM'O AMPB DNBPMAO六、十字架型【正方形内十字架型】1.△BAF≌△ADE﹙SAS﹚;AE=BF2.在正方形ABCD中,E、F、G、H分别为AB、CD、AD、BC边上的点. 若EF⊥GH,上述结论是否仍然成立?解:仍然成立提示:过点G作GN⊥BC于点N,过点F作FM⊥AB于点M,再证△GNH≌△FME即可.思路正方形中“十字架的顶点分别在四条边上”→“垂直”可以利用全等推导出十字架“相等”.3.如图,将边长为4的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边上,求折痕FG的长.解:连结AE. FG为折痕,AE为对称点的连线,则AE⊥FG. 又四边形ABCD为正方形,根据“正方形内十字架型”可得FG=AE=52.【矩形内十字架型】1.如图,在矩形ABCD中,AB=m,AD=n,在AD边上有一点E. 若CE⊥BD,则CE和BD之间有什么数量关系?解:可证△CDE ∽△BCD ,∴nmBC CD BD CE ==,即CE ,BD 之比等于矩形邻边之比.2. 如图所示为一般情况,在矩形ABCD 中,E 、F 、G 、H 分别为AD ,BC ,AB ,CD 边上的点,当EF ⊥GH ,上诉结论是否仍然成立?解:仍然成立,BCCDGH EF =.思路 矩形中“十字架的顶点分别在四条边上”→“垂直”可以利用相似推导出十字架之比和邻边“成比例”. 3. (秒算)如图,把边长为AB=6,BC=8的矩形ABCD 对折,使点A 和点C 重合,求折痕EF 的长.解:连结AC ,BC CD AC EF =,∴8610=EF ,故EF=215.探究证明某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两相邻边的数量关系进行探究,提出下列问题,请你给出证明.如图,在矩形ABCD 中,EF ⊥GH ,EF 分别角AB ,CD 于点E ,F ,GH 分别交AD ,BC 于点G ,H. 求证:ABADGH EF =.结论应用如图,在满足上题的条件下,又AM ⊥BN ,点M 、N 分别在BC ,CD 边上,若1511=GH EF ,则=AMBN.答案:1511联系拓展如图,在四边形ABCD 中,∠ABC=90°,AB=AD=10,BC=CD=5,AM ⊥DN ,点M ,N 分别在BC ,AB 边上,求AMDN 的值.解:可证△ADC≌△ABC ,∴∠ADC=∠ABC=90°. 过点D 作EF ∥AB ,过点A 作AF ⊥EF 于点F ,延长BC 交EF 于点E ,如图(构造“K 字模型”),又有△DEC ∽△AFD ,且相似比为1:2.设CE=x ,则DF=x 2,∴DE=x 210-,∴AF=x 420-=BE=x +5,∴3=x ,则BE=8. 根据“矩形内十字架型”可得54==AB BE AM DN .【直角三角形内十字架型】直角三角形可以看成是连接矩形对角线后分成的图形,所以矩形内的结论可沿用至直角三角形内. 1.如图,在Rt 三角形ABC 中,∠ABC =90°,BA =BC ,D 是BC 边上的中点。

线段(双中点)、角(双角平分线)模型线段(双中点)模型讲解【口诀】字母去重,线段留半 【结论1】已知点B 在线段AC 上,AB=8cm ,AC=18cm.(1)P 、Q 分别是AB 、BC 的中点,则PQ 为_________cm. (2) P 、Q 分别是AC 、BC 的中点,则PQ 为_________cm. (3) P 、Q 分别是AB 、AC 的中点,则PQ 为_________cm. 已知点B 在直线AC 上,AB=8cm ,AC=18cm.(1)P 、Q 分别是AB 、BC 的中点,则PQ 为_________cm. (2) P 、Q 分别是AC 、BC 的中点,则PQ 为_________cm. (3) P 、Q 分别是AB 、AC 的中点,则PQ 为_________cm. 【答案】9;4;5;9;4;5或13【结论2】已知点C 在线段AB 上,点M ,N 分别是AC ,BC 的中点,则MN= 12AB.【证明】∵M ,N 分别是AC ,BC 的中点, ∴CM= 12AC ,CN= 12BC,∴MN=CM+CN= 12AC+ 12BC= 12(AC+BC)= 12AB.【结论3】已知点C 是线段AB 延长线上一点,点M ,N 分别是AC ,BC 的中点,则MN= 12AB.【证明】∵M.N 分别是AC ,BC 的中点, ∴MC= 12AC ,NC= 12BC ,∴MN=MC-NC= 12AC- 12BC= 12(AC-BC)= 12AB.拓展已知点C 是线段BA 延长线上一点,点M ,N 分别是AC.BC 的中点,则MN= 12AB.无论线段之间的和差关系怎样变,MN 的长度只与AB 有美,即MN= 12AB.典型例题典例1如图,点C 是线段AB 上一点,AC <CB ,M ,N 分别是AB 和CB 的中点,AC=8,NB=5,则线段MN=___________.典例2如图,已知点A ,B ,C 在同一直线上,M ,N 分别是AC ,BC 的中点.(1)若AB=20,BC=8.求MN的长;(2)若AB= a,BC=8.求MN的长;(3)若AB= a,BC= b.求MN的长;(4)从(1) (2) (3)的结果中能得到什么结论?典例3如图,线段AB=10cm,BC=3cm,点D,E分别为AC和AB的中点,则DE的长是_________.初露锋芒1.已知线段AB=10cm,点C是直线AB上一点,BC=4 cm,若M是AC 的中点,N是BC的中点,则线段MN的长度是( ).A.7 cmB.3 cmC.5 cmD.7 cm或3 cm2.如图,已知A,B.C三点在同一直线上,AB=24.BC= 3AB,E是AC8的中点,D是AB的中点,则DE的长度是___________.3. 如果A、B、C三点在同一直线上,且线段AB=6cm,BC=4cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( ).A.5cmB.1cmC.5或1cmD.无法确定4. 已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC 的中点,N是BC的中点,则线段MN的长度是( )A.7cmB.3cmC.7cm或3cmD.5cm感受中考1.(2018贵州铜仁中考模拟)C为线段AB上任意一点,D、E分别是AC,CB的中点,若AB=10cm.则DE的长是( ).A.2 cmB.3 cmC.4 cmD.5 cm2.(2018湖南邵阳中考模拟)已知点C为线段AB上任一点,AC=8 cm,CB=6cm,M,N分别是AC,BC的中点.(1)求线段MN的长;(2)点C为线段AB上任一点,满足AC+CB= a cm,点M,N分别是AC,BC的中点,你能猜想MN的长度吗?并说明理由.(3)点C在线段AB的延长线上,满足AC-BC=b cm,M,N分别是AC,BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.(4)你能用一句简洁的话,描述你发现的结论吗?3.如图,已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)BP=________,点P表示的数________ (分别用含t的代数式表示);(2)点P运动多少秒时,PB=2PA.(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.参考答案典例1 【答案】4【解析】∵M ,N 分别是AB 和CB 的中点, ∴根据线段(双中点)的结论,有MN= 12AC.则MN=4. 典例2【答案】从(1)(2)(3)的结果中能得到:线段MN 始终等于线段AB 的一半,与C 点的位置无关. 【解析】(1)∵AB=20,BC=8. ∴AC=AB+BC=28.∵点A ,B ,C 在同一直线上,M ,N 分别是AC ,BC 的中点. ∴MC= 12AC.NC= 12BC.∴MN=MC-NC= 12(AC-BC)= 12AB=10.(2)根据(1)得MN= 12 (AC-BC)= 12AB= 12a .(3)根据(1)得MN= 12(AC-BC)= 12AB= 12a .(4)从(1)(2)(3)的结果中能得到:线段MN 始终等于线段 AB 的一半,与C 点的位置无关.典例3 【答案】1.5【解析】∵AB=10cm ,BC=3cm ,(已知) ∴AC=AB-BC=7cm.∵点D 为AC 中点,点E 为AB 的中点,(已知) ∴AD= 12AC,AE= 12AB.(线段中点定义)∴AD=3.5cm,AE=5cm. ∴DE=AE-AD=1.5cm. 故答案为:1.5.初露锋芒1.【答案】C.【解析】当点C 在线段AB 上时,如图.∵M ,N 分别是AC ,BC 的中点,∴根据线段(双中点)的结论,可知MN= 12AB=5 cm.当点C 在线段AB 的延长线上时,如图.∵M ,N 分别是AC ,BC 的中点,∴根据线段(双中点)的结论,可知MN= 12AB=5 cm.综上所述,MN 的长为5cm. 故选C.2. 【答案】92.【解析】∵AB=24,BC= 38AB ,∴BC=9.∵E 是AC 的中点,D 是AB 的中点,∴根据线段(双中点)的结论,可知DE= 12BC= 92.3. 【答案】C【解析】如图1,当点B 在线段AC 上时,∵AB=6cm ,BC=4cm ,M ,N 分别为AB ,BC 的中点, ∴MB= 12AB = 3cm,BN = 12BC = 2cm,∴MN=MB+NB=5cm,如图2,当点C 在线段AB 上时,∵AB=6cm ,BC=4cm ,M ,N 分别为AB ,BC 的中点, ∴MB= 12AB = 3cm ,BN= 12BC=2cm,∴MN=MB-NB=1cm 。

初中数学常用几何模型及构造方法大全全等变换平移:平行等线段〔平行四边形〕对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型角分线模型*说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等.两边进行边或者角的等量代换,产生联系.垂直也可以做为轴进行对称全等.对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称〔翻折〕,翻折成正方形或者等腰直角三角形、等边三角形、对称全等.旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等.自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中央对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容.通过“8〃字模型可以证实.模型变形aD另外是等腰直角三角形与正方形的混用.当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等.中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证实另外两个顶点与中点所成图形为等腰直角三角形.证实方法是倍长所要证等腰直角三角形的一直角边,转化成要证实的等腰直角三角形和的等腰直角三角形〔或者正方形〕公旋转顶点,通过证实旋转全等三角形证实倍长后的大三角形为等腰直角三角形从而得证.中点模型他长一边构通中也或向造三管合一向造斜边中转隹中点梅淮中位位几何最值模型对称最值〔两点间线段最短〕线段和差模型轴对称模型对称最值〔点到直线垂线段最短〕说明:通过对称进行等量代换,转换成两点间距离及点到直线距离. 旋转最值〔共线有最值〕说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的 同侧,异侧两线段之和最苗模型同趴 异恻两线段之笔以小模T ;三线段之和过桥模蛰最短模型四边出周长三珀形周长 最小模型最小模型和为最大值,定长线段的差为最小值.剪拼模型三角形今四边形四边形个四边形nq\ 牙图11说明:剪拼主要是通过中点的180度旋转及平移改变图形的形状. 矩形今正方形说明:通过射影定理找到正方形的边长,通过平移与旋转完成形状改变正方形♦等腰直角三角形今正方形面积等分旋转相似模型说明:两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似.推广:两个任意相似三角形旋转成一定角度,成旋转相似.第三边所成夹角符合旋转“8〃字的规律.D相似模型说明:注意边和角的对应,相等线段或者相等比值在证实相似中起到通过等量代换来构造相似三角形的作用.说明:〔1〕三垂直到一线三等角的演变,三等角以30度、45度、60度形式出现的居多.〔2〕内外角平分线定理到射影定理的演变,注意之间的相同与不同之处.另外,相似、射影定理、相交弦定理〔可以推广到圆幂定理〕之间的比值可以转换成乘积,通过等线段、等比值、等乘积进行代换, 进行证实得到需要的结论.说明:相似证实中最常用的辅助线是做平行,根据题目的条件或者结论的比值来做相应的平行线.。

初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
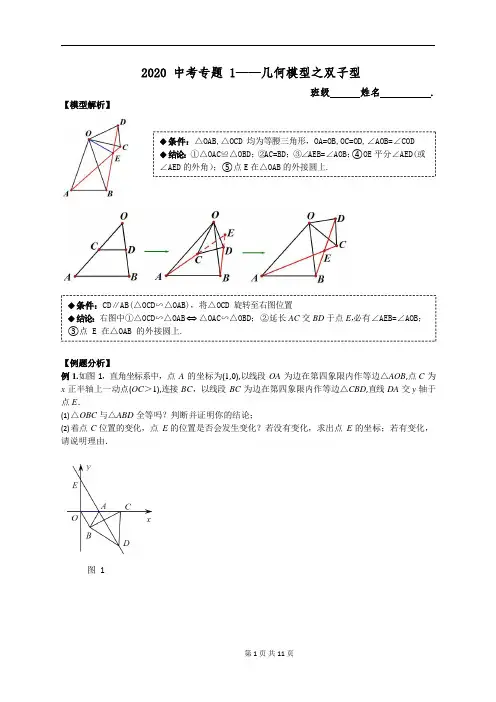
◆条件:CD∥AB(△OCD∽△OAB),将△OCD 旋转至右图位置◆结论:右图中①△OCD∽△OAB △OAC∽△OBD;②延长AC交BD于点E,必有∠AEB=∠AOB;③点 E 在△OAB 的外接圆上.【模型解析】2020 中考专题 1——几何模型之双子型班级姓名.【例题分析】例1.如图1,直角坐标系中,点A 的坐标为(1,0),以线段OA 为边在第四象限内作等边△AOB,点C 为x 正半轴上一动点(OC>1),连接BC,以线段BC 为边在第四象限内作等边△CBD,直线DA 交y 轴于点E.(1)△OBC 与△ABD 全等吗?判断并证明你的结论;(2)着点C 位置的变化,点E 的位置是否会发生变化?若没有变化,求出点E 的坐标;若有变化,请说明理由.图 1◆条件:△OAB,△OCD 均为等腰三角形,OA=OB,OC=OD,∠AOB=∠COD◆结论:①△OAC≌△OBD;②AC=BD;③∠AEB=∠AOB;④OE平分∠AED(或∠AED的外角);⑤点E在△OAB的外接圆上.3例2.如图 2-1,在Rt△ABC 中,∠B=90°,cosC=5,点6D、E 分别是边BC、AC 的中点,连接DE,AE将△EDC 绕点C 按顺时针方向旋转,记旋转角为θ.当0°≤θ<360°时,仅就图2-2 的情况给出证明.图2-1 图2-2的大小有无变化?请BD例3.如图3 所示,在四边形ABCD 中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD 的长为.图3 图4例4.如图4,在△ABC 中,∠ABC=60°,AB=2 ,BC=8,以AC 为腰,点A 为顶点作等腰△ACD,且∠DAC=120°,则BD 的长为.【巩固练习】1.如图1,△ABC 和△ADE 都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O 为AC 中点,若点D 在直线BC 上运动,连接OE,则在点D 运动过程中,线段OE 的最小值是为()A1B.C.1.2 2图1 图22.如图2,△ABC 为等边三角形,AB=2,点D 为BC 边上的动点,连接AD,以AD 为一边向右作等边△ADE,连接CE. (1)在点D 从点B 运动到点C 的过程中,点E 运动的路径长为;(2)在点D 的运动过程中,是否存在∠DEC=60°,若存在,求出BD 的长,若不存在,请说明理由.(3)取AC 中点P,连接PE,在点D 的运动过程中,求PE 的最小值.2D. 23.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图3-1,当点C1在线段C A的延长线上时,求∠CC1A1的度数;(2)如图3-2,连接AA1,CC1.若△A1BA1的面积为4,求△CBC1的面积;图3-1 图3-24.【提出问题】(1)如图4-1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM 为边作等边△AMN,连结CN.求证:BM=CN.【类比探究】(2)如图4-2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN 还成立吗?请说明理由.【拓展延伸】(3)如图4-3,在等腰△ABC 中,BA=BC,AB=6,AC=4,点M 是BC 上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究BM与CN的数量关系,并说明理由.图4-1 图4-2 图4-35.如图5,正方形ABCD、BGFE 边长分别为2、1,正方形BGFE 绕点B 旋转,直线AE、GC 相交于点H.(1)在正方形BGFE绕点B旋转过程中,∠AHC的大小是否始终为90°,请说明理由;(2)连接DH、BH,在正方形BGFE 绕点B 旋转过程中,求DH 的最大值;图5 备用图6.如图6-1,已知点A(0,-3)和x 轴上的动点C(m,0),△AOB 和△BCD 都是等边三角形.(1)在C 点运动的过程中,始终有两点的距离等于OC 的长度,请将它找出来,并说明理由.(2)如图6-2,将△BCD 沿CD 翻折得△ECD,当点C 在x 轴上运动时,设点E(x,y),请你用m 来表示点E 的坐标并求出点E 运动时所在图象的解析式.(3)在C 点运动的过程中,当m 时,直接写出△ABD 是等腰三角形时E 点的坐标.图1 图237.【问题探究】(1)如图7-1,锐角△ABC 中分别以AB、AC 为边向外作等腰△ABE 和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD 与CE 的大小关系,并说明理由.【深入探究】(2)如图7-2,四边形ABCD 中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45°,求BD 的长.(3)如图7-3,在(2)的条件下,当△ACD 在线段AC 的左侧时,求BD 的长.图7-1 图7-2 图7-38.(1)如图8-1,已知△ABC,以AB、AC 为边分别向△ABC 外作等边△ABD 和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;(2)如图8-2,利用(1)中的方法解决如下问题:在四边形ABCD 中,AD=3,BD=2,∠ABC=∠ACB=∠ADB=45°,求BD 的长;(3)如图8-3,四边形ABCD中,∠BAC=90°,∠ADB=∠ABC=α,tanα=4,B D=5,AD=12,求BD 3的长.图8-1 图8-2 图8-32020 中考专题1——几何模型之双子型参考答案例1.解:①全等.理由:∵△AOB 和△CBD 是等边三角形,∴OB=AB,∠OBA=∠OAB=60°,BC=BD,∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,在△OBC 和△ABD 中,∵,∴△OBC≌△ABD(SAS).②不变.理由:∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,又∵∠OAB=60°,∴∠OAE=180°﹣∠OAB﹣∠BAD=60°,∴Rt△OEA 中,AE=2OA=2,∴OE=,∴点E的位置不会发生变化,E的坐标为E(0,).例2.当0°≤α<360°时,的大小没有变化,∵∠ECD=∠ACB,∴∠ECA=∠DCB,又∵==,∴△ECA∽△DCB,∴==;例3.解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,在△BAD 与△CAD′中,,∴△BAD≌△CAD′(SAS),∴BD=CD′,∠DAD′=90°,由勾股定理得DD′==3 ,∠D′DA+∠ADC=90°,由勾股定理得CD′==,∴BD=CD′=.故答案为:.例4.解:以A 为旋转中心,把△BAC 逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE 于P,则∠BAE=120°,AB=AE,∴∠ABE=∠AEB=30°,∴BP=AB•cos∠ABP=3,∠AEB=90°,∴BE=2BP=6,在Rt△BED 中,BD==10,故答案为:10.【巩固训练】1. 解:设 Q 是 AB 的中点,连接 DQ ,∵∠BAC =∠DAE =90°,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,即∠BAD =∠CAE , ∵AB =AC =2,O 为 AC 中点,∴AQ =AO , 在△AQD 和△AOE 中,,∴△AQD ≌△AOE (SAS ),∴QD =OE ,∵点 D 在直线 BC 上运动,∴当 QD ⊥BC 时,QD 最小,∵△ABC 是等腰直角三角形,∴∠B =45°, ∵QD ⊥BC ,∴△QBD 是等腰直角三角形,∴QD =QB ,∵QB = AB =1,∴QD =,∴线段 OE 的最小值是为.故选:B .2. 解:(1)△ABD ≌△ACE 可得 BD =CE ,E 的运动路径的长即 D 的运动路径长,BC =2.(2) ∠DEC =60°相当于∠AEC =∠ADB =120°,即∠EDC =0°,此时点 D 与点 B 重合.因此不存在.(3) ∠ACE =60°,当 PE ⊥CE 时取最小值.PE =PC cos 60°=1.23. 解:(1)由旋转的性质可得:∠A 1C 1B =∠ACB =45°,BC =BC 1, ∴∠CC 1B =∠C 1CB =45°,∴∠CC 1A 1=∠CC 1B +∠A 1C 1B =45°+45°=90°. (2)∵△ABC ≌△A 1BC 1,∴BA =BA 1,BC =BC 1,∠ABC =∠A 1BC 1,∴,∠ABC +∠ABC 1=∠A 1BC 1+∠ABC 1,∴∠ABA 1=∠CBC 1,∴△ABA 1∽△CBC 1.∴,∵S △ABA 1=4,∴S △CBC 1= ;4.(1)证明:∵△ABC 、△AMN 是等边三角形, ∴AB =AC ,AM =AN ,∠BAC =∠MAN =60°, ∴∠BAM =∠CAN ,∵在△BAM 和△CAN 中,∴△BAM ≌△CAN (SAS ), ∴∠ABC =∠ACN .(2) 解:结论∠ABC =∠ACN 仍成立;理由如下:∵△ABC 、△AMN 是等边三角形,∴AB =AC ,AM =AN ,∠BAC =∠MAN =60°,∴∠BAM =∠CAN ,∵在△BAM 和△CAN 中,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.(3)解:∠ABC=∠ACN;理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴=,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.5.解:(1)是,理由如下:如图,由旋转知,∠ABE=CBG,在正方形ABCD,BGFE 中,AB=BC,BE=BG,∠ADC=∠BCD=∠BAD=∠ABC=90°,∴△ABE≌△CBG,∴∠BAE=∠BCG,记AH 与BC 的交点为点P,∵∠APB=∠CPH,∠ABC+∠BAE+∠APB=180°∠AHC+∠BCG+∠CPH=180°,∴∠AHC=∠ABC=90°,(2)DH≤DE+EG=BD=2 26.解:(1)连接AD,如图1所示.A、D 两点间的距离始终等于OC 的长度.理由如下:∵△AOB 和△BCD 都是等边三角形,∴AB=OB,BD=BC,∠ABO=∠CBD=60°,∵∠ABD=∠ABO+∠OBD,∠OBC=∠OBD+∠DBC,∴∠ABD=∠OBC.在△ABD 和△OBC 中,有,∴△ABD≌△OBC(SAS),∴AD=OC.(2)过D 作DF⊥y 轴于F,连接BE,如图2 所示.由(1)可知△ABD≌△OBC,∴AD=OC=m,∠DAF=∠BAO﹣∠BAD=60°﹣(90°﹣60°)=30°∴DF=AD•sin∠DAF=m,AF=AD•cos∠DAF=m,∵A(0,﹣3),∴D(m,m﹣3).∵将△BCD 沿CD 翻折得△ECD 且△BCD 是等边三角形,∴四边形BCED 是菱形,∴BE、CD 互相平分.∵△AOB是等边三角形,且点O(0,0),点A(0,﹣3),∴点B(,﹣),∴E(m﹣,m﹣).∵m﹣=(m﹣),∴点E在图形y=x上运动.(3)∵点A(0,﹣3),点B(,﹣),点D(m,m﹣3),∴AB=3,AD=m,BD==,△ABD 为等腰三角形分三种情况:①当AB=AD 时,有3=m,此时点E的坐标为(﹣,﹣);②当AB=BD 时,有3=,解得:m=0(舍去),或m=3,此时点E的坐标为(3,3);③当AD=BD 时,有m=,解得:m=(舍去).综上可知:在C 点运动的过程中,当m>时,△ABD是等腰三角形时E点的坐标为(﹣,﹣)或(3,3).7.解:(1)BD=CE.理由是:∵∠BAE=∠CAD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE;(2)如图2,在△ABC 的外部,以A 为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.∵∠ACD=∠ADC=45°,∴AC=AD,∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE.∵AE=AB=7,∴BE==7 ,∠ABE=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC===,∴BD=CE=.(3)如图3,在线段AC 的右侧过点A 作AE⊥AB 于点A,交BC 的延长线于点E,连接BE.∵AE⊥AB,∴∠BAE=90°,又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=7,BE==7 ,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE,∵BC=3,∴BD=CE=(7 ﹣3)cm.8.解:(1)如图1,分别以点A、B为圆心,以AB为半径画弧,交于点D,连接AD、BD,再分别以A、C 为圆心,以AC 为半径画弧,交于点E,连接AE、CE则△ABD、△ACE 就是所求作的等边三角形;证明:如图1,∵△ABD 和△ACE 都是等边三角形,∴AD=AB,AC=AE,∠DAB=∠EAC=60°,∴∠DAC=∠BAE,∴△DAC≌△BAE(SAS),∴BE=CD;(2)如图2,过A 作AE⊥AD,使AD=AE=3,连接DE、CE,由勾股定理得:DE==3 ,∴∠EDA=45°,∵∠ADC=45°,∴∠EDC=∠EDA+∠ADC=90°,∵∠ACB=∠ABC=45°,∴∠CAB=90°,∴∠CAB+∠DAC=∠EAD+∠DAC,即∠EAC=∠DAB,∵AE=AD,AC=AB,∴△DAB≌△EAC(SAS),∴EC=BD,在Rt△DCE 中,EC===,∴BD=EC=;(3)如图3,作直角三角形DAE,使得∠DAE=90°,∠DEA=∠ACB,连接EC,容易得到△DAE∽△BAC,∴,即,∵∠DAE=∠BAC=90°,∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,∴△EAC∽△DAB,∴,在△DCE 中,∠ADC=∠ACB,∠EDA=∠ABC,∴∠EDC=90°,∵,AD=12,∴AE=9,∠DAE=90°,∴DE==15,CE==5 ,由△EAC∽△DAB,∴BD=.第 11 页共 11 页。
初中数学经常使用几何模型及机关办法大全,之五兆芳芳创作掌握它轻松弄定压轴题!几何是初中数学中很是重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省良多时间,这次整理了经常使用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或作边的垂线,形成对称全等.两边进行边或角的等量代换,产生联系.垂直也可以做为轴进行对称全等.对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或等腰直角三角形、等边三角形、对称全等.旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要机关旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等.自旋转模型机关办法:遇60度旋60度,造等边三角形; 遇90度旋90度,造等腰直角;遇等腰旋顶点,造旋转全等; 遇中点旋180度,造中心对称.共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容.通过“8”字模型可以证明.模型变形说明:模型变形主要是两个正多边形或等腰三角形的夹角的变更,另外是等腰直角三角形与正方形的混用.当遇到庞杂图形找不到旋转全等时,先找两个正多边形或等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等.中点旋转:说明:两个正方形、两个等腰直角三角形或一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形.证明办法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证.几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离.旋转最值(共线有最值)说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值.剪拼模型三角形→四边形四边形→四边形说明:剪拼主要是通过中点的180度旋转及平移改动图形的形状.矩形→正方形说明:通过射影定理找到正方形的边长,通过平移与旋转完成形状改动正方形+等腰直角三角形→正方形面积等分旋转相似模型说明:两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似.推广:两个任意相似三角形旋转成一定角度,成旋转相似.第三边所成夹角合适旋转“8”字的纪律.相似模型说明:注意边和角的对应,相等线段或相等比值在证明相似中起到通过等量代换来机关相似三角形的作用.说明:(1)三垂直到一线三等角的演变,三等角以30度、45度、60度形式出现的居多.(2)内外角平分线定理到射影定理的演变,注意之间的相同与不合之处.另外,相似、射影定理、相交弦定理(可以推广到圆幂定理)之间的比值可以转换成乘积,通过等线段、等比值、等乘积进行代换,进行证明得到需要的结论.说明:相似证明中最经常使用的帮助线是做平行,按照题目的条件或结论的比值来做相应的平行线.。
初中数学66个几何模型初中数学有许多有趣的几何模型,下面我将介绍其中的66个。
1. 点:几何中最基本的图形,没有长度和宽度,只有位置。
2. 直线:无穷大延伸的路径,由无数个点组成。
3. 线段:直线的一部分,有特定的长度。
4. 射线:起点固定,向一个方向无限延伸。
5. 角:由两条射线共享起点组成。
6. 直角:角的一种,两条射线相互垂直。
7. 锐角:角的一种,小于90度。
8. 钝角:角的一种,大于90度且小于180度。
9. 平行线:永远不会相交的直线。
10. 垂直线:两条直线相互垂直。
11. 三角形:由三条线段组成的图形。
12. 直角三角形:一条角为直角的三角形。
13. 等腰三角形:两条边长度相等的三角形。
14. 等边三角形:三条边长度都相等的三角形。
15. 直线角:由两条直线相交形成的角。
16. 顶角:两条直线相交时,不在同一边的两角。
17. 锐角三角形:三个角都是锐角的三角形。
18. 钝角三角形:有一个角是钝角的三角形。
19. 平行四边形:有两对平行边的四边形。
20. 矩形:有四个直角的平行四边形。
21. 正方形:既是矩形又是等边四边形的四边形。
22. 平行梯形:有两对平行边的梯形。
23. 圆:平面上由一条弧连结的所有点,到一个固定点的距离相等。
24. 圆心:圆的中心点。
25. 半径:圆心到圆上任意一点的距离。
26. 直径:穿过圆心并且两边端点在圆上的线段。
27. 弦:圆上两点间的线段。
28. 弓形:圆上的一段连续弧。
29. 扇形:由圆心和弧围成的区域。
30. 三角形的面积:三角形内部的空间大小。
31. 四边形的面积:四边形内部的空间大小。
32. 面积:平面图形内部的空间大小。
33. 周长:图形边界的长度。
34. 弧长:圆上弧的长度。
35. 圆周率:常数π,约等于3.14159。
36. 顶点:角的端点。
37. 对角线:多边形内连接两个非相邻顶点的线段。
38. 同位角:两直线被一条截线分割后,位于相应位置的角。
几何图形的基本模型【典型例题】模型一:双子型(手拉手模型)——全等(1)等边三角形条件:ΔOAB,ΔOCD均为等边三角形。
结论:①ΔOAC≌ΔOBD②AC=BD③∠AEB=600④OE平分∠AED⑤点E在ΔOAB的外接圆上(2)等腰直角三角形条件:ΔOAB,ΔOC D均为等腰直角三角形。
结论:①ΔOAC≌ΔOBD②AC=BD③∠AEB=900④OE平分∠AED⑤点E在ΔOAB的外接圆上(3)任意等腰三角形条件:ΔOAB,ΔOCD均为等腰三角形。
结论:①ΔOAC≌ΔOBD②AC=BD③∠AEB=∠A0B④OE平分∠AED(或∠AED的外角)⑤点E在ΔOAB的外接圆上例题:(1)如图①,△ABC中,AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰三角形ABD,ACE,分别取BD,CE,BC的中点M、N、G,连接GM、GN,线段GM与GN数量关系是;位置关系是(2)如图②,把等腰三角形ABC换为一般的锐角三角形,AB﹥AC,其中,其它条件不变,上述结论还成立吗?请说明理由。
(3)如图③,在(2)的基础上,又作了进一步的探究,向△ABC的内侧分别作等腰直角三角形ABD、ACE,其它条件不变,试判断△GMN的形状,并给与证明。
模型二:双子型(手拉手模型)——相似(1)一般情况条件:CD∥AB(ΔOCD∽ΔOAB),将ΔOCD旋转至右图位置结论:右图中①ΔOCD∽ΔOAB⇔ΔOAC∽ΔOBD②延长AC交BD于点E,必有∠AEB=∠AOB ③点E在ΔOAB的外接圆上。
(2)特殊情况条件:CD∥AB(ΔOCD∽ΔOAB),∠AOB=∠COD=900将ΔOCD旋转至右图位置结论:右图中①ΔOCD∽ΔOAB⇔ΔOAC∽ΔOBD②延长AC交BD于点E,必有∠AEB=900(BD ⊥AC)③连接AD,BC,则S ABCD=12AC×BD④OD OC=OB OA=tan∠OCD⑤点E在ΔOAB的外接圆上(A,O,E,B四点共圆)⑥必有AD2+BC2=AB2+CD2例题:以平面上一点O为直角顶点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ABO=∠DCO=300(1)点E、F、M分别是AC、CD、DB的中点,连接FM、EM.1如图1,当点D、C分别在AO、BO的延长线上时,FM EM=2如图2,将图1中△AOB的绕点O沿顺时针方向旋转α角(00<α<600),其他条件不变,判断 的值是否发生变化,并对你的结论进行证明(3)如图3,若B0=33,点N在线段OD上,且NO=2.点P是线段AB上的一个动点,在将ΔOAB绕点0旋转过程中,线段PN长度的最小值为,最大值为。