周期信号的功率证明
- 格式:ppt
- 大小:195.00 KB
- 文档页数:3

信号:我们人类得到的从自己感知中得到消息,并通过大脑分析得出我们要的信息。
而其中消息的传递就需要信号,信号可以是图像、声音还有其他感觉,但是所有信号都是以波的形式在介质中传播。
而机械中的消息则是通过电信号的形式而传播。
最基本的波:正弦波,因为只有一个周期;而理论证明所有的波,都可以用正弦波叠加而成。
我们把这种周期性的波的周期倒数称为频率,这样我们就可以不用在时间上分析波的形态而可以在频率上做研究来分析波的性质。
而不同的信号形式把分解成正弦波的方法不同。
模拟频率f :每秒经历多少个周期,单位Hz ,即1/s ;周期:经过2*pi 需多长时间,单位s 。
模拟角频率Ω:每秒经历多少弧度,单位rad/s ; 数字频率w :每个采样点间隔之间的弧度,单位rad ;周期:经过2*pi 需多少个点,单位1。
关系:Ω=2pi*f ;w = Ω*T = 2π/N 。
(T 为采样间隔时间,N 为一个周期的采样点) 各种函数的关系FS (离散非周期函数)通过Ω = 2πf 将时域信号联系到频域中,它是研究连续周期信号在n Ω角频率处的分量的大小(频谱) FT (连续非周期函数)通过Ω = 2πf 将时域信号联系到频域中,它是研究连续非周期信号在各个角频率处的分量的大小(频谱)的密度函数(因为离散信号是连续信号的取样而成,这导致频谱周期性搬移,所以离散信号的频谱是周 期函数,如果信号时周期信号,因为这相当于我们把一个周期内信号进行搬移,也就是我 们在频域中进行采样,所以频谱是离散的)DFS (离散周期函数) 通过w = Ω*T (T 为采样间隔时间),它是研究离散周期信号,在nw 数字角频率处的分量的大小(频谱)(周期:s ω=2π/T)DTFT (连续周期函数)通过w = Ω*T (T 为采样间隔时间),它是研究离散非周期信号,在各个数字角频率处的分量的大小(频谱)的密度函数(周期:s ω=2π/T)(为了方便计算机运算,引入运算DFT )DFT (离散函数) 通过在DFS 中取主值区间,我们会在下面详细介绍DFT 及FFT 因为这是我们实际处理的工具周期信号的傅里叶级数(FS ) 三角形式: 设 是一个周期为 的波,在一定条件下可以把它写成()f t T ()()01cos 2n n n A f t A n t φ∞==+Ω+∑01cos sin 2n n n A a n t b n t∞==+Ω+Ω∑其中 是 阶谐波, 角频率 (Ω为离散时的角频率形式) 我们称上式右端的级数是由 所确定的傅里叶级数 指数形式:系数Fn 称复傅里叶系数(以证明只要周期信号满足狄里赫利(Dirichlet)条件,就可以分解成傅里叶级数)从上面两个公式,我们可以得出其中的信号的频谱和周期信号的功率(Parseval 等式 , 其中我们也可以得出频率的幅度大小决定信号的功率,这就给我们提供研究信号功率的方法,n F 称为频谱图) 非周期信号的傅里叶变换(FT )为了研究非周期信号的频谱特性,我们引入了傅里叶变换()()d j t F j f t e t +∞-Ω-∞Ω=⎰()1()d 2πj tf t F j e +∞Ω-∞ΩΩ=⎰()F j Ω是频谱密度函数 (Ω为连续时的角频率形式) (从上面公式可以得出,信号的能量谱2()()F j ξΩ=Ω)(上面都是讲的是连续的信号,信号离散也是我们用计算机处理的唯一方法,必须对信号进行采样变成离散的,只要满足采样定理2s m f f >,就能从离散的信号恢复出原来的信号,我们对离散信号的分析和处理也会对原来的连续信号有作用。



傅里叶级数的功率
傅里叶级数是一种将周期函数分解为正弦波和余弦波的无穷级数。
每个正弦和余弦波都有自己的频率和振幅。
功率谱是用来描述信号在每个频率下的能量分布的。
对于周期信号,其功率谱就是傅里叶级数中各个正弦和余弦波的振幅的平方,即功率谱是频率的函数。
对于非周期信号,可以将其视为周期无限大的周期信号,但此时谱线由离散变为连续,各个频率下的能量积分或求和就是信号的总能量,这就是信号的功率谱。
因此,傅里叶级数的功率就是指周期函数的傅里叶级数展开后各个正弦和余弦波的振幅的平方,或者是非周期函数的傅里叶变换后各个频率下的能量积分或求和。


3-3 周期信号的频谱一、 周期信号的频谱一个周期信号)(t f ,只要满足狄里赫利条件,则可分解为一系列谐波分量之和。
其各次谐波分量可以是正弦函数或余弦函数,也可以是指数函数。
不同的周期信号,其展开式组成情况也不尽相同。
在实际工作中,为了表征不同信号的谐波组成情况,时常画出周期信号各次谐波的分布图形,这种图形称为信号的频谱,它是信号频域表示的一种方式。
描述各次谐波振幅与频率关系的图形称为振幅频谱,描述各次谐波相位与频率关系的图形称为相位频谱。
根据周期信号展成傅里叶级数的不同形式又分为单边频谱和双边频谱。
1 单边频谱若周期信号)(t f 的傅里叶级数展开式为式(3-15),即∑ ∞=+Ω+=10)cos()(n n nt n AA t f ϕ (3-24)则对应的振幅频谱n A 和相位频谱n ϕ称为单边频谱。
例3-3 求图3-4所示周期矩形信号)(t f 的单边频谱图。
解 由)(t f 波形可知, )(t f 为偶函数,其傅里叶系数⎰==2/0021)(4T dt t f Ta⎰=Ω=2/0)4/sin(2cos )(4T n n n tdt n t f Ta ππ=n b故∑∑∞=∞=Ω+=Ω+=110cos )4/sin(241cos 2)(n n n tn n n t n a a t f ππ因此410=A ,ππn n A n )4/sin(2=即45.01=A , 32.02≈A , 15.03≈A , 04=A , 09.05≈A , 106.06≈A ┅单边振幅频谱如图3-5所示。
tf(t)图 3 - 4ττττ4 2/ 0 2/ 4--1图 3 - 50.250.450.320.150.090.106ΩΩΩΩΩΩΩ7 6 5 4 3 2 0A n2 双边频谱若周期信号)(t f 的傅里叶级数展开式为式(3-17),即25)-(3 )(∑∞-∞=Ω=n tjn neFt f则nF 与Ωn 所描述的振幅频谱以及n F 的相位n n F θ=arctan 与Ωn 所描述的相位频谱称为双边频谱。


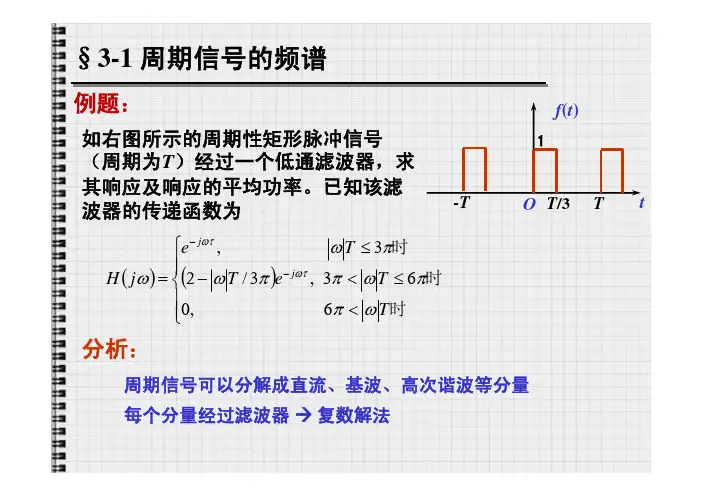
例题:O tf (t )T /31-TT如右图所示的周期性矩形脉冲信号(周期为T )经过一个低通滤波器,求其响应及响应的平均功率。
已知该滤波器的传递函数为()()⎪⎪⎩⎪⎪⎨⎧<≤<-≤=--时时时T T e T T e j H j j ωππωππωπωωωτωτ6,063,3/23,分析:周期信号可以分解成直流、基波、高次谐波等分量每个分量经过滤波器 复数解法解:求傅立叶系数:⎰-=3/001T tjn n dt eTC ωO tf (t )T /31-TT令ω0=2π/T3/0001T t jn eTjn ωω--=3/3sin 31ππjn e n c -⎪⎭⎫ ⎝⎛=3100==C A 2nj n n A eC ϕ=~基波和n 次谐波的复数表示低通滤波器只通过低于3ω0的信号,因此信号中只有直流、基波和二次谐波分量通过。
输出信号中的直流分量为:()3100==ωωj H A解:输出信号中的基波分量的复数表示为:()()τωπωωφπω0013/13sin 32+-=⎪⎭⎫ ⎝⎛=j j e c j H eA 输出信号中的二次谐波分量的复数表示为:()()τωπωωφπω00223/22232sin 94+-=⎪⎭⎫⎝⎛=j j e c j H e A 输出信号的时域表达式为:⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+τωπωπτωπωπ00002322cos 32sin 943cos 3sin 3231t c t c 输出信号的平均功率为:280.02sin 41sin 211222≈⎥⎤⎢⎡⎪⎫⎛+⎥⎤⎢⎡⎪⎫ ⎛+⎪⎫ ⎛=ππc c P out第三章:信号的频谱§3-1 周期信号的频谱§3-2 非周期信号的频谱密度 傅立叶变换与频谱密度信号的频谱分布与带宽基本信号的频谱密度§3-3 频谱分析的基本定理§3-4 采样定理傅立叶变换的引出如何从频域描述一个非周期信号?tf (t )傅立叶级数?——显然不行怎么办?退而求其次,先考虑描述函数在有限区间[a,b)上的一段吧tf a,b (t )a btf T (t )a b考虑有限区间周期扩展再扩展成周期T =b -a 的函数f T (t )f T (t ):周期函数~可以用傅立叶级数表示在区间[a,b)上与f (t ) 相同傅立叶变换的引出tf T (t )a b()(),1100dt et f Tdte tf T C tjn bat jn ba T n ωω--⎰⎰==()()()⎪⎪⎩⎪⎪⎨⎧=-++∈-++=∑∞-∞=b a t b f a f b a t t f t f eC n tjn n或,2)0(0,,2)0(00ω傅立叶级数只在区间(a,b ) 上收敛于f (t ),因此C n 并不是f (t ) 的复频谱如果f T (t ) 满足狄利克雷条件,则可以展开成傅立叶级数:定义:则:ω0=2π/T傅立叶变换的引出进一步,选取对称区间[-T /2,T /2)。

傅里叶变换的基本性质(一)傅里叶变换建立了时间函数和频谱函数之间转换关系。
在实际信号分析中,经常需要对信号的时域和频域之间的对应关系及转换规律有一个清楚而深入的理解。
因此有必要讨论傅里叶变换的基本性质,并说明其应用。
一、线性傅里叶变换是一种线性运算。
若则其中a和b均为常数,它的证明只需根据傅里叶变换的定义即可得出。
例3-6利用傅里叶变换的线性性质求单位阶跃信号的频谱函数。
解因由式(3-55)得二、对称性若则证明因为有将上式中变量换为x,积分结果不变,即再将t用代之,上述关系依然成立,即最后再将x用t代替,则得所以证毕若是一个偶函数,即,相应有,则式(3-56)成为可见,傅里叶变换之间存在着对称关系,即信号波形与信号频谱函数的波形有着互相置换的关系,其幅度之比为常数。
式中的表示频谱函数坐标轴必须正负对调。
例如:例3-7若信号的傅里叶变换为试求。
解将中的换成t,并考虑为的实函数,有该信号的傅里叶变换由式(3-54)可知为根据对称性故再将中的换成t,则得为抽样函数,其波形和频谱如图3-20所示。
三、折叠性若则四、尺度变换性若则证明因a>0,由令,则,代入前式,可得函数表示沿时间轴压缩(或时间尺度扩展) a倍,而则表示沿频率轴扩展(或频率尺度压缩) a倍。
该性质反映了信号的持续时间与其占有频带成反比,信号持续时间压缩的倍数恰好等于占有频带的展宽倍数,反之亦然。
例3-8已知,求频谱函数。
解前面已讨论了的频谱函数,且根据尺度变换性,信号比的时间尺度扩展一倍,即波形压缩了一半,因此其频谱函数两种信号的波形及频谱函数如图3-21所示。
五、时移性若则此性质可根据傅里叶变换定义不难得到证明。
它表明若在时域平移时间,则其频谱函数的振幅并不改变,但其相位却将改变。
例3-9求的频谱函数。
解: 根据前面所讨论的矩形脉冲信号和傅里叶变换的时移性,有六、频移性若则证明证毕频移性说明若信号乘以,相当于信号所分解的每一指数分量都乘以,这就使频谱中的每条谱线都必须平移,亦即整个频谱相应地搬移了位置。
三、功率谱分析字体[大][中][小]周期信号的功率谱为其双边幅值频谱的平方|c n|2;非周期信号的功率谱为其幅值谱密度的平方|X(ω)|2=X(ω)X*(ω)。
随机信号属于时域无限信号,其频率、幅值和相位为随机变量。
因而,采用具有统计特性的功率谱估计进行谱分析(一)自功率谱密度及其估计各态历经随机信号的功率谱密度S x(ω)与自相关函数R x(τ)为傅里叶变换偶对,即为了方便,也可用在非负频率范围内(ω>0)定义的单边功率谱密度G x(ω)代替双边功率谱密度S x(ω),两者之间的关系为自功率谱估计可分为线性估计法与非线性估计法。
前者以快速变换为基础,应用较早,也称为经典谱分析法; 后者是与时序模型结合的一种新方法,又称为现代谱分析方法。
1. 周期图各态历经随机信号的均方值ψx2为信号能量的时域描述。
巴什瓦定理表明,信号能量的时域计算与频域计算相等,即由此定义自功率谱密度及其估计为:式中表12-45 典型信号的自相关、频谱、概率密度(续)X(ω)为测试数据x(t)的傅里叶变换,X(k)为N个数据x(n)的离散傅里叶变换,由FFT 直接求出。
由于X(k)具有周期函数的性质,所以称由此获得的自功率谱估计为周期图。
自相关估计x′(r)的快速傅里叶变换可作为自功率谱估计的另一计算公式以上两种估计都是自功率谱S x(ω)的有偏估计,只是偏差大小不同。
两种估计在时域对数据或对自相关估计进行截断,相当于加窗处理,致使谱估计成为真实功率谱(或称为真功率谱)与窗谱W(ω)的卷积,即Ŝx(ω)=S x(ω)*W(ω)窗谱旁瓣的泄漏效应和卷积的作用使真功率谱的尖峰数值变化,邻近点的数值变大,造成谱估计的模糊与失真以上两种估计的方差较大; 相距2π/N的各点估计值互不相关,故数据点数N越大,这些点的估计值的随机起伏越严重。
为改善谱估计的估计质量,在增大数据点数的同时,采用平均化处理和窗处理方法减小谱估计的方差。