2020年中考数学模拟试题分类汇编--二次函数

知识点20 二次函数在实际生活中的应用1．（2019·山西）北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B 两点,拱高为78米(即最高点O 到AB 的距离为78米),跨径为90米,(即AB ＝90米),以最高点O 为坐标原点,以平行于AB 的直线为x 轴建立平面直角坐标系,则次抛物线型钢拱的函数表达式为( )A.y ＝26675x 2 B.y ＝26675-x 2 C.y ＝131350x 2 D.y ＝131350-x 2第9题图 【答案】B【解析】设二次函数表达式为y ＝ax 2,由题可知,点A 坐标为(－45,－78),代入表达式可得:－78＝a(－45)2,解得a ＝26675-,∴二次函数表达式为y ＝26675-x 2,故选B. 2．（2019年浙江省绍兴市，第22题，12分 ）.有一块形状如图的五边形余料ABCDE ，AB=AE=6，BC=5，∠A=∠B=90°，∠C=135°，∠E ＞90°.要在这块余料中截取一块矩形材料，其中一边在AE 上，并使所截矩形的面积尽可能大.（1）若所截矩形材料的一条边是BC 或AE ，求矩形材料的面积；（2）能否截出比（1）中面积更大的矩形材料？如果能，求出这些矩形材料面积的最大值，如果不能，请说明理由.【解题过程】3．（2019·嘉兴）某农作物的生长率p 与温度t （℃）有如下关系：如图1，当10≤t ≤25时可近似用函数p ＝t ﹣刻画；当25≤t ≤37时可近似用函数p ＝﹣（t ﹣h ）2+0.4刻画．（1）求h 的值．（2）按照经验，该作物提前上市的天数m （天）与生长率p 满足函数关系：生长率p0.2 0.25 0.3 0.35 提前上市的天数m （天）51015①请运用已学的知识，求m 关于p 的函数表达式； ②请用含t 的代数式表示m ．（3）天气寒冷，大棚加温可改变农作物生长速度．在（2）的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此给大棚继续加温，加温后每天成本w （元）与大棚温度t （℃）之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．【解题过程】（1）把（25,0.3）的坐标代入21()0.4160p t h =--+，得h =29或h =21. ∵h >25，∴h =29.（2）①由表格可知m 是p 的一次函数，∴m=100p -20.②当1025t ≤≤时，p=11505t -，∴m=11100()20505t --=2t -40. 当2537t ≤≤时，21(29)0.4160p t =--+.∴m=21100[(29)0.4)]20160t --+-=25(29)208t --+（3）（I ）当2025t ≤≤时，由（20，200），（25，300），得20200w t =-∴增加利润为600m+[200×30-w （30-m ）]= 2406004000t t --. ∴当t=25时，增加利润的最大值为6000元. （II ）当2537t ≤≤时，300w =. 增加利润为600m+[200×30-w （30-m ）]= 25900()(29)150008t ⨯-⨯-+=21125(29)150002t --+ ∴当t=29时，增加利润的最大值为15000元.综上所述，当t=29时，提前上市20天，增加利润的最大值为15000元. 4．（2019山东省青岛市，22，10分）某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y （件）与销售单价x （元）之间满足一次函数关系，其图象如图所示. （1）求该商品每天的销售量y 与销售单价x 之间的函数关系式；（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w （元）最大？最大利润是多少？（3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？ 【解题过程】解：（1）设y 与销售单价x 之间的函数关系式为：y kx b =+， 将点(30,100)、(45,70)代入一次函数表达式得：100307045k b k b =+⎧⎨=+⎩，解得：2160k b =-⎧⎨=⎩，故函数的表达式为：2160y x =-+；（2）由题意得：2(30)(2160)2(55)1250w x x x =--+=--+，20-<Q ，故当55x <时，w 随x 的增大而增大，而3050x 剟， ∴当50x =时，w 由最大值，此时，1200w =，故销售单价定为50元时，该超市每天的利润最大，最大利润1200元； （3）由题意得：(30)(2160)800x x --+…，解得：70x „，∴每天的销售量216020y x =-+…，∴每天的销售量最少应为20件．5．（2019·武汉）某商店销售一种商品，童威经市场调查发现：该商品的周销售量y （件）是售价x （元/件）的一次函数，其售价、周销售量、周销售利润w （元）的三组对应值如下表：注：周销售利润＝周销售量×（售价－进价）（1） ① 求y 关于x 的函数解析式（不要求写出自变量的取值范围）② 该商品进价是_________元/件；当售价是________元/件时，周销售利润最大，最大利润是__________元（2） 由于某种原因，该商品进价提高了m 元/件（m ＞0），物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求m 的值【解题过程】（1）设y 与x 的函数关系式为y ＝kx ＋b ，依题意有，501006080k b k b +=⎧⎨+=⎩，解得，k ＝－2，b ＝200，y与x 的函数关系式是y ＝－2x ＋200；（2）将售价50，周销售量100，周销售利润1000，带入周销售利润＝周销售量×（售价－进价）得到，1000＝100×（50－进价），即进价为40元/件；周销售利润w ＝（x －40）y ＝（x －40）（－2x ＋200）＝－2（x －70）2＋1800，故当售价是70元/件时，周销售利润最大，最大利润是1800元，故答案为40，70，1800；（3）依题意有，w ＝（－2x ＋200）（x －40－m ）＝－2x 2＋（2m ＋280）x －8000－200m ＝221401260180022m x m m +⎛⎫--+-+ ⎪⎝⎭ ∵m ＞0，∴对称轴140=702m x +>， ∵－2＜0，∴抛物线开口向下， ∵x ≤65，∴w 随x 的增大而增大，∴当x ＝65时，w 有最大值（－2×65＋200）（65－40－m ）， ∴（－2×65＋200）（65－40－m ）＝1400， ∴m ＝5．6．（2019·黄冈）某县积极响应市政府加大产业扶贫力度的号召，决定成立草莓产销合作社，负责扶贫对象户种植草莓的技术指导和统一销售，所获利润年底分红.经市场调研发现，草莓销售单价y (万元)与产量x (吨)之间的关系如图所示(0≤x ≤100)，已知草莓的产销投人总成本p (万元)与产量x (吨)之间满足P ＝x ＋1. (1)直接写出草莓销售单价y (万元)与产量x (吨)之间的函数关系式； (2)求该合作社所获利润w (万元)与产量x (吨)之间的函数关系式；(3)为提高农民种植草莓的积极性，合作社决定按0.3万元/吨的标准奖励扶贫对象种植户，为确保合作社所获利润w ＇不低于55万元，产量至少要达到多少吨?【解题过程】7. （2019·衢州市）某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为80间，经市场调查表明，该宾馆每间标准房的价格在170～240元之间（含170元，240元）浮动时，每天入住的房间数（间）与每间标准房的价格x （元）的数据如下表：（1）根据所给数据在坐标系中描出相应的点，并画出图象。

2020年全国各地数学中考试题精选之二次函数一、单选题1.（2020·辽阳模拟）已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）.对于下列命题：①b﹣2a=0；②abc＜0；③4a﹣2b+c＜0；④8a+c＞0.其中正确的有（）A. 4个B. 3个C. 2个D. 1个2.（2020·杭州模拟）在平面直角坐标系中，已知m≠n，函数y=x²+（m+n）x+mn的图象与x轴有a个交点，函数y=mnx²+（m+n）x+1的图象与x轴有b个交点，则a与b的数量关系是（）A. a=bB. a=b-1C. a=b或a=b+1D. a=b或a=b-13.（2020·广西模拟）如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(−1,0)，其部分图象如图所示，下列结论：①2a+b=0；②b2−4ac<0；③当y>0时，x的取值范围是−1<x<3；④当x>0时，y随x增大而增大；⑤若t为任意实数，则有a+b≥at2+ bt，其中结论正确的个数是( )A. 4个B. 3个C. 2个D. 1个4.（2020·铁岭模拟）二次函数y=ax2+bx+c的图象如图所示，在下列说法中：①abc＞0；②a+b+c>0；③4a−2b+c>0；④当x>1时，y随着y的增大而增大.正确的说法个数是（）A. 1B. 2C. 3D. 45.（2020·东城模拟）若点A(1,y1),B(2,y2)在抛物线y=a(x+1)2+2(a<0)上，则下列结论正确的是（）A. 2>y1>y2B. 2>y2>y1C. y1>y2>2D. y2>y1>26.（2020·长丰模拟）若(−2,0)是二次函数y=ax2+bx(a>0)图象上一点，则抛物线y=a(x−2)2+ bx−2b的图象可能是（）A. B.C. D.7.（2020·南山模拟）已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1，其部分图象如图所示，下列说法中：①abc<0；②4a−2b+c<0；③若A（−12，y1）、B（32，y2）、C（−2，y3）是抛物线上的三点，则有y3<y1<y2；④若m，n（m<n）为方程a(x−3)(x+1)−2=0的两个根，则m>−1且n<3，以上说法正确的有（）A. ①②③④B. ②③④C. ①②④D. ①②③8.（2020·萧山模拟）已知二次函数y=a（x-2）2+c，当x=x1时，函数值为y1；当x=x2时，函数值为y2，若|x1-2|>|x2-2|，则下列表达式正确的是（）A. y1+y2>0B. y1-y2>0C. a（y1-y2）>0D. a（y1+y2）>09.（2020·西安模拟）二次函数y＝x2+bx+c的图象经过坐标原点O和点A(7，0)，直线AB交y轴于点B(0，﹣7)，动点C(x，y)在直线AB上，且1＜x＜7，过点C作x轴的垂线交抛物线于点D，则CD的最值情况是( )A. 有最小值9B. 有最大值9C. 有最小值8D. 有最大值810.（2020·广水模拟）二次函数y＝ax2+bx+c（a≠0）图象如图所示，下列结论：①abc＞0；②2a+b＝0；③当m≠1时，a+b＞am2+bm；④a−b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠ x2，则x1+x2＝2.其中正确的有（）A. ①②③B. ②④C. ②⑤D. ②③⑤11.（2020·铜川模拟）若一个二次函数y=ax2−4ax+3(x≠0)的图像经过两点A(m+2,y1)、B(2−m,y2)，则下列关系正确的是（）A. y1=y2B. y1<y2C. y1>y2D. y1≥y212.（2020·连云模拟）竖直向上的小球离地面的高度h（米）与时间t（秒）的关系函数关系式为h=-2t2+mt+25 8，若小球经过74秒落地，则小球在上抛过程中，第（）秒离地面最高.A. 37B. 47C. 34D. 4313.（2020·红花岗模拟）如图，抛物线y＝﹣x2+2x+c+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：①抛物线的对称轴是直线x＝1；②若OC＝OB，则c＝2；③若M（x0，y0）是x轴上方抛物线上一点，则（x0﹣a）（x0﹣b）＜0；④抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2.其中真命题个数是（）A. 1B. 2C. 3D. 414.（2020·柯桥模拟）在同一平面直角坐标系中，先将抛物线A：y＝x2﹣2通过左右平移得到抛物线B，再将抛物线B通过上下平移得到抛物线C：y＝x2﹣2x+2，则抛物线B的顶点坐标为（）A. （﹣1，2）B. （1，2）C. （1，﹣2）D. （﹣1，﹣2）15.（2020·台州模拟）抛物线y＝ax2+bx+c的顶点D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②a+b+c＞0；③c﹣a＝2；④方程ax2+bx+c ﹣2＝0有两个相等的实数根.其中正确的结论是（）A. ③④B. ②④C. ②③D. ①④16.（2020·绍兴模拟）抛物线y＝﹣x2+bx+c与x轴的两个交点坐标如图所示，下列说法中错误的是（）A. 一元二次方程﹣x2+bx+c＝0的解是x1＝﹣2，x2＝1B. 抛物线的对称轴是x=−12C. 当x＞1时，y随x的增大而增大D. 抛物线的顶点坐标是(−12,9 4 )17.（2020·湖州模拟）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac ＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（）A. 1B. 2C. 3D. 418.（2020·南充模拟）将抛物线y=x(x+2)向左平移1个单位后的解析式为（）A. y=x(x+1)B. y=x(x+3)C. y=(x−1)(x+1)D. y=(x+1)(x+3)19.（2020·沙湾模拟）二次函数y=−x2−1的图象是一条抛物线，下列关于该抛物线的说法正确的是（）A. 开口向上B. 对称轴是x=1C. 当x=0时，函数的最大值是-1D. 抛物线与x轴有两个交点20.（2020·峨眉山模拟）在平面直角坐标系中，已知a≠b，设函数y=(x+a)(x+b)的图像与x轴有M个交点，函数y=(ax+1)(bx+1)的图像与x轴有N个交点，则（）A. M=N−1或M=N+1B. M=N−1或M=N+2C. M=N或M=N+1D. M=N或M=N−121.（2020·峨眉山模拟）如图，二次函数y=ax2+bx+c(a≠0)的图象过点(−2,0)，对称轴为直线x= 1．有以下结论：①abc>0；②8a+c>0；③若A（x1，m），B（x2，m）是抛物线上的两点，当x=x1+x2时，y=c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取值范围为a≥1；3⑤若方程a(x+2)(4−x)=−2的两根为x1，x2，且x1＜x2，则﹣2≤ x1＜x2＜4．其中正确结论的序号是（）A. ①②④B. ①③④C. ①③⑤D. ①②③⑤22.（2020·旌阳模拟）已知y关于x的函数表达式是y=ax2−4x−a，下列结论错误的是（）A. 若a=−1，函数的最大值是5B. 若a=1，当x≥2时，y随x的增大而增大C. 无论a为何值时，函数图象一定经过点(1,−4)D. 无论a为何值时，函数图象与x轴都有两个交点23.（2020·新都模拟）关于二次函数y=x2−kx+k−1，以下结论：①抛物线交x轴有两个不同的交点；②不论k取何值，抛物线总是经过一个定点；③设抛物线交x轴于A、B两点，若AB=1，则k=4；④抛物线的顶点在y=−(x−1)2图象上；⑤抛物线交y轴于C点，若△ABC是等腰三角形，则k=−√2，0，1．其中正确的序号是（）A. ①②⑤B. ②③④C. ①④⑤D. ②④24.（2020·武侯模拟）如图是二次函数y＝ax2+bx+c的图象，其对称轴为直线x＝1，且与x轴的一个交点为A(3，0)，下列说法错误的是（）A. b2＞4acB. abc＜0C. 4a﹣2b+c＞0D. 当x＜﹣1时，y随x的增大而增大25.（2020·青白江模拟）已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，给出以下结论：①a+ b+c<0；②b2－4ac<0；③b+2a<0；④c<0.其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②26.（2020·大邑模拟）已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=−2，与x轴的一个交点坐标为(−4,0)，其部分图象如图所示，下列结论：①当x<0时，y随x增大而增大；②抛物线一定过原点；③方程ax2+bx+c=0(a≠0)的解为x=0或x=−4；④当−4<x<0时，ax2+bx+ c>0；⑤a−b+c<0．其中结论错误的．．．个数有（）个A. 1B. 2C. 3D. 427.（2020·永州模拟）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①b2＞4ac；②2a+b＝0；③3a+c＞0；④4a﹣2b+c＜0：⑤9a+3b+c＜0．其中结论正确的个数有（）A. 1个B. 2个C. 3个D. 4个28.（2020·怀化模拟）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=−1，下列结论：①abc＜0；②2a+b=0；③a﹣b+c＞0；④4a﹣2b+c＜0其中正确的是（）A. ①②B. 只有①C. ③④D. ①④29.（2020·黄石模拟）二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（）A. a＞0B. 当﹣1＜x＜3时，y＞0C. c＜0D. 当x≥1时，y随x的增大而增大30.（2020·乾县模拟）已知二次函数y=ax²-8ax（a为常数）的图象不经过第二象限，在自变量x的值满足2≤x≤3时，其对应的函数值y的最大值为3，则a的值为（）A. −14B. 14C. −15D. 15二、填空题31.（2020·海淀模拟）如图，在平面直角坐标系xOy中，有五个点A(2,0),B(0,−2),C(−2,4),D(4,−2),E(7,0)，将二次函数y=a(x−2)2+m(m≠0)的图象记为W．下列的判断中①点A一定不在W上；②点B，C，D可以同时在W上；③点C，E不可能同时在W上．所有正确结论的序号是________．32.（2020·长丰模拟）若抛物线y=x2−2kx+k2+1在−1≤x≤1时，始终在直线y=2的上方，则k的取值范围是________．33.（2020·新疆模拟）如图，二次函数y=ax2+bx+c(a≠0)的图象经过点(−12,0)，对称轴为直线x=1,下列5个结论：①abc<0；②a−2b+4c=0；③2a+b>0；④2c−3b<0；⑤a+b≤m(am+b).其中正确的结论为________. (注：只填写正确结论的序号)34.（2020·昌吉模拟）如图，抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(12,0)，有下列结论：①abc<0；②a﹣2b+4c=0；③25a﹣10b+4c=0；④3b+2c<0；⑤a﹣b≥m（am﹣b）；其中所有正确的结论是________.（填写正确结论的序号）35.（2020·立山模拟）若二次函数y=mx2+(m−2)x+m的顶点在x轴上，则m=________.36.（2020·立山模拟）在同一平面直角坐标系中，若抛物线y=x2+(2m−1)x+2m−4与y=x2−(3m+n)x+n关于y轴对称，则符合条件的m=________；n=________.37.（2020·铁西模拟）二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①4a+b＝0；②9a+c＞3b；③,3a+c＞0；④当x＞﹣1时，y的值随x值的增大而增大.⑤4a+2b≥am2−bm（m为任意实数）其中正确的结论有________.（填序号）38.（2020·梧州模拟）已知二次函数y=ax2+bx+c（a≠0）经过点A（1，-1）、B（3，3），且当1≤x≤3时，-1≤y≤3，则a的取值范围是________39.（2020·南充模拟）如图，抛物线y=x2+ax+2经过点P(−2，2)，Q(m，n).若点Q到y轴的距离小于2，则n的取值范围是________.40.（2020·海曙模拟）如图，已知△ABC中，∠ACB＝90°，D是斜边AB上一点，BD＝2AD，CD＝4，则S△ACD 的最大值为________.三、综合题41.如图，已知二次函数y=-x2+bx+c的图像经过点A（4，-5），点B（0，3）。

2020年中考数学模拟压轴题：二次函数1． 如图1，抛物线c bx x 31y 2++=经过A （，0）、B （0，﹣2）两点，点C 在y 轴上，△ABC 为等边三角形，点D 从点A 出发，沿AB 方向以每秒2个单位长度的速度向终点B 运动，设运动时间为t 秒（t ＞0），过点D 作DE ⊥AC 于点E ，以DE 为边作矩形DEGF ，使点F 在x 轴上，点G 在AC 或AC 的延长线上．（1）求抛物线的解析式；（2）将矩形DEGF 沿GF 所在直线翻折，得矩形D 'E 'GF ，当点D 的对称点D '落在抛物线上时，求此时点D '的坐标；（3）如图2，在x 轴上有一点M （，0），连接BM 、CM ，在点D 的运动过程中，设矩形DEGF 与四边形ABMC 重叠部分的面积为S ，直接写出S 与t 之间的函数关系式，并写出自变量t 的取值范围．2． 已知，如图，抛物线2(0)y ax bx c a =++≠的顶点为(1,9)M ，经过抛物线上的两点(3,7)A --和(3,)B m 的直线交抛物线的对称轴于点C ．（1）求抛物线的解析式和直线AB 的解析式．（2）在抛物线上,A M 两点之间的部分（不包含,A M 两点），是否存在点D ，使得2DAC DCM S S ∆∆=？若存在，求出点D 的坐标；若不存在，请说明理由．（3）若点P 在抛物线上，点Q 在x 轴上，当以点,,,A M P Q 为顶点的四边形是平行四边形时，直接写出满足条件的点P 的坐标．3． 自主学习，请阅读下列解题过程．解一元二次不等式：x 2﹣5x ＞0．解：设x 2﹣5x=0，解得：x 1=0，x 2=5，则抛物线y=x 2﹣5x 与x 轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x 2﹣5x 的大致图象（如图所示），由图象可知：当x ＜0，或x ＞5时函数图象位于x 轴上方，此时y ＞0，即x 2﹣5x ＞0，所以，一元二次不等式x 2﹣5x ＞0的解集为：x ＜0，或x ＞5． 通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：（1）上述解题过程中，渗透了下列数学思想中的 和 ．（只填序号）①转化思想 ②分类讨论思想 ③数形结合思想（2）一元二次不等式x 2﹣5x ＜0的解集为 ．（3）用类似的方法解一元二次不等式：x2﹣2x﹣3＞0．4．如图，直线y=12x+2与x轴交于点A，与y轴交于点B，抛物线y=-12x2+bx+c经过A、B两点，与x轴的另一个交点为C．（1）求抛物线的解析式；（2）根据图象，直接写出满足12x+2≥-12x2+bx+c的x的取值范围；（3）设点D为该抛物线上的一点、连接AD，若∠DAC=∠CBO，求点D 的坐标．5．如图，在矩形OABC中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在边OA上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．（1）求OE的长及经过O，D，C三点抛物线的解析式；（2）一动点P从点C出发，沿CB以每秒2个单位长度的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长度的速度向点C运动，当点P到达点B时，两点同时停止运动，设运动时间为t秒，当t为何值时，DP=DQ；（3）若点N在（1）中抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点坐标；若不存在，请说明理由．6．如图1，在平面直角坐标系中，抛物线y2x x与x 轴交于点A、B（点A在点B右侧），点D为抛物线的顶点，点C在y 轴的正半轴上，CD交x轴于点F，△CAD绕点C顺时针旋转得到△CFE，点A恰好旋转到点F，连接BE．（1）求点A、B、D的坐标；（2）求证：四边形BFCE是平行四边形；（3）如图2，过顶点D作DD1⊥x轴于点D1，点P是抛物线上一动点，过点P作PM⊥x轴，点M为垂足，使得△PAM与△DD1A相似（不含全等）．①求出一个满足以上条件的点P的横坐标；②直接回答这样的点P共有几个？7．如图已知抛物线y=-x2+（1-m）x-m2+12交x轴于点A，交y轴于点B （0，3），顶点C位于第二象限，连接AB，AC，BC．（1）求抛物线的解析式；（2）在x轴上是否存在点P，使得△PAB的面积等于△ABC的面积？如果存在，求出点P的坐标．（3）将△ABC沿x轴向右移动t个单位长度（0<t<1）时，平移后△ABC 和△ABO重叠部分的面积为S，求S与t之间的函数关系．8．已知抛物线G：y=mx2-2mx-3有最低点．（1）求二次函数y=mx2-2mx-3的最小值（用含m的式子表示）；（2）将抛物线G向右平移m个单位得到抛物线G1．经过探究发现，随着m的变化，抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；（3）记（2）所求的函数为H，抛物线G与函数H的图象交于点P，结合图象，求点P的纵坐标的取值范围．9．已知抛物线234 2y ax x=++的对称轴是直线3x=，与x轴相交于A，B两点（点B在点A右侧），与y轴交于点C．（1）求抛物线的解析式和A，B两点的坐标；（2）如图1，若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），是否存在点P，使四边形PBDC的面积最大？若存在，求点P的坐标及四边形PBDC面积的最大值；若不存在，请说明理由；（3）如图2，若点M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当3MN=时，求点M的坐标．10．如图，在平面直角坐标系中，圆M经过原点O，且与x轴、y轴分别相交于A（﹣8，0），B（0，﹣6）两点．（1）求出直线AB的函数解析式；（2）若有一抛物线的对称轴平行于y轴且经过点M，顶点C在圆M上，开口向下，且经过点B，求此抛物线的函数解析式；（3）设（2）中的抛物线交x轴于D、E两点，在抛物线上是否存在点P，使得S△PDE=S△ABC？若存在，请求出点P的坐标；若不存在，请说明理由．参考答案1．（1）把A（，0）、B（0，﹣2）代入抛物线的解析式得：，解得：，∴抛物线的解析式为．（2）A（，0）、B（0，﹣2），∴OA=，OB=2．∵AD=2t，∠DEA=90°，∠BAC=60°，∴AE=t，DE=t．∵△ABC为等边三角形，∴∠BAC=60°．∵AO⊥BC，∴∠CAO=∠BAO=30°．∵四边形DEGF为矩形，∴DF∥AC，GF=DE=t，∴∠DFA=∠CAO=30°，∴AF=2GF=t，∴∠DFA=∠BAO=30°，∴DF=AD=2t．过点D′作D′H⊥x轴与点H．∵∠D′FH=∠AFD=30°，∴D′H=D′F=t，FH=D′H=t，∴AH=AF+FH=t，∴OH=AH﹣AO=，∴D′（，t）．把点D′（，t）代入得：．整理得：9t2﹣10t=0，解得t=或t=0（舍去），∴D′（，）．（3）由（2）可知：DE =t ，DF =2t ，AE =t ．如图2所示：当AE +EG ≤AC 时，即t +2t ≤4，解得：t ≤．∴当0＜t ≤时，S =ED •DF =．当＜t ≤2时，如图3所示：∵CG =AG ﹣AC ，∴CG =3t ﹣4，∴GN =，∴S =ED •DF ﹣CG •GN =﹣（3t ﹣4）×（3t ﹣4）=．综上所述，S 与t 的函数关系式为．2． （1）二次函数表达式为：()219y a x =-+，将点A 的坐标代入上式并解得：1a =-，故抛物线的表达式为：228y x x =-++…①，则点()3,5B ，将点,A B 的坐标代入一次函数表达式并解得： 直线AB 的表达式为：21y x =-；（2）存在，理由：二次函数对称轴为：1x =，则点()1,1C ， 过点D 作y 轴的平行线交AB 于点H ，设点()2,28D x x x -++，点(),21H x x -， ∵2DAC DCM S S ∆∆=， 则()()()()()21112821139112222DAC C A S DH x x x x x x =-=-++-++=--⨯V ， 解得：1x =-或5（舍去5），故点()1,5D -；（3）设点(),0Q m 、点(),P s t ，228t s s =-++， ①当AM 是平行四边形的一条边时，点M 向左平移4个单位向下平移16个单位得到A ，同理，点(),0Q m 向左平移4个单位向下平移16个单位为()4,16m --，即为点P ，即：4m s -=，6t -=，而228t s s =-++， 解得：6s =或﹣4，故点()6,16P -或()4,16--； ②当AM 是平行四边形的对角线时，由中点公式得：2m s +=-，2t =，而228t s s =-++，解得：1s =±，故点()12P +或()12；综上，点()6,16P -或()4,16--或()12+或()12． 3．【答案】（1）①，③（2）0＜x ＜5（3）x ＜﹣1，或x ＞3． 4． （1）由y =12x +2可得： 当x =0时，y =2；当y =0时，x =-4， ∴A （-4，0），B （0，2），把A 、B 的坐标代入y =-12x 2+bx +c 得：322b c ⎧=-⎪⎨⎪=⎩，∴抛物线的解析式为：213222y x x =--+． （2）当x ≥0或x ≤-4时，12x +2≥-12x 2+bx +c ， （3）如图，过D 点作x 轴的垂线，交x 轴于点E ，由213222y x x =-+，令y =0， 解得：x 1=1，x 2=-4， ∴CO =1，AO =4， 设点D 的坐标为（m ，213222m m --+）， ∵∠DAC =∠CBO ， ∴tan ∠DAC =tan ∠CBO ，∴在Rt △ADE 和Rt △BOC 中有DE COAE BO =， 当D 在x 轴上方时，213212242--+=+m m m ， 解得：m 1=0，m 2=-4（不合题意，舍去）， ∴点D 的坐标为（0，2）．当D 在x 轴下方时，213(2)12242---+=+m m m ， 解得：m 1=2，m 2=-4（不合题意，舍去）， ∴点D 的坐标为（2，-3），故满足条件的D 点坐标为（0，2）或（2，-3）． 5． （1）∵CE=CB=5，CO=AB=4， ∴在Rt △COE 中，OE===3，设AD=m，则DE=BD=4﹣m，∵OE=3，∴AE=5﹣3=2，在Rt△ADE中，由勾股定理可得AD2+AE2=DE2，即m2+22=（4﹣m）2，解得m=，∴D（﹣，﹣5），∵C（﹣4，0），O（0，0），∴设过O、D、C三点的抛物线为y=ax（x+4），∴﹣5=﹣a（﹣+4），解得a=，∴抛物线解析式为y=x（x+4）=x2+x；（2）∵CP=2t，∴BP=5﹣2t，∵BD=，DE==，∴BD=DE，在Rt△DBP和Rt△DEQ中，，∴Rt△DBP≌Rt△DEQ（HL），∴BP=EQ，∴5﹣2t=t，∴t=；①当EN为对角线，即四边形ECNM是平行四边形时，则线段EN的中点横坐标为=﹣1，线段CM中点横坐标为，∵EN，CM互相平分，∴=﹣1，解得m=2，又M点在抛物线上，∴y=×22+×2=16，∴M（2，16）；②当EM为对角线，即四边形ECMN是平行四边形时，则线段EM的中点横坐标为，线段CN中点横坐标为=﹣3，∵EM，CN互相平分，∴=﹣3，解得m=﹣6，又∵M点在抛物线上，∴y=×（﹣6）2+×（﹣6）=16，∴M（﹣6，16）；③当CE为对角线，即四边形EMCN是平行四边形时，则M为抛物线的顶点，即M（﹣2，﹣）．综上可知，存在满足条件的点M，其坐标为（2，16）或（﹣6，16）或（﹣2，﹣）．6．（12x x+=0，解得x1=1，x2=–7．∴A（1，0），B（–7，0）．由y2x x-23)x+-得，D（–3，–）；（2）∵DD1⊥x轴于点D1，∴∠COF=∠DD1F=90°，∵∠D1FD=∠CFO，∴△DD1F∽△COF，∴11D D COFD OF=，∵D（–3，–），∴D1D OD=3，∵AC=CF，CO⊥AF，∴OF=OA=1，∴D 1F =D 1O –OF =3–1=21OC=， ∴OCCA =CF =FA =2，∴△ACF 是等边三角形，∴∠AFC =∠ACF ， ∵△CAD 绕点C 顺时针旋转得到△CFE ， ∴∠ECF =∠AFC =60°，∴EC ∥BF ， ∵EC =DC=6， ∵BF =6，∴EC =BF ，∴四边形BFCE 是平行四边形； （3）∵点P 是抛物线上一动点， ∴设P 点（x2x x +-）， ①当点P 在B 点的左侧时， ∵△PAM 与△DD 1A 相似， ∴11DD D A PM MA =或11DD D AAM PM=，41x =-=，解得：x 1=1（不合题意舍去），x 2=–11或x 1=1（不合题意舍去）x 2=–373； 当点P 在A 点的右侧时，∵△PAM 与△DD 1A 相似，∴11DD PM AM D A =或11D APM MA DD =，==，解得：x1=1（不合题意舍去），x2=–3（不合题意舍去）或x1=1（不合题意舍去），x2=–53（不合题意舍去）；当点P在AB之间时，∵△PAM与△DD1A相似，∴PMAM=11DDD A或PMMA=11D ADD，==，解得：x1=1（不合题意舍去），x2=–3（不合题意舍去）或x1=1（不合题意舍去），x2=–53；综上所述，点P的横坐标为–11或–373或–53；②由①得，这样的点P共有3个．7．（1）∵抛物线y=-x2+（1-m）x-m2+12交y轴于点B（0，3），∴-m2+12=3，∴m=±3．又∵抛物线的顶点C位于第二象限，∴-11m-<-，∴m>1，∴m=3，∴抛物线的解析式为y=-x2-2x+3．（2）过点C作CD⊥x轴，垂足为点D，如图1所示．当y=0时，-x2-2x+3=0，解得：x1=-3，x2=1，∴点A的坐标为（-3，0）．∵y=-x2-2x+3=-（x+1）2+4，∴点C的坐标为（-1，4），点D的坐标为（-1，0），∴S△ABC=S△ACD+S梯形CDOB-S△AOB=12AD·CD+12（OB+CD）·OD-12OA·OB=1 2×2×4+12×（3+4）×1-12×3×3=3．∵S△PAB=S△ABC，∴12AP·OB=3，∴AP=2，∴点P的坐标为（-1，0）或（-5，0）．（3）设△ABC平移后得到△A′B′C′，A′B′与y轴交于点M，A′C′交AB于点N，如图2所示．设线段AB 所在直线的解析式为y =kx +b （k ≠0）， 将A （-3，0），B （0，3）代入y =kx +b ，得：303k b b -+=⎧⎨=⎩，解得13k b =⎧⎨=⎩， ∴线段AB 所在直线的解析式为y =x +3．同理，可得出线段AC 所在直线的解析式为y =2x +6．∵将△ABC 沿x 轴向右移动t 个单位长度（0<t <1）得到△A ′B ′C ′， ∴点A ′的坐标为（t -3，0），线段A ′B ′所在直线的解析式为y =x +3-t （0<t <1），线段A ′C ′所在直线的解析式为y =2x +6-2t （0<t <1）． 当x =0时，y =x +3-t =3-t ，∴点M 的坐标为（0，3-t ）． 将y =x +3代入y =2x +6-2t ，整理，得：x +3-2t =0， 解得：x =2t -3，∴点N 的坐标为（2t -3，2t ）， ∴S =S △AOB -S △AA ′N -S △AA ′M =12OA ·OB -12AA ′·y A ′-12OA ′·OM =12×3×3-12t ·2t -12（3-t ）·（3-t ）= -32t 2+3t ． ∴S 与t 之间的函数关系式为S =-32t 2+3t （0<t <1）． 8． （1）∵y =mx 2-2mx -3=m （x -1）2-m -3，抛物线有最低点，∴二次函数y=mx2-2mx-3的最小值为-m-3．（2）∵抛物线G：y=m（x-1）2-m-3，∴平移后的抛物线G1：y=m（x-1-m）2-m-3，∴抛物线G1顶点坐标为（m+1，-m-3），∴x=m+1，y=-m-3，∴x+y=m+1-m-3=-2，即x+y=-2，变形得y=-x-2，∵m>0，m=x-1，∴x-1>0，∴x>1，∴y与x的函数关系式为y=-x-2（x>1）．（3）法一：如图，函数H：y=-x-2（x>1）图象为射线，x=1时，y=-1-2=-3；x=2时，y=-2-2=-4，∴函数H的图象恒过点B（2，-4），∵抛物线G：y=m（x-1）2-m-3，x=1时，y=-m-3；x=2时，y=m-m-3=-3，∴抛物线G恒过点A（2，-3），由图象可知，若抛物线与函数H的图象有交点P，则y B<y P<y A，∴点P纵坐标的取值范围为-4<y P<-3．法二：2223y x y mx mx =--⎧⎨=--⎩， 整理的：m （x 2-2x ）=1-x ，∵x >1，且x =2时，方程为0=-1不成立， ∴x ≠2，即x 2-2x =x （x -2）≠0， ∴m 1(2)xx x -=>-0，∵x >1， ∴1-x <0， ∴x （x -2）<0， ∴x -2<0， ∴x <2，即1<x <2， ∵y P =-x -2， ∴-4<y P <-3，9.（1）Q 抛物线的对称轴是直线3x =，3232a∴-=，解得14a =-， ∴∴抛物线的解析式为：213442y x x =-++．当0y =时，2134042x x -++=，解得12x =-，28x =，∴点A 的坐标为()2,0-，点B 的坐标为()8,0．答：抛物线的解析式为：213442y x x =-++；点A 的坐标为()2,0-，点B 的坐标为()8,0． （2）当0x =时，2134442y x x =-++=，∴点C 的坐标为()0,4． 设直线BC 的解析式为(0)y kx b k =+≠，将()8,0B ，()0,4C 代入y kx b =+得804k b b +==⎧⎨⎩，解得124k b =-=⎧⎪⎨⎪⎩， ∴直线BC 的解析式为142y x =-+．假设存在点P ，使四边形PBOC 的面积最大， 设点P 的坐标为213,442x x x ⎛⎫-++ ⎪⎝⎭，如图所示，过点P 作PD y ∥轴，交直线BC 于点D ，则点D 的坐标为1,42x x ⎛⎫-+ ⎪⎝⎭， 则2213114424224PD x x x x x ⎛⎫=-++--+=-+ ⎪⎝⎭， BOC PBC PBOC S S S ∆∆∴=+四边形1184?22PD OB =⨯⨯+ 211168224x x ⎛⎫=+⨯-+ ⎪⎝⎭2816x x =-++2(4)32x =--+∴当4x =时，四边形PBOC 的面积最大，最大值是3208x <<Q ，∴存在点()4,6P ，使得四边形PBOC 的面积最大．答：存在点P ，使四边形PBOC 的面积最大；点P 的坐标为()4,6，四边形PBOC 面积的最大值为32．（3）设点M 的坐标为213,442m m m ⎛⎫-++ ⎪⎝⎭，则点N 的坐标为1,42m m ⎛⎫-+⎪⎝⎭， 2213114424224MN m m m m m ⎛⎫∴=-++--+=-+ ⎪⎝⎭，又3MN =Q ，21234m m ∴-+=，当08m <<时，212304m m -+-=，解得12m =，26m =， ∴点M 的坐标为()2,6或()6,4；当0m <或8m >时，212304m m -++=，解得34m =-44m =+∴点M 的坐标为()41--或()41+-．答：点M 的坐标为()2,6、()6,4、()41--或()41+-．10.（1）设直线AB 的函数解析式为y=kx+b ，把A （﹣8，0），B （0，﹣6）代入得，解得，所以直线AB 的解析式为y=﹣x ﹣6；（2）在Rt △AOB 中，AB==10，∵∠AOB=90°，∴AB 为⊙M 的直径，∴点M 为AB 的中点，M （﹣4，﹣3），∵MC ∥y 轴，MC=5，∴C （﹣4，2）， 设抛物线的解析式为y=a （x+4）2+2， 把B （0，﹣6）代入得16a+2=﹣6，解得a=﹣，∴抛物线的解析式为y=﹣（x+4）2+2，即y=﹣x 2﹣4x ﹣6；（3）存在． 当y=0时，﹣（x+4）2+2=0，解得x 1=﹣2，x 2=﹣4，∴D （﹣6，0），E （﹣2，0）， S △ABC =S △ACM +S △BCM =8CM=20，设P（t，﹣t2﹣4t﹣6），∵S△PDE=S△ABC，∴（﹣2+6）|﹣t2﹣4t﹣6|=20，综上所述，P点坐标为（﹣4+，1）或（﹣4﹣，0）或（﹣4+，﹣1）或（﹣4﹣，0）时，使得S△PDE=S△ABC．。

2020年中考数学模拟试题分类汇编——二次函数一、选择题1．(2018年山东宁阳一模)在平面直角坐标系中，先将抛物线22-+=x x y 关于x 轴作轴对称变换，再将所得抛物线关于y 轴作轴对称变换，通过两次变换后所得的新抛物线解析式为〔 〕A ．22+--=x x yB ．22-+-=x x yC ．22++-=x x yD ．22++=x x y 答案：C2．(2018年江西省统一考试样卷)假设抛物线y =2x 2向左平移1个单位，那么所得抛物线是〔 〕A ．y =2x 2＋1B ．y =2x 2－1C ．y =2〔x ＋1〕2D ．y =2〔x －1〕2答案：C3. 〔2018年河南中考模拟题1〕某校运动会上，某运动员掷铅球时，他所掷的铅球的高 与水平的距离，那么该运动员的成绩是( )A. 6mB. 10mC. 8mD. 12m答案：D 4．〔2018年河南中考模拟题4〕二次函数2y ax bx c =++〔0a ≠〕的图象如下图，那么正确的选项是( )A ．a ＜0B ．b ＜0C ．c ＞0D ．以答案上都不正确 答案：A5.〔2018年河南中考模拟题3〕二次函数y=ax 2+bx+c 的图像如下图，那么以下条件正确的选项是〔 〕 A ．ac ＜0 B.b 2－4ac ＜0 C. b ＞0 D. a ＞0、b ＜0、c ＞0 答案：D6．(2018年江苏省泰州市济川实验初中中考模拟题)抛物线y ＝ax 2＋bx ＋c 上部分点的横坐标x ，纵坐标y 的对应值如表所示．yxOx= 1y– 1 33O x第9题P1 第11题xyO1给出以下讲法：①抛物线与y 轴的交点为(0，6)； ②抛物线的对称轴是在y 轴的右侧； ③抛物线一定通过点(3，0)； ④在对称轴左侧，y 随x 增大而减小． 从表中可知，以下讲法正确的个数有( ) A ．1个B ．2个C ．3个D ．4个7.〔2018天水模拟〕二次函数y=ax2+bx+c 的图像如下图，那么关于此二次函数的以下四个结论①a<0②a>0③b 2-4ac>0④0<ab中，正确的结论有〔 〕 A.1个 B.2个 C.3个 D.4个 答案：C8.(2018年厦门湖里模拟)抛物线y =322+-x x 与坐标轴交点为 〔 〕 A ．二个交点 B ．一个交点 C ．无交点 D ．三个交点 答案：B9．(2018年厦门湖里模拟)如图，抛物线)0(2>++=a c bx ax y 的P 〔3，0〕，那么 对称轴是直线1=x ，且通过点的值为A. 0B. －1C. 1D. 2 答案：A10．〔2018年杭州月考〕二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如下图，给出以下结论：①0<abc ②当1x =时，函数有最大值。

2018-2020年广东中考数学各地区模拟试题分类（深圳专版）（一）——二次函数一．选择题1．（2020•深圳模拟）二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x＝1，下列结论：①abc＜0；②b＜c；③3a+c＝0；④对于任意实数m，a+b≥am2+bm．其中正确的结论有（）A．1个B．2个C．3个D．4个2．（2020•深圳模拟）如图，抛物线y＝ax2+bx+c经过点（﹣1，0），与y轴交于（0，2），抛物线的对称轴为直线x＝1，则下列结论中：①a+c＝b；②方程ax2+bx+c＝0的解为﹣1和3；③2a+b＝0；④c﹣a＞2，其中正确的结论有（）A．1个B．2个C．3个D．4个3．（2020•盐田区二模）二次函数y＝ax2+bx+c的图象如图所示，则下列结论正确的是（）A．abc＞0 B．a+b+c＝0 C．4a﹣2b+c＜0 D．b2﹣4ac＜0 4．（2020•罗湖区一模）如图是二次函数y＝ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x＝1，下列结论正确的是（）A．b2＜4ac B．ac＞0 C．a﹣b+c＝0 D．2a﹣b＝0 5．（2020•福田区模拟）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x1，0）、（x2，0），其中0＜x2＜1，有下列结论：①b2﹣4ac＞0；②4a﹣2b+c＞﹣1；③﹣3＜x1＜﹣2；④当m为任意实数时，a﹣b≤am2+bm；⑤3a+c ＝0．其中，正确的结论有（）A．②③④B．①③⑤C．②④⑤D．①③④6．（2020•龙华区二模）定义：在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成的周长值与面积值相等，则这个点叫做和谐点，这个矩形叫做和谐矩形．已知点P（m，n）是抛物线y＝x2+k上的和谐点，对应的和谐矩形的面积为16，则k的值为（）A．﹣12 B．0 C．4 D．16 7．（2020•宝安区二模）如图，抛物线y＝ax2+bx+c（a≠0）的顶点为P（﹣1，0），则下列结论错误的是（）A．b＞0B．a＝cC．当x＞0时，y随x的增大而增大D．若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝28．（2020•福田区一模）阅读材料：坐标平面内，对于抛物线y＝ax2+bx（a≠0），我们把点（﹣）称为该抛物线的焦点，把y＝﹣称为该抛物线的准线方程．例如，抛物线y＝x2+2x的焦点为（﹣1，﹣），准线方程是y＝﹣．根据材料，现已知抛物线y＝ax2+bx（a≠0）焦点的纵坐标为3，准线方程为y＝5，则关于二次函数y＝ax2+bx 的最值情况，下列说法中正确的是（）A．最大值为4 B．最小值为4C．最大值为3.5 D．最小值为3.59．（2020•光明区一模）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①bc＞0；②3a+c＞0；③a+b+c≤ax2+bx+c；④a（k12+1）2+b（k12+1）＞a（k12+2）2+b（k12+2）．其中正确结论的个数是（）A ．1B ．2C ．3D ．410．（2020•福田区校级模拟）二次函数y ＝ax 2+bx +c （a ，b ，c 为常数，且a ≠0）中的x 与y 的部分对应值如表：x … ﹣1 0 1 3 … y…﹣1353…下列结论错误的是（ ） A ．ac ＜0B ．3是关于x 的方程ax 2+（b ﹣1）x +c ＝0的一个根C ．当x ＞1时，y 的值随x 值的增大而减小D ．当﹣1＜x ＜3时，ax 2+（b ﹣1）x +c ＞0 二．填空题11．（2020•龙岗区校级模拟）如图，已知抛物线y 1＝﹣2x 2+2，直线y 2＝2x +2，当x 任取一值时，x 对应的函数值分别为y 1、y 2．若y 1≠y 2，取y 1、y 2中的较小值记为M ；若y 1＝y 2，记M ＝y 1＝y 2．例如：当x ＝1时，y 1＝0，y 2＝4，y 1＜y 2，此时M ＝0．下列判断： ①当x ＞0时，y 1＞y 2； ②当x ＜0时，x 值越大，M 值越小；③使得M 大于2的x 值不存在； ④使得M ＝1的x 值是﹣或．其中正确的是 ．12．（2019•福田区校级模拟）将抛物线y ＝x 2先向左平移2个单位，再向下平移3个单位，所得抛物线的解析式为 ．13．（2019•深圳模拟）如图，四边形OABC 是边长为1的正方形，OC 与x 轴正半轴的夹角为15°，点B 在抛物线y ＝ax 2（a ＜0）的图象上，则a 的值为 ．14．（2018•深圳模拟）抛物线y＝x2+2x+3的对称轴是直线x＝．15．（2018秋•福田区校级月考）二次函数y＝x2+bx+c的图象如图所示，则函数值y＜0时，对应x的取值范围是．三．解答题16．（2020•深圳模拟）如图，已知二次函数y＝ax2+c的图象与x轴分别相交于点A（﹣5，0），点B，与y轴相交于C（0，﹣5），点Q是抛物线在x轴下方的一动点（不与C点重合）．（1）求该二次函数的表达式；（2）如图1，AQ交线段BC于D，令t＝，当t值最大时，求Q点的坐标．（3）如图2，直线AQ，BQ分别与y轴相交于M，N两点，设Q点横坐标为m，S1＝S△QMN，S2＝πm2，试问是否为定值？若是，求出该定值；若不是，请说明理由．17．（2020•深圳模拟）如图，抛物线y＝x2+bx+c与直线y＝﹣x+3分别交于x轴，y轴上的B、C两点，设该抛物线与x轴的另一个交点为A，顶点为D，连接CD交x轴于点E．（1）求该抛物线的解析式；（2）点F，G是对称轴上两个动点，且FG＝2，点F在点G的上方，请求出四边形ACFG 的周长的最小值；（3）连接BD，若P在y轴上，且∠PBC＝∠DBA+∠DCB，请直接写出点P的坐标．18．（2020•大鹏新区一模）如图1，经过点B（1，0）的抛物线y＝a（x+1）2﹣与y轴交于点C，其顶点为点G，过点C作y轴的垂线交抛物线对称轴于点D，线段CO上有一动点M，连接DM、DG．（1）求抛物线的表达式；（2）求GD+DM+MO的最小值以及相应的点M的坐标；（3）如图2，在（2）的条件下，以点A（﹣2，0）为圆心，以AM长为半径作圆交x轴正半轴于点E．在y轴正半轴上有一动点P，直线PF与⊙A相切于点F，连接EF交y轴于点N，当PF∥BM时，求PN的长．19．（2020•盐田区二模）如图，抛物线y＝ax2+bx﹣3经过点A（3，0），B（﹣1，0），与y轴交于点C，点P是抛物线在第四象限内的一点．（1）求抛物线解析式；（2）点D是线段OC的中点，OP⊥AD，点E是射线OP上一点，OE＝AD，求DE的长；（3）连接CP，AP，是否存在点P，使得OP平分四边形ABCP的面积？若存在，求点P的坐标；若不存在，说明理由．20．（2020•罗湖区一模）如图，已知抛物线y ＝a （x +2）（x ﹣4）（a 为常数，且a ＞0）与x 轴从左至右依次交于A ，B 两点，与y 轴交于点C ，经过点B 的直线y ＝﹣x +与抛物线的另一交点为D ，且点D 的横坐标为﹣5． （1）求抛物线的函数表达式；（2）该二次函数图象上有一点P （x ，y ）使得S △BCD ＝S △ABP ，求点P 的坐标； （3）设F 为线段BD 上一点（不含端点），连接AF ，求2AF +DF 的最小值．参考答案一．选择题1．解：①对称轴位于x轴的右侧，则a，b异号，即ab＜0．抛物线与y轴交于正半轴，则c＞0．∴abc＜0．故①正确；②∵抛物线开口向下，∴a＜0．∵抛物线的对称轴为直线x＝﹣＝1，∴b＝﹣2a．∵x＝﹣1时，y＝0，∴a﹣b+c＝0，而b＝﹣2a，∴c＝﹣3a，∴b﹣c＝﹣2a+3a＝a＜0，即b＜c，故②正确；③∵x＝﹣1时，y＝0，∴a﹣b+c＝0，而b＝﹣2a，∴c＝﹣3a，∴3a+c＝0．故③正确；＝a+b+c，当x＝m时，y＝am2+bm+c，因此有a+b≥am2+bm，④当x＝1时，y最大故④正确；综上所述，正确的结论有：4个，故选：D．2．解：①∵抛物线y＝ax2+bx+c经过点（﹣1，0），∴a﹣b+c＝0，∴a+c＝b，故本选项正确；②由对称轴为x＝1，一个交点为（﹣1，0），∴另一个交点为（3，0），∴方程ax2+bx+c＝0的解为﹣1和3，故本选项正确；③由对称轴为x＝1，∴﹣＝1，∴b＝﹣2a，则2a+b＝0，故本选项正确；④∵抛物线y＝ax2+bx+c与y轴交于（0，2），∴c＝2，∵a＜0，∴c﹣a＞2，故本选项正确；故选：D．3．解：由图象可得，a＞0，b＜0，c＜0，∴abc＞0，故选项A正确；当x＝1时，y＝a+b+c＜0，故选项B错误；当x＝﹣2时，y＝4a﹣2b+c＞0，故选项C错误；该函数图象与x轴两个交点，则b2﹣4ac＞0，故选项D错误；故选：A．4．解：A．∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，所以A选项错误；B．∵抛物线开口向上，∴a＞0，∵抛物线与y轴的交点在x轴下方，∴c＜0，∴ac＜0，所以B选项错误；C．∵抛物线过点A（3，0），二次函数图象的对称轴是x＝1，∴抛物线与x轴的另一个交点为（﹣1，0），∴a﹣b+c＝0，所以C选项正确；D．∵二次函数图象的对称轴是直线x＝1，∴﹣＝1，∴2a+b＝0，所以D选项错误；故选：C．5．解：∵二次函数y＝ax2+bx+c（a≠0）的图象与x轴有两个交点，∴b2﹣4ac＞0，故①正确；∵该函数图象的对称轴是x＝﹣1，当x＝0时的函数值小于﹣1，∴x＝﹣2时的函数值和x＝0时的函数值相等，都小于﹣1，∴4a﹣2b+c＜﹣1，故②错误；∵该函数图象的对称轴是x＝﹣1，与x轴的交点为（x1，0）、（x2，0），其中0＜x2＜1，∴﹣3＜x，1＜﹣2，故③正确；∵当x＝﹣1时，该函数取得最小值，∴当m为任意实数时，则a﹣b+c≤am2+bm+c，即a﹣b≤am2+bm，故④正确；∵＝﹣1，∴b＝2a，∵x＝1时，y＝a+b+c＞0，∴3a+c＞0，故⑤错误；故选：D．6．解：∵点P（m，n）是抛物线y＝x2+k上的点，∴n＝m2+k，∴k＝n﹣m2，∴点P（m，n）是和谐点，对应的和谐矩形的面积为16，∴2|m|+2|n|＝|mn|＝16，∴|m|＝4，|n|＝4，当n≥0时，k＝n﹣m2＝4﹣16＝﹣12；当n＜0时，k＝n﹣m2＝﹣4﹣16＝﹣20．故选：A．7．解：A．由开口方向知a＞0，结合对称轴在y轴左侧知b＞0，此选项正确；B．将（﹣1，0）代入解析式得a﹣b+c＝0，由x＝﹣＝﹣1知b＝2a，则a﹣2a+c＝0，整理得a＝c，此选项正确；C．当x＞0时，函数图象自左向右逐渐上升，所以此时y随x的增大而增大，此选项正确；D．若ax12+bx1＝ax22+bx2，且x1≠x2，则＝﹣1，即x1+x2＝﹣2，此选项错误；故选：D．8．解：根据题意得＝3，﹣＝5，解得a＝﹣，b＝2或b＝﹣2，∴抛物线y＝ax2+bx（a≠0）的解析式为y＝﹣x2+2x或y＝﹣x2﹣2x，∵y＝﹣x2+2x＝﹣（x﹣4）2+4，y＝﹣x2﹣2x＝﹣（x+4）2+4，∴二次函数y＝ax2+bx有最大值4．故选：A．9．解：①由图象可以看出，a＜0，b＞0，c＞0，故bc＞0，正确，符合题意；②函数的对称轴为x＝1＝﹣，即b＝﹣2a，根据函数的对称性可知x＝﹣1时，y＜0，即a﹣b+c＜0，故3a+c＜0，故②错误，不符合题意；③抛物线在x＝1时，取得最大值，即a+b+c≥ax2+bx+c，故③错误，不符合题意；④x＝k2+1≥1，而在对称轴右侧，y随x增大而减小，∵+1＜+2，∴a（k12+1）2+b（k12+1）+c＞a（k12+2）2+b（k12+2）+c，故a（k12+1）2+b（k12+1）＞a（k12+2）2+b（k12+2）正确，符合题意；故选：B．10．解：根据x与y的部分对应值可知：当x＝﹣1时，y＝﹣1，即a﹣b+c＝﹣1；当x＝0时，y＝3，即c＝3；当x＝1时，y＝5，即a+b+c＝5；∴，解得：，∴y＝﹣x2+3x+3．A、ac＝﹣1×3＝﹣3＜0，故本选项正确；B、方程ax2+（b﹣1）x+c＝0可化为方程ax2+bx+c＝x，由表格数据可知，x＝3时，y＝3，则3是方程ax2+bx+c＝x的一个根，从而也是方程ax2+（b﹣1）x+c＝0的一个根，故本选项正确；C、∵当x＝0时，y＝3；x＝3时，y＝3，∴二次函数y＝ax2+bx+c的对称轴为x＝＝，又∵二次项系数a＝﹣1，抛物线开口向下，∴当1＜x＜时，y的值随x值的增大而增大，故C错误；D、不等式ax2+（b﹣1）x+c＞0可化为：ax2+bx+c＞x，即y＞x，∵由表格可知，（﹣1，﹣1），（3，3）均在直线y＝x上，又抛物线y＝ax2+bx+c开口向下，∴当﹣1＜x＜3时，y＞x，故D正确．综上，只有选项C错误．故选：C．二．填空题（共5小题）11．解：当x ＞0时，一次函数图象位于二次函数上方，∴y 2＞y 1故①错误；∵当x ＜0，两个函数的函数随着x 的增大而增大，∴当x 越大时，M 越大，故②错误；函数y 1＝﹣2x 2+2有最大值，最大值为y 1＝2，∴不存在使得M 大于2的x 的值，故③正确；令y 1＝1，即：﹣2x 2+2＝1．解得：x 1＝，x 2＝﹣不题意舍去）令y 2＝1，得：2x +2＝1，解得：x ＝﹣．故④正确． 故答案为：③④．12．解：抛物线y ＝x 2的顶点坐标为（0，0），把点（0，0）先向左平移2个单位，再向下平移3个单位得到对应点的坐标为（﹣2，﹣3），所以平移后的抛物线解析式为y ＝（x +2）2﹣3．故答案为y ＝（x +2）2﹣3．13．解：如图，连接OB ，∵四边形OABC 是边长为1的正方形，∴∠BOC ＝45°，OB ＝1×＝， 过点B 作BD ⊥x 轴于D ，∵OC 与x 轴正半轴的夹角为15°，∴∠BOD ＝45°﹣15°＝30°，∴BD ＝OB ＝，OD ＝＝， ∴点B 的坐标为（，﹣）， ∵点B 在抛物线y ＝ax 2（a ＜0）的图象上，∴a （）2＝﹣， 解得a ＝﹣．故答案为：﹣．14．解：∵y＝x2+2x+3＝（x+1）2+2，∴对称轴是直线x＝﹣1，故答案为：﹣1．15．解：∵抛物线顶点坐标为（﹣1，﹣4），二次项系数为1，∴抛物线的解析式为：y＝（x+1）2﹣4即y＝x2+2x﹣3＝（x+3）（x﹣1）∴抛物线与x轴两交点坐标为（﹣3，0），（1，0）故当函数值y＜0时，对应x的取值范围上是﹣3＜x＜1．本题答案为﹣3＜x＜1．三．解答题（共5小题）16．解：（1）把A（﹣5，0），C（0，﹣5）两点坐标代入y＝ax2+c，得到，解得，∴二次函数的解析式为y＝x2﹣5．（2）如图1中，过点Q作QE⊥AB交BC于E．设Q（m，m2﹣5），由（1）可知，A（﹣5，0），B（5，0），C（0，﹣5），∴直线BC的解析式为y＝x﹣5，直线AQ的解析式为y＝x+m﹣5，由，解得，∴D（，），∴E（m2，m2﹣5），∵QE∥AB，∴△QED∽△ABD，∴t＝＝＝＝﹣m2+m，∵﹣＜0，∴当m＝﹣＝时，t的值最大，此时Q（，﹣）．（3）是定值．理由：如图2中，设Q（m，m2﹣5），由（2）可知，直线AQ的解析式为y＝x+m﹣5，当x＝0时，y＝m﹣5，∴M（0，m﹣5），∵直线BQ的解析式为y＝x﹣m﹣5，当x＝0时，y＝﹣m﹣5，∴N（0，﹣m﹣5），∴S1＝S△MNQ＝×m×（2m）＝m2，∴＝＝，为定值．17．解：（1）∵直线y＝﹣x+3分别交x轴，y轴于B，C两点，∴B（6，0），C（0，3），把B（6，0），C（0，3）代入y＝x2+bx+c，得，解得：，∴抛物线的解析式为：y＝x2﹣2x+3；（2）∵抛物线的解析式为y＝x2﹣2x+3∴y＝（x2﹣8x）+3＝（x﹣4）2﹣1，∴抛物线的对称轴为x＝4，D（4，﹣1）；∵A（2，0），C（0，3），∴AC＝＝，∵FG＝2，∴AC+FG的值为+2，若四边形ACFG的周长最小，则CF+AG最小即可，将点C向下平移2个单位得到N（0，1），连结BN，与对称轴的交点即为所求点G'．在对称轴上将点G'向上平移2个单位得到点F'．此时四边形ACF'G'的周长最小，∴CF'+AG'＝NG'+BG'＝BN＝＝＝，∴四边形ACFG的周长的最小值为+2+；（3）∵C（0，3），D（4，﹣1），∴直线CD的解析式为y＝﹣x+3，∴E（3，0），∴OE＝OC＝3，∴∠AEC＝45°，∵tan∠DBE＝＝，tan∠OBC＝＝，∴tan∠DBE＝tan∠OBC，∴∠DBE＝∠OBC，则∠PBC＝∠DBA+∠DCB＝∠AEC＝45°，①当点P在y轴负半轴上时，如图2，过点P作PG⊥BC交BC于点G，则∠GPC＝∠OBC，∴tan∠GPC＝，设CG＝a，则GP＝2a，∵∠CBP＝45°，∴BG＝GP，∵C（0，3），B（6，0），∴OC＝3，OB＝6，∴BC＝3，即：2a+a＝3，解得：a＝，∴CG＝a＝，PG＝2，∴PC＝＝5，∴OP＝2，故点P（0，﹣2）；②当点P在y轴正半轴时，同理可得：点P（0，18）；故点P的坐标为（0，﹣2）或（0，18）．18．解：（1）∵抛物线y＝a（x+1）2﹣，经过点B（1，0），∴0＝4a﹣，∴a＝∴．（2）过点O作直线l与x轴夹角为α，且，α＝45°，过点M作MH⊥直线l于H，则有，∴，∴，∴，∴当D，M，H共线时，的值最小，∵D（﹣1，﹣），直线l的解析式为y＝﹣x，∴直线DH的解析式为y＝x﹣，由，解得，∴H（，﹣），M（0，﹣），∴DH＝＝，∵DG＝﹣+＝，∴的最小值＝+＝．（3）如图2中，连接BM，延长FA交y轴于J．∵A（﹣2，0），M（0，﹣），∴AM＝AF＝＝，∵B（1，0），∴直线BM的解析式为y＝x﹣，∵PF是⊙A的切线，∴PF⊥AF，∵PF∥BM，∴AF⊥BM，∴直线AF的解析式为y＝﹣x﹣，∴J（0，﹣），∴AJ＝＝，∴FJ＝AF+AJ＝+，∵PF∥BM，∴∠FPJ＝∠OMB，∴tan∠FPJ＝tan∠OMB，∴＝，∴＝，∴PF＝+，∵AF＝AE，∴∠AFE＝∠AEF，∵∠AFE+∠PFN＝90°，∠AEN+∠ONE＝90°，∠PNF＝∠ENO，∴∠PFN＝∠PNF，∴PN＝PF＝+．19．解：（1）∵抛物线y＝ax2+bx﹣3经过点A（3，0），B（﹣1，0），∴，解得：，∴抛物线解析式为：y＝x2﹣2x﹣3；（2）如图，连接CE，∵∠AOD＝90°，∴∠AOE+∠COE＝90°，∵AD⊥OE，∴∠AOE+∠OAD＝90°，∴∠OAD＝∠COE，∵抛物线y＝x2﹣2x﹣3与y轴交于点C，∴点C（0，﹣3），∴OC＝OA＝3，又∵AD＝OE，∴△OAD≌△COE（SAS），∴∠AOD＝∠OCE＝90°，OD＝CE，∵点D是线段OC的中点，∴OD＝DC＝，∴CE＝＝DC，又∵∠DCE＝90°，∴DE＝DC＝；（3）过P作PN⊥x轴于N，交AC于M，∵点C（0，﹣3），A（3，0），∴直线AC解析式为：y＝x﹣3，设点P（m，m2﹣2m﹣3）（m＞0），则点M（m，m﹣3），∴MP＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，∴四边形ABCP的面积＝×4×3+×3×（﹣m2+3m）＝﹣m2+m+6，∵OP平分四边形ABCP的面积，∴×3×（﹣m2+2m+3）＝×（﹣m2+m+6），∴m1＝2，m2＝﹣1（舍去），∴P点坐标为（2，﹣3）．20．解：（1）抛物线y＝a（x+2）（x﹣4），令y＝0，解得x＝﹣2或x＝4，∴A（﹣2，0），B（4，0）．∵直线y＝﹣x+，当x＝﹣5时，y＝3，∴D（﹣5，3），∵点D（﹣5，3）在抛物线y＝a（x+2）（x﹣4）上，∴a（﹣5+2）（﹣5﹣4）＝3，∴a＝．∴抛物线的函数表达式为：y＝x2﹣x﹣．（2）如图1中，设直线BD交y轴于J，则J（0，）．连接CD，BC．＝××9＝10，∵S△BDC＝10，∴S△PAB∴×6×|y P|＝10y＝±，P当y＝时，＝x2﹣x﹣，解得x＝1±，∴P（，）或（，），当﹣＝x2﹣x﹣，方程无解，∴满足条件的点P的坐标为（，）或（，）．（3）如图2中，过点D作DM平行于x轴，∵D（﹣5，3），B（4，0），∴tan∠DBA＝＝，∴∠DBA＝30°∴∠BDM＝∠DBA＝30°，过F作FJ⊥DM于J，则有sin30°＝，∴JF＝，∴2AF+DF＝2（AF+）＝2（AF+JF），当A、F、J三点共线时，即AJ⊥DM时，2AF+DF＝2（AF+JF）取最小值为＝．。

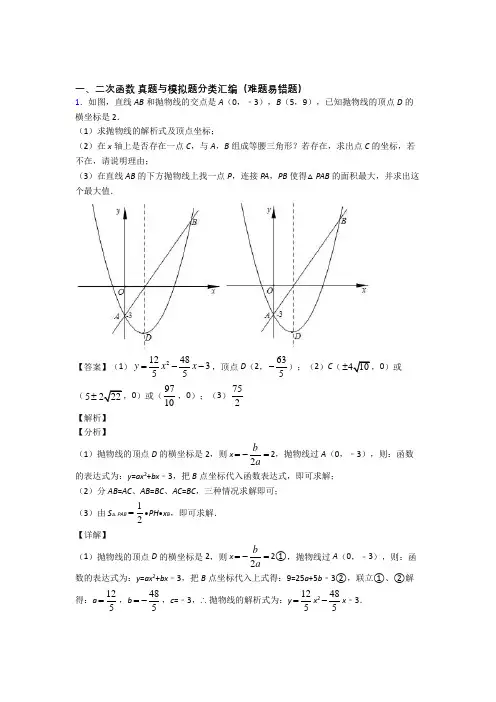
一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，直线AB 和抛物线的交点是A （0，﹣3），B （5，9），已知抛物线的顶点D 的横坐标是2．（1）求抛物线的解析式及顶点坐标；（2）在x 轴上是否存在一点C ，与A ，B 组成等腰三角形？若存在，求出点C 的坐标，若不在，请说明理由；（3）在直线AB 的下方抛物线上找一点P ，连接PA ，PB 使得△PAB 的面积最大，并求出这个最大值．【答案】（1）21248355y x x =--，顶点D （2，635-）；（2）C （10±0）或（5222±0）或（9710，0）；（3）752【解析】 【分析】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入函数表达式，即可求解； （2）分AB =AC 、AB =BC 、AC =BC ，三种情况求解即可；（3）由S △PAB 12=•PH •x B ，即可求解． 【详解】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2①，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入上式得：9=25a +5b ﹣3②，联立①、②解得：a 125=，b 485=-，c =﹣3，∴抛物线的解析式为：y 125=x 2485-x ﹣3．当x=2时，y635=-，即顶点D的坐标为（2，635-）；（2）A（0，﹣3），B（5，9），则AB=13，设点C坐标（m，0），分三种情况讨论：①当AB=AC时，则：（m）2+（﹣3）2=132，解得：m=±410，即点C坐标为：（410，0）或（﹣410，0）；②当AB=BC时，则：（5﹣m）2+92=132，解得：m=5222±，即：点C坐标为（5222+，0）或（5﹣222，0）；③当AC=BC时，则：5﹣m）2+92=（m）2+（﹣3）2，解得：m=9710，则点C坐标为（9710，0）．综上所述：存在，点C的坐标为：（±410，0）或（5222±，0）或（9710，0）；（3）过点P作y轴的平行线交AB于点H．设直线AB的表达式为y=kx﹣3，把点B坐标代入上式，9=5k﹣3，则k125=，故函数的表达式为：y125=x﹣3，设点P坐标为（m，12 5m2485-m﹣3），则点H坐标为（m，125m﹣3），S△PAB12=•PH•x B52=（125-m2+12m）=－6m2+30m=25756()22m--+，当m=52时，S△PAB取得最大值为：752．答：△PAB的面积最大值为752．【点睛】本题是二次函数综合题．主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．2．如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1, 0）、C（3, 0）、D（3,4）．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，以每秒12个单位的速度沿线段AD向点D运动，运动时间为t秒．过点P作PE⊥x轴交抛物线于点M，交AC 于点N．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）当t为何值时，△ACM的面积最大？最大值为多少？（3）点Q从点C出发，以每秒1个单位的速度沿线段CD向点D运动，当t为何值时，在线段PE上存在点H，使以C、Q、N、H为顶点的四边形为菱形？【答案】（1）A（1，4）；y＝－x2＋2x＋3；（2）当t＝２时，△AＭC面积的最大值为1；（3）2085或20 13．【解析】（1）由矩形的性质得到点A的坐标，由抛物线的顶点为A，设抛物线的解析式为y＝a（x －1）2＋4，把点C的坐标代入即可求得a的值；（2）由点P的坐标以及抛物线解析式得到点M的坐标，由A、C的坐标得到直线AC的解析式，进而得到点N的坐标，即可用关于t的式子表示MN，然后根据△ACM的面积是△AMN和△CMN的面积和列出用t表示的△ACM的面积，利用二次函数的性质即可得到当t＝２时，△AＭC面积的最大值为1；（3）①当点Ｈ在Ｎ点上方时，由PＮ＝CQ，PN∥CQ，得到四边形PNCQ为平行四边形，所以当PQ＝CQ时，四边形FECQ为菱形，据此得到，解得t值；②当点Ｈ在Ｎ点下方时，NH=CQ=，NQ＝CQ时，四边形NHCQ为菱形，NQ2＝CQ2，得：，解得t值．解：（1）由矩形的性质可得点A（1，4），∵抛物线的顶点为A，设抛物线的解析式为y＝a（x－1）2＋4，代入点C （3, 0），可得a ＝－1． ∴y ＝－（x －1）2＋4＝－x 2＋2x ＋3． （2）∵P （112t +，４）， 将112x t =+代入抛物线的解析式，y ＝－（x －1）2＋4＝2144t -， ∴M （112t +，2144t -）， 设直线AC 的解析式为，将A （１,４），C （３,０）代入，得：，将112x t =+代入得，∴N （112t +，），∴MN ，∴，∴当t ＝２时，△A ＭC 面积的最大值为1． （3）①如图１，当点Ｈ在Ｎ点上方时， ∵Ｎ（112t +，），P （112t +，４）， ∴P Ｎ＝４—（）＝＝CQ ，又∵PN ∥CQ ，∴四边形PNCQ 为平行四边形， ∴当PQ ＝CQ 时，四边形FECQ 为菱形， PQ 2＝PD 2+DQ 2 ＝，∴，整理，得240800t t -+=．解得12085t =-，22085t =+（舍去）；②如图２当点Ｈ在Ｎ点下方时，NH=CQ=，NQ ＝CQ 时，四边形NHCQ 为菱形， NQ 2＝CQ 2，得：．整理，得213728000t t -+=．()()1320400t t --=．所以12013t =，（舍去）．“点睛”此题主要考查二次函数的综合问题，会用顶点式求抛物线，会用两点法求直线解析式，会设点并表示三角形的面积，熟悉矩形和菱形的性质是解题的关键.3．抛物线2y x bx c =-++（b ，c 为常数）与x 轴交于点()1,0x 和()2,0x ，与y 轴交于点A ，点E 为抛物线顶点。

2020年中考数学二次函数真题汇编(名师精选全国真题，值得下载练习)一、单选题1.如图，一段抛物线y=﹣x 2+4（﹣2≤x≤2）为C 1 ， 与x 轴交于A 0 ， A 1两点，顶点为D 1；将C 1绕点A 1旋转180°得到C 2 ， 顶点为D 2；C 1与C 2组成一个新的图象，垂直于y 轴的直线l 与新图象交于点P 1（x 1 ， y 1），P 2（x 2 ， y 2），与线段D 1D 2交于点P 3（x 3 ， y 3），设x 1 ， x 2 ， x 3均为正数，t=x 1+x 2+x 3 ， 则t 的取值范围是（ ）A. 6＜t≤8 B. 6≤t≤8 C. 10＜t≤12 D. 10≤t≤12 【答案】D【解析】【解答】解：翻折后的抛物线的解析式为y=（x ﹣4）2﹣4=x 2﹣8x+12， ∵设x 1 ， x 2 ， x 3均为正数，∴点P 1（x 1 ， y 1），P 2（x 2 ， y 2）在第四象限， 根据对称性可知：x 1+x 2=8， ∵2≤x 3≤4，∴10≤x 1+x 2+x 3≤12即10≤t≤12， 故答案为：D ．【分析】根据题意可求出翻折后的抛物线的解析式，设x 1 ， x 2 ， x 3均为正数，可得出点P 1（x 1 ， y 1），P 2（x 2 ， y 2）在第四象限，根据对称性可求出x 1+x 2=8，由2≤x 3≤4，可得出x 1+x 2+x 3的取值范围，从而得出t 的取值范围。

2.已知，平面直角坐标系中，直线y 1=x+3与抛物线y=-x x 的图象如图，点P 是y 2上的一个动点，则点P 到直线y 1的最短距离为（ ）A.B.C. D.【答案】D【解析】【解答】解、∵点P 到直线y 1的距离最短， ∴点P 是直线与抛物线相切时的交点。

设直线y 1平移k 个单位长度，则此时的解析式为 =x+3+k ， 把 =x+3+k 代入y=-x 2+2x 整理得，-x 2+x-3-k=0，△=b 2-4ac=1-4 (-) (-3-k)=0，解得k=-，即直线y 1向下平移个单位长度与抛物线相切， 把k=-代入解析式解方程组可求得点P 的坐标为（1，）；过点P 作PD ⊥直线y 1于点D ，则直线PD 的解析式可设为y 3=-x+b ，把点P （1，）代入可求得b=,即直线PD 的解析式为y 3=-x+，将y 1和y 3的解析式联立解方程组可求得点D 的坐标为（-，）；若直线PD与x轴相较于点C，直线y1=x+3与x、y轴分别相较于点A、B，易得点A （-3,0）、B（0,3），∴∠BAC==∠DCA，由勾股定理可得：CD=，CP=，∴PD=CD-CP=。

2020年上海市16区中考数学二模汇编专题13 二次函数（解答题24题压轴题）1. （2020闵行二模）2.（2020松江二模）3.（2020宝山二模）4.（2020奉贤二模）5.（2020金山二模）6.（2020静安二模）7.（2020嘉定二模）8.（2020长宁二模）9.（2020崇明二模） 10.（2020浦东二模） 11.（2020徐汇二模） 12.（2020青浦二模） 13.（2020虹口二模） 14（2020杨浦二模） 15（2020黄浦二模） 16.（2020普陀二模）1.（2020闵行二模）在平面直角坐标系xOy 中，我们把以抛物线2y x 上的动点A 为顶点的抛物线叫做这条抛物线的“子抛物线”．如图，已知某条“子抛物线”的二次项系数为32，且与y 轴交于点C ．设点A 的横坐标为m （m ＞0），过点A 作y 轴的垂线交y 轴于点B ．（1）当m=1时，求这条“子抛物线”的解析式； （2）用含m 的代数式表示∠ACB 的余切值； （3）如果∠OAC=135°，求m 的值．2.（2020松江二模） 如图，在平面直角坐标系xOy 中，抛物线与x 轴和y 轴的正半轴分别交于A 、B 两点，且OA=OB ，又抛物线的顶点为M ，联结AB 、AM . （1）求这条抛物线的表达式和点M 的坐标； （2）求的值；（3）如果Q 是线段OB 上一点，满足∠MAQ=45°，求点Q 的坐标.23y x bx =-++sin BAM ∠3.（2020宝山二模）如图6，在平面直角坐标系xOy 中，抛物线()2230y ax ax a a =--<与x 轴交于A B 、两点（点A 在点B 的左侧），经过点A 的直线:l y kx b =+与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且4CD AC =.（1）直接写出点A 的坐标，并求直线l 的函数表达式（其中k b 、用含a 的式子表示） （2）点E 是直线l 上方的抛物线上的动点，若ACE ∆的面积的最大值为54，求a 的值； （3）设P 是抛物线的对称轴上的一点，点Q 在抛物线上，当以点A D P Q 、、、为顶点的四边形为矩形时，请直接写出点P 的坐标.4.（2020奉贤二模） 如图7，在平面直角坐标系中，抛物线2yx bx 经过点A (2，0)．直线xOy122y x =-与x 轴交于点B ，与y 轴交于点C ． （1）求这条抛物线的表达式和顶点的坐标； （2）将抛物线2y x bx 向右平移，使平移后的抛物线经过点B ，求平移后抛物线的表达式；（3）将抛物线2yx bx 向下平移，使平移后的抛物线交y 轴于点D ，交线段BC 于点P 、Q ，（点P 在点Q 右侧），平移后抛物线的顶点为M ，如果DP ∥x 轴，求∠MCP 的正弦值．5.（2020金山二模）在平面直角坐标系xOy 中（如图），已知抛物线2y x bx c =-++经过点A （3，0）和点B （0，3），其顶点为C ．（1）求抛物线的解析式和顶点C 的坐标；（2）我们把坐标为（n ，m ）的点叫做坐标为（m ，n ）的点的反射点，已知点M 在这条抛物线上，它的反射点在抛物线的对称轴上，求点M 的坐标；（3）点P 是抛物线在第一象限部分上的一点，如果∠POA =∠ACB ，求点P 的坐标．6.（2020静安二模）在平面直角坐标系xOy 中（如图9），已知抛物线c bx x y ++-=221（其中b 、c 是常数）经过点A （-2，-2）与点B （0，4），顶点为M ． （1）求该抛物线的表达式与点M 的坐标；（2）平移这条抛物线，得到的新抛物线与y 轴交于点C （点C 在点B 的下方），且△BCM 的面积为3．新抛物线的对称轴l 经过点A ，直线l 与x 轴交于点D ．①求点A 随抛物线平移后的对应点坐标；②点E 、G 在新抛物线上，且关于直线l 对称，如果正方形DEFG 的顶点F 在第二象限内，求点F 的坐标．7.（2020嘉定二模）在平面直角坐标系xOy 中（如图7），已知经过点)0,3(-A 的抛物线322-+=ax ax y与y 轴交于点C ，点B 与点A 关于该抛物线的对称轴对称，D 为该抛物线的顶点. （1）直接写出该抛物线的对称轴以及点B 的坐标、点C 的坐标、点D 的坐标； （2）联结AD 、DC 、CB ，求四边形ABCD 的面积；（3）联结AC .如果点E 在该抛物线上，过点E 作x 轴的垂线， 垂足为H ，线段EH 交线段AC 于点F.当FH EF 2=时，求点E 的坐标.8（2020长宁二模）如图7，在平面直角坐标系xOy 中，已知抛物线n mx x y ++=2经过点)2-2(，A ，对称轴是直线1=x ，顶点为点B ，抛物线与y 轴交于点C .（1）求抛物线的表达式和点B 的坐标；（2）将上述抛物线向下平移1个单位， 平移后的抛物线与x 轴正半轴交于点D ，求BCD ∆的面积； （3）如果点P 在原抛物线上，且在对称轴的右侧，联结BP 交线段OA 于点Q ，51=PQ BQ ，求点P 的坐标.y x-3-3-2-2-1-11AO19.（2020崇明二模）已知抛物线24y ax bx =+-经过点(1,0),(4,0)A B -，与y 轴交于点C ，点D 是该抛物线上一点，且在第四象限内，连接AC BC CD BD 、、、．（1）求抛物线的函数解析式，并写出对称轴； （2）当4BCD AOC S S ∆∆=时，求点D 的坐标；（3）在（2）的条件下，如果点E 是x 轴上一点，点F 是抛物线上一点，当以点A D E F 、、、为顶点的四边形是平行四边形时，请直接写出点E 的坐标．10.（2020浦东二模）在平面直角坐标系xOy 中，已知抛物线2y x bx c =-++与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点(0,3)C ，对称轴是直线1x =．（1）求抛物线的表达式；（2）直线MN 平行于x 轴，与抛物线交于M 、N 两点（点M 在点N 的左侧），且34MN AB =，点C 关于直线MN 的对称点为E ，求线段OE 的长；（3）点P 是该抛物线上一点，且在第一象限内，联结CP 、EP ，EP 交线段BC 于点F ，当:1:2CPF CEF S S =△△时，求点P 的坐标．11.（2020徐汇二模） .如图，已知直线22y x =+与x 轴交于点A ，与y 轴交于点C ，矩形ACBE 的顶点B 在第一象限的反比例函数my x=图像上，过点B 作BF ⊥OC ，垂足为F ，设OF=t ．（1）求∠ACO 的正切值；（2）求点B 的坐标（用含t 的式子表示）； （3）已知直线22y x =+与反比例函数my x=图像都经过第一象限的点D ，联结DE ，如果DE x ⊥轴，求m 的值．12.（2020青浦二模）如图7，在平面直角坐标系xOy 中，二次函数243y a x a x =-+ 的图像与x 轴正半轴交于点A 、B ，与y 轴相交于点C ，顶点为D ，且tan 3∠=CAO ．（1）求这个二次函数的解析式；（2）点P 是对称轴右侧抛物线上的点，联结CP ，交对称轴于点F ，当:2:3CDFFDPS S=时，求点P 的坐标；（3）在（2）的条件下，将△PCD 沿直线MN 翻折，当点P 恰好与点O 重合时，折痕MN 交轴于点M ，交轴于点N ，求OM ON的值．x y13. （2020•虹口区二模）如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx +3经过点A （﹣1，0）和点B （3，0），该抛物线对称轴上的点P 在x 轴上方，线段PB 绕着点P 逆时针旋转90°至PC （点B 对应点C ），点C 恰好落在抛物线上．（1）求抛物线的表达式并写出抛物线的对称轴； （2）求点P 的坐标；（3）点Q 在抛物线上，联结AC ，如果∠QAC ＝∠ABC ，求点Q 的坐标．14（2020杨浦二模）如图，已知在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx +4经过点A （-3，0）和点B （3，2），与y 轴相交于点C .（1）求这条抛物线的表达式；（2）点P 是抛物线在第一象限内一点，联结AP ，如果点C 关于直线AP 的对称点D 恰好落在x 轴上，求直线AP 的截距；（3）在第（2）小题的条件下，如果点E 是y 轴正半轴上一点，点F 是直线AP 上一点．当△EAO 与△EAFyx DO CBAyxDO CBA全等时，求点E 的纵坐标．15（2020黄浦二模）在平面直角坐标系xOy 中，已知抛物线y＝21x 2+bx+c 经过点A （﹣4，0）和B （2，6），其顶点为D ．（1）求此抛物线的表达式； （2）求△ABD 的面积；（3）设C 为该抛物线上一点，且位于第二象限，过点C 作CH ⊥x 轴，垂足为点H ，如果△OCH 与△ABD 相似，求点C 的坐标．16.（2020普陀二模）2020年上海市16区中考数学二模汇编专题13 二次函数（解答题24题压轴题）2.（2020闵行二模） 2.（2020松江二模）3.（2020宝山二模）4.（2020奉贤二模）5.（2020金山二模）6.（2020静安二模）7.（2020嘉定二模）8.（2020长宁二模）9.（2020崇明二模） 10.（2020浦东二模） 11.（2020徐汇二模） 12.（2020青浦二模）13.（2020虹口二模） 14（2020杨浦二模） 15（2020黄浦二模） 16.（2020普陀二模）1.（2020闵行二模）在平面直角坐标系xOy中，我们把以抛物线2y x上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”．如图，已知某条“子抛物线”的二次项系数为32，且与y轴交于点C．设点A的横坐标为m（m＞0），过点A作y轴的垂线交y轴于点B．（1）当m=1时，求这条“子抛物线”的解析式；（2）用含m的代数式表示∠ACB的余切值；（3）如果∠OAC=135°，求m的值．【分析】（1）先求出m=1时点A的坐标，进而可得到这条“子抛物线”的解析式；（2）先根据A点坐标求出“子抛物线”的解析式和AB,OB的长度，然后令x = 0求出y值即可得到C点坐标，进而可求出BC的长度，最后利用cotBCACBAB∠=即可求解；（3）过O点作OD⊥CA的延长线于点D，过点D作y轴的平行线分别交BA的延长线于点E，交x轴于点F, 首先证明△AED≌△DFO，则有AE=DF，DE=OF，设AE=n，那么DF=n，BE= m + n=OF=ED，通过OB=EF得到22m m n=+，然后再通过cotDEADEAE∠=得到32m nmn+=，将两个关于m,n的方程联立即可求出m 的值．【详解】解：（1）∵点A 在2y x 上，点A 的横坐标为m ，∴A （m ，m 2），当m =1时，21m = ，∴A （1，1），∴这条“子抛物线”的解析式为23(1)12y x =-+． （2）由A （m ，m 2），且AB ⊥y 轴，可得AB =m ，OB = m 2．∴“子抛物线”的解析式为223()2y x m m =-+． 令x = 0，252y m =， ∴点C 的坐标（0，252m ），252OC m =， ∴232BC OC OB m =-=． 在Rt △ABC 中，2332cot 2m BC ACB m AB m ∠===．（3）如图，过O 点作OD ⊥CA 的延长线于点D ，过点D 作y 轴的平行线分别交BA 的延长线于点E ，交x 轴于点F ．∵∠OAC=135°，∴∠OAD=45°．又∵OD ⊥CA ，90ADO ∴=︒∴∠AOD=∠OAD=45°，∴AD=OD ，90,90EAD ADE ODF ADE ∠+∠=︒∠+∠=︒ ，EAD ODF ∴∠=∠．90DEA DFO ∠=∠=︒，∴△AED ≌△DFO ，∴AE=DF ，DE=OF ．设AE=n ，那么DF=n ，BE= m + n=OF=ED ．又∵OB=EF ，∴22m m n =+．又//EF OC ∴，∴∠BCA=∠ADE ， ∴3cot 2DE m n ADE m AE n +∠===． 解方程组2232m m n m n m n⎧=+⎪⎨+=⎪⎩，得12m =，213m =-（舍去） ， m 的值为2．【点睛】本题主要考查全等三角形的判定及性质，锐角三角函数的应用，子抛物线的定义，掌握全等三角形的判定及性质，锐角三角函数的定义是解题的关键．2.（2020松江二模） 如图，在平面直角坐标系xOy 中，抛物线与x 轴和y 轴的正半轴分别交于A 、B 两点，且OA=OB ，又抛物线的顶点为M ，联结AB 、AM .（1）求这条抛物线的表达式和点M 的坐标；（2）求的值；（3）如果Q 是线段OB 上一点，满足∠MAQ=45°，求点Q 的坐标.23y x bx =-++sin BAM ∠解：（1）∵抛物线23y x bx =-++与y 轴交于B 点令x=0得y=3,∴B (0,3) ………………………………………………………………1分∵AO=BO,∴A (3,0) …………………………………………………………………1分把A (3,0)代入23y x bx =-++,得9330b -++=解得b=2,∴这条抛物线的表达式y =-x 2+2x +3 ………………………………………1分顶点M (1,4) ……………………………………………………………………………1分（2）∵ A (3,0)，B (0,3) M (1,4)，∴22BM =,218AB =,220AM =∴∠MBC =90°………………………………………………………………………2分 ∴210sin =1025BM BAM AM ∠==………………………………………………………2分 （3）∵OA=OB,∴∠OAB =45°∵∠MAQ=45°,∴∠BAM=∠OAQ ………………………………………………1分由(2)得10sin 10BAM ∠=,∴10sin 10OAQ ∠= ∴1tan 3OAQ ∠= ……………………………………………………………………1分 ∴133OQ OQ OA ==,∴1OQ = …………………………………………………………1分 ∴Q (0,1) ………………………………………………………………………………1分(3)另解∵OA=OB,∴∠OAB =45°∵∠MAQ=45°,∴∠BAM=∠OAQ ………………… ………………………………1分由（2）可知1tan 3BAM ∠=,∴1tan 3OAQ ∠= ……………………………………1分∴133OQ OQ OA ==,∴1OQ = ……………………………………………………………1分 ∴Q (0,1) ………………………………………………………………………………1分3.（2020宝山二模）如图6，在平面直角坐标系xOy 中，抛物线()2230y ax ax a a =--<与x 轴交于A B 、两点（点A 在点B 的左侧），经过点A 的直线:l y kx b =+与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且4CD AC =.（1）直接写出点A 的坐标，并求直线l 的函数表达式（其中k b 、用含a 的式子表示）（2）点E 是直线l 上方的抛物线上的动点，若ACE ∆的面积的最大值为54，求a 的值； （3）设P 是抛物线的对称轴上的一点，点Q 在抛物线上，当以点A D P Q 、、、为顶点的四边形为矩形时，请直接写出点P 的坐标.【解答】解：（1）当y ＝ax 2﹣2ax ﹣3a ＝a （x +1）（x ﹣3），得A （﹣1，0），B （3，0），∵直线l ：y ＝kx +b 过A （﹣1，0），∴0＝﹣k +b ，即k ＝b ，∴直线l ：y ＝kx +k ，∵抛物线与直线l 交于点A ，D ，∴ax 2﹣2ax ﹣3a ＝kx +k ，即ax 2﹣（2a +k ）x ﹣3a ﹣k ＝0，∵CD ＝4AC ，∴点D的横坐标为4，∴﹣3−ka=−1×4，∴k＝a，∴直线l的函数表达式为y＝ax+a；（2）如图1，过E作EF∥y轴交直线l于F，设E（x，ax2﹣2ax﹣3a），则F（x，ax+a），EF＝ax2﹣2ax﹣3a﹣ax﹣a＝ax2﹣3ax﹣4a，∴S△ACE＝S△AFE﹣S△CEF=12（ax2﹣3ax﹣4a）（x+1）−12（ax2﹣3ax﹣4a）x=12（ax2﹣3ax﹣4a）=12a（x−32）2−258a，∴△ACE的面积的最大值═258 a，∵△ACE的面积的最大值为5 4，∴−258a=54，解得a=−2 5；（3）以点A、D、P、Q为顶点的四边形能成为矩形，令ax2﹣2ax﹣3a＝ax+a，即ax2﹣3ax﹣4a＝0，解得：x1＝﹣1，x2＝4，∴D（4，5a），∵抛物线的对称轴为直线x＝1，设P（1，m），①如图2，若AD是矩形ADPQ的一条边，则易得Q（﹣4，21a），∴m＝21a+5a＝26a，则P（1，26a），∵四边形ADPQ是矩形，∴∠ADP＝90°，∴AD2+PD2＝AP2，∴52+（5a）2+32+（26a﹣5a）2＝22+（26a）2，即a2=1 7，∵a＜0，∴a=−√7 7∴P（1，−26√7 7）；②如图3，若AD是矩形APDQ的对角线，则易得Q （2，﹣3a ），∴m ＝5a ﹣（﹣3a ）＝8a ，则P （1，8a ），∵四边形APDQ 是矩形，∴∠APD ＝90°，∴AP 2+PD 2＝AD 2，∴（﹣1﹣1）2+（8a ）2+（1﹣4）2+（8a ﹣5a ）2＝52+（5a ）2，即a 2=14，∵a ＜0，∴a =−12，∴P （1，﹣4），综上所述，点A 、D 、P 、Q 为顶点的四边形能成为矩形，点P （1，−26√77）或（1，﹣4）．4.（2020奉贤二模）如图7，在平面直角坐标系中，抛物线2y x bx 经过点A (2，0)．直线122y x =-与x 轴交于点B ，与y 轴交于点C ． （1）求这条抛物线的表达式和顶点的坐标；（2）将抛物线2y x bx 向右平移，使平移后的抛物线经过点B ，求平移后抛物线的表达式；xOy（3）将抛物线2y x bx 向下平移，使平移后的抛物线交y 轴于点D ，交线段BC 于点P 、Q ，（点P 在点Q 右侧），平移后抛物线的顶点为M ，如果DP ∥x 轴，求∠MCP 的正弦值．解：（1）由题意，抛物线2yx bx 经过点A (2，0)， 得042b ， 解得 2b ···················································································· （2分） ∴抛物线的表达式是22y x x =-. ··················································································· （1分） 它的顶点C 的坐标是（1，-1）. ························································································· （1分）（2）∵直线122y x =-与x 轴交于点B ， ∴点B 的坐标是(4，0) . ···························· （1分） ①将抛物线22y x x =-向右平移2个单位，使得点A 与点B 重合，此时平移后的抛物线表达式是231（）y x =--. ································································ （2分） ②将抛物线22y x x =-向右平移4个单位，使得点O 与点B 重合，此时平移后的抛物线表达式是251（）y x =--. ································································ （1分） （3）设向下平移后的抛物线表达式是：22y x x n =-+，得点D （0，n ）.∵DP ∥x 轴，∴点D 、P 关于抛物线的对称轴直线1x对称，∴P （2，n ）.∵点P 在直线BC 上，∴12212n =⨯-=-. ∴平移后的抛物线表达式是：222y x x =--. ································································ （2分） ∴新抛物线的顶点M 的坐标是（1，-2）. ······································································· （1分）B CA xyo∴MC //OB ，∴∠MCP =∠OBC ．在Rt △OBC 中，sin OC OBC BC ， 由题意得：OC =2，25BC， ∴5sin sin 25MCP OBC . ·············································································· （1分） 即∠MCP 的正弦值是5. 5.（2020金山二模）在平面直角坐标系xOy 中（如图），已知抛物线2y x bx c =-++经过点A （3，0）和点B （0，3），其顶点为C ．（1）求抛物线的解析式和顶点C 的坐标；（2）我们把坐标为（n ，m ）的点叫做坐标为（m ，n ）的点的反射点，已知点M 在这条抛物线上，它的反射点在抛物线的对称轴上，求点M 的坐标；（3）点P 是抛物线在第一象限部分上的一点，如果∠POA =∠ACB ，求点P 的坐标．解：（1），抛物线2y x bx c =-++经过点A （3，0）和点B （0，3），，23303b c c ⎧-++=⎨=⎩,--------------------------------------------------------------------------------（1分） ，b =2，c =3，抛物线的解析式为223y x x =-++，--------------------------------------（2分） 顶点C 的坐标为（1，4）.---------------------------------------------------------------------------（1分）（2）设点M 的坐标为（t ，223t t -++），点M 的反射点为（223t t -++，t ），------------------------------------------------------------（1分） 由抛物线的对称轴为直线x =1，得223=1t t -++，----------------------------------------（1分）解得：1t 2=1t ，∴M 的坐标为（1）或（1-，1）.--------（2分） （3）过点P 作PH ，x 轴，垂足为点H ，由A （3，0）、点B （0，3）、点C （1，4），得AB=AC =BC ，，222AB BC AC +=，∴∠ABC =90°，tan 3AB ACB BC ∠===，----（1分） ∵∠POA =∠ACB ，∴tan 3POH ∠=，∵∠PHO =90°，∴tan 3PHPOH OH∠==， 设PH =3s ，OH =s ，由点P 在第一象限得点P 的坐标是（s ，3s ）,∴2233s s s -++=--------------------------------------------------------------------------（1分）解得11=2s -+，21=2s --（不合题意，舍去），∴1=2s -+，--（1分）点P ）.-----------------------------------------------（1分）6.（2020静安二模）在平面直角坐标系xOy 中（如图9），已知抛物线c bx x y ++-=221（其中b 、c 是常数）经过点A （-2，-2）与点B （0，4），顶点为M ． （1）求该抛物线的表达式与点M 的坐标；（2）平移这条抛物线，得到的新抛物线与y 轴交于点C （点C 在点B 的下方），且△BCM 的面积为3．新抛物线的对称轴l 经过点A ，直线l 与x 轴交于点D ．①求点A 随抛物线平移后的对应点坐标；②点E 、G 在新抛物线上，且关于直线l 对称，如果正方形DEFG 的顶点F 在第二象限内，求点F 的坐标．.解：（1）将A （-2，-2）、B （0，4）代入c bx x y ++-=221得，21(2)22200 4.b c c ⎧-⨯--+=-⎪⎨⎪++=⎩，·············································································· （2分） 解得⎩⎨⎧==.42c b ，∴该抛物线的表达式为：42212++-=x x y ； ···················································· （1分） 顶点M 的坐标是：（2，6）． ···················································································· （1分） （2）①∵平移后抛物线的对称轴经过点A （-2，-2），∴可设平移后的抛物线表达式为：k x y ++-=2)221（． ····································· （1分） ∴C （0，-2+ k ）．∴32)]2(4[21221=⋅+--=⋅=∆k BC S BCM ，························································· （1分） 解得k=3． ∴3)2212++-=x y （． ······································································· （1分）即原抛物线向左平移4个单位，向下平移3个单位可以得到新的抛物线．∴点A 对应点的坐标为（-6，-5）． ········································································· （1分） ②设EG 与DF 的交点为H ． 在正方形DEFG 中，EG ⊥DF ，EG =DF =2EH =2DH ．∵点E 、G 是这条抛物线上的一对对称点，∴EG //x 轴． ∴DF ⊥x 轴，由此可设F （-2，2a ）．∵点F 在第二象限内，∴a >0．∴EG =DF =2EH =2DH =2a ．不妨设点E 在点G 的右侧，那么E （-2 +a ，a ）． ··················································· （1分） 将点E 代入3)2212++-=x y （得：a a =+-3212． ············································· （1分） 解得171-=a ，172--=a （不合题意，舍去）．········································· （1分）∴F （-2，272-）． ································································································ （1分）7.（2020嘉定二模）在平面直角坐标系xOy 中（如图7），已知经过点)0,3(-A 的抛物线322-+=ax ax y 与y 轴交于点C ，点B 与点A 关于该抛物线的对称轴对称，D 为该抛物线的顶点. （1）直接写出该抛物线的对称轴以及点B 的坐标、点C 的坐标、点D 的坐标； （2）联结AD 、DC 、CB ，求四边形ABCD 的面积；（3）联结AC .如果点E 在该抛物线上，过点E 作x 轴的垂线， 垂足为H ，线段EH 交线段AC 于点F.当FH EF 2=时，求点E 的坐标.解：（1）该抛物线的对称轴为直线1-=x ······································································ 1分点B 的坐标为（1，0）. ················································································· 1分 点C 的坐标为（0，-3）. ················································································ 1分 点D 的坐标为（-1，-4）. ··············································································· 1分（2）过点D 作AB DM ⊥，垂足为M ，易得：1=OM ，4=DM ，2=AM ，1=OB .4422121=⨯⨯=⋅=DM AM S ADM △， ·································································· 1分 271432121=⨯+=⋅+=）（（梯形OM )DM OC S OCDM ， ············································ 1分 23312121=⨯⨯=⋅=OC OB S OBC △， ······································································ 1分 所以923274=++=++=OBC OCDM ADM ABCD S S S S △梯形△四边形 ································ 1分 y x-3-3-2-2-1-11AO1（3）设直线AC 的表达式为b kx y +=，∵)0,3(-A ，)3,0(-C 在直线b kx y +=上，∴⎩⎨⎧-=+-=330b b k .解得⎩⎨⎧-=-=31b k ，故直线AC 的表达式为3--=x y . ····························· 1分方法1.∵点F 在直线3--=x y 上，所以可设)3,(--x x F .∵AB EH ⊥，点F 在线段EH 上，且HF EF 2=，可得)93,(--x x E . ································ 1分 ∵)93,(--x x E 在抛物线322-+=x x y 上，∴32932-+=--x x x . ································· 1分 整理，得 0652=++x x .解得 21-=x ，32-=x (不符合题意，应舍去).8（2020长宁二模）如图7，在平面直角坐标系xOy 中，已知抛物线n mx x y ++=2经过点)2-2(，A ，对称轴是直线1=x ，顶点为点B ，抛物线与y 轴交于点C .（1）求抛物线的表达式和点B 的坐标；（2）将上述抛物线向下平移1个单位， 平移后的抛物线与x 轴正半轴交于点D ，求BCD ∆的面积； （3）如果点P 在原抛物线上，且在对称轴的右侧，联结BP 交线段OA 于点Q ，51=PQ BQ ，求点P 的坐标.x解：（1） 抛物线n mx x y ++=2经过点)2,2(-A ，对称轴是直线1=x∴42212m n m ++=-⎧⎪⎨-=⎪⎩，解得22m n =-⎧⎨=-⎩ （2分）∴抛物线的解析式为222y x x =--，顶点B 的坐标是(1,3)- （2分） （2）抛物线222y x x =--与y 轴交于点），（2-0C 平移后的抛物线表达式为： 223y x x =-- ，点D 的坐标是(3,0) （2分） 过点B 做y BH ⊥轴，垂足为点H ∴=S S S BCD BCH COD BHOD S ∆∆∆--梯形1111=(13)31123=22222⨯+⨯-⨯⨯-⨯⨯ （2分） （3）∵直线OA 经过点00O （，）、)2,2(-A ，∴直线OA 的表达式为：y x =- 设对称轴与直线OA 相交于点E ，则11E （，-） ∵ (1,3)B - ∴2BE = （1分） 过点P 作PF//BE ，交直线OA 于点F设点）（22,2--t t t P 1t >（），则）（t t F -, ∴22PF t t =-- （1分） ∵ PF//BE ∴15BE BQ PF PQ == ∴22125t t =-- ∴2120t t --= ∴3t =- （舍去）或4t = （1分） ∴)6,4(P （1分）9.（2020崇明二模）已知抛物线24y ax bx =+-经过点(1,0),(4,0)A B -，与y 轴交于点C ，点D 是该抛物线上一点，且在第四象限内，连接AC BC CD BD 、、、．（1）求抛物线的函数解析式，并写出对称轴； （2）当4BCD AOC S S ∆∆=时，求点D 的坐标；（3）在（2）的条件下，如果点E 是x 轴上一点，点F 是抛物线上一点，当以点A D E F 、、、为顶点的四边形是平行四边形时，请直接写出点E 的坐标．【整体分析】（1）根据点A ，B 的坐标，利用待定系数法可求出抛物线的解析式，即可写出对称轴；（2）连接OD ，求出C 点坐标，根据A 、B 、C 点坐标求出8BCD S ∆=，设2(,34)D x x x --，根据=16OCD OBD OBC BCD OCDB S S S S S ∆∆∆∆=++=四边形，列出关于x 的方程，解方程即可求出D 点坐标；（3）分两种情形：如图2中，当AE 为平行四边形的边时，根据DF=AE=1，求解即可．如图3中，当AE ，DF 是平行四边形的对角线时，根据点F 的纵坐标为6，求出点F 的坐标，再根据中点坐标公式求解即可． 【满分解答】（1）∵24y ax bx =+-经过点(1,0),(4,0)A B -，4016440a b a b --=⎧∴⎨+-=⎩，13a b =⎧∴⎨=-⎩， ，，，，，，，，，234y x x =--， 对称轴为直线32x =． （2）连接OD ，，，，，234y x x =--经过点C ，(0,4)C ∴-， (10),(4,0)A B -，， 1,4OA OB OC ∴===，又90AOC BOC ∠=∠=︒，11142,44822AOC BOC S S ∆∆∴=⨯⨯==⨯⨯=，4BCD AOC S S ∆∆=， 8BCD S ∆∴=，设2(,34)D x x x --， ，，D 在第四象限，20340x x x ∴>--<，， OCD OBD OCDB S S S ∆∆∴=+四边形=21144(34)22x x x ⨯+⨯-++ =2288x x -++，88=16OBC BCD OCDB S S S ∆∆=+=+四边形，228816x x∴-++=，122x x∴==，(2,6)D∴-．（3）如图2中，当AE为平行四边形的边时，∵DF∥AE，D（2，-6）∴F（1，-6），∴DF=1，∴AE=1，∴E（0，0），或E′（-2，0）．如图3中，当AE，DF是平行四边形的对角线时，∵点D与点F到x轴的距离相等，∴点F 的纵坐标为6， 当y=6时，6=x 2-3x-4， 解得x=-2或5，∴F（-2，6）或（5，6）， 设E （n ，0），则有12222n -+-+=或21522n -++=， 解得n=1或8，∴E（1，0）或（8，0），综上所述，满足条件的点E 的坐标为（0，0）或（1，0）或（8，0）或（-2，0）．【点睛】本题属于二次函数综合题，考查了待定系数法，平行四边形的判定和性质，三角形的面积等知识，解题的关键是学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．10.（2020浦东二模）在平面直角坐标系xOy 中，已知抛物线2y x bx c =-++与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点(0,3)C ，对称轴是直线1x =．（1）求抛物线的表达式；（2）直线MN 平行于x 轴，与抛物线交于M 、N 两点（点M 在点N 的左侧），且34MN AB =，点C 关于直线MN 的对称点为E ，求线段OE 的长；（3）点P 是该抛物线上一点，且在第一象限内，联结CP 、EP ，EP 交线段BC 于点F ，当:1:2CPF CEF S S =△△时，求点P 的坐标．【整体分析】（1）根据抛物线与y 轴交于点(0,3)C 可得出c 的值，然后由对称轴是直线1x =可得出b 的值，从而可求出抛物线的解析式；（2）令y=0得出关于x 的一元二次方程，求出x ，可得出点A 、B 的坐标，从而得到AB 的长，再求出MN 的长，根据抛物线的对称性求出点M 的横坐标，再代入抛物线解析式求出点M 的纵坐标，再根据点的对称可求出OE 的长；（3）过点E 作x 轴的平行线EH ，分别过点F ，P 作EH 的垂线，垂足分别为G ，Q ，则FG ∥PQ ，先证明△EGF ∽△EQP ，可得E E QF EG FG EP PQ ==，设点F 的坐标为（a ，-a+3），则EG=a ，FG=-a+3-12=-a+52，可用含a 的式子表示P 点的坐标，根据P 在抛物线的图象上，可得关于a 的方程，把a 的值代入P 点坐标，可得答案． 【满分解答】解：（1）将点C （0，3）代入2y x bx c =-++得c=3， 又抛物线的对称轴为直线x=1， ∴-2b-=1，解得b=2， ∴抛物线的表达式为y=-x 2+2x+3；（2）如图，令y=0，则-x 2+2x+3=0，解得x 1=-1，x 2=3， ∴点A （-1，0），B （3，0），∴AB=3-（-1）=4， ∵34MN AB =，∴MN=34×4=3， 根据二次函数的对称性，点M 的横坐标为31122-=-， 代入二次函数表达式得，y=22()3211724⎛⎫--⨯-++= ⎪⎝⎭， ∴点M 的坐标为17,24⎛⎫-⎪⎝⎭，。

2020年江苏省中考数学试题分类（4）——二次函数一．二次函数的性质（共4小题）1．（2020•镇江）点P （m ，n ）在以y 轴为对称轴的二次函数y ＝x 2+ax +4的图象上．则m ﹣n 的最大值等于（ ）A ．154B ．4C ．−154D ．−174 2．（2020•无锡）请写出一个函数表达式，使其图象的对称轴为y 轴： ．3．（2020•无锡）二次函数y ＝ax 2﹣3ax +3的图象过点A （6，0），且与y 轴交于点B ，点M 在该抛物线的对称轴上，若△ABM 是以AB 为直角边的直角三角形，则点M 的坐标为 ．4．（2020•淮安）二次函数y ＝﹣x 2﹣2x +3的图象的顶点坐标为 ．二．二次函数图象与几何变换（共2小题）5．（2020•宿迁）将二次函数y ＝（x ﹣1）2+2的图象向上平移3个单位长度，得到的拋物线相应的函数表达式为（ ）A ．y ＝（x +2）2﹣2B ．y ＝（x ﹣4）2+2C ．y ＝（x ﹣1）2﹣1D ．y ＝（x ﹣1）2+56．（2020•南京）下列关于二次函数y ＝﹣（x ﹣m ）2+m 2+1（m 为常数）的结论：①该函数的图象与函数y ＝﹣x 2的图象形状相同；②该函数的图象一定经过点（0，1）；③当x ＞0时，y 随x 的增大而减小；④该函数的图象的顶点在函数y ＝x 2+1的图象上．其中所有正确结论的序号是 ．三．抛物线与x 轴的交点（共3小题）7．（2020•南通）已知抛物线y ＝ax 2+bx +c 经过A （2，0），B （3n ﹣4，y 1），C （5n +6，y 2）三点，对称轴是直线x ＝1．关于x 的方程ax 2+bx +c ＝x 有两个相等的实数根．（1）求抛物线的解析式；（2）若n ＜﹣5，试比较y 1与y 2的大小；（3）若B ，C 两点在直线x ＝1的两侧，且y 1＞y 2，求n 的取值范围．8．（2020•盐城）若二次函数y ＝ax 2+bx +c 的图象与x 轴有两个交点M （x 1，0），N （x 2，0）（0＜x 1＜x 2），且经过点A （0，2）．过点A 的直线l 与x 轴交于点C ，与该函数的图象交于点B （异于点A ）．满足△ACN 是等腰直角三角形，记△AMN 的面积为S 1，△BMN 的面积为S 2，且S 2=52S 1．（1）抛物线的开口方向 （填“上”或“下”）；（2）求直线l 相应的函数表达式；（3）求该二次函数的表达式． 9．（2020•苏州）如图，二次函数y ＝x 2+bx 的图象与x 轴正半轴交于点A ，平行于x 轴的直线l 与该抛物线交于B 、C 两点（点B 位于点C 左侧），与抛物线对称轴交于点D （2，﹣3）．（1）求b 的值；（2）设P 、Q 是x 轴上的点（点P 位于点Q 左侧），四边形PBCQ 为平行四边形．过点P 、Q 分别作x 轴的垂线，与抛物线交于点P '（x 1，y 1）、Q '（x 2，y 2）．若|y 1﹣y 2|＝2，求x 1、x 2的值．四．二次函数的应用（共4小题）10．（2020•连云港）加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率y与加工时间x（单位：min）满足函数表达式y＝﹣0.2x2+1.5x﹣2，则最佳加工时间为min．11．（2020•宿迁）某超市经销一种商品，每千克成本为50元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示：55 60 65 70销售单价x（元/千克）销售量y（千克）70 60 50 40（1）求y（千克）与x（元/千克）之间的函数表达式；（2）为保证某天获得600元的销售利润，则该天的销售单价应定为多少？（3）当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？12．（2020•南京）小明和小丽先后从A地出发沿同一直道去B地．设小丽出发第xmin时，小丽、小明离B 地的距离分别为y1m、y2m．y1与x之间的函数表达式是y1＝﹣180x+2250，y2与x之间的函数表达式是y2＝﹣10x2﹣100x+2000．（1）小丽出发时，小明离A地的距离为m．（2）小丽出发至小明到达B地这段时间内，两人何时相距最近？最近距离是多少？13．（2020•无锡）有一块矩形地块ABCD，AB＝20米，BC＝30米．为美观，拟种植不同的花卉，如图所示，将矩形ABCD分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米．现决定在等腰梯形AEHD 和BCGF中种植甲种花卉；在等腰梯形ABFE和CDHG中种植乙种花卉；在矩形EFGH中种植丙种花卉．甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2，设三种花卉的种植总成本为y元．（1）当x＝5时，求种植总成本y；（2）求种植总成本y与x的函数表达式，并写出自变量x的取值范围；（3）若甲、乙两种花卉的种植面积之差不超过120平方米，求三种花卉的最低种植总成本．五．二次函数综合题（共8小题）14．（2020•镇江）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a ＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点．（1）当a ＝﹣1时，求点N 的坐标及AA AA 的值； （2）随着a 的变化，AA AA 的值是否发生变化？请说明理由；（3）如图②，E 是x 轴上位于点B 右侧的点，BC ＝2BE ，DE 交抛物线于点F ．若FB ＝FE ，求此时的二次函数表达式．15．（2020•宿迁）二次函数y ＝ax 2+bx +3的图象与x 轴交于A （2，0），B （6，0）两点，与y 轴交于点C ，顶点为E ．．（1）求这个二次函数的表达式，并写出点E 的坐标；（2）如图①，D 是该二次函数图象的对称轴上一个动点，当BD 的垂直平分线恰好经过点C 时，求点D 的坐标；（3）如图②，P 是该二次函数图象上的一个动点，连接OP ，取OP 中点Q ，连接QC ，QE ，CE ，当△CEQ 的面积为12时，求点P 的坐标． 16．（2020•徐州）如图，在平面直角坐标系中，函数y ＝﹣ax 2+2ax +3a （a ＞0）的图象交x 轴于点A 、B ，交y 轴于点C ，它的对称轴交x 轴于点E ．过点C 作CD ∥x 轴交抛物线于点D ，连接DE 并延长交y 轴于点F ，交抛物线于点G ．直线AF 交CD 于点H ，交抛物线于点K ，连接HE 、GK ．（1）点E 的坐标为： ；（2）当△HEF 是直角三角形时，求a 的值；（3）HE 与GK 有怎样的位置关系？请说明理由．17．（2020•淮安）如图①，二次函数y＝﹣x2+bx+4的图象与直线l交于A（﹣1，2）、B（3，n）两点．点P 是x轴上的一个动点，过点P作x轴的垂线交直线l于点M，交该二次函数的图象于点N，设点P的横坐标为m．（1）b＝，n＝；（2）若点N在点M的上方，且MN＝3，求m的值；（3）将直线AB向上平移4个单位长度，分别与x轴、y轴交于点C、D（如图②）．①记△NBC的面积为S1，△NAC的面积为S2，是否存在m，使得点N在直线AC的上方，且满足S1﹣S2＝6？若存在，求出m及相应的S1，S2的值；若不存在，请说明理由．②当m＞﹣1时，将线段MA绕点M顺时针旋转90°得到线段MF，连接FB、FC、OA．若∠FBA+∠AOD﹣∠BFC＝45°，直接写出直线OF与该二次函数图象交点的横坐标．18．（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．（1）填空：b＝；（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD＝∠ACB，求点P的坐标；（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．19．（2020•泰州）如图，二次函数y 1＝a （x ﹣m ）2+n ，y 2＝6ax 2+n （a ＜0，m ＞0，n ＞0）的图象分别为C 1、C 2，C 1交y 轴于点P ，点A 在C 1上，且位于y 轴右侧，直线P A 与C 2在y 轴左侧的交点为B ．（1）若P 点的坐标为（0，2），C 1的顶点坐标为（2，4），求a 的值；（2）设直线P A 与y 轴所夹的角为α．①当α＝45°，且A 为C 1的顶点时，求am 的值；②若α＝90°，试说明：当a 、m 、n 各自取不同的值时，AA AA 的值不变；（3）若P A ＝2PB ，试判断点A 是否为C 1的顶点？请说明理由．20．（2020•连云港）在平面直角坐标系xOy 中，把与x 轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L 1：y =12x 2−32x ﹣2的顶点为D ，交x 轴于点A 、B （点A 在点B 左侧），交y 轴于点C ．抛物线L 2与L 1是“共根抛物线”，其顶点为P ．（1）若抛物线L 2经过点（2，﹣12），求L 2对应的函数表达式；（2）当BP ﹣CP 的值最大时，求点P 的坐标；（3）设点Q 是抛物线L 1上的一个动点，且位于其对称轴的右侧．若△DPQ 与△ABC 相似，求其“共根抛物线”L 2的顶点P 的坐标． 21．（2020•无锡）在平面直角坐标系中，O 为坐标原点，直线OA 交二次函数y =14x 2的图象于点A ，∠AOB＝90°，点B 在该二次函数的图象上，设过点（0，m ）（其中m ＞0）且平行于x 轴的直线交直线OA 于点M ，交直线OB 于点N ，以线段OM 、ON 为邻边作矩形OMPN ．（1）若点A 的横坐标为8．①用含m的代数式表示M的坐标；②点P能否落在该二次函数的图象上？若能，求出m的值；若不能，请说明理由．（2）当m＝2时，若点P恰好落在该二次函数的图象上，请直接写出此时满足条件的所有直线OA的函数表达式．2020年江苏省中考数学试题分类（4）——二次函数参考答案与试题解析一．二次函数的性质（共4小题）1．【解答】解：∵点P （m ，n ）在以y 轴为对称轴的二次函数y ＝x 2+ax +4的图象上，∴a ＝0，∴n ＝m 2+4，∴m ﹣n ＝m ﹣（m 2+4）＝﹣m 2+m ﹣4＝﹣（m −12）2−154，∴当m =12时，m ﹣n 取得最大值，此时m ﹣n =−154，故选：C ．2．【解答】解：∵图象的对称轴是y 轴，∴函数表达式y ＝x 2（答案不唯一），故答案为：y ＝x 2（答案不唯一）．3．【解答】解：∵抛物线的对称轴为x =−122×(−16)=32， 设点M 的坐标为：（32，m ），当∠ABM ＝90°，过B 作BD 垂直对称轴于D ，则∠1＝∠2，∴tan ∠2＝tan ∠1=63=2， ∴AA AA =2，∴DM ＝3， ∴M （32，6），当∠M ′AB ＝90°时，∴tan ∠3=A′A AA =tan ∠1=63=2， ∴M ′N ＝9， ∴M ′（32，﹣9），综上所述，点M 的坐标为（32，﹣9）或（32，6）．故答案为：（32，﹣9）或（32，6）． 4．【解答】解：∵y ＝﹣x 2﹣2x +3＝﹣（x 2+2x +1﹣1）+3＝﹣（x +1）2+4，∴顶点坐标为（﹣1，4）．故答案为：（﹣1，4）．二．二次函数图象与几何变换（共2小题）5．【解答】解：由“上加下减”的原则可知，将二次函数y ＝（x ﹣1）2+2的图象向上平移3个单位长度，所得抛物线的解析式为：y ＝（x ﹣1）2+2+3，即y ＝（x ﹣1）2+5；故选：D ．6．【解答】解：①∵二次函数y ＝﹣（x ﹣m ）2+m +1（m 为常数）与函数y ＝﹣x 2的二次项系数相同， ∴该函数的图象与函数y ＝﹣x 2的图象形状相同，故结论①正确；②∵在函数y ＝﹣（x ﹣m ）2+m 2+1中，令x ＝0，则y ＝﹣m 2+m 2+1＝1，∴该函数的图象一定经过点（0，1），故结论②正确；③∵y ＝﹣（x ﹣m ）2+m 2+1，∴抛物线开口向下，对称轴为直线x ＝m ，当x ＞m 时，y 随x 的增大而减小，故结论③错误；④∵抛物线开口向下，当x ＝m 时，函数y 有最大值m 2+1，∴该函数的图象的顶点在函数y ＝x 2+1的图象上．故结论④正确，故答案为①②④．三．抛物线与x 轴的交点（共3小题）7．【解答】解：（1）∵抛物线y ＝ax 2+bx +c 经过A （2，0），∴0＝4a +2b +c ①，∵对称轴是直线x ＝1，∴−A 2A =1②， ∵关于x 的方程ax 2+bx +c ＝x 有两个相等的实数根，∴△＝（b ﹣1）2﹣4ac ＝0③，由①②③可得：{A =−12A =1A =0，∴抛物线的解析式为y =−12x 2+x ；（2）∵n ＜﹣5，∴3n ﹣4＜﹣19，5n +6＜﹣19∴点B ，点C 在对称轴直线x ＝1的左侧，∵抛物线y =−12x 2+x ，∴−12＜0，即y 随x 的增大而增大，∵（3n ﹣4）﹣（5n +6）＝﹣2n ﹣10＝﹣2（n +5）＞0，∴3n ﹣4＞5n +6，∴y 1＞y 2；（3）若点B 在对称轴直线x ＝1的左侧，点C 在对称轴直线x ＝1的右侧时，由题意可得{3A −4＜15A +6＞11−(3A −4)＜5A +6−1， ∴0＜n ＜53， 若点C 在对称轴直线x ＝1的左侧，点B 在对称轴直线x ＝1的右侧时，由题意可得：{3A −4＞15A +6＜13A −4−1＜1−(5A +6)，∴不等式组无解，综上所述：0＜n ＜53．8．【解答】解：（1）如图，如二次函数y ＝ax 2+bx +c 的图象与x 轴有两个交点M （x 1，0），N （x 2，0）（0＜x 1＜x 2），且经过点A （0，2）．∴y ＝ax 2+bx +2，令y ＝0，则ax 2+bx +2＝0，∵0＜x 1＜x 2，∴2A ＞0，∴a ＞0，∴抛物线开口向上，故答案为：上；（2）①若∠ACN ＝90°，则C 与O 重合，直线l 与抛物线交于A 点，因为直线l 与该函数的图象交于点B （异于点A ），所以不合题意，舍去；②若∠ANC ＝90°，则C 在x 轴的下方，与题意不符，舍去；③若∠CAN ＝90°，则∠ACN ＝∠ANC ＝45°，AO ＝CO ＝NO ＝2，∴C （﹣2，0），N （2，0），设直线l 为y ＝kx +b ，将A （0，2）C （﹣2，0）代入得{A =2−2A +A =0， 解得{A =1A =2， ∴直线l 相应的函数表达式为y ＝x +2；（3）过B 点作BH ⊥x 轴于H ，S 1=12AA ⋅AA ，S 2=12AA ⋅AA ，∵S 2=52S 1， ∴BH =52OA ， ∵OA ＝2，∴BH ＝5，即B 点的纵坐标为5，代入y ＝x +2中，得x ＝3，∴B （3，5），将A 、B 、N 三点的坐标代入y ＝ax 2+bx +c 得{A =24A +2A +A =09A +3A +A =5，解得{A =2A =−5A =2，∴抛物线的解析式为y ＝2x 2﹣5x +2．9．【解答】解：（1）直线与抛物线的对称轴交于点D （2，﹣3），故抛物线的对称轴为x ＝2，即−12b ＝2，解得：b ＝﹣4，（2）∵b ＝﹣4∴抛物线的表达式为：y ＝x 2﹣4x ；把y ＝﹣3代入y ＝x 2﹣4x 并解得x ＝1或3，故点B 、C 的坐标分别为（1，﹣3）、（3，﹣3），则BC ＝2，∵四边形PBCQ 为平行四边形，∴PQ ＝BC ＝2，故x 2﹣x 1＝2，又∵y 1＝x 12﹣4x 1，y 2＝x 22﹣4x 2，|y 1﹣y 2|＝2，故|（x 12﹣4x 1）﹣（x 22﹣4x 2）|＝2，|x 1+x 2﹣4|＝1．∴x 1+x 2＝5或x 1+x 2＝3，由{A 2−A 1=2A 1+A 2=5，解得{A 1=32A 2=72； 由{A 2−A 1=2A 1+A 2=3，解得{A 1=12A 2=52． 四．二次函数的应用（共4小题）10．【解答】解：根据题意：y ＝﹣0.2x 2+1.5x ﹣2，当x =−1.52×(−0.2)=3.75时，y 取得最大值， 则最佳加工时间为3.75min ．故答案为：3.75．11．【解答】解：（1）设y 与x 之间的函数表达式为y ＝kx +b （k ≠0），将表中数据（55，70）、（60，60）代入得：{55A +A =7060A +A =60， 解得：{A =−2A =180． ∴y 与x 之间的函数表达式为y ＝﹣2x +180．（2）由题意得：（x ﹣50）（﹣2x +180）＝600，整理得：x 2﹣140x +4800＝0，解得x 1＝60，x 2＝80．答：为保证某天获得600元的销售利润，则该天的销售单价应定为60元/千克或80元/千克．（3）设当天的销售利润为w 元，则：w ＝（x ﹣50）（﹣2x +180）＝﹣2（x ﹣70）2+800，∵﹣2＜0，∴当x ＝70时，w 最大值＝800．答：当销售单价定为70元/千克时，才能使当天的销售利润最大，最大利润是800元．12．【解答】解：（1）∵y 1＝﹣180x +2250，y 2＝﹣10x 2﹣100x +2000，∴当x ＝0时，y 1＝2250，y 2＝2000，∴小丽出发时，小明离A 地的距离为2250﹣2000＝250（m ），故答案为：250；（2）设小丽出发第xmin 时，两人相距sm ，则s ＝（﹣180x +2250）﹣（﹣10x 2﹣100x +2000）＝10x 2﹣80x +250＝10（x ﹣4）2+90，∴当x ＝4时，s 取得最小值，此时s ＝90，答：小丽出发第4min 时，两人相距最近，最近距离是90m ．13．【解答】解：（1）当x ＝5时，EF ＝20﹣2x ＝10，EH ＝30﹣2x ＝20，y ＝2×12（EH +AD ）×20x +2×12（GH +CD ）×x ×60+EF •EH ×40＝（20+30）×5×20+（10+20）×5×60+20×10×40＝22000；（2）EF ＝（20﹣2x ）米，EH ＝（30﹣2x ）米，参考（1），由题意得：y ＝（30+30﹣2x ）•x •20+（20+20﹣2x ）•x •60+（30﹣2x ）（20﹣2x ）•40＝﹣400x +24000（0＜x ＜10）；（3）S 甲＝2×12（EH +AD ）×x ＝（30﹣2x +30）x ＝﹣2x 2+60x ， 同理S 乙＝﹣2x 2+40x ，∵甲、乙两种花卉的种植面积之差不超过120米2，∴﹣2x 2+60x ﹣（﹣2x 2+40x ）≤120，解得：x ≤6，故0＜x ≤6，而y ＝﹣400x +24000随x 的增大而减小，故当x ＝6时，y 的最小值为21600，即三种花卉的最低种植总成本为21600元．五．二次函数综合题（共8小题）14．【解答】解：（1）分别过点M 、N 作MG ⊥CD 于点E ，NT ⊥DC 于点T ，∵MG ∥TN ∥x 轴，∴△DMG ∽△DAC ，△DCB ∽△DTN ，∴AA AA =AA AA ，AA AA =AA AA ，∵a ＝﹣1，则y ＝﹣x 2+2x +c ，将M （﹣1，1）代入上式并解得：c ＝4，∴抛物线的表达式为：y ＝﹣x 2+2x +4，则点D （1，5），N （4，﹣4），则MG ＝2，DG ＝4，DC ＝5，TN ＝3，DT ＝9，∴2AA =45，AA 3=59，解得：AC =52，BC =53， ∴AA AA =32；（2）不变，理由：第（2）问有错误MG ＝2，DG ＝4a∵y ＝ax 2﹣2ax +c 过点M （﹣1，1），则a +2a +c ＝1，解得：c ＝1﹣3a ，∴y ＝ax 2﹣2ax +（1﹣3a ），∴点D （1，1﹣4a ），N （4，1+5a ），∴MG ＝2，DG ＝4a ，DC ＝1﹣4a ，FN ＝3，DF ＝﹣9a ，由（1）的结论得：AC =1−4A −2A ，BC =1−4A −3A ，∴AA AA =32；（3）过点F 作FH ⊥x 轴于点H ，则FH ∥l ，则△FHE ∽△DCE ，∵FB ＝FE ，FH ⊥BE ，∴BH ＝HE ，∵BC ＝2BE ，则CE ＝6HE ，∵CD ＝1﹣4a ，∴FH =1−4A 6， ∵BC =4A −13A ， ∴CH =54×4A −13A =20A −512A ，∴F （53−512A +1，16−23a ）， 将点F 的坐标代入y ＝ax 2﹣2ax +（1﹣3a ）＝a （x +1）（x ﹣3）+1得： 16−23a ＝a （53−512A +1+1）（53−512A +1﹣3）+1，解得：a =−54或14（舍弃）， 经检验a =−54，故y =−54x 2+52x +194． 15．【解答】解：（1）将A （2，0），B （6，0）代入y ＝ax 2+bx +3， 得{4A +2A +3=036A +6A +3=0， 解得{A =14A =−2 ∴二次函数的解析式为y =14A 2−2x +3．∵y =14A 2−2A +3=14(A −4)2−1，∴E （4，﹣1）．（2）如图1，图2，连接CB ，CD ，由点C 在线段BD 的垂直平分线CN 上，得CB ＝CD ．设D （4，m ），∵C （0，3），由勾股定理可得：42+（m ﹣3）2＝62+32．解得m ＝3±√29．∴满足条件的点D 的坐标为（4，3+√29）或(4，3−√29)．（3）如图3，设CQ 交抛物线的对称轴于点M ，设P （n ，14A 2−2n +3），则Q （12A ，18A 2−A +32）， 设直线CQ 的解析式为y ＝kx +3，则18A 2−A +32=12nk +3． 解得k =14A −2−3A ，于是CQ ：y ＝（14A −2−3A ）x +3，当x ＝4时，y ＝4（14A −2−3A ）+3＝n ﹣5−12A， ∴M （4，n ﹣5−12A ），ME ＝n ﹣4−12A ．∵S △CQE ＝S △CEM +S △QEM =12×12A ⋅AA =12⋅12A ⋅(A −4−12A )=12． ∴n 2﹣4n ﹣60＝0，解得n ＝10或n ＝﹣6，当n ＝10时，P （10，8），当n ＝﹣6时，P （﹣6，24）．综合以上可得，满足条件的点P 的坐标为（10，8）或（﹣6，24）．16．【解答】解：（1）对于抛物线y ＝﹣ax 2+2ax +3a ，对称轴x =−2A −2A=1， ∴E （1，0），故答案为（1，0）．（2）如图，连接EC ．对于抛物线y ＝﹣ax 2+2ax +3a ，令x ＝0，得到y ＝3a ，令y ＝0，﹣ax 2+2ax +3a ＝0，解得x ＝﹣1或3，∴A （﹣1，0），B （3，0），C （0，3a ），∵C ，D 关于对称轴对称，∴D （2，3a ），CD ＝2，EC ＝DE ，当∠HEF ＝90°时，∵ED ＝EC ，∴∠ECD ＝∠EDC ，∵∠DCF ＝90°，∴∠CFD +∠EDC ＝90°，∠ECF +∠ECD ＝90°，∴∠ECF ＝∠EFC ，∴EC ＝EF ＝DE ，∵EA ∥DH ，∴F A ＝AH ，∴AE =12DH ，∵AE ＝2，∴DH ＝4，∵HE ⊥DFEF ＝ED ，∴FH ＝DH ＝4，在Rt △CFH 中，则有42＝22+（6a ）2，解得a =√33或−√33（不符合题意舍弃），∴a =√33．当∠HFE ＝90°时，∵OA ＝OE ，FO ⊥AE ，∴F A ＝FE ，∴OF ＝OA ＝OE ＝1，∴3a ＝1，∴a =13， 综上所述，满足条件的a 的值为√33或13．（3）结论：EH ∥GK ．理由：由题意A （﹣1，0），F （0，﹣3a ），D （2，3a ），H （﹣2，3a ），E （1，0），∴直线AF 的解析式y ＝﹣3ax ﹣3a ，直线DF 的解析式为y ＝3ax ﹣3a ，由{A =−3AA −3A A =−AA 2+2AA +3A ，解得{A =−1A =0或{A =6A =−21A ， ∴K （6，﹣21a ），由{A =3AA −3A A =−AA 2+2AA +3A ，解得{A =2A =3A 或{A =−3A =−12A ， ∴G （﹣3，﹣12a ），∴直线HE 的解析式为y ＝﹣ax +a ，直线GK 的解析式为y ＝﹣ax ﹣15a ，∵k 相同，a ≠﹣15a ，∴HE ∥GK ．17．【解答】解：（1）将点A （﹣1，2）代入二次函数y ＝﹣x 2+bx +4中，得﹣1﹣b +4＝2，∴b ＝1，∴二次函数的解析式为y ＝﹣x 2+x +4，将点B （3，n ）代入二次函数y ＝﹣x 2+x +4中，得n ＝﹣9+3+4＝﹣2，故答案为：1，﹣2；（2）设直线AB 的解析式为y ＝kx +a ，由（1）知，点B （3，﹣2），∵A （﹣1，2），∴{−A +A =23A +A =−2， ∴{A =−1A =1， ∴直线AB 的解析式为y ＝﹣x +1，由（1）知，二次函数的解析式为y ＝﹣x 2+x +4，∵点P （m ，0），∴M （m ，﹣m +1），N （m ，﹣m 2+m +4），∵点N 在点M 的上方，且MN ＝3，∴﹣m 2+m +4﹣（﹣m +1）＝3，∴m ＝0或m ＝2；（3）①如图1，由（2）知，直线AB 的解析式为y ＝﹣x +1，∴直线CD 的解析式为y ＝﹣x +1+4＝﹣x +5，令y ＝0，则﹣x +5＝0，∴x ＝5，∴C （5，0），∵A （﹣1，2），B （3，﹣2），∴直线AC 的解析式为y =−13x +53，直线BC 的解析式为y ＝x ﹣5，过点N 作y 轴的平行线交AC 于K ，交BC 于H ，∵点P （m ，0），∴N （m ，﹣m 2+m +4），K （m ，−13m +53），H （m ，m ﹣5），∴NK ＝﹣m 2+m +4+13m −53=−m 2+43m +73，NH ＝﹣m 2+9，∴S 2＝S △NAC =12NK ×（x C ﹣x A ）=12（﹣m 2+43m +73）×6＝﹣3m 2+4m +7，S 1＝S △NBC =12NH ×（x C ﹣x B ）＝﹣m 2+9，∵S 1﹣S 2＝6，∴﹣m 2+9﹣（﹣3m 2+4m +7）＝6，∴m ＝1+√3（由于点N 在直线AC 上方，所以，舍去）或m ＝1−√3；∴S 2＝﹣3m 2+4m +7＝﹣3（1−√3）2+4（1−√3）+7＝2√3−1，S 1＝﹣m 2+9＝﹣（1−√3）2+9＝2√3+5；②如图2，记直线AB 与x 轴，y 轴的交点为I ，L ，由（2）知，直线AB 的解析式为y ＝﹣x +1，∴I （1，0），L （0，1），∴OL ＝OI ，∴∠ALD ＝∠OLI ＝45°，∴∠AOD +∠OAB ＝45°，过点B 作BG ∥OA ，∴∠ABG ＝∠OAB ，∴∠AOD +∠ABG ＝45°，∵∠FBA ＝∠ABG +∠FBG ，∠FBA +∠AOD ﹣∠BFC ＝45°，∴∠ABG +∠FBG +∠AOD ﹣∠BFC ＝45°，∴∠FBG ＝∠BFC ，∴BG ∥CF ，∴OA ∥CF ，∵A （﹣1，2），∴直线OA 的解析式为y ＝﹣2x ，∵C （5，0），∴直线CF 的解析式为y ＝﹣2x +10，过点A ，F 分别作过点M 平行于x 轴的直线的垂线，交于点Q ，S ，由旋转知，AM ＝MF ，∠AMF ＝90°，∴△AMF 是等腰直角三角形，∴∠F AM ＝45°，∵∠AIO ＝45°，∴∠F AM ＝∠AIO ，∴AF ∥x 轴，∴点F 的纵坐标为2，∴F （4，2），∴直线OF 的解析式为y =12x ①，∵二次函数的解析式为y ＝﹣x 2+x +4②， 联立①②解得，{A =1+√654A =1+√658或{A =1−√654A =1−√658， ∴直线OF 与该二次函数图象交点的横坐标为1+√654或1−√654．18．【解答】解：（1）∵抛物线y＝x2+bx+3的图象过点C（1，0），∴0＝1+b+3，∴b＝﹣4，故答案为：﹣4；（2）∵b＝﹣4，∴抛物线解析式为y＝x2﹣4x+3∵抛物线y＝x2﹣4x+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，∴点A（0，3），3＝x2﹣4x+3，∴x1＝0（舍去），x2＝4，∴点B（4，3），∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴顶点D坐标（2，﹣1），如图1，当点Q在点D上方时，过点C作CE⊥AB于E，设BD与x轴交于点F，∵点A（0，3），点B（4，3），点C（1，0），CE⊥AB，∴点E（1，3），CE＝BE＝3，AE＝1，∴∠EBC＝∠ECB＝45°，tan∠ACE=AAAA=13，∴∠BCF＝45°，∵点B（4，3），点C（1，0），点D（2，﹣1），∴BC=√9+9=3√2，CD=√1+1=√2，BD=√(4−2)2+(3+1)2=2√5，∵BC2+CD2＝20＝BD2，∴∠BCD＝90°，∴tan ∠DBC =AA AA =√23√2=13=tan ∠ACE ， ∴∠ACE ＝∠DBC ，∴∠ACE +∠ECB ＝∠DBC +∠BCF ，∴∠ACB ＝∠CFD ，又∵∠CQD ＝∠ACB ，∴点F 与点Q 重合，∴点P 是直线CF 与抛物线的交点，∴0＝x 2﹣4x +3，∴x 1＝1，x 2＝3，∴点P （3，0）；当点Q 在点D 下方上，过点C 作CH ⊥DB 于H ，在线段BH 的延长线上截取HF ＝QH ，连接CQ 交抛物线于点P ，∵CH ⊥DB ，HF ＝QH ，∴CF ＝CQ ，∴∠CFD ＝∠CQD ，∴∠CQD ＝∠ACB ，∵CH ⊥BD ，∵点B （4，3），点D （2，﹣1），∴直线BD 解析式为：y ＝2x ﹣5，∴点F （52，0）， ∴直线CH 解析式为：y =−12x +12， ∴{A =−12A +12A =2A −5，解得{A =115A =−35， ∴点H 坐标为（115，−35）， ∵FH ＝QH ，∴点Q （1910，−65）， ∴直线CQ 解析式为：y =−43x +43， 联立方程组{A =−43A +43A =A 2−4A +3，解得：{A 1=1A 1=0或{A 2=53A 2=−89，∴点P （53，−89）； 综上所述：点P 的坐标为（3，0）或（53，−89）；（3）如图，设直线AC 与BD 的交点为N ，作CH ⊥BD 于H ，过点N 作MN ⊥x 轴，过点E 作EM ⊥MN ，连接CG ，GF ，∵点A （0，3），点C （1，0），∴直线AC 解析式为：y ＝﹣3x +3，∴{A =−3A +3A =2A −5， ∴{A =85A =−95， ∴点N 坐标为（85，−95），∵点H 坐标为（115，−35）， ∴CH 2＝（115−1）2+（35）2=95，HN 2＝（115−85）2+（−35+95）2=95， ∴CH ＝HN ，∴∠CNH ＝45°，∵点E 关于直线BD 对称的点为F ，∴EN ＝NF ，∠ENB ＝∠FNB ＝45°，∴∠ENF ＝90°，∴∠ENM +∠FNM ＝90°，又∵∠ENM +∠MEN ＝90°，∴∠MEN ＝∠FNM ，∴△EMN ≌△NKF （AAS ）∴EM ＝NK =95，MN ＝KF ，∴点E 的横坐标为−15，∴点E （−15，185）， ∴MN =275=KF ，∴CF =85+275−1＝6， ∵点F 关于直线BC 对称的点为G ，∴FC ＝CG ＝6，∠BCF ＝∠GCB ＝45°，∴∠GCF ＝90°，∴点G （1，6），∴AG =√12+(6−3)2=√10．19．【解答】解：（1）由题意m ＝2，n ＝4，∴y 1＝a （x ﹣2）2+4，把（0，2）代入得到a =−12．（2）①如图1中，过点A 作AN ⊥x 轴于N ，过点P 作PM ⊥AN 于M ． ∵y 1＝a （x ﹣m ）2+n ＝ax 2﹣2amx +am 2+n ，∴P （0，am 2+n ），∵A （m ，n ），∴PM ＝m ，AN ＝n ，∵∠APM ＝45°，∴AM ＝PM ＝m ，∴m +am 2+n ＝n ，∵m ＞0，∴am ＝﹣1．②如图2中，由题意AB ⊥y 轴， ∵P （0，am 2+n ），当y ＝am 2+n 时，am 2+n ＝6ax 2+n ，解得x ＝±√66m ， ∴B （−√66m ，am 2+n ），∴PB =√66m ，∵AP ＝2m ，∴AA AA =√66A =2√6．（3）如图3中，过点A 作AH ⊥x 轴于H ，过点P 作PK ⊥AH 于K ，过点B 作BE ⊥KP 交KP 的延长线于E ．设B （b ，6ab 2+n ），∵P A ＝2PB ，∴点A 的横坐标为﹣2b ，∴A [﹣2b ，a （﹣2b ﹣m ）2+n ]，∵BE ∥AK ， ∴AAAA =AAAA =12， ∴AK ＝2BE ，∴a （﹣2b ﹣m ）2+n ﹣am 2﹣n ＝2（am 2+n ﹣6ab 2﹣n ），整理得：m 2﹣2bm ﹣8b 2＝0，∴（m ﹣4b ）（m +2b ）＝0，∵m ﹣4b ＞0，∴m +2b ＝0，∴m ＝﹣2b ，∴A （m ，n ），∴点A 是抛物线C 1的顶点．20．【解答】解：（1）当y ＝0时，12x 2−32x ﹣2＝0，解得x ＝﹣1或4，∴A （﹣1，0），B （4，0），C （0，﹣2），由题意设抛物线L 2的解析式为y ＝a （x +1）（x ﹣4），把（2，﹣12）代入y ＝a （x +1）（x ﹣4），﹣12＝﹣6a ，解得a ＝2，∴抛物线的解析式为y ＝2（x +1）（x ﹣4）＝2x 2﹣6x ﹣8．（2）∵抛物线L 2与L 1是“共根抛物线”，A （﹣1，0），B （4，0），∴抛物线L 1，L 2的对称轴是直线x =32， ∴点P 在直线x =32上，∴BP ＝AP ，如图1中，当A ，C ，P 共线时，BP ﹣PC 的值最大，此时点P 为直线AC 与直线x =32的交点，∵直线AC 的解析式为y ＝﹣2x ﹣2，∴P （32，﹣5）（3）由题意，AB ＝5，CB ＝2√5，CA =√5，∴AB 2＝BC 2+AC 2，∴∠ACB ＝90°，CB ＝2CA ，∵y =12x 2−32x ﹣2=12（x −32）2−258，∴顶点D （32，−258）， 由题意，∠PDQ 不可能是直角，第一种情形：当∠DPQ ＝90°时，①如图3﹣1中，当△QDP ∽△ABC 时，AA AA =AA AA =12， 设Q （x ，12x 2−32x ﹣2），则P （32，12x 2−32x ﹣2），∴DP =12x 2−32x ﹣2﹣（−258）=12x 2−32x +98，QP ＝x −32， ∵PD ＝2QP ，∴2x ﹣3=12x 2−32x +98，解得x =112或32（舍弃）， ∴P （32，398）．②如图3﹣2中，当△DQP ∽△ABC 时，同法可得PQ ＝2PD ，x −32=x 2﹣3x +94，解得x =52或32（舍弃）， ∴P （32，−218）． 第二种情形：当∠DQP ＝90°．①如图3﹣3中，当△PDQ ∽△ABC 时，AA AA =AA AA =12， 过点Q 作QM ⊥PD 于M ．则△QDM ∽△PDQ ，∴AA AA =AA AA =12，由图3﹣3可知，M （32，398），Q （112，398）， ∴MD ＝8，MQ ＝4，∴DQ ＝4√5，由AA AA =AA AA ，可得PD ＝10， ∵D （32，−258） ∴P （32，558）．②当△DPQ ∽△ABC 时，过点Q 作QM ⊥PD 于M ．同法可得M （32，−218），Q （52，−218）， ∴DM =12，QM ＝1，QD =√52，由AA AA =AA AA ，可得PD =52， ∴P （32，−58）． 综上所述：P 点坐标为（32，398）或（32，−218）或（32，558）或（32，−58）． 21．【解答】解：（1）①∵点A 在y =14x 2的图象上，横坐标为8， ∴A （8，16），∴直线OA 的解析式为y ＝2x ，∵点M 的纵坐标为m ，∴M （12m ，m ）．②假设能在抛物线上，连接OP ．∵∠AOB ＝90°，∴直线OB 的解析式为y =−12x ，∵点N 在直线OB 上，纵坐标为m ，∴N （﹣2m ，m ），∴MN 的中点的坐标为（−34m ，m ），∴P （−32m ，2m ），把点P 坐标代入抛物线的解析式得到m =329．（2）①当点A 在y 轴的右侧时，设A （a ，14a 2），∴直线OA 的解析式为y =14ax ， ∴M （8A，2），∵OB ⊥OA ， ∴直线OB 的解析式为y =−4A x ，可得N （−A 2，2），∴P （8A −A 2，4），代入抛物线的解析式得到，8A −A 2=±4，解得，a ＝4√2±4，∴直线OA 的解析式为y ＝（√2±1）x ．②当点A 在y 轴的左侧时，即为①中点B 的位置，∴直线OA的解析式为y=−4A x＝﹣（√2±1）x，综上所述，满足条件的直线OA的解析式为y＝（√2±1）x或y＝﹣（√2±1）x．。

2018-2020年上海市中考数学各地区模拟试题分类（一）——《二次函数》一．选择题1．（2019•闵行区一模）已知二次函数y＝ax2+bx+c的图象如图所示，那么根据图象，下列判断中不正确的是（）A．a＜0 B．b＞0 C．c＞0 D．abc＞0 2．（2019•金山区一模）已知抛物线y＝ax2+bx+c（a≠0）如图所示，那么a、b、c的取值范围是（）A．a＜0、b＞0、c＞0 B．a＜0、b＜0、c＞0C．a＜0、b＞0、c＜0 D．a＜0、b＜0、c＜03．（2019•浦东新区一模）已知二次函数y＝﹣（x+3）2，那么这个二次函数的图象有（）A．最高点（3，0）B．最高点（﹣3，0）C．最低点（3，0）D．最低点（﹣3，0）4．（2019•闵行区一模）将二次函数y＝2（x﹣2）2的图象向左平移1个单位，再向下平移3个单位后所得图象的函数解析式为（）A．y＝2（x﹣2）2﹣4 B．y＝2（x﹣1）2+3C．y＝2（x﹣1）2﹣3 D．y＝2x2﹣35．（2019•浦东新区一模）如果将抛物线y＝x2+4x+1平移，使它与抛物线y＝x2+1重合，那么平移的方式可以是（）A．向左平移2个单位，向上平移4个单位B．向左平移2个单位，向下平移4个单位C．向右平移2个单位，向上平移4个单位D．向右平移2个单位，向下平移4个单位6．（2019•嘉定区一模）下列函数中，是二次函数的是（）A．y＝2x+1 B．y＝（x﹣1）2﹣x2C．y＝1﹣x2D．y＝7．（2019•金山区一模）下列函数是二次函数的是（）A．y＝x B．y＝C．y＝x﹣2+x2D．y＝8．（2019•长宁区一模）抛物线y＝2（x+2）2﹣3的顶点坐标是（）A．（2，﹣3）B．（﹣2，﹣3）C．（﹣2，3）D．（2，3）9．（2019•黄浦区一模）在平面直角坐标系中，如果把抛物线y＝﹣2x2向上平移1个单位，那么得到的抛物线的表达式是（）A．y＝﹣2（x+1）2B．y＝﹣2（x﹣1）2C．y＝﹣2x2+1 D．y＝﹣2x2﹣1 10．（2019•杨浦区模拟）二次函数的复习课中，夏老师给出关于x的函数y＝2kx2﹣（4k+1）x﹣k+1（k为实数）．夏老师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上．学生独立思考后，黑板上出现了一些结论．夏老师作为活动一员，又补充了一些结论，并从中选择了如下四条：①存在函数，其图象经过点（1，0）；②存在函数，该函数的函数值y始终随x的增大而减小；③函数图象有可能经过两个象限；④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数．上述结论中正确个数为（）A．1个B．2个C．3个D．4个11．（2018•虹口区二模）如果将抛物线y＝x2向左平移1个单位，那么所得新抛物线的表达式是（）A．y＝x2+1 B．y＝x2﹣1 C．y＝（x+1）2D．y＝（x﹣1）2．12．（2018•金山区二模）如果将抛物线y＝﹣2x2向上平移1个单位，那么所得新抛物线的表达式是（）A．y＝﹣2（x+1）2B．y＝﹣2（x﹣1）2C．y＝﹣2x2﹣1 D．y＝﹣2x2+1 13．（2018•浦东新区模拟）将抛物线y＝（x﹣1）2向左平移2个单位，所得抛物线的表达式为（）A．y＝（x+1）2B．y＝（x﹣3）2C．y＝（x﹣1）2+2 D．y＝（x﹣1）2﹣214．（2018•金山区一模）将抛物线y＝﹣（x+1）2+4平移，使平移后所得抛物线经过原点，那么平移的过程为（）A．向下平移3个单位B．向上平移3个单位C．向左平移4个单位D．向右平移4个单位15．（2018•黄浦区一模）已知二次函数y＝ax2+bx+c的图象大致如图所示，则下列关系式中成立的是（）A．a＞0 B．b＜0 C．c＜0 D．b+2a＞0二．填空题16．（2020•静安区一模）某商场四月份的营业额是200万元，如果该商场第二季度每个月营业额的增长率相同，都为x（x＞0），六月份的营业额为y万元，那么y关于x的函数解析式是．17．（2020•金山区一模）如果一条抛物线经过点A（2，5），B（﹣3，5），那么它的对称轴是直线．18．（2020•静安区一模）已知二次函数y＝a2x2+8a2x+a（a是常数，a≠0），当自变量x分别取﹣6、﹣4时，对应的函数值分别为y1、y2，那么y1、y2的大小关系是：y1y2（填“＞”、“＜”或“＝”）．19．（2020•浦东新区一模）将抛物线y＝﹣3x2向下平移4个单位，那么平移后所得新抛物线的表达式为．20．（2020•浦东新区一模）二次函数y＝﹣2（x+1）2的图象在对称轴左侧的部分是．（填“上升”或“下降”）21．（2020•青浦区一模）如果抛物线y＝ax2﹣1的顶点是它的最低点，那么a的取值范围是．22．（2020•金山区一模）抛物线y＝2x2﹣1在y轴左侧的部分是．（填“上升”或“下降”）23．（2020•松江区一模）在直角坐标平面中，将抛物线y＝2（x+1）2先向上平移1个单位，再向右平移1个单位，那么平移后的抛物线表达式是．24．（2020•嘉定区一模）将抛物线y＝x2+4x+5向右平移2个单位后，所得抛物线的表达式为．三．解答题25．（2020•金山区二模）在平面直角坐标系xOy中（如图），已知抛物线y＝﹣x2+bx+c经过点A（3，0）和B（0，3），其顶点为C．（1）求抛物线的解析式和顶点C的坐标；（2）我们把坐标为（n，m）的点叫做坐标为（m，n）的点的反射点，已知点M在这条抛物线上，它的反射点在抛物线的对称轴上，求点M的坐标；（3）点P是抛物线在第一象限部分上的一点，如果∠POA＝∠ACB，求点P的坐标．26．（2020•徐汇区二模）如图，抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和B，与y轴交于点C，顶点为点D．（1）求抛物线的表达式、点B和点D的坐标；（2）将抛物线y＝ax2﹣2ax+3向右平移后所得新抛物线经过原点O，点B、D的对应点分别是点B'，D'，联结B'C，B'D'，CD'，求△CB'D'的面积．27．（2020•闵行区一模）如图，已知一个抛物线经过A（0，1），B（1，3），C（﹣1，1）三点．（1）求这个抛物线的表达式及其顶点D的坐标；（2）联结AB、BC、CA，求tan∠ABC的值；（3）如果点E在该抛物线的对称轴上，且以点A、B、C、E为顶点的四边形是梯形，直接写出点E的坐标．28．（2020•虹口区一模）在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0）、B两点，与y轴交于点C（0，3），点P在该抛物线的对称轴上，且纵坐标为2．（1）求抛物线的表达式以及点P的坐标；（2）当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”．①当D在射线AP上，如果∠DAB为△ABD的特征角，求点D的坐标；②点E为第一象限内抛物线上一点，点F在x轴上，CE⊥EF，如果∠CEF为△ECF的特征角，求点E的坐标．29．（2020•虹口区一模）在平面直角坐标系中，将抛物线C1：y＝x2﹣2x向左平移2个单位，向下平移3个单位得到新抛物线C2．（1）求新抛物线C2的表达式；（2）如图，将△OAB沿x轴向左平移得到△O′A′B′，点A（0，5）的对应点A′落在平移后的新抛物线C2上，求点B与其对应点B′的距离．30．（2020•青浦区一模）如图，在平面直角坐标系xOy中，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于点C，对称轴为直线x＝2，点A的坐标为（1，0）．（1）求该抛物线的表达式及顶点坐标；（2）点P为抛物线上一点（不与点A重合），连接PC．当∠PCB＝∠ACB时，求点P 的坐标；（3）在（2）的条件下，将抛物线沿平行于y轴的方向向下平移，平移后的抛物线的顶点为点D，点P的对应点为点Q，当OD⊥DQ时，求抛物线平移的距离．参考答案一．选择题1．解：（A）由图象的开口方向可知：a＜0，故A正确；（B）由对称轴可知：x＝＜0，∴b＜0，故B错误；（C）由图象可知：c＞0，故C正确；（D）∵a＜0，b＜0，c＞0，∴abc＞0，故D正确；故选：B．2．解：由图象开口可知：a＜0，由图象与y轴交点可知：c＜0，由对称轴可知：＜0，∴a＜0，b＜0，c＜0，故选：D．3．解：在二次函数y＝﹣（x+3）2中，a＝﹣1＜0，∴这个二次函数的图象有最高点（﹣3，0），故选：B．4．解：由“上加下减，左加右减”的原则可知，将二次函数y＝2（x﹣2）2的图象向左平移1个单位，再向下平移3个单位后，得以新的抛物线的表达式是，y＝2（x﹣2+1）2﹣3，即y＝2（x﹣1）2﹣3，故选：C．5．解：∵抛物线y＝x2+4x+1＝（x+2）2﹣3的顶点坐标为（﹣2，﹣3），抛物线y＝x2+1的顶点坐标为（0，1），∴顶点由（﹣2，﹣3）到（0，1）需要向右平移2个单位再向上平移4个单位．故选：C．6．解：A、y＝2x+1，是一次函数，故此选项错误；B、y＝（x﹣1）2﹣x2，是一次函数，故此选项错误；C、y＝1﹣x2，是二次函数，符合题意；D、y＝，是反比例函数，不合题意．故选：C．7．解：A、y＝x属于一次函数，故本选项错误；B、y＝的右边不是整式，不是二次函数，故本选项错误；C、y＝x﹣2+x2＝x2+x﹣2，符合二次函数的定义，故本选项正确；D、y＝的右边不是整式，不是二次函数，故本选项错误；故选：C．8．解：∵y＝2（x+2）2﹣3∴抛物线的顶点坐标是（﹣2，﹣3）故选：B．9．解：把抛物线y＝﹣2x2向上平移1个单位，则得到的抛物线的表达式是：y＝﹣2x2+1．故选：C．10．解：①将（1，0）代入可得：2k﹣（4k+1）﹣k+1＝0，解得：k＝0，此选项正确．②当k＝0时，y＝﹣x+1，该函数的函数值y始终随x的增大而减小；此选项正确；③当k＝0时，y＝﹣x+1，经过3个象限，当k≠0时，△＝（4k+1）2﹣4×2k（﹣k+1）＝24k2+1＞0，∴抛物线必与x轴相交，∴图象必经过三个象限，此选项错误；④当k＝0时，函数无最大、最小值；k≠0时，y＝﹣，当k＞0时，有最小值，最小值为负；当k＜0时，有最大值，最最大值为正；此选项正确．正确的是①②④．故选：C．11．解：∵抛物线y＝x2向左平移1个单位后，所得新抛物线的表达式为y＝（x+1）2，故选：C．12．解：∵将抛物线y＝﹣2x2向上平移1个单位，∴平移后的抛物线的解析式为：y＝﹣2x2+1．故选：D．13．解：抛物线y＝（x﹣1）2的顶点坐标为（1，0），∵向左平移2个单位，∴平移后的抛物线的顶点坐标为（﹣1，0），∴所得抛物线的表达式为y＝（x+1）2．故选：A．14．解：y＝﹣（x+1）2+4＝﹣x2﹣2x+3向下平移3个单位，使它经过原点y＝﹣x2﹣2x，故选：A．15．解：∵抛物线开口向下，对称轴大于1，与y轴交于正半轴，∴a＜0，﹣＞1，c＞0，∴b＞﹣2a，∴b+2a＞0．故选：D．二．填空题（共9小题）16．解：根据题意，得y＝200（1+x）2＝200x2+400x+200．故答案为y＝200x2+400x+200．17．解：因为A（2，5），B（﹣3，5）的纵坐标相同，∴A、B关于x＝＝﹣对称，∴抛物线的对称轴x＝﹣，故答案为x＝﹣．18．解：y＝a2x2+8a2x+a＝a2（x2+8x）+a＝a2（x+4）2+a﹣16a2，∴对称轴x＝﹣4，∵x分别取﹣6、﹣4时，在对称轴左侧，∴y随x的增大而减小，∴y1＞y2，故答案为＞．19．解：∵抛物线y＝﹣3x2向下平移4个单位，∴抛物线的解析式为y＝﹣3x2﹣4，故答案为：y＝﹣3x2﹣4．20．解：∵﹣2＜0，∴二次函数的开口向下，则图象在对称轴左侧的部分y随x值的增大而增大，故答案为上升．21．解：∵抛物线y＝ax2﹣1的顶点是它的最低点，∴抛物线的开口向上，∴a＞0，故答案为a＞0．22．解：抛物线y＝2x2﹣1的对称轴x＝0，抛物线开口向上，∴在对称轴左侧y随x的增加而减小，故答案为下降．23．解：抛物线y＝2（x+1）2向上平移1个单位后的解析式为：y＝2（x+1）2+1．再向右平移1个单位所得抛物线的解析式为：y＝2x2+1．故答案为：y＝2x2+1．24．解：∵y＝x2+4x+5＝（x+2）2+1，∴抛物线y＝x2+4x+5向右平移2个单位后，所得抛物线的表达式为y＝x2+1．故答案为：y＝x2+1．三．解答题（共6小题）25．解：（1）∵抛物线y＝﹣x2+bx+c经过点A（3，0）和B（0，3），∴，解得，∴抛物线的解析式为y＝﹣x2+2x+3，∴顶点C（1，4）．（2）设M（m，﹣m2+2m+3），∴M的反射点为（﹣m2+2m+3，m），∵M点的反射点在抛物线的对称轴上，∴﹣m2+2m+3＝1，∴m2﹣2m﹣2＝0，解得m＝1±，∴M（1+，1）或（1﹣，1）．（3）如图，设P（a，﹣a2+2a+3）．∵A（3，0），B（0，3），C（1，4），∴BC＝，AB＝3，AC＝2，∴AB2+BC2＝AC2，∴∠ABC＝90°，∴tan∠ACB＝＝＝3，∵∠POA＝∠ACB，∴tan∠POA＝3，∴＝3，整理得：a2+a﹣3＝0解得a＝或（舍弃），∴P（，）．26．解：（1）将点A的坐标代入抛物线表达式得：0＝a+2a+3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3；抛物线的对称轴为：x＝1，点D的坐标为：（1，4），令y＝0，y＝﹣x2+2x+3＝0，解得：x＝3或﹣1，令x＝0，则y＝3，故点B的坐标为：（3，0）、点C（0，3）；故抛物线的表达式为：y＝﹣x2+2x+3，B的坐标为（3，0）、点D的坐标为（1，4）；（2）设抛物线向右平移了m个单位，则B'、D'的坐标分别为：（m+3，0）、（m+1，4），平移后抛物线的表达式为：y＝﹣（x﹣m﹣1）2+4，∵新抛物线经过原点O，∴当x＝0时，y＝﹣（0﹣m﹣1）2+4＝0，解得：m＝1或﹣3（舍去﹣3），故点B'、D'的坐标分别为：（4，0）、（2，4），如下图，过点D′作D′H∥y轴交B′C于点H，设直线B′C的表达式为：y＝kx+b，则，解得：，故直线B′C的表达式为：y＝﹣x+3，当x＝2时，y＝，故D′H＝4﹣＝；+S△D′HB′＝×D′H×OB′＝××4＝5．△CB'D'的面积＝S△D′HC27．解：（1）设抛物线的解析式为y＝ax2+bx+c（a≠0）．由题意可得：解得：∴抛物线的解析式为：y＝x2+x+1，∵y＝x2+x+1＝（x+）2+，∴顶点D的坐标（﹣，）；（2）如图，过点B作BF⊥x轴于F，延长CA交BF于点D，过点A作AM⊥BC于M，∴BF＝3，∵A（0，1），C（﹣1，1），∴AC∥x轴，∴CD⊥BF，∴CD＝BD＝2，AD＝1，CA＝1，∴BC＝2，∠BCD＝∠CBD＝45°，∵AM⊥BC，∴∠MAC＝∠MCA＝45°，∴CM＝AM，∴CM＝AM＝＝，∴BM＝BC﹣CM＝，∴tan∠ABC＝＝；（3）∵A（0，1），B（1，3），C（﹣1，1），∴直线AC解析式为：y＝1，直线AB解析式为：y＝2x+1，直线BC解析式为：y＝x+2，若BE∥AC，则点E的纵坐标为3，且点E在对称轴上，∴点E（﹣，3）；若CE∥AB，则CE的解析式为；y＝2x+3，∵点E在对称轴上，∴x＝﹣，∴y＝2，即点E（﹣，2）；若AE∥BC，则AE解析式为：y＝x+1，∵点E在对称轴上，∴x＝﹣，∴y＝，即点E（﹣，），综上所述：点E的坐标为（﹣，3）或（﹣，2）或（﹣，）．28．解：（1）抛物线y＝﹣x2+bx+c与y轴交于点C（0，3），则c＝3，将点A的坐标代入抛物线表达式并解得：b＝2，故抛物线的表达式为：y＝﹣x2+2x+3；点P（1，2）；（2）由点A、P的坐标知，∠PAB＝60°，直线AP的表达式为：y＝（x+1）…①，当α＝60°，∠DBA＝＝30°时，△ABD为直角三角形，由面积公式得：y D×AB＝AD•BD，即y D×4＝2×，解得：y D＝，点D在AP上，故点D（0，）；当∠ADB＝β时，则∠ABD＝90°，故点D（3，4）；综上，点D的坐标为：（0，）或（3，4）；（3）∠CEF为△ECF的特征角，则△CEF为等腰直角三角形，过点E分别作x轴、y轴的垂线交于点M、N，则△CNE≌△EMF（AAS），则EN＝EM，即x＝y，x＝y＝﹣x2+2x+3，解得：x＝，故点E（，）．29．解：（1）由抛物线C1：y＝x2﹣2x＝（x﹣1）2﹣1知，将其向左平移2个单位，向下平移3个单位得到新抛物线C2的表达式是：y＝（x﹣1+2）2﹣1﹣3，即y＝（x+1）2﹣4；（2）由平移的性质知，点A与点A′的纵坐标相等，所以将y＝5代入抛物线C2，得（x+1）2﹣4＝5，则x＝﹣4或x＝2（舍去）所以AA′＝4，根据平移的性质知：BB′＝AA′＝4，即点B与其对应点B′的距离为4个单位．30．解：（1）∵对称轴为直线x＝2，点A的坐标为（1，0），∴点B的坐标是（3，0）．将A（1，0），B（3，0）分别代入y＝x2+bx+c，得．解得．则该抛物线解析式是：y＝x2﹣4x+3．由y＝x2﹣4x+3＝（x﹣2）2﹣1知，该抛物线顶点坐标是（2，﹣1）；（2）如图1，过点P作PN⊥x轴于N，过点C作CM⊥PN，交NP的延长线于点M，∵∠CON＝90°，∴四边形CONM是矩形．∴∠CMN＝90°，CO＝MN、∴y＝x2﹣4x+3，∴C（0，3）．∵B（3，0），∴OB＝OC＝3．∵∠COB＝90°，∴∠OCB＝∠BCM＝45°．又∵∠ACB＝∠PCB，∴∠OCB﹣∠ACB＝∠BCM﹣∠PCB，即∠OCA＝∠PCM．∴tan∠OCA＝tan∠PCM．∴＝．故设PM＝a，MC＝3a，PN＝3﹣a．∴P（3a，3﹣a），将其代入抛物线解析式y＝x2﹣4x+3，得（3a）2﹣4（3﹣a）+3＝3﹣a．解得a1＝，a2＝0（舍去）．∴P（，）．（3）设抛物线平移的距离为m，得y＝（x﹣2）2﹣1﹣m．∴D（2，﹣1﹣m）．如图2，过点D作直线EF∥x轴，交y轴于点E，交PQ延长线于点F，∵∠OED＝∠QFD＝∠ODQ＝90°，∴∠EOD+∠ODE＝90°，∠ODE+∠QDP＝90°．∴∠EOD＝∠QDF．∴tan∠EOD＝tan∠QDF，∴＝．∴＝．解得m＝．故抛物线平移的距离为．。