浙教版七年级数学下册平行线讲义
- 格式:docx
- 大小:180.29 KB
- 文档页数:7


一. 平行线的有关概念及性质公理1.平行线定义在同一平面内,不相交的两条直线叫做平行线,平行线用符号“∥”表示。
如果直线AB与直线CD是平行线,记作“AB∥CD”,读作“AB平行于CD”。
温馨提示(1)平行线必在同一个平面。
(2)平行线指的是“两条直线”,而不是两条射线或线段。
今后遇到题目中说线段或射线平行时,那就特指线段或射线所在的直线平行。
2.平行线公理经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
即:如果a∥b,c ∥b,那么a∥c。
3.平行线的性质(1)两条平行线被第三条直线所截,同位角相等。
即:两直线平行,同位角相等。
(2)两条平行线被第三条直线所截,内错角相等。
即:两直线平行,内错角相等。
(3)两条平行线被第三条直线所截,同旁内角互补。
即:两直线平行,同旁内角互补。
4.平行线的判定(1)两条平行线被第三条直线所截,如果同位角相等,那么这两条直线平行。
即:同位角相等,两直线平行。
(2)两条平行线被第三条直线所截,如果内错角相等,那么这两条直线平行。
即:内错角相等,两直线平行。
(3)两条平行线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
即:同旁内角互补,两直线平行。
温馨提示(1)还可以根据平行线的传递性(如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
即:如果a∥b,c∥b,那么a∥c)来判断两直线平行。
(2)垂直于同一条直线的两条直线平行。
二.课堂练习1.如图,直线a,b被直线c所截,下列说法正确的是()。
A.当∠1∥∠2时,一定有a∥bB.当a∥b时,一定有∠1∥∠2C.当a∥b时,一定有∠1+∠2=90°D.当∠1+∠2=180°时,一定有a∥b2.如右图所示,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是()。
A.40°B.50°C.60°D.70°3.如图所示,已知∠ADE=∠B,FG⊥AB,∠EDC=∠GFB,求证:CD⊥AB。

【第一章《平行线》复习】1.1、同位角、内错角、同旁内角:1、先看图中∠1和∠5,这两个角分别在直线AB、CD的上方,并且都在直线EF的右侧像这样位置相同的一对角叫做同位角。
在图(1)中,像这样具有类似位置关系的角还有吗?如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角。
变式图形:图中的∠1与∠2都是同位角。
图形特征:在形如字母“F”的图形中有同位角。
2、再看∠3与∠5,这两个角都在直线AB、CD之间,且3在直线EF左侧,∠5在直线EF右侧,像这样的一对角叫做内错角。
同样,∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。
变式图形:图中的∠1与∠2都是内错角。
图形特征:在形如“Z”的图形中有内错角。
3、在图(1)中,∠3和∠6也在直线AB、CD之间,但它们在直线EF的同一旁像这样的一对角,我们称它为同旁内角。
具有类似的位置特征的还有∠4与∠5,因此它们也是同旁内角。
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“n”的图形中有同旁内角。
与两直线的位置关系与截线的位置关系同位角两直线同侧截线的同旁内错角两直线之间截线异侧同旁内角两直线之间截线同侧1.2、平行线的性质:性质1:两条直线被第三条直线所截,如果两条直线平行,那么同位角相等。
简单说成:两直线平行,同位角相等。
几何语言:∵ AB//CD ∴ ∠PMA=∠MNC性质2:两条直线被第三条直线所截,如果两条直线平行,那么内错角相等。
简单说成:两直线平行,内错角相等。
几何语言:∵ AB//CD ∴ ∠BMN=∠CNM性质3:两条直线被第三条直线所截,如果两条直线平行,那么同旁内角互补。
简单说成:两直线平行,同旁内角互补。
几何语言:∵ AB//CD ∴ ∠AMN+∠CNM=180°1.3、平行线的判定: 几何符号语言:(1)∵ ∠3=∠2 ∴ AB ∥CD (同位角相等,两直线平行) (2)∵ ∠1=∠2 ∴ AB ∥CD (内错角相等,两直线平行)(3)∵ ∠4+∠2=180° ∴ AB ∥CD (同旁内角互补,两直线平行)1.4、两条平行线的距离如图,直线AB ∥CD ,EF ⊥AB 于E ,EF ⊥CD 于F ,则称线段EF 的长度为两平行线AB 与CD 间的距离。

浙教版七年级数学下册精品课件 11 平行线一、教学内容本节课选自浙教版七年级数学下册第十一章“平行线”,具体内容包括:平行线的定义、性质、判定方法以及平行线之间的距离。
本章共分为两节,本节课将详细讲解第一节内容。
二、教学目标1. 让学生掌握平行线的定义、性质和判定方法,能熟练运用这些知识解决实际问题。
2. 培养学生运用几何图形进行分析、推理的能力。
3. 培养学生的空间观念,提高学生的数学素养。
三、教学难点与重点重点:平行线的定义、性质和判定方法。
难点:平行线之间的距离的计算。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:直尺、量角器、三角板。
五、教学过程1. 实践情景引入:展示生活中的平行线实例,如铁轨、双杠等,引导学生观察并思考:什么是平行线?2. 教学平行线的定义:引导学生通过观察、思考和讨论,得出平行线的定义:在同一平面内,两条永不相交的直线叫做平行线。
3. 例题讲解:讲解平行线的性质和判定方法,如同位角相等、内错角相等、同旁内角互补等。
4. 随堂练习:让学生运用刚学过的性质和判定方法,分析并解决实际问题。
5. 教学平行线之间的距离:讲解如何计算两条平行线之间的距离,并通过例题进行演示。
六、板书设计1. 平行线的定义2. 平行线的性质同位角相等内错角相等同旁内角互补3. 平行线的判定方法4. 平行线之间的距离计算七、作业设计1. 作业题目:(1)判断下列说法是否正确,并说明理由:a. 在同一平面内,两条直线如果不相交,就是平行线。
b. 在同一平面内,两条直线如果同位角相等,就是平行线。
(2)计算下列平行线之间的距离:c. 平行线3x4y+7=0和3x4y5=0之间的距离。
2. 答案:(1)a. 正确;b. 错误,还需满足其他条件。
(2)c. 距离为3。
八、课后反思及拓展延伸1. 反思:本节课学生对平行线的定义、性质和判定方法掌握较好,但在计算平行线之间的距离时,部分学生存在一定困难。
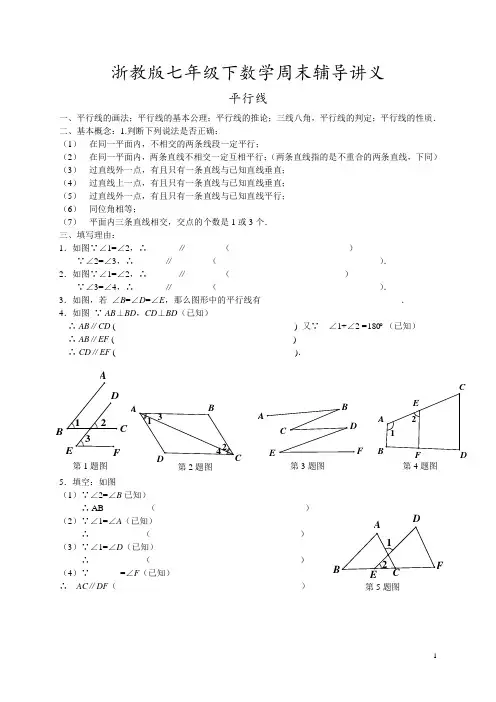
1浙教版七年级下数学周末辅导讲义平行线一、平行线的画法;平行线的基本公理;平行线的推论;三线八角,平行线的判定;平行线的性质. 二、基本概念:1.判断下列说法是否正确:(1) 在同一平面内,不相交的两条线段一定平行; (2) 在同一平面内,两条直线不相交一定互相平行;(两条直线指的是不重合的两条直线,下同) (3) 过直线外一点,有且只有一条直线与已知直线垂直; (4) 过直线上一点,有且只有一条直线与已知直线垂直; (5) 过直线外一点,有且只有一条直线与已知直线平行; (6) 同位角相等;(7) 平面内三条直线相交,交点的个数是1或3个. 三、填写理由:1.如图∵∠1=∠2,∴_______∥________( )∵∠2=∠3,∴_______∥________( ). 2.如图∵∠1=∠2,∴_______∥________( )∵∠3=∠4,∴_______∥________( ). 3.如图,若 ∠B =∠D =∠E ,那么图形中的平行线有________________________________. 4.如图 ∵ AB ⊥BD ,CD ⊥BD (已知)∴ AB ∥CD ( ) 又∵ ∠1+∠2 = 180(已知) ∴ AB ∥EF ( ) ∴ CD ∥EF ( ).5.填空:如图(1)∵∠2=∠B 已知)∴ AB__________() (2)∵∠1=∠A (已知)∴ __________() (3)∵∠1=∠D (已知)∴ __________( ) (4)∵_______=∠F (已知)∴ AC ∥DF ( )B C 第1题图A第2题图 第4题图 A F 第3题图 CE 第5题图26.如图:已知∠A =∠D ,∠B =∠FCB ,判定ED 与CF 的位置关系,并说明理由.7.如图,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME .求证:AB ∥CD ,MP ∥NQ .8.如图,∠ABD 和∠BDC 的平分线交于E ,BE 交CD 于点F ,∠1 +∠2 = 90°.求证:(1)AB ∥CD ; (2)∠2 +∠3 = 90°.9. 已知:如图, AB ∥EF ∥CD ,EG 平分∠BEF ,∠B +∠BED +∠D =192°,∠B -∠D =24°,求∠GEF 的大小.10.已知:如图,AB ∥CD ,求证:∠B +∠D +∠F =∠E +∠G .C DAF第6题图C 第8题图 AF 第9题图F 第10题图3测试题:1.如图1,a ∥b ,a 、b 被c 所截,得到∠1=∠2的依据是( ) A .两直线平行,同位角相等 B .两直线平行,内错角相等 C .同位角相等,两直线平行 D .内错角相等,两直线平行(1) (2) (3)2.同一平面内有四条直线a ,b ,c ,d ,若a ∥b ,a ⊥c ,b ⊥d ,则直线c 、d 的位置关系为( ) A .互相垂直 B .互相平行 C .相交 D .无法确定 3.如图2,如果AB ∥CD ,那么( )A .∠1=∠4B .∠1=∠3C .∠2=∠3D .∠1=∠5 4.如图3,在平行四边形ABCD 中,下列各式不一定正确的是( ) A .∠1+∠2=180° B .∠2+∠3=180°C .∠3+∠4=180°D .∠2+∠4=180° 5.如图4,AD ∥BC ,∠B =30°,DB 平分∠ADE ,则∠DEC 的大小为( )A .30°B .60°C .90°D .120°6.如图5,AB ∥EF ,BC ∥DE ,则∠E +∠B 的度数为________.7.如图,AB ∥CD ,AE 、DF 分别是∠BAD 、∠CDA 的角平分线,AE 与DF 平行吗?为什么? 8.(1)如图6,已知AB ∥CD ,直线l 分别交AB 、CD •于点E 、F ,EG 平分∠BEF ,若∠EFG =40则∠EGF 的大小是( )A .60°B .70°C .80°D .90° (2)如图7,已知AB ∥DE ,∠E =65°,则∠B +∠C 的大小是( ) A .135° B .115° C .65° D .35° 9.(1)如图,若AB ∥DE ,∠B =135°,∠D =145°,你能求出∠C 的度数吗?(2)在AB ∥DE 的条件下,你能得出∠B 、∠C 、∠D 之间的数量关系吗?并说明理由.图7 图6图4 图5 第7题图。

浙教版初一数学下平行线知识点讲解知识点1、平行线的定义:在同一平面内,永不相交的两条直线叫做平行线.如:AB平行于CD,写作AB∥CD2、平行公理:过直线外一点有且只有一条直线与已知直线平行.推论(平行线的传递性):平行同一直线的两直线平行.∵a∥c,c∥bthere4;a∥b.课后练习1. 两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2. 两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为------__________.对顶角的性质:______ _________.3. 两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4. 直线外一点到这条直线的垂线段的长度,叫做________________________.5. 两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.答案:1.邻补角2.对顶角,对顶角相等3.垂直有且只有垂线段最短4.点到直线的距离5.同位角内错角同旁内角平行线知识点的全部内容就是这些,不知道大家是否已经都掌握了呢?预祝大家以更好的学习,取得优异的成绩。

浙教版七年级数学下册课件 11 平行线一、教学内容本节课的教学内容来自于浙教版七年级数学下册,第11章“平行线”。
本章主要内容包括:平行线的定义、性质、判定以及平行线的画法。
在本节课中,我们将重点讲解平行线的判定方法。
二、教学目标1. 让学生理解平行线的定义,掌握平行线的性质和判定方法。
2. 培养学生运用平行线的知识解决实际问题的能力。
3. 提高学生的逻辑思维能力和团队合作能力。
三、教学难点与重点重点:平行线的定义、性质和判定方法。
难点:平行线的判定方法的灵活运用。
四、教具与学具准备教具:黑板、粉笔、直尺、圆规。
学具:练习本、铅笔、橡皮、直尺。
五、教学过程1. 实践情景引入:让学生观察教室里的窗户,引导学生发现窗户的框架是由平行线组成的。
5. 例题讲解:给出一个例题,引导学生运用平行线的判定方法解决问题。
6. 随堂练习:让学生独立完成一些相关的练习题,巩固所学知识。
7. 平行线的画法:引导学生学习平行线的画法,并进行实际操作。
六、板书设计板书设计如下:平行线定义:在同一平面内,永不相交的两条直线叫做平行线。
性质:平行线之间的距离相等;平行线与横截线所成的角相等。
判定方法:同位角相等;内错角相等;同旁内角互补。
画法:使用直尺和圆规,按照一定的步骤进行画法。
七、作业设计1. 请用直尺和圆规画出两条平行线,并标出它们之间的距离。
答案:略答案:略八、课后反思及拓展延伸在课后,学生可以通过画图和解决实际问题,进一步巩固平行线的知识。
学生还可以学习其他几何图形的性质和判定方法,提高自己的数学素养。
重点和难点解析:一、教学内容解析本节课的教学内容主要来自于浙教版七年级数学下册的第11章“平行线”。
在这一章节中,学生将学习平行线的定义、性质、判定方法以及平行线的画法。
这些内容是学生理解和掌握平行线知识的基础,也是本节课的教学重点。
二、教学目标解析本节课的教学目标有三个,分别是让学生理解平行线的定义,掌握平行线的性质和判定方法,以及提高学生的逻辑思维能力和团队合作能力。


基础巩固篇第一讲平行线及其判定思维导图重难点分析重点分析:1. 在同一平面内,不相交的两条直线叫做平行线,用符号“∥”表示.2. “三线八角” :两条直线被第三条直线所截,构成八个角,称为“三线八角” ,这八个角中,同位角有四对,内错角有两对,同旁内角有两对.3. 平行线的判定方法:(1)根据定义判定;(2)三个判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;(3)平行的传递性;(4)在同一平面内,垂直于同一条直线的两条直线互相平行.难点分析:1. 平行线必在同一平面内,分别在两个平面内的两条直线,即使不相交,也不一定平行.2. 过已知直线外一点,有且只有一条直线与已知直线平行,这一性质指出了过直线外一点作这条直线的平行线的“存在性”和“唯一性” ,要注意“直线外一点”这一条件.3. 平行线的判定定理是通过角的关系说明直线的位置关系,实现了几何条件之间的转化,应用定理时要注意正确判断角的位置特征.例题精析例1、在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行,其中正确的个数为().A.1 个B.2 个C.3 个D.4 个思路点拨:根据直线的性质公理、相交线的定义、垂线的性质、平行公理对各小题分析判断后即可得解.解题过程:①过两点有且只有一条直线,正确;②两条不相同的直线若相交则有且只有一个公共点,若平行则没有公共点,故错误;③经过直线外一点有且只有一条直线与已知直线垂直,正确;④经过直线外一点有且只有一条直线与已知直线平行,正确;综上所述,正确的有①③④共 3 个. 故选 C.方法归纳:本题考查了平行公理、直线的性质、垂线的性质以及相交线的定义,属于基础概念题,熟记概念是解题的关键.易错误区:两条不相同的直线除了平行外,如果不在同一平面内,也可能没有公共点.例2、如图,标有角号的7 个角中共有对内错角,对同位角,对同旁内角.思路点拨:根据内错角、同位角及同旁内角的定义判断即可求得本题. 解题过程:共有 4 对内错角:分别是∠ 1和∠4,∠2 和∠5,∠6 和∠1,∠5和∠7;2 对同位角:分别是∠ 7 和∠ 1 ,∠ 5 和∠ 6 ;4对同旁内角:分别是∠ 1和∠5,∠3 和∠ 4,∠ 3和∠ 2,∠ 4和∠ 2. 方法归纳:三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由这两个角在图形中的相对位置决定. 在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.易错误区:同位角的边构成“ F”形,内错角的边构成“ Z”形,同旁内角的边构成“ U”形. 图形较为复杂,要注意从复杂的图形中分解出基本图形.例3、(1)如图1,AB,CD,EF 是三条公路,且AB⊥EF,CD⊥EF.试判断AB与CD的位置关系,并说明理由;(2)如图2,在(1)的条件下,若小路OM平分∠ EOB,通往加油站N的岔道O′N平分∠ CO′ F,试判断OM与O′N 的位置关系.思路点拨:(1)根据在同一平面内,垂直于同一直线的两条直线互相平行,即可证得AB∥ CD;(2)可通过构建直线OM与O′N 的同位角来得出OM∥O′ N的结论.解题过程:(1)∵ AB⊥EF,CD⊥ EF,∴ AB∥ CD(在同一平面内,垂直于同一直线的两条直线互相平行).(2)如图,延长NO′与AB交于点P.∵OM平分∠ EOB,O′ N平分∠ CO′F,∴∠ EOM=∠FO′N=45° .∵∠ FO′ N=∠ EO′ P,∴∠ EOM=∠EO′P=45° .∴ OM∥ O′N(同位角相等,两直线平行).方法归纳:本题主要考查了平行线的判定方法. 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.易错误区:第(2)题中虽然有∠ EOM与∠ FO′N相等,但它们不是同位角,不能直接用来判定两直线平行.例4、如图,∠ ABD和∠ BDC的平分线交E,BE的延长线交CD于点F,∠ 1+∠2=90°.于点(1)求证:AB∥ CD;(2)试探究∠ 2 与∠3 的数量关系.思路点拨:(1)根据BE,DE分别平分∠ ABD,∠BDC,且∠ 1+∠2=90°,可得∠ ABD+∠ BDC=180°,根据同旁内角互补,可得两直线平行;(2)根据∠ 1+∠ 2=90°,可得∠ BED=90°,从而可得∠3+∠FDE=90°,将等角代换,即可得出∠ 3与∠2 的数量关系解题过(1)证明:∵ BE,DE分别平分∠ ABD,∠ BDC,11 ∴∠1= ∠ ABD,∠ 2= ∠BDC.22 ∵∠ 1+∠2=90°,∴∠ ABD+∠ BDC=180° . ∴ AB∥ CD(同旁内角互补,两直线平行). (2)∵ DE平分∠ BDC,∴∠ 2=∠ FDE. ∵∠ 1+∠2=90°,∴∠ BED=∠ DEF=90°. ∴∠ 3+∠ FDE=90°. ∴∠ 2+∠3=90°. 方法归纳:本题主要考查了角平分线的性质以及平行线的判定,注意题中各角之间的数量关系要理清楚.易错误区:第(2)题中的数量关系不是等量关系,不要误认为∠2=∠3.例5、如图1,已知∠ EAC=90°,∠ 1+∠2=90°,∠ 1=∠ 3,∠ 2=∠4. 求证:(1)DE∥BC;2)若将图形改变为图2、图3,其他条件不变,1)中的结论是否成立?若成立,请选择一个图形予以证明;若不成立,思路点拨:(1)首先证明∠ 1+∠3+∠ 2+∠4=180°,进而证明∠ D+∠B=180°,即可解决问题;(2)在图 2 中,连结CE,证明∠ AEC+∠ACE+∠3+∠ 4=180°,即可解决问题. 解题过程:(1)如图1,∵∠ 1=∠ 3,∠ 2=∠4,∴∠ 1+∠ 3+∠ 2+∠ 4=2(∠ 1+∠2).∵∠ 1+∠ 2=90°,∴∠ 1+∠ 3+∠ 2+∠4=180°.∵∠ D+∠ B+∠ 1+∠3+∠2+∠4=360°,∴∠ D+∠ B=180° .∴DE∥BC(同旁内角互补,两直线平行)(2)成立. 如图,连结EC.∵∠ 1=∠ 3,∠ 2=∠4,且∠ 1+∠2=90°,∴∠ 3+∠ 4=∠ 1+∠2=90°.∵∠ EAC=90°,∴∠ AEC+∠ACE=180° -90 °=90°.∴∠ AEC+∠ACE+∠3+∠ 4=180°. ∴DE∥BC(同旁内角互补,两直线平行)∴(1)中的结论仍成立.图 3 用类似方法可得DE∥ BC.方法归纳:本题考查了平行线的判定问题,解题的关键是灵活运用三角形的内角度数关系(三角形三个内角和等于180°),结合平行线的判定定理来分析、判断、解答易错误图 2 通过连结EC将∠3 和∠ 4的关系用三角形联系起来是本题探究提升例、三条直线两两相交于三点(如图1),共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?四条直线两两相交呢(如图2)?你能发现n 条直线两两相交的规律吗?思路点拨: 解题的关键在于找到每个图形中含有几个三线八角的基本图形, 三条直线两两相交, 共有 3 个三线八角的基本图形;四条直线两两相交有 12 个三线八角的基本图形 .n 条直线中任选两条有 n (n 1) 种选法,然后在剩下的( n-2)条直线中任选一条直线作为截线共有( n-2 )2 种选法,所以 n 条直线两两相交共有 n (n 1)(n 2) 个三线八角的基本图形 .2解题过程: 三条直线两两相交于三点,共有 6 对对顶角, 12 对邻补角, 12 对同位角, 6 对内 错角, 6对同旁内角;四条直线两两相交,共有 12 对对顶角, 24对邻补角, 48 对同位角, 24 对内错角, 24 对同旁内角; n 条直线两两相交,共有 nn-1 对对顶角, 2nn-1 对邻补角, 2nn-1 ( n-2 )对同位角, nn-1 (n-2 )对内错角, nn-1 ( n-2 )对同旁内角 .方法归纳: 对于规律题关键在于找出规律,但在找到规律的同时还需要明确基本图形的特征 . 易错误区: 本题通过分解图形,利用“三线八角”这一基本图形解决问题,仅利用图形找角是 不容易找全的 .专项训练拓展训练A 组3. 如图,请填写一个你认为恰当的条件: ,使 AB ∥ CD.4. 如图,有下列判断:①∠ A 与∠ 1是同位角;②∠ A 与∠ B 是同旁内角;③∠ 4 与∠ 1是内错 角;④∠ 1与∠3是同位角 .其中正确的是 (填序号) .1. 如图,列条件中,能判定 DE ∥ AC 的是( 1 题)②④ ).A. ①②2. 如图,(第 8 题)5. 如图,∠ A=70°, O 是 AB 上一点,直线 CO与 AB 所夹的∠ BOC=82°,当直线 OC 绕点 O 按逆 时针方向至少旋转 °时, OC ∥ AD. 6. 如图,已知∠ 1=∠2,∠ BAC=20°,∠ ACF=80°. ( 1)求∠ 2 的度数; (2)FC 与 AD 平行吗?为什么? (3)根据以上结论,你能确定∠B 组7.在同一平面内,有 l 1,l 2,l 3,l 4四条直线,若 l 1⊥l 2,l 2⊥l 3, l 3⊥l 4, A.l B.lC.lD.l8.如图, AB ⊥ BC ,∠ 1+∠ 2=90°,∠ 2=∠3.求证: BE ∥DF.则( ) .1⊥l 3, 1∥l 3, 1∥l 3, 1∥l 4, l 2 ⊥l 4 l 2 ⊥l 4 l 1 ⊥l 4 l 2 ⊥l 4 9. 如图, BD ⊥ AC 于点 D , EF ⊥ AC 于点 F ,∠ AMD=∠ AGF ,∠1=∠ 2=35° . ( 1)求∠ GFC 的度数;(2)求证: DM ∥ BC.ABCD ,使其拐(第 7题) 走进重高1. 【柳州】如图,与∠ 1 是同旁内角的是( ) .角∠ ABC=150°,∠ BCD=30°,则().A.AB∥BCB.BC∥CDC.AB∥DCD.AB 与CD相交3. 【淄博】如图,一个由4条线段构成的“鱼”形图案,找出图中的平行线,并说明理由.4.如图,已知点E,F在直线AB上,点G在线段CD上,∠GHD.1)求证:CE∥ GF;2)试判断∠ AED与∠ D之间的数量关系,并说明理由;(第 6题)高分夺冠1. 直线a,b,c 在同一平面内,①如果a⊥ b,b⊥c,那么a∥c;②如果a∥ b,b∥c,那么 a ∥ c;③如果a∥b,b⊥c,那么a⊥ c;④如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的有个.4.将一副三角尺中的两个直角顶点C叠放在一起(如图),其中∠ A=30°,∠ B=60°,∠ D=∠E=45°.1)若∠ BCD=150°,求∠ ACE的度数;2)试猜想∠ BCD与∠ ACE之间的数量关系,并说明理由;(3)若按住三角尺ABC不动,绕顶点 C 转动三角尺DCE,试探究∠ BCD等于多少度时,CD∥ AB,并简要说明理由.(第4题)。