七桥问题——一笔画
- 格式:doc
- 大小:628.50 KB
- 文档页数:1

七桥问题与一笔画的通解(论文拟稿)在柯尼斯堡的一个公园里,有七座桥将一条河上的两座岛和两岸相连接。
当时有人提出了这么一个问题:如何一次性不重复不遗漏走完七座桥。
后来,数学家欧拉将它变成了一个一笔画问题(如图)。
从欧拉的简化图来看,似乎我们无论如何,也不能一笔画完图形。
但是,这是为什么呢?在这个图中,有ABCD 4个点,有五条线汇聚到A点,三条线汇聚到B,C,D 点,我们可以把这种有奇数条线(3条及以上)汇聚的点称为奇点,作为对应,把有偶数条线(4条及以上)汇聚的点称为偶点。
那么,我们不难发现,在任意封闭图形中,奇点的个数一定是偶数。
因为一条线定连接两个点(或重合),若存在奇数个奇点,则此图形定不符合封闭图形定义。
从一个奇点来看,若要一笔画成,则此奇点定是起笔点或停笔点。
起笔点,停笔点只有两个,所以说,奇点为两个或没有奇点的封闭图形可以一笔画。
回来看七桥问题,图中有四个奇点,以任意两个作为起笔点和落笔点,则还有两个奇点无法连接。
故七桥问题无解。
从上面总结出以下结论:■⒈凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
■⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点为终点。
■⒊其他情况的图都不能一笔画出。
(奇点数除以二便可算出此图需几笔画成。
)我们可以把得到的结论推广到所有一笔画解法存在问题,如汉字“田”,我们观察到,它有四个奇点,故不可以一笔画。
而汉字“日”,只有两个奇点,则可以一笔画。
早在1736年,欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》的论文报告中,就阐述了这种方法,也为后来的数学新分支--拓扑学的建立奠定了基础。
从这里我们可以看出,伟大的创造一开始可能并不像我们想象的那么高深莫测,仔细观察生活,我们也会有了不起的发现。



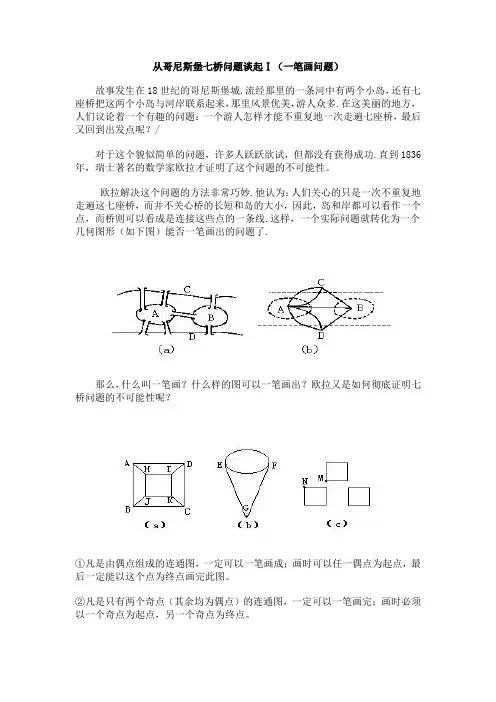
从哥尼斯堡七桥问题谈起Ⅰ(一笔画问题)故事发生在18世纪的哥尼斯堡城.流经那里的一条河中有两个小岛,还有七座桥把这两个小岛与河岸联系起来,那里风景优美,游人众多.在这美丽的地方,人们议论着一个有趣的问题:一个游人怎样才能不重复地一次走遍七座桥,最后又回到出发点呢?/对于这个貌似简单的问题,许多人跃跃欲试,但都没有获得成功.直到1836年,瑞士著名的数学家欧拉才证明了这个问题的不可能性。
欧拉解决这个问题的方法非常巧妙.他认为:人们关心的只是一次不重复地走遍这七座桥,而并不关心桥的长短和岛的大小,因此,岛和岸都可以看作一个点,而桥则可以看成是连接这些点的一条线.这样,一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了.那么,什么叫一笔画?什么样的图可以一笔画出?欧拉又是如何彻底证明七桥问题的不可能性呢?①凡是由偶点组成的连通图,一定可以一笔画成;画时可以任一偶点为起点,最后一定能以这个点为终点画完此图。
②凡是只有两个奇点(其余均为偶点)的连通图,一定可以一笔画完;画时必须以一个奇点为起点,另一个奇点为终点。
③其他情况的图,都不能一笔画出。
下面我们就来研究一笔画问题的具体应用:例1观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.分析与解答例2下图是国际奥委会的会标,你能一笔把它画出来吗?分析与解答例3下图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析与解答例4 下图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析与解答例5一张纸上画有如下图所示的图,你能否用剪刀一次连续剪下图中的三个正方形和两个三角形?分析与解答例6下图是一个公园的平面图.要使游客走遍每条路而不重复,问出入口应设在哪里?分析与解答练习题1.请一笔画出下列各图2.判断下列各图能否一笔画出,并说明理由.3.下图是一公园的平面图,要使游客走遍每一条路且不重复,问出入口应设在哪里?4.下图是一个商场的平面图,顾客可以从六个门进出商场(阴影部分为各商品部,空白处为通道),请你设计一种能够一次走遍各通道而又不必走重复路线的进出方法.。


一笔画问题
1.瑞士大数学家欧拉在七桥问题的过程中,发现了一笔画原理,这一原理被命名为“欧拉定理”:
(1)能一笔画的图形必须是连通的。
(2)凡是只由偶顶点组成的连通图形,一定可以一笔画出,画时可以由任一偶顶点为起点,最后仍回到这点。
(3)凡是只有两个奇顶点的连通图形一定可以一笔画出,画时必须以一个奇顶点为起点,以另一个奇顶点为终点。
(4)奇顶点个数超过两个的图形不能一笔画出。
2.能一笔画出的图形的奇顶点数目是2或0,如果图形有奇顶点2N(n为正整数)个,那么图形最少要用N笔画出。

世界数学难题——哥尼斯堡七桥问题请你做下面的游戏:一笔画出如图1的图形来。
规则:笔不离开纸面,每根线都只能画一次。
这就是古老的民间游戏——一笔画。
你能画出来吗?如果你画出来了,那么请你再看图2能不能一笔画出来?虽然你动了脑筋,但我相信你肯定不能一笔画出来!为什么我的语气这么肯定?我们来分析一下图2。
我们把图2看成是由点和线组成的一种集合。
图里直线的交点叫做顶点,连结顶点的线叫做边。
这个图是联通的,即任何二个顶点之间都有边。
很显然,图中的顶点有两类:一类是有偶数条边联它的,另一类是有奇数条边联它的。
一个顶点如果有偶数条边联它的,这点就称为偶点;如果有奇数条边联它的,就称它为奇点。
我们知道,能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
图2有六个奇点,四个偶点,当然不能一笔画出来了。
为什么能一笔画的图形只有上述两类呢?有关这个问题的讨论,要追溯到二百年前的一个著名问题:哥尼斯堡七桥问题。
十八世纪东普鲁士哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河,它有两个支流,在城市中心汇成大河,中间是岛区,河上有7座桥,将河中的两个岛和河岸连结,如图3所示。
由于岛上有古老的哥尼斯堡大学,有教堂,还有哲学家康德的墓地和塑像,因此城中的居民,尤其是大学生们经常沿河过桥散步。
渐渐地,爱动脑筋的人们提出了一个问题:一个散步者能否一次走遍7座桥,而且每座桥只许通过一次,最后仍回到起始地点。
这就是七桥问题,一个著名的图论问题。
图3这个问题看起来似乎很简单,然而许多人作过尝试始终没有能找到答案。
因此,一群大学生就写信给当时年仅20岁的大数学家欧拉。
欧拉从千百人次的失败,以深邃的洞察力猜想,也许根本不可能不重复地一次走遍这七座桥,并很快证明了这样的猜想是正确的。
欧拉是这样解决问题的:既然陆地是桥梁的连接地点,不妨把图中被河隔开的陆地看成4个点,7座桥表示成7条连接这4个点的线,如图4所示。
图4 图5于是“七桥问题”就等价于图5中所画图形的一笔画问题了。



七桥问题——一笔画
18世纪东普鲁士的哥尼斯堡城,有一条河穿过,河上下有两个小岛,有七座桥把两个岛与河岸联系起来(如下图一)。
有人提出一个问题:一个步行者怎样才能不重复,不遗漏地一次走完七座桥,最后回到出发点。
这个问题提出后在很长一段时间内很多人进行了研究都没有研究出答案。
后来大数学家欧拉把它转化成一个几何问题——一笔画问题,使问题得到了解决。
(如下图二)
图一图二
问题的答案如何呢?让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。
②有偶数条边相连的点叫偶点。
③一笔画指:1、下笔后笔尖不能离开纸。
2、每条线都只能画一次而不能重复。
结论:
课堂练习
1、一辆洒水车要给
再回到出发点?
2、甲乙两个邮递员去送信,两人同时出发以同样的速度走遍所有的街道,甲从A点出发,乙从B点出发,最后都回到邮局(C点)。
如果要选择最短的线路,谁先回到邮局?。
一笔画问题——七桥问题的解决救学内容:“一笔画问题-七桥问题的解决”教学目标:1.让学生体会用“数学模型方法”解决问题。
2.通过其中抽象出点、线的过程,使学生对点、线有进一步的认识。
3.通过探究"一笔画"的规律的活动,锻炼学生克服困难的意志及勇于发表见解的好习惯。
教学重点:数学模型方法的渗透,以及在活动中去寻找规律,发现问题,解决问题。
教学难点:让学生自己探究得出"一笔画"的规律。
教学准备:课件,学习活动单3张,红色水彩笔。
教学过程:导语:同学们,平时生活中,我们要用智瑟的双眼认真观察周边的事物。
今天,老师要和大家上一节有趣的数学活动探究课。
准备好了吗?好,上课!一、故事激趣导入新课:1.小视频(简笔画导入)师:请大家认真观察,(老师边画边说)师:老师画这些图案时都是怎样画成的?2.介绍数学史,建立数学模型:18世纪时风景秀丽的小城哥尼斯堡中有一条河河的中间有两个小岛,河的两岸与两岛之间共建有七座桥(如图),当时小城的居民中流传着一道难题:一个人怎样才能不重复地走过所有七座桥,再回到出发点?这就是数学史上着名的七桥问题,你愿意试一试吗?好,动笔吧。
结果怎样?3.介绍瑞士数学家欧拉。
欧拉把一个实际的生活情景问题转化成合适的“数学模型”。
这种研究方法就是“数学模型方法”。
你们对一笔画问题感兴趣吗?想了解吗?今天我们就来一起研究“一笔画问题”。
(板书)4.什么叫一笔画?什么样的图可以一笔画成?(下笔后笔尖不能离开纸B、每条线都只能画一次而不能重复。
)5.认识连通图。
6.要研究一笔画图案有什么规律,我们必须先来了解两个重要概念:奇点和偶点点:有奇数条边相连的点叫奇点。
(2)偶点:有偶数条边相连的点叫偶点。
二、小组合作实验探究1、师:我们来动手画几幅简单美丽的图案,请大家亲自感受一下!2、小组合作探究委求:D小组合作分工完成8个图形的判断。
(2)完成后一起交流讨论,哪些图形能一笔画完成。
Konigsberg 七橋問題(一筆畫問題)當Euler在1736年訪問Konigsberg,Prussia(now Kaliningrad Russia)時,他發現當地的市民正從事一項非常有趣的消遣活動。
Konigsberg城中有一條名叫Pregel這項有趣的消遣活動是在星期六作一次走過所有七座橋的散步,每座橋只能經過一次,而且起點與終點必須是同一地點。
Euler把每一塊陸地考慮成一個點,連接兩塊陸地的橋以線表示,便得如下的圖形Euler後來推論出此種走法是不可能的。
他的論點是這樣的,除了起點以外,每一次當一個人由一座橋進入一塊陸地(或點)時,他(或她)同時也由另一座橋離開此點。
所以每行經一點時,計算兩座橋(或線),從起點離開的線與最後回到始點的線亦計算兩座橋,因此每一個陸地與其他陸地連接的橋數必為偶數。
我們從Konigsberg七橋所成之圖形中,沒有一點含有偶數條數,因此上述的任務是不可能實現的。
Eulerian graphs 歐拉圖形一條途徑v0e1e2v2………..e k v k稱為Euler walk(歐拉走路)如果沒有邊(edge)是重複的,此處v i表頂點,e i表邊。
若一個圖形G中,v0e1v1e2v2……………e k v k行經每一邊恰好一次,且v0=v k(起點=終點),則稱此途徑為Euler tour(歐拉路徑)。
例:從下右圖中找出一歐拉路徑一.筆劃問題問題:有一商人欲推銷某一商品,該商人在下圖中每一地點,A,B,...,J都希望去推銷該商品,但為了達到最低成本故希望不要重複行走已走過的路徑以減低車費成本,問該商人應如何行走?Eulerian graphs 歐拉圖形一條路徑V0e1V1e2V2…..e k V k稱為Euler walk (歐拉走路)如果沒有邊(edge)是重複的,此處V1表頂點,e1表邊。
若一個圖形G中,V0e1V1e2V2…..e k V k行徑每一邊恰好一次且( 起點=終點),則稱此途徑為Euler tour (歐拉路徑)。