非参数统计部分课后习题参考答案
- 格式:doc
- 大小:161.00 KB
- 文档页数:7

刺膻中穴前后痛阈值的差异有无统计学意义?10名受试者针刺膻中穴前后痛阈资料编号针刺前针刺后1 600 6102 600 7003 685 5754 1050 6005 900 6006 1125 14257 1400 13508 750 8259 1000 80010 1500 14002.雌鼠两组分别给以高蛋白和低蛋白的饲料,实验时间自生后28天至84天止,计8周。
观察各鼠所增体重,结果如下表,问两种饲料对雌鼠体重增加有无显著影响?两种饲料雌鼠体重增加量(g)高蛋白组低蛋白组83 6597 70104 70107 78113 85119 94123 101124 107129 122134146161刺膻中穴前后痛阈值的差异有无统计学意义?10名受试者针刺膻中穴前后痛阈资料编号针刺前针刺后1 600 6102 600 7003 685 5754 1050 6005 900 6006 1125 14257 1400 13508 750 8259 1000 80010 1500 1400 [参考答案](1)建立假设检验H:差值总体中位数为零H:差值总体中位数不为零1α=0.05(2)计算统计量见下表10名受试者针刺膻中穴前后痛阈编号针刺前针刺后差值秩次1 600 610 10 12 600 700 100 4.53 685 575 -110 -64 1050 600 -450 -105 900 600 -300 -8.56 1125 1425 300 8.57 1400 1350 -50 -28 750 825 75 39 1000 800 -200 -710 1500 1400 -100 -4.5合计 T+=17 T-=38T++T- = 17+38 = 55,总秩和(1)10(101)5522n n ++==, 计算准确无误T = min(T+,T-)=17。
(3)查表及结论现n=10,查T 界值表T 0.05(10)=8~47,T =17落在此范围内,所以P 0.05,按α=0.05水准,不拒绝H 0,针刺膻中穴前后痛阈值的差异无统计学意义。
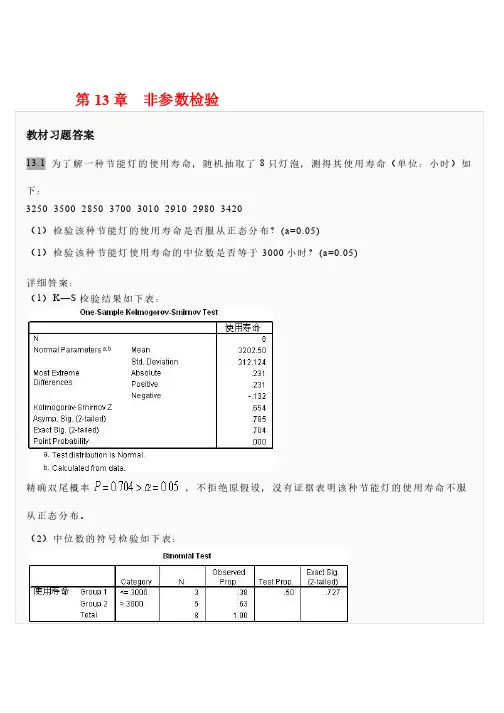
第13章非参数检验教材习题答案13.1 为了解一种节能灯的使用寿命,随机抽取了8只灯泡,测得其使用寿命(:小时时)如命(单单位:小下:3250 3500 2850 3700 3010 2910 2980 3420 (1)检验该种节能灯的使用寿命是否服从正态分布?(a=0.05) (1)检验该种节能灯使用寿命的中位数是否等于3000小时?(a=0.05) 详细答案:(1)K—S检验结果如下表:精确双尾概率,不拒绝原假设,没有证据表明该种节能灯的使用寿命不服从正态分布。
(2)中位数的符号检验如下表:精确的双尾概率为,不拒绝原假设,没有证据表明该种节能灯的使用寿命的实际中位数与3000有显著差异。
13.2 利用13.1题的数据,采用Wilcoxon符号秩检验该种节能灯使用寿命的中位数是否等于3000小时?(a=0.05) 详细答案:检验结果如下表精确的双尾概率,不拒绝原假设。
没有证据表明该种节能灯的使用寿命的实际中位数与3000有显著差异。
13.3 为分析股票的每股收益状况,在某证券市场上随机抽取10只股票,得到2005年和2006股收益年的每股收益数据如下表,采用Wilcoxon符号秩检验分析:2007年与2006年相比,每,每股是否有显著提高?(a=0.05) 股票代码2006年每股收益(元)2007年每股收益(元)1 0.12 0.26 2 0.95 0.87 3 0.20 0.24 4 0.02 0.12 5 0.05 0.13 6 0.56 0.51 7 0.31 0.35 8 0.25 0.42 9 0.16 0.37 10 0.06 0.05 详细答案:配对样本的Wilcoxon符号秩检验如下表:精确的单尾,拒绝,2006年与2005年相比每股收益有显著提高。
13.4 某种品牌的彩电在两个城市销售,其中在A城市有6个商场销售,在B城市有8个商场销售,下表是各商场一年的销售量(单位:台)。

统计软件实践数据(SPSS非参数部分)第一章单样本非参数检验1.1 2 检验例1.某企业大批连续生产某产品,要求不合格率不大于5%。
现从产品总体中,抽取100个进行检查,不合格品有12个,试以5%的显著性水平检验该批产品的不合格率是否为5%。
例2.某金融机构的货款偿还类型有A、B、C、D四种,各种的预期偿还率为80%、12%、7%和1%。
在一段时间的观察记录中,A型按时偿还的有380笔,B型有69笔,C型有43笔,D型有8笔。
问在5%显著性水平上,这些结果与预期的是否一致。
例3.两种不同牌号的茶哪个更好。
今有30人组成的品茶专家组,对A、B两种不同牌号的茶进行6种味道的检验。
凡专家认为优者被记录下来,如下表示。
1.2 K-S 检验例1.《数理统计与管理》论文作者服从洛特卡分布。
例2.公共交通设施适合性的研究——公共汽车到达时间是否服从正态分布公共汽车按计划每15分钟通过一个商店旁。
然而,由于交通条件,乘客数目等的影响,汽车实际到达的时间有很大的不同。
通过一天的随机观察,获得的数据如下表示。
比计划提前到达的为负值,取大的整数,如提前一分10秒到达,记为-1;比计划晚到的为正值,也取大的整数,如迟到1分10秒,记作+2。
公共汽车到达时间是否服从3σ=的正态分布。
例3.某大街在一年内的交通事故按星期日、星期一、星期二、星期六分为七类进行统计,记录如下表。
试问:事故的发生是否与星期几有关?1.3 符号检验例1.广告对商品促销是否起作用。
例2.生产过程是否需要调整某企业生产一种钢管,规定和度的中位数为10米。
现随机地从正在生产的生产线上选取10根进行测量,结果为:9.8, 10.1, 9.7, 9.9, 9.8, 10.0, 9.7, 10.0, 9.9, 9.8例3.领导者的领导水平是可以训练的为验证领导者是可以训练的,根据人的聪明程度、人品、受教育状况等,随机抽取出12个人配对成6对,每对中有一人随机选择受训,记作T,另一人则不受训记作经过一段时间后,按被设计好的问题评价他们的领导水平,结果如下表示。

非参数考试题及答案一、单项选择题(每题2分,共10题)1. 非参数统计方法主要处理的是:A. 正态分布数据B. 非正态分布数据C. 离散型数据D. 连续型数据答案:B2. 斯皮尔曼等级相关系数适用于:A. 正态分布数据B. 非正态分布数据C. 有序分类数据D. 有序连续数据答案:B3. 曼-惠特尼U检验用于比较:A. 两个独立样本的均值B. 两个独立样本的中位数C. 两个配对样本的均值D. 两个配对样本的中位数答案:B4. 克鲁斯卡尔-瓦利斯检验用于:A. 单样本方差分析B. 双样本方差分析C. 多样本方差分析D. 配对样本方差分析答案:C5. 弗里德曼检验适用于:A. 单因素方差分析B. 双因素方差分析C. 多因素方差分析D. 配对样本方差分析答案:D6. 威尔科克森符号秩检验用于:A. 两个独立样本的比较B. 两个配对样本的比较C. 多个独立样本的比较D. 多个配对样本的比较答案:B7. 非参数检验中,不需要假设数据分布的是:A. t检验B. 方差分析C. 卡方检验D. 克鲁斯卡尔-瓦利斯检验答案:D8. 斯皮尔曼等级相关系数的取值范围是:A. -1到1B. 0到1C. -1到0D. 0到-1答案:A9. 以下哪个检验不是非参数检验:A. 曼-惠特尼U检验B. 克鲁斯卡尔-瓦利斯检验C. 弗里德曼检验D. 单样本t检验答案:D10. 非参数检验中,用于比较两个独立样本的秩次差异的是:A. 威尔科克森符号秩检验B. 弗里德曼检验C. 克鲁斯卡尔-瓦利斯检验D. 曼-惠特尼U检验答案:D二、多项选择题(每题3分,共5题)1. 以下哪些是非参数检验:A. 曼-惠特尼U检验B. 单样本t检验C. 克鲁斯卡尔-瓦利斯检验D. 威尔科克森符号秩检验答案:ACD2. 以下哪些检验适用于两个独立样本的比较:A. 曼-惠特尼U检验B. 威尔科克森符号秩检验C. 弗里德曼检验D. 克鲁斯卡尔-瓦利斯检验答案:AD3. 以下哪些检验适用于多个独立样本的比较:A. 威尔科克森符号秩检验B. 克鲁斯卡尔-瓦利斯检验C. 弗里德曼检验D. 曼-惠特尼U检验答案:BC4. 以下哪些检验适用于配对样本的比较:A. 单样本t检验B. 威尔科克森符号秩检验C. 弗里德曼检验D. 曼-惠特尼U检验答案:BC5. 以下哪些检验不需要假设数据的分布:A. 单样本t检验B. 曼-惠特尼U检验C. 克鲁斯卡尔-瓦利斯检验D. 威尔科克森符号秩检验答案:BCD三、简答题(每题5分,共2题)1. 请简述非参数检验与参数检验的主要区别。

第十一章非参数检验第一节符号检验符号检验的方法·符号检验的特点和作用第二节配对符号秩检验配对符号秩检验的方法·配对符号秩检验的效力第三节秩和检验秩和检验的方法·秩和检验的近似第四节游程检验游程的概念·游程检验的方法·差符号游程检验第五节累计频数检验累计频数检验的方法·累计频数检验的应用一、填空1.非参数检验,泛指“对分布类型已知的总体进行参数检验”()的所有检验方法。
2.符号检验的零假设就是配对观察结果的差平均起来等于()。
3.理论研究表明,对于配对样本非正态分布的差值d,()是最佳检验。
4.秩和检验检验统计量U是U1和U2中较()的一个。
5.秩尺度之统计量的均值和标准差只取决于()。
6.()常被用作经验分布与理论分布的比较。
7.绝对值相等的值,应将它们的秩()。
8.符号检验,在分布自由检验中称为()。
9.符号检验和配对符号秩检验,都只适用于()样本。
10.数据序列ABBABAAABABBABBAAAAAB的总游程数是()二、单项选择1.下列检验中,不属于非参数统计的方法的是()。
A总体是否服从正态分布 B 总体的方差是否为某一个值C 样本的取得是否具有随机性D 两组随机变量之间是否相互独立2.下列情况中,最适合非参数统计的方法是()。
A反映两个大学新生成绩的差别B 反映两个大学新生家庭人均收入的差别C 反映两个大学三年级学生对就业前景的看法差别D反映两个大学在校生消费水平的差别3.不属于非参数检验的是()。
A符号检验B游程检验C累计频数检验 D F检验4.在累计频数检验中,卡方的自由度为()。
A n1B 2C n2D n1+n25.配对符号秩检验的效力( )。
A 小于符号检验B 大于t 检验C 介于符号检验与t 检验之间D 无法与符号检验及t 检验比较 6.如果我们说非参数检验的效力是80%,下列哪种解释正确。
( )A 如果用参数检验需要100个数据,那么在同等的检验效力下,非参数检验只要80个数据;B 如果用非参数检验需要100个数据,那么在同等的检验效力下,参数检验只要80个数据;C 如果用参数检验需要100个数据,那么在同等的检验效力下,非参数检验只要20个数据;D 如果用非参数检验需要100个数据,那么在同等的检验效力下,参数检验只要20个数据;7.对于秩和检验,U 1、U 2和n 1、 n 2的关系是( )。

非参数统计试题
一、试比较参数统计与非参数统计的区别和联系。
(15)
二、请你结合实际谈谈非参数统计的应用。
(15)
三、试验者把一只老鼠放入一个有两扇门的笼子里,并且把门都关上,一扇涂红色一扇涂
蓝
色,然后给老鼠播放一段音乐,再同时打开两扇门,记录老鼠逃出选择的门的颜色,重复了10次,发现有7次从红色门中出来,他的结论是:此时老鼠更喜欢红色。
他同时做另一个试验向10只老鼠注射某种药物,5分钟后有7只死亡,他断定这个结果具有偶然性,即药物不具有危险性。
试分析他的结论的合理性,如果是你,你怎样分析这一问题?可以通过适当计算来说明你的结论。
(20)
四、下列数据是从某个总体中,随机抽取的,数据如下:
34 38 56 23 41 52 37 53 46 37 29 48 35 43试问利用这一组数据我们能分析什么?(不需要计算,只说明怎样分析);若还有一组数据,如:38 45 27 34 46 63 34 48 30 43,我们又如何分析他们?写出你的分析思路。
(20)
五、下面是关于非参数统计的一段文献,试叙述其主要意思(30)。

练习题1.随机从四个班级中抽取一些同学数学成绩进行比较,看不同教师的教学效果是否一致。
观测1 观测2 观测3 观测483 91 112 7891 90 105 8294 81 91 8189 83 93 7089 84 103 79103 83 95 8191 88 94 8092 91 8190 89842.把3个减肥计划分配给了12名志愿者,志愿者们被分配到哪个计划是随机的,总共有36位志愿者,假设他们是来自可能要试用一种减肥计划人群的随机样本。
检验零假设:在3种计划下减肥量的概率分布没有差别。
每个人减掉的重量(单位:千克)结果如下:3.以下数据是某棒球比赛中两队中出现盗垒的个数,试问两队中盗垒的个数是否存在显著差异。
(1)使用符号检验方法;(2)使用Wilcoxon符号秩检验;(3)哪种方法最好,为什么?队伍所在位置一队二队1 91 812 46 513 108 634 99 515 110 466 105 457 191 668 57 649 34 9010 81 285.为了比较属同一类的4种不同食谱的营养效果,将25只老鼠随机地分成4组,每组分别是8只,4只,7只和6只,各采用食谱甲,乙,丙,丁喂养。
假设其他条件均保持相同,12周后测得体重增加量如下表所示。
对于α=0.05,检验各食谱的营养效果是否有显著差异。
单位:cm食谱体重增加量/克甲164 190 203 205 206 214 228 257 乙185 197 201 231丙187 212 215 220 248 265 281丁202 204 207 227 230 2766.假设我们观察15个吸烟者接受戒烟宣传前后的变化,获得2个差为0,13个差不为0,其中11个正号,2个负号。
(1)试在0.05的显著性水平上进行检验戒烟宣传是否收到明显成效;(2)若10个为正号,3个为负号,检验结果如何?7.从甲、乙两市初中生中分别随机抽取一部分学生并测量他们的身高,结果如下,请用中位数检验法检测两市初中学生的身高是否有显著差异。
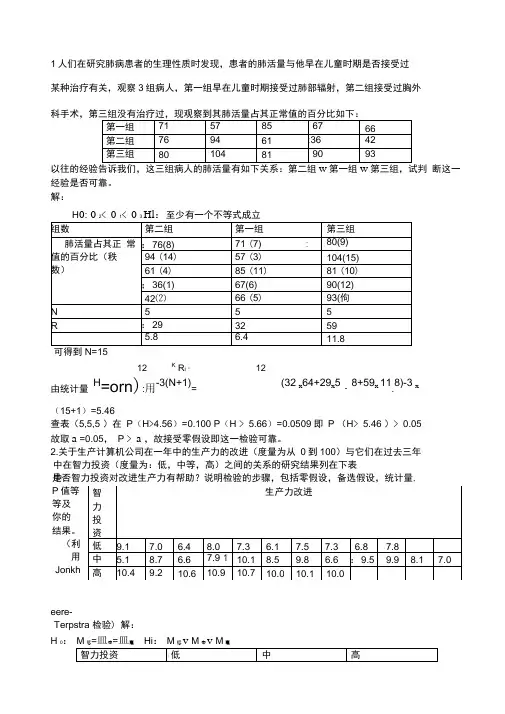
1人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过 某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外 科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:以往的经验告诉我们,这三组病人的肺活量有如下关系:第二组w 第一组w 第三组,试判 断这一经验是否可靠。
解:H2< 1< 3 至少有一个不等式成立可得到N=1512KR i 212由统计量H=orn ):用-3(N+1)=(32 x 64+29x 5・8+59x 11.8)-3 x(15+1)=5.46查表(5,5,5 )在 P (H >4.56)=0.100 P (H > 5.66)=0.0509 即 P (H > 5.46 )> 0.05 故取a =0.05, P > a ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从 0到100)与它们在过去三年eere-Terpstra 检验) 解:H 0:低中高 低中高中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中: 是否智力投资对改进生产力有帮助?说明检验的步骤,包括零假设,备选假设,统计量, P 值等 等及 你的 结果。
(利 用 JonkhU 2=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U !a =10X 8=80123=12+9+12+12+12+11+12+11=89 J 八 U j =82.5+80+89=251.5i 」kJ -( N 2 -送』i 2) , 4N (2N 3) :n i 2(2n i 3) 1 72求得 Z=3.956 ①(3.956)=0.9451取a =0.05 , P > a ,故接受原假设,认为智力投资对改进生产力有帮助大样本近似Z=〜N ( 0,1 )。

非参数统计(第二版)习题R程序P37.例2.1build.price<-c(36,32,31 ,25,28,36,40,32,41,26,3 5,35,32,87,33,35);build .pricehist(build.price,freq=FA LSE)#直方图lines(density(build.pric e),col="red")#连线#方法一:m<-mean(build.price); m#均值D<-var(build.price)#方差SD<-sd(build.price)#标准差St=(m-37)/(SD/sqrt(len gth(build.price)));t#t统计量计算检验统计量t=[1] -0.1412332 #方法二:t.test(build.price-37)#课本第38页例2.2binom.test(sum(build.p rice<37),length(build.p rice),0.5)#课本40页例2.3P<-2*(1-pnorm(1.96,0, 1));P[1] 0.04999579P1<-2*(1-pnorm(0.790 6,0,1));P1[1] 0.4291774> 例2.4>p<-2*(pnorm(-1.96,0,1 ));p[1] 0.04999579>>p1<-2*(pnorm(-0.9487 ,0,1));p1[1] 0.3427732例2.5(P45)scores<-c(95,89,68,90, 88,60,81,67,60,60,60,6 3,60,92,60,88,88,87,60,73,60,9 7,91,60,83,87,81,90);le ngth(scores)#输入向量求长度ss<-c(scores-80);sst<-0t1<-0for(i in 1:length(ss)){ if (ss[i]<0) t<-t+1#求小于80的个数else t1<-t1+1求大于80的个数}t;t1> t;t1 [1] 13[1] 15binom.test(sum(scores <80),length(scores),0.7 5)p-value =0.001436<0.01Cox-Staut趋势存在性检验P47例2.6year<-1971:2002;year length(year)rain<-c(206,223,235,26 4,229,217,188,204,182, 230,223,227,242,238,207,208,2 16,233,233,274,234,22 7,221,214,226,228,235,237,243,2 40,231,210)length(rain)#(1)该地区前10年降雨量是否变化?t1=0if(client[i]==client[i+1]) t1<-t1else t1<-t1+1}R<-t1+1;R#=12#find rejection region (不写)rl<-1+2*n1*n0/(n1+n 0)*(1-1.96/sqrt(n1+n0 ));rlru<-2*n1*n0/(n1+n0) *(1+1.96/sqrt(n1+n0)) ;ru#=15.33476(课本为ru=17)例2.9shuju39<-data.frame(r ead.table("SHUJU39.txt",header =TRUE));shuju39 attach(shuju39) sum.a=0sum.b=0sum.c=0 for (i in 1:length(id)){ if (pinzhong[i]=="A") sum.a<-sum.a+chanlia ng[i]else if(pinzhong[i]=="B") sum.b<-sum.b+chanlia ng[i]elsefuhao<-sum.c<-sum.c+ chanliang[i]}sum.a;sum.b;sum.cma<-sum.a/4mb<-sum.b/4mc<-sum.c/4ma;mb;mcfuhao<-rep("a",12);fuh aofor (i in 1:length(id)){ if (pinzhong[i]=="A" & ((chanliang[i]-ma)>0)) fuhao[i]<-"+"else if(pinzhong[i]=="B" &((chanliang[i]-mb)>0)) fuhao[i]<-"+"else if(pinzhong[i]=="C" & ((chanliang[i]-mc)>0)) fuhao[i]<-"+"else fuhao[i]<-"-"}fuhao#利用上题编程解决检验的随机性n<-length(fuhao);nn1<-sum(fuhao=="+") ;n1n0<-n-n1;n0t1<-0for (i in1:(length(fuhao)-1)){ if(fuhao[i]==fuhao[i+1]) t1<-t1else t1<-t1+1} R<-t1+1;R#find rejection region rl<-1+2*n1*n0/(n1+n0)*(1-1.96/sqrt(n1+n0 ));rlru<-2*n1*n0/(n1+n0) *(1+1.96/sqrt(n1+n0)) ;ru例2.10(P52)library(quadprog)# 不存在叫‘quadprog’这个名字的程辑包library(zoo)# 不存在叫‘zoo’这个名字的程辑包library(tseries)# 不存在叫‘tseries’这个名字的程辑包run1=factor(c(1,1,1,0,r ep(1,7),0,1,1,0,0,rep(1, 6),0,rep(1,4),0,rep(1,5),rep(0,4),rep( 1,13)));run1y=factor(run1)runs.test(y)# 错误: 没有"runs.test"这个函数Wilcoxon符号秩检验W+在零假设下的精确分布#下面的函数dwilxonfun 用来计算W+分布密度函数,即P(W+=x)的一个参考程序!dwilxonfun=function(N ){a=c(1,1) #when n=1 frequency of W+=1 or o n=1pp=NULL #distribute of all size from 2 to N aa=NULL #frequency of all size from 2 to Nfor (i in 2:N){t=c(rep(0,i),a)a=c(a,rep(0,i))+tp=a/(2^i)#density of Wilcox distribut when size=N }p}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);y#计算P(W+=x)中的x取值的R参考程序!!dwilxonfun=function(N ){a=c(1,1) #when n=1 frequency of W+=1 or o n=1pp=NULL #distribute of all size from 2 to N aa=NULL #frequency of all size from 2 to Nfor (i in 2:N){t=c(rep(0,i),a)a=c(a,rep(0,i))+tp=a/(2^i)#density of Wilcox distribut when size=N }a}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);lengt h(y)-1hist(y,freq=FALSE) lines(density(y),col="re d")例2.12(P59)ceo<-c(310,350,370,37 7,389,400,415,425,440, 295,325,296,250,340,298,3 65,375,360,385);length (ceo)#方法一wilcox.test(ceo-320)#方法二ceo.num<-sum(ceo>32 0);ceo.numn=length(ceo) binom.test(ceo.num,n,0 .5)例2.13(P61)a<-c(62,70,74,75,77,80 ,83,85,88)walsh<-NULLfor (i in1:(length(a)-1)){for (j in(i+1):length(a)){ walsh<-c(walsh,(a[i]+a [j])/2)}}walsh=c(walsh,a)NW=length(walsh);NW median(walsh)2.5单组数据的位置参数置信区间估计(P61)例2.14‘stu<-c(82,53,70,73,103 ,71,69,80,54,38,87,91,62,75,6 5,77);stualpha=0.05rstu<-sort(stu);rstu conff<-NULL;conffn=length(stu);nfor(i in 1:(n-1)){for (j in (i+1):n){ conf=pbinom(j,n,0.5)-p binom(i,n,0.5)if(conf>1-alpha){conff<-c(conff,i,j,conf)}}}confflength(conff) min<-103-38;minc<-seq(1,(length(conff) -1),3);cfor(i in c){col<-c(rstu[conff[i]],rst u[conff[i+1]],conff[i+2 ])min1<-rstu[conff[i+1]] -rstu[conff[i]]if(min1<min){min<-min 1;l<-i}print(col)}col1<-c(rstu[conff[l]],r stu[conff[l+1]],conff[l+ 2]);col1min例2.14“stu<-c(82,53,70,73,103 ,71,69,80,54,38,87,91,62,75,6 5,77);stualpha=0.05n=length(stu);nconf=pbinom(n,n,0.5)-pbinom(0,n,0.5);conf for(k in 1:n){conf=pbinom(n-k,n,0.5) -pbinom(k,n,0.5)if(conf<1-alpha){loc=k-1;break}}print(loc)(剩余的例题参考程序在课本)3.6正态记分检验例2.18baby1<-c(4,6,9,15,31,3 3,36,65,77,88)baby=(baby1-34);baby baby.mean=mean(baby );baby.mean例2.18qiuzhi<-function(x){n=length(x)a=rep(2,n)for (i in 1:n){a[i]=sum(x<=x[i]) }a}fuhao<-function(x,y){ n=length(x)sgn=rep(2,n)for(i in 1:n){if (x[i]>y)sgn[i]=1else if (x[i]==y)sgn[i]=0elsesgn[i]=-1}sgn}n1<-length(baby) babyzhi=qiuzhi(baby)q=(n1+1+babyzhi)/(2* n1+2)babysgn<-fuhao(baby,3 4)babysgn=sign(baby1-3 4);babysgns=qnorm(q,0,1)W<-t(s)%*%babysgn; Wsd<-sum((s*babysgn)^ 2);sdT=W/sd;T2.7分布的一致性检验例2.19shuju1<-data.frame(m onth=c(1:6), customers=c(27,18,15, 24,36,30));shuju1 attach(shuju1)n<-sum(customers);n expect<-rep(1,6)*(1/6) *n;expect x.squ=sum((customers-expect)^2)/25;x.squ#方法一value<-qchisq(1-0.05,le ngth(customers)-1);val ue#方法二pvalue<-1-pchisq(x.squ ,length(customers)-1);p value例2.20shuju2<-data.frame(ch ongshu=c(0:6), zhushu=c(10,24,10,4,1, 0,1));shuju2attach(shuju2)n=sum(zhushu);n lamda<-sum(chongshu *zhushu)/n;lamdap<-dpois(chongshu,lam da);pn*px.squ=sum((zhushu^2) /(n*p))-n;x.squ#方法一value<-qchisq(1-0.05,le ngth(zhushu)-1);value#方法二pvalue<-1-pchisq(x.squ ,length(zhushu)-1);pval ue例2.21shuju3<-c(36,36,37,38, 40,42,43,43,44,45,48,4 8,50,50,51,52,53,54,54,5 6,57,57,57,58,58,58,58, 58,59,60,61,61,61,62,6 2,63,63,65,66,68,68,70, 73,73,75);shuju3n=length(shuju3)n0=sum(shuju3<30);n 0n1=sum(shuju3>30 & shuju3<=40);n1 n2=sum(shuju3>40 & shuju3<=50);n2n3=sum(shuju3>50 & shuju3<=60);n3n4=sum(shuju3>60 & shuju3<=70);n4n5=sum(shuju3>70 & shuju3<=80);n5n6=sum(shuju3>80);n 6nn<-c(n0,n1,n2,n3,n4,n 5,n6);nn #计算45位学生体重分类的频数!shuju3.mean=mean(sh uju3);shuju3.mean shuju3.var=var(shuju3) ;shuju3.varshuju3.sd=sd(shuju3);s huju3.sde0=pnorm(30,shuju3.m ean,shuju3.sd)e1=pnorm(40,shuju3.m ean,shuju3.sd)-pnorm( 30,shuju3.mean,shuju3. sd)e2=pnorm(50,shuju3.m ean,shuju3.sd)-pnorm( 40,shuju3.mean,shuju3. sd)e3=pnorm(60,shuju3.m ean,shuju3.sd)-pnorm( 50,shuju3.mean,shuju3. sd)e4=pnorm(70,shuju3.m ean,shuju3.sd)-pnorm( 60,shuju3.mean,shuju3. sd)e5=pnorm(80,shuju3.m ean,shuju3.sd)-pnorm( 70,shuju3.mean,shuju3. sd)e6=1-pnorm(80,shuju3. mean,shuju3.sd)e=c(e0,e1,e2,e3,e4,e5, e6);eee=n*c(e0,e1,e2,e3,e4, e5,e6);eex.squ=sum((nn^2)/(ee ))-n;x.squ#方法一value<-qchisq(1-0.05,le ngth(ee)-1);value #方法二pvalue<-1-pchisq(x.squ ,length(ee)-1);pvalue 例2.22healthy<-c(87,77,92,68 ,80,78,84,77,81,80,80,7 7,92,86,76,80,81,75,77,72,81,9 0,84,86,80,68,77,87,76, 77,78,92,75,80,78);healthyks.test(healthy,pnorm,8 0,6)第三章#Brown_Mood中位数#Brown-Mood中位数检验程序BM.test<-function(x,y,a lt){xy<-c(x,y)md.xy<-median(xy) #利用中位数的检验#md.xy<-quantile(xy,0.25) #利用p分位数的检验t<-sum(xy>md.xy)lx<-length(x)ly<-length(y)lxy<-lx+lyA<-sum(x>md.xy) if (alt=="greater"){w<-1-phyper(A,lx,ly,t) }else if (alt=="less"){w<-phyper(A,lx,ly,t)}conting.table=matrix(c( A,lx-A,lx,t-A,ly-(t-A),ly,t ,lxy-t,lxy),3,3)<-c("X","Y","X +Y") <-c(">MXY"," <MXY","TOTAL")dimnames(conting.tabl e)<-list(, )list(contingency.table= conting.table,p.vlue=w) }例3.2X<-c(698,688,675,656, 655,648,640,639,620) Y<-c(780,754,740,712, 693,680,621)#方法一:BM.test(X,Y,"less")#方法二:XY<-c(X,Y)md.xy<-median(XY)t<-sum(XY>md.xy)lx<-length(X)ly<-length(Y)lxy<-lx+lyA<-sum(X>md.xy)#没有修正时的情形pvalue1<-pnorm(A,lx*t /(lx+ly),sqrt(lx*ly*t*(lx+ly-t)/( lx+ly)^3));pvalue1#修正时的情形pvalue2<-pnorm(A,lx*t /(lx+ly)-0.5,sqrt(lx*ly*t*(lx+ly-t)/( lx+ly)^3));pvalue2 3.2、Wilcoxon-Mann-Whitne y秩和检验#求两样本分别的秩和的程序.Qiuzhi<-function(x,y){ n1<-length(y)yy<-c(x,y)wm=0for(i in 1:n1){ wm=wm+sum(y[i]>yy, 1)}wm}例3.3weight.low=c(134,146, 104,119,124,161, 107,83,113,129,97,123 )m=length(weight.low) weight.high=c(70,118, 101,85,112,132,94)n=length(weight.high) #方法一:wy<-Qiuzhi(weight.low ,weight.high)##wy=50 wxy<-wy-n*(n+1)/2;w xy#=22mean<-m*n/2var<-m*n*(m+n+1)/1 2pvalue<-1-2*pnorm(wx y,mean-0.5,var);pvalue #方法二wilcox.test(weight.high ,weight.low)例3.4Mx-My的R参考程序:x1<-c(140,147,153,160 ,165,170,171,193)x2<-c(130,135,138,144 ,148,155,168)n1<-length(x1)n2<-length(x2)th.hat<-median(x2)-me dian(x1)B=10000Tboot=c(rep(0,1000)) #vector of length Bootstrapfor (i in 1:B){ xx1=sample(x1,5,T)#sample of size n1 with replacement from x1xx2=sample(x2,5,T)#sample of size n2 with replacement from x2 Tboot[i]=median(xx2)-median(xx1)}th<-median(Tboot);th se=sd(Tboot) Normal.conf=c(th+qnor m(0.025,0,1)*se,th-qno rm(0.025,0,1)*se);Nor mal.confPercentile.conf=c(2*th-quantile(Tboot,0.975),2 *th-quantile(Tboot,0.025));Percenti le.confProvotal.conf=c(quantil e(Tboot,0.025),quantile (Tboot,0.975));Provotal .confth.hat3.3、Mood方差检验qiuzhi<-function(x,y){ xy<-c(x,y)zhi<-NULLfor (i in 1:length(x)){ zhi<-c(zhi,sum(x[i]>=x y))}zhi}引例:x1<-c(48,56,59,61,84,8 7,91,95)x2<-c(2,22,49,78,85,89 ,93,97)zhi_x1=qiuzhi(x1,x2);z hi_x1#zhi_x2=qiuzhi(x2,x1); zhi_x2#var_x1=var(x1);var_x 1#var_x2=var(x2);var_x 2 m=length(x1);mn=length(x2);nmean_R=(m+n+1)/2; mean_Rmean1=m*(m+n+1)*( m+n-1)/12;mean1var1=m*n*(m+n+1)*( m+n+2)*(m+n-2)/180; var1M1=sum((zhi_x1-mean _R)^2);M1p_value=2*pnorm(M1, mean1-0.5,sqrt(var1)) p_value例3.5X<-c(4.5,6.5,7,10,12) Y<-c(6,7.2,8,9,9.8)zhi_X=qiuzhi(X,Y);zhi_ Xm=length(X);mn=length(Y);nmean_R=(m+n+1)/2; mean_Rmean2=m*(m+n+1)*( m+n-1)/12;mean2var2=m*n*(m+n+1)*( m+n+2)*(m+n-2)/180; var2M2=sum((zhi_X-mean_ R)^2);M2#方法一:查附表9#方法二:p_value=2*(1-pnorm( M2,mean2-0.5,sqrt(var 2)))p_value#方法三Z=1/(sqrt(var2))*(M2-mean2+0.5);Z3.4、Moses方差检验qiuzhi<-function(x,y){ xy<-c(x,y)zhi<-NULLfor (i in1:length(x)){ zhi<-c(zhi,sum(x[i]>=x y))}zhi}例3.6x1<-c(8.2,10.7,7.5,14.6 ,6.3,9.2,11.9,5.6,12.8,5.2,4.9,13.5)m1=length(x1);m1x2<-c(4.7,6.3,5.2,6.8,5. 6,4.2,6.0,7.4,8.1,6.5)m2=length(x2);m2A<-matrix(x1,ncol=3); A#随机分组a1=sample(x1,3,F)xx2=NULLfor(i in 1:m1){if(sum(a1==x1[i])==0) xx2=c(xx2,x1[i])}a2=sample(xx2,3,F)xx3=NULLfor(i in 1:(m1-3)){if(sum(a2==xx2[i])== 0) xx3=c(xx3,x1[i])}a3=sample(xx3,3,F)x11=sum((A[1,]-mean( x1))^2);x11x12=sum((A[2,]-mean( x1))^2);x12x13=sum((A[3,]-mean( x1))^2);x13x14=sum((A[4,]-mean( x1))^2);x14SSA<-c(x11,x12,x13,x1 4);SSAB<-matrix(x2[1:9],ncol =3);By11=sum((B[1,]-mean( x2))^2);y11y12=sum((B[2,]-mean( x2))^2);y12 y13=sum((B[3,]-mean( x2))^2);y13SSB<-c(y11,y12,y13);S SBzhi_SSA=qiuzhi(SSA,SS B);zhi_SSAzhi_SSB=qiuzhi(SSB,SS A);zhi_SSBS=sum(zhi_SSA);STM=S-4*(4+1)/2;TM #方法一(查附表4)拒绝域C=(TM<W(0.025,m1,m 2)或者TM>W(0.975,m1,m2)) 其中W(0.975,m1,m2)=m1* m2-W(0.025,m1,m2). #方法二(Wilcoxon秩和检验)wilcox.test(SSA,SSB) #方法二(Mann-Whitney 秩和检验)m=length(SSA);mn=length(SSB);n mean_AB=m*n/2;mea n_ABvar_AB=m*n*(m+n+1) /12;var_ABp_value=1-pnorm(S,me an_AB,sqrt(var_AB));p_ value第四章4.1、试验设计和方差分析的基本概念回顾#R软件中单因素方差分析的函数例4.1#方法一:****Analysis of Variance Model ****y<-c(2.0,1.4,2.0,2.8,2.4 ,1.9,1.8,2.5,2.0,1.5,2.1, 2.2);y lever<-c("B","A","C","C ","B","A","B","C","A","A ","C","B")x<-factor(lever);xxy<-data.frame(y,x) attach(xy)aov(formula=y~x,data =xy)aov.xy<-aov(formula=y ~x,data=xy) summary(aov.xy)#方法二:x1<-c(1.4,1.9,2.0,1.5) x2<-c(2.0,2.4,1.8,2.2) x3<-c(2.6,2.8,2.5,2.1) y<-c(x1,x2,x3);yy.mean<-mean(y);y.me anssT<-sum((y-y.mean)^ 2);ssT #计算总的平方和x1.mean<-mean(x1)x2.mean<-mean(x2)x3.mean<-mean(x3) sse<-sum(sum((x1-x1. mean)^2),sum((x2-x2.mean)^2), sum((x3-x3.mean)^2)) ;sse #计算误差平方和sst<-ssT-sse;sst #计算组间平方和F<-(sst/2)/(sse/(lengt h(y)-3));F #计算方差分析的F检验统计量#临界值的计算value<-qf(0.95,2,length (y)-3);value#计算p-value值p.value<-1-pf(8,2,lengt h(y)-3);p.value表4.5xueye<-c(8.4,9.4,9.8,1 2.2,10.8,15.2,9.8,14.4,8.6,9 .8,10.2,9.8, 8.8,9.8,8.9,12.0,8.4,9.2, 8.5,9.5);xueyesst1<-sum((xueye-mea n(xueye))^2);sst1a=matrix(xueye,ncol=5 );aquzu<-apply(a,2,sum); quzuchuli<-apply(a,1,sum);c hulik=5b=4ssb=1/4*sum(quzu^2) -sum(quzu)^2/(k*b);ss bsst=1/5*sum(chuli^2)-sum(chuli)^2/(k*b);sst sse=sst1-ssb-sst;sse mssb=ssb/(k-1);mssb msst=sst/(b-1);msst msse=sse/(k*b-k-b+1) ;msseF1=mssb/msse;F1F2=msst/msse;F2value1=qf(1-0.05,k-1,k *b-k-b+1)value2=qf(1-0.05,b-1,k *b-k-b+1)例4.3qiuzhi<-function(w,x,y, z){xy<-c(w,x,y,z)zhi<-NULLfor (i in1:length(w)){zhi<-c(zhi,sum(w[i]>= xy))}zhi}a<-c(80,203,236,252,2 84,368,457,393)b<-c(133,180,100,160) c<-c(156,295,320,448, 465,481,279)d<-c(194,214,272,330, 386,475)azhi=qiuzhi(a,b,c,d);az hibzhi=qiuzhi(b,a,c,d);bz hiczhi=qiuzhi(c,a,b,d);czh idzhi=qiuzhi(d,a,b,c);dz hiH=12/(n*(n+1))*(sum (azhi)^2/length(a)+su m(bzhi)^2/length(b) +sum(czhi)^2/length(c )+sum(dzhi)^2/length( d))-(3*(n+1))方法一:value=qchisq(1-0.05,3) ;value方法二:pvalue=1-pchisq(H,3);p valuemean=c(mean(a),mean (b),mean(c),mean(d))#两两比较的程序bjiao=function(azhi,bzh i,czhi,dzhi){{n=length(c(azhi,bzhi,c zhi,dzhi))av=sum(azhi)/length(a zhi)bv=sum(bzhi)/length(b zhi)se=sqrt(n*(n+1)/12*( 1/length(azhi)+1/lengt h(bzhi)))d=abs(av-bv)dab=d/sehuizong=c(d,se,dab,qn orm(1-0.05,0,1))}huizong}bjiao(azhi,bzhi,czhi,dzhi ) bjiao(czhi,dzhi,azhi,bzhi )4.3、Jonckheere-Terpstra检验例4.5x=c(125,136,116,101,1 05,109)y=c(122,114,131,120,1 19,127)z=c(128,142,128,134,1 35,131,140,129)xm=mean(x);xmym=mean(y);ymzm=mean(z);zmg=c(rep(1,6),rep(2,6),r ep(3,8))tapply(c(x,y,z),g,media n)JT.test(data=t(c(x,y,z)) ,class=g)Wij<-function(x,y){n1=length(y)zhiij<-0for(i in 1:n1){zhiij=zhiij+sum(x<y[i]) +sum(x==y[i])/2}zhiij}w12=Wij(x,y);w12w13=Wij(x,z);w13w23=Wij(y,z);w23#方法一:通过查表决策!# W=sum(w12,w13,w23) ;W#方法二:通过中心极限定律决策!#N=length(c(x,y,z))n1=length(x)n2=length(y)n3=length(z) E=(N^2-sum(n1^2,n2 ^2,n3^2))/4;E #计算J的数学期望#f1=function(n){f=n^2* (2*n+3)}Var=(f1(N)-sum(f1(n1), f1(n2),f1(n3)))/72;Var sd.Var=sqrt(Var);sd.Var #计算J的方差和标准差# z1=(W-E)/sd.Var;z1#可以通过拒绝域来决策# pvalue=2*(1-pnorm(z,0 ,1));pvalue #可以通过pvalue值来决策#例4.6jie=function(x,y){{ jiedian<-NULLshuju<-NULLxy<-c(x,y)y1<-unique(y)for (i in1:length(y1)){if(sum(xy==y1[i])>1){jiedian<-c(jiedian,sum (xy==y1[i]))shuju<-c(shuju,y1[i])}}j=c(jiedian,shuju)#shuju 输出是那些数据打结#}j}a=c(40,35,38,43,44,41) b=c(38,40,47,44,40,42) c=c(48,40,45,43,46,44) jie12=jie(a,b);jie12jie13=jie(a,c);jie13jie23=jie(b,c);jie23#例4.7(P128)qiuzhi=function(x){ n1=length(x)n2=length(unique(x)) zhi=NULLif (n1==n2){for (i in 1:n1){ zhi=c(zhi,sum(x<=x[i]) )}}else{for (i in 1:n1){ zhi=c(zhi,mean(sum(x <x[i],1):sum(x<=x[i])) )}}zhi}jiedian=function(x1){ n1=length(x1)x2=unique(x1)n2=length(x2)jie=NULLfor(i in 1:n2){n=sum(x1==x2[i])if (n>1)jie=c(jie,n)}jie}a1=c(85,82,82,79)a2=c(87,75,86,82)a3=c(90,81,80,76)a4=c(80,75,81,75)zhi1=qiuzhi(a1);zhi1 zhi2=qiuzhi(a2);zhi2 zhi3=qiuzhi(a3);zhi3 zhi4=qiuzhi(a4);zhi4a1=t(matrix(c(zhi1,zhi2 ,zhi3,zhi4),ncol=4));a1 b1=apply(a1,2,sum);b1 b=4 k=4Q=12/(b*k*(k+1))*su m(b1^2)-3*b*(k+1);Q jie1=jiedian(a1);jie1 jie2=jiedian(a2);jie2 jie3=jiedian(a3);jie3 jie4=jiedian(a4);jie4 jien=c(jie1,jie2,jie3,jie 4);jienjienn=sum(jien^3-jien) ;jiennt1=b*k*(k^2-1);t1Qc=Q/(1-jienn/t1);Qc5.3、Fisher精确性检验setwd("")getwd()例5.3medicine<-matrix(c(8,2 ,7,23),,2,byrow=T) medicinefisher.test(medicine) chisq.test(medicine)。

非参数统计真题答案及解析统计学作为一门重要的学科,对于量化研究各种现象和问题具有重要的作用。
在统计学中,参数统计和非参数统计是两个重要的分支。
参数统计是指根据总体的参数,通过样本数据对总体进行估计或假设检验。
而非参数统计则是在对总体参数没有明确假设的情况下,通过对样本数据的分析来进行统计推断。
本文将通过一些非参数统计的真题来深入讨论非参数统计的方法和应用。
一、Wilcoxon符号秩检验Wilcoxon符号秩检验是一种非参数的假设检验方法,用于比较两个相关配对样本的中位数是否存在差异。
该检验不依赖于数据的分布情况,适用于非正态分布的数据。
举例来说,某研究人员想要评估某种治疗方法对患者疼痛程度的影响。
该研究人员收集了30位患者的治疗前后的疼痛分数数据。
他们想知道,是否存在治疗前后的疼痛分数差异。
于是,他们可以使用Wilcoxon符号秩检验来判断。
在Wilcoxon符号秩检验中,我们的零假设(H0)是两组样本的中位数没有差异,而备择假设(H1)则是两组样本的中位数存在差异。
通过对样本数据进行计算,得到检验统计量的值,进而得到相应的p 值。
若p值小于给定的显著性水平(通常为0.05),则我们可以拒绝零假设,认为两组样本的中位数存在显著差异。
二、Mann-Whitney U检验Mann-Whitney U检验,又称为Wilcoxon秩和检验,是一种非参数的假设检验方法,用于比较两组独立样本的总体中位数是否存在差异。
该检验同样不依赖于数据的分布情况。
假设某研究人员想要比较两种不同的药物对患者血压的影响。
他们随机选择了一组患者,将他们分为两组,分别给予不同药物的治疗。
然后,他们测量了两组患者的血压数据,以了解是否存在差异。
在这种情况下,研究人员可以使用Mann-Whitney U检验进行分析。
在Mann-Whitney U检验中,我们的零假设(H0)是两组样本的中位数没有差异,而备择假设(H1)则是两组样本的中位数存在差异。

《非参数统计》试卷注意事项:1.本试卷适用于经济统计专业学生使用。
2.本试卷共6 页,满分100分,答题时间120分钟。
题号一二三四总分得分一、选择题(本大题共10小题,每小题1分,共10分)评卷人1、以下对非参数检验的描述,哪一项是错误的()。
A.非参数检验方法不依赖于总体的分布类型B.应用非参数检验时不考虑被研究对象的分布类型C.非参数检验的假定条件比较宽松D.非参数检验比较简便2、秩和检验又叫做()A、参数检验B、Wilcoxon检验C、非参数检验D、近似正态检验3、()同分校正后,统计量会变小。
A. Kruskal-Wallis检验B.弗里德曼(Friedman)检验C. Mann-Whitney检验D. Spearman等级相关检验4、配对比较的秩和检验的基本意思是:如果检验假设成立,则对样本来说()。
A.正秩和的绝对值小于负秩和的绝对值B.正秩和的绝对值大于负秩和的绝对值C.正秩和的绝对值与负秩和的绝对值不会相差很大D.正秩和的绝对值与负秩和的绝对值相等5、成组设计多个样本比较的秩和检验,当组数大于3时,统计量H近似()分布A、正态B、2C、FD、二项6、Wilcoxon符号秩检验不适用于()。
A 位置的检验B 连续总体C 随机性的检验D 配对样本的检验7、成组设计两样本比较的秩和检验中,描述不正确的是()。
A.遇有相同数据,若在同一组,取平均秩次B.遇有相同数据,若在同一组,按顺序编秩C.遇有相同数据,若不在同一组,按顺序编秩D.遇有相同数据,若不在同一组,取其秩次平均值8、m=4,n=7,Tx=14的双侧检验,则()A. Ty=41,在显著性水平0.05时接受原假设B. Ty=41,在显著性水平0.05时拒绝原假设C. Ty=42,在显著性水平0.05时拒绝原假设D. Ty=42,在显著性水平0.05时接受原假设9、序列3 5 2 7 9 8 6的一致对数目为()。
A.14B.15C.16D.1310、X的秩为1 2 3.5 3.5 5 Y相应的秩为2.5 1 2.5 5 4,则V、U分别为()。
1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
课后习题参考答案第一章p23-252、(2)有两组学生,第一组八名学生的成绩分别为x 1:100,99,99,100,99,100,99,99;第二组三名学生的成绩分别为x 2:75,87,60。
我们对这两组数据作同样水平a=0.05的t检验(假设总体均值为u ):H 0:u=100 H 1:u<100。
第一组数据的检验结果为:df=7,t 值为3.4157,单边p 值为0.0056,结论为“拒绝H 0:u=100。
”(注意:该组均值为99.3750);第二组数据的检验结果为:df=2,t 值为3.3290,单边p值为0.0398;结论为“接受H 0:u=100。
”(注意:该组均值为74.000)。
你认为该问题的结论合理吗?说出你的理由,并提出该如何解决这一类问题。
答:这个结论不合理(6分)。
因为,第一组数据的结论是由于p-值太小拒绝零假设,这时可能犯第一类错误的概率较小,且我们容易把握;而第二组数据虽不能拒绝零假设,但要做出“在水平a时,接受零假设”的说法时,还必须涉及到犯第二类错误的概率。
(4分)然而,在实践中,犯第二类错误的概率多不易得到,这时说接受零假设就容易产生误导。
实际上不能拒绝零假设的原因很多,可能是证据不足(样本数据太少),也可能是检验效率低,换一个更有效的检验之后就可以拒绝了,当然也可能是零假设本身就是对的。
本题第二组数据明显是由于证据不足,所以解决的方法只有增大样本容量。
(4分)第三章p68-713、在某保险种类中,一次关于1998年的索赔数额(单位:元)的随机抽样为(按升幂排列): 4632,4728,5052,5064,5484,6972,7596,9480,14760,15012,18720,21240,22836,52788,67200。
已知1997年的索赔数额的中位数为5064元。
(1)是否1998年索赔的中位数比前一年有所变化?能否用单边检验来回答这个问题?(4分) (2)利用符号检验来回答(1)的问题(利用精确的和正态近似两种方法)。
(10分) (3)找出基于符号检验的95%的中位数的置信区间。
(8分)解:(1)1998年的索赔数额的中位数为9480元比1997年索赔数额的中位数5064元是有变化,但这只是从中位数的点估计值看。
如果要从普遍意义上比较1998年与1997年的索赔数额是否有显著变化,还得进行假设检验,而且这个问题不能用单边检验来回答。
(4分)(2)符号检验(5分)设假设组:H 0:M =M 0=5064H 1:M ≠M 0=5064符号检验:因为n +=11,n-=3,所以k=min(n+,n-)=3精确检验:二项分布b(14,0.5),∑=-=30287.0)2/1,14(n b ,双边p-值为0.0576,大于a=0.05,所以在a水平下,样本数据还不足以拒绝零假设;但假若a=0.1,则样本数据可拒绝零假设。
查二项分布表得a=0.05的临界值为(3,11),同样不足以拒绝零假设。
正态近似:(5分)np=14/2=7,npq=14/4=3.5z=(3+0.5-7)/5.3≈-1.87>Z a/2=-1.96仍是在a=0.05的水平上无法拒绝零假设。
说明两年的中位数变化不大。
(3)中位数95%的置信区间:(5064,21240)(8分)7、一个监听装置收到如下的信号:0,1,0,1,1,1,0,0,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,0,1,0,0,1,1,1,0,1,0,1,0,1,0,0,0,0,0,0,0,0,1,0,1,1,0,0,1,1,1,0,1,0,1,0,0,0,1,0,0,1,0,1,0,1,0,0,0,0,0,0,0,0。
能否说该信号是纯粹随机干扰?(10分)解:建立假设组: H 0:信号是纯粹的随机干扰H 1:信号不是纯粹的随机干扰(2分)游程检验:因为n 1=42,n 2=34,r=37。
(2分)根据正态近似公式得:U=33.18)13442()3442()344234422(3442258.3813442344222≈-++--⨯⨯⨯⨯=≈++⨯⨯σ (2分)086.033.1858.3837-≈-=Z (2分)取显著性水平a=0.05,则Za/2=-1.96,故接受零假设,可以认为信号是纯粹的随机干扰的。
(2分)第四章p91-941、在研究计算器是否影响学生手算能力的实验中,13个没有计算器的学生(A组)和10个拥有计算器的学生(B组)对一些计算题进行了手算测试.这两组学生得到正确答案的时间(分钟)分别如下:A组:28, 20,20,27,3,29,25,19,16,24,29,16,29 B组:40,31, 25,29,30,25,16,30,39,25能否说A组学生比B组学生算得更快?利用所学的检验来得出你的结论.(12分)解、利用Wilcoxon 两个独立样本的秩和检验或Mann-Whitney U 检验法进行检验。
建立假设组:H 0:两组学生的快慢一致;H 1:A 组学生比B 组学生算得快。
(2分) 两组数据混合排序(在B 组数据下划线):3,16,16,16,19,20,20,24,25,25,25,25,27,28,29, 29, 29, 29,30, 30,31,39,40(2分)A 组秩和R A =1+3*2+5+6.5*2+8+10.5+13+14+16.5*3=120;B 组秩和R B =3+10.5*3+16.5+19.5*2+21+22+23=156(2分) A 组逆转数和U A =120-(13*14)/2=29B 组逆转数和U B =156-(10*11)/2=101(2分)当n A =13,n B =10时,样本量较大,超出了附表的范围,不能查表得Mann-Whitney 秩和检验的临界值,所以用正态近似。
计算2326.21245.16362603612/)11013(*10*132/10*132912/)1(2/-≈-≈-=++-=++-=B A B A B A A n n n n n n U Z (2分)当显著性水平a 取0.05时,正态分布的临界值Z a/2=-1.96(1分) 由于Z<Z a/2,所以拒绝H 0,说明A 组学生比B 组学生算得快。
(1分)4、在比较两种工艺(A和B)所生产的产品性能时,利用超负荷破坏性实验。
记下损坏前延迟的时间名次(数目越大越耐久)如下:方法:A B B A B A B A A B A A A B A B A A A A 序: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20用Mann-Whitney 秩和检验判断A工艺是否比B工艺在提高耐用性方面更优良?(10分)解、设假设组:H 0:两种工艺在提高耐用性方面的优良性一致;H 1:A 工艺比B 工艺更优良(1分,假设也可用符号表达式)根据样本数据知n A =13;n B =7(1分),计算A 工艺的秩和R A =1+4+6+8+9+11+12+13+15+17+18+19+20=153;(1分)B 工艺的秩和R B =2+3+5+7+10+14+16=57(1分)A 工艺的Mann-Whitney 秩和U A =R A -n A (n A +1)/2=153-(13*14)/2=62(1分)B 工艺的Mann-Whitney 秩和U B =R B -n B (n B +1)/2=57-(7*8)/2=29(1分)当n A =13,n B =7时,样本量较大,超出了附表的范围,不能查表得Mann-Whitney 秩和检验的临界值,所以用正态近似。
计算3075.16194.125.1625.1595.1612/)1713(*7*132/7*136212/)1(2/≈≈=++-=++-=B A B A B A A n n n n n n U Z (2分)当显著性水平a 取0.05时,正态分布的临界值Z a/2=1.96(1分)由于Z<Z a/2,所以样本数据提供的信息不足以拒绝H 0,可以说A 、B 两种工艺在提高耐用性方面的优良性一致,A 工艺并不比B 工艺更优良。
(1分)第五章p118-1211、对5种含有不同百分比棉花的纤维分别做8次抗拉强度试验,试验结果如表4所示(单位:g/cm 2):试问不同百分比纤维的棉花其平均抗拉强度是否一样,利用Kruskall —Wallis 检验法。
(14分) 解:建立假设组:H 0:不同百分比纤维的棉花其平均抗拉强度一样; H 1:不同百分比纤维的棉花其平均抗拉强度不一样。
(2分)已知,k=5,n 1= n 2= n 3= n 4= n 5=8(2分)。
混合排序后各观察值的秩如表4所示:由于自由度k-1=5-1=4,n j =8>5,是大样本,所以根据水平a=0.05,查X2分布表得临界值C=9.488,(2分)因为Q>C ,故以5%的显著水平拒绝H 0假设,不同百分比纤维的棉花其平均抗拉强度不一样。
(2分)7解:建立假设组:H 0:顾客对3种服务的态度无显著性差异;H 1:顾客对3种服务的态度有显著性差异。
(2分)本例中,k=3,n=15。
(2分)又因(5分)自由度k-1=3-1=2,(2分)取显著性水平a=0.05,查X2分布表得临界值c=5.992,(2分)因为Q>C ,故以5%的显著水平拒绝H 0假设,即顾客对3种服务的态度有显著性差异。
(2分)8、调查20个村民对3个候选人的评价,答案只有“同意”或“不同意”两种,结果见表1:试检验村民对这三个候选人的评价有没有区别?解:建立假设组: H 0:三个候选人在村民眼中没有区别H 1:三个候选人在村民眼中有差别(2分)6154.1843233323257)13(3431414257464169281323222222=-⨯⎭⎬⎫⎩⎨⎧--=∴=++++==++=++===∑∑∑∑θ j i j i y X y x 6857.2841385.715.2535.2501665.78414012)1(3)1(122222212≈⨯-++++⨯⨯=+-+=∴∑=N n R N N H k j jj数据适合用Cochran Q 检验(2分)。
而且已知n=20,k=3,∑x i =∑y j =28。
(2分) 计算结果见表3:表3根据表2计算得:48221266118922222222=+++==++=∑∑ j i y x (2分)则7778.048283)328266)(13(3)()[1(2222≈-⨯--=---=∑∑∑∑jj i i y y k kx x k k Q (2分) 取显著性水平a=0.05,查卡方分布表得卡方临界值C =5.9915,由于Q<C ,故无法拒绝零假设,可以认为三个候选人在村民眼中没有区别。