统计学 典型相关分析

摘要典型相关分析是多元统计分析的一个重要研究课题.它是研究两组变量之间相关的一种统计分析方法，能够有效地揭示两组变量之间的相互线性依赖关系.它借助主成分分析降维的思想，用少数几对综合变量来反映两组变量间的线性相关性质.目前它已经在众多领域的相关分析和预测分析中得到广泛应用.本文首先描述了典型相关分析的统计思想，定义了总体典型相关变量及典型相关系数，并简要概述了它们的求解思路，然后深入对样本典型相关分析的几种算法做了比较全面的论述.根据典型相关分析的推理，归纳总结了它的一些重要性质并给出了证明，接着推导了典型相关系数的显著性检验.最后通过理论与实例分析两个层面论证了典型相关分析的应用于实际生活中的可行性与优越性.【关键词】典型相关分析，样本典型相关，性质，实际应用ABSTRACTThe Canonical Correlation Analysis is an important studying topicof the Multivariate Statistical Analysis. It is the statistical analysis method which studies the correlation between two sets of variables. It can work to reveal the mutual line dependence relation availably between two sets of variables. With the help of the thought about the Principal Components, we can use a few comprehensive variables to reflect the linear relationship between two sets of variables. Nowadays It has already been used widely in the correlation analysis and forecasted analysis.This text describes the statistical thought of the Canonical Correlation Analysis firstly, and then defines the total canonical correlation variables and canonical correlation coefficient, and sum uptheir solution method briefly. After it I go deep into discuss some algorithm of the sample canonical correlation analysis thoroughly. According to the reasoning of the Canonical Correlation Analysis, sum up some of its important properties and give the identification, following it, I infer the significance testing about the canonical correlation coefficient. According to the analysis from the theories and the application, we can achieve the possibility and the superiority from canonical correlation analysis in the real life.【Key words】Canonical Correlation Analysis，Sample canonical correlation，Character，Practical applications目录前言 1第1章典型相关分析的数学描述 2第2章典型变量与典型相关系数 32.1 总体典型相关 32.2 样本典型相关 42.2.1 第一对典型相关变量的解法 42.2.2 典型相关变量的一般解法 92.2.3 从相关矩阵出发计算典型相关 9第3章典型相关变量的性质 12第4章典型相关系数的显著性检验 16第5章典型相关分析的计算步骤及应用实例 195.1 典型相关分析的计算步骤 195.2 实例分析 20结语 27致谢 28参考文献 29附录 29前言典型相关分析(Canonical Correlation Analysis ,CCA)作为多元统计学的一个重要部分，是相关分析研究的一个主要内容.典型相关分析不仅其方法本身具有重要的理论意义，而且它还可以作为其他分析方法，如多重回归、判别分析和相应分析的工具，因此在多元分析方法中占有特殊的地位.典型相关的概念是在两个变量相关的基础上发展起来的.我们知道，两个随机变量的相关关系可以用它们的简单相关系数来衡量；一个随机变量与一组随机变量之间的相关关系可以用复相关系数来衡量.但考虑一组随机变量与另一组随机变量的关系时，如果运用两个变量的相关关系，分别考虑第一组每个变量和第二组中每个变量的相关，或者运用复相关关系，考虑一组变量中的每个变量和另一组变量的相关，这样做比较繁琐，抓不住要领.因此，为了用比较少的变量来反映两组变量之间的相关关系，一种考虑的思路就是类似主成分分析，考虑两组变量的线性组合，从这两个线性组合中找出最相关的综合变量，通过少数几个综合变量来反映两组变量的相关性质，这样便引出了典型相关分析.典型相关分析的基本思想是首先在每组变量中找出变量的线性组合，使其具有最大相关性，然后再在每组变量中找出第二对线性组合，使其分别与第一对线性组合不相关，而第二对本身具有最大的相关性，如此继续下去，直到两组变量之间的相关性被提取完毕为止.有了这样线性组合的最大相关，则讨论两组变量之间的相关，就转化为只研究这些线性组合的最大相关，从而减少研究变量的个数.典型相关分析是由Hotelling于1936年提出的.就目前而言，它的理论己经比较完善，计算机的发展解决了典型相关分析在应用中计算方面的困难，成为普遍应用的进行两组变量之间相关性分析技术.如在生态环境方面，用典型相关理论对预报场与因子场进行分析，实现了短期气象预测；借助典型相关，分析了植被与环境的关系；在社会生活领域，应用典型相关分析了物价指标和影响物价因素的相关关系等等.第1章典型相关分析的数学描述一般地，假设有一组变量与另一组变量，我们要研究这两组变量之间的相关关系，如何给两组变量之间的相关性以数量的描述.当1时，就是我们常见的研究两个变量与之间的简单相关关系，其相关系数是最常见的度量，定义为：当（或）时，维随机向量，设，，其中，是第一组变量的协方差阵，是第一组与第二组变量的协方差阵，是第二组变量的协方差阵.则称为与的全相关系数，全相关系数用于度量一个随机变量与另一组随机变量的相关系数.当时，利用主成分分析的思想，可以把多个变量与多个变量之间的相关化为两个新的综合变量之间的相关.也就是做两组变量的线性组合即其中，和为任意非零向量，于是我们把研究两组变量之间的问题化为研究两个变量之间的相关问题，希望寻求，使，之间最大可能的相关，我们称这种相关为典型相关，基于这种原则的分析方法就是典型相关分析.第2章典型变量与典型相关系数2.1 总体典型相关设有两组随机变量,,分别为随机向量，根据典型相关分析的思想，我们用和的线性组合和之间的相关性来研究两组随机变量和之间的相关性.我们希望找到，使得最大.由相关系数的定义易得出对任意常数，均有这说明使得相关系数最大的并不唯一.因此，为避免不必要的结果重复，我们在求综合变量时常常限定，于是，我们就有了下面的定义：设有两组随机变量，，维随机向量的均值向量为零，协方差阵（不妨设）.如果存在和，使得在约束条件，下，则称是的典型相关变量，它们之间的相关系数称为典型相关系数；其他典型相关变量定义如下：定义了前对典型相关变量之后，第对典型相关变量定义为：如果存在和，使得⑴和前面的对典型相关变量都不相关；⑵，；⑶的相关系数最大，则称是的第对（组）典型相关变量，它们之间的相关系数称为第个典型相关系数（）.2.2 样本典型相关以上是根据总体情况已知的情形进行，而实际研究中，总体均值向量和协方差阵通常是未知的，因而无法求得总体的典型相关变量和典型相关系数，首先需要根据观测到的样本数据阵对进行估计.2.2.1 第一对典型相关变量的解法设总体，已知总体的次观测数据为：（），于是样本数据阵为若假定则由参考文献【2】中定理2.5.1知协方差阵的最大似然估计为其中=，样本协方差矩阵为：。

统计学中常用的数据分析方法
典型相关分析
相关分析一般分析两个变量之间的关系，而典型相关分析是分析两组变量（如3个学术能力指标与5个在校成绩表现指标）之间相关性的一种统计分析方法。

典型相关分析的基本思想和主成分分析的基本思想相似，它将一组变量与另一组变量之间单变量的多重线性相关性研究转化为对少数几对综合变量之间的简单线性相关性的研究，并且这少数几对变量所包含的线性相关性的信息几乎覆盖了原变量组所包含的全部相应信息。

R0C分析
R0C曲线是根据一系列不同的二分类方式(分界值或决定阈）.以真阳性率（灵敏度)为纵坐标，假阳性率（1-特异度)为横坐标绘制的曲线
用途：
1、R0C曲线能很容易地査出任意界限值时的对疾病的识别能力用途；
2、选择最佳的诊断界限值。

R0C曲线越靠近左上角，试验的准确性就越高；
3、两种或两种以上不同诊断试验对疾病识别能力的比较，一股用R0C曲线下面积反映诊断系统的准确性。

统计学专业基础课与专业课之间的典型相关分析摘要本文基于统计学系0301－0302两个班的66名学生17门课程（包括专业基础课和专业课）的考试成绩，运用典型相关分析法研究了统计学系基础课和专业课的相关程度。

通过运用统计分析软件SAS运行得到变量间的相关系数以及标准化后的典型相关系数，进而求出典型相关变量。

最后结合分析结果和实际情况对教学提了一点小小的建议。

关键词：基础课；专业课；典型相关分析；典型相关系数Canonical Correlation Analysis Between The Major and BasicSubjects of The Statistics MajorAbstractWith the method of canonical correlation analysis,I study about the correlation between the major and basic subjects of the statistics major.The research is based on the examination scores of66students of classes0301and0302who are in the major of statistics,including only17 subjects,the major and basic subjects.The article then gives the standard canonical correlations between the variables from which we can know the canonical correlative variables.In the end,I give some suggestions about education,according to the output of the analysis and the matter of fact.Key word:basic subject,major,canonical correlation,canonical coefficients1引言对于统计学系的学生来说，对数学理论的理解和掌握要求比较高，而且更重要的是要做到融会贯通，举一反三，学会理论联系实际，并利用统计分析的方法来解决日常生产生活中的问题，因而专业基础课程（如数学分析和高等代数等）的学习无疑是相当重要的，因为它直接关系到后续专业课的学习效果。

统计学中的相关分析方法统计学是一门研究数据收集、整理、分析和解释的学科，是现代科学研究中不可或缺的一部分。

在统计学中，相关分析是一种重要的方法，用于研究变量之间的关系。

本文将介绍相关分析的基本概念、方法和应用。

一、相关分析的基本概念相关分析是一种用来研究两个或多个变量之间关系的统计方法。

它通过计算相关系数来衡量变量之间的相关性。

相关系数是一个介于-1和1之间的数值，表示变量之间的相关程度。

当相关系数接近1时，表示变量之间存在强正相关；当相关系数接近-1时，表示变量之间存在强负相关；当相关系数接近0时，表示变量之间不存在线性相关。

二、相关分析的方法相关分析有多种方法，其中最常用的是皮尔逊相关系数。

皮尔逊相关系数是一种度量变量之间线性相关程度的方法。

它可以用来研究两个变量之间的关系，也可以用来研究多个变量之间的关系。

皮尔逊相关系数的计算公式如下：r = (Σ(Xi - X)(Yi - Ȳ)) / √(Σ(Xi - X)²Σ(Yi - Ȳ)²)其中，r表示相关系数，Xi和Yi分别表示第i个观测值的两个变量的取值，X和Ȳ分别表示两个变量的平均值。

除了皮尔逊相关系数，还有一些其他的相关分析方法，例如斯皮尔曼相关系数、切比雪夫距离等。

这些方法适用于不同类型的数据和不同的研究问题，研究者可以根据具体情况选择合适的方法进行分析。

三、相关分析的应用相关分析在各个领域都有广泛的应用。

在经济学中，相关分析可以用来研究经济变量之间的关系，例如GDP和失业率之间的关系、股票价格和利润之间的关系等。

在医学研究中，相关分析可以用来研究疾病和生活方式之间的关系，例如吸烟和肺癌之间的关系、饮食和心脏病之间的关系等。

在市场营销中，相关分析可以用来研究产品销量和广告投放之间的关系，帮助企业制定营销策略。

除了上述应用，相关分析还可以用来研究教育、环境、社会等领域的问题。

例如，在教育研究中，可以用相关分析来研究学生的学习成绩和学习时间之间的关系；在环境研究中，可以用相关分析来研究气候变化和自然灾害之间的关系；在社会研究中，可以用相关分析来研究收入和幸福感之间的关系。

统计学中的相关分析统计学是一门研究数据收集、分析和解释的学科，而相关分析是其中一个重要的分析方法。

相关分析是用来量化两个或更多变量之间关系强度的技术，它可以帮助我们理解和预测现象之间的相关性。

本文将介绍相关分析的基本概念、应用以及在实际问题中的运用。

一、相关分析的概念相关分析是统计学中用来确定两个或多个变量之间关系强度的方法。

关系强度通过相关系数来度量，相关系数的取值范围为-1到1。

相关系数为正值表示两个变量是正相关的，即随着一个变量的增加，另一个变量也会增加；相关系数为负值表示两个变量是负相关的，即随着一个变量的增加，另一个变量会减少；相关系数为零表示两个变量之间没有线性关系。

相关分析可以帮助我们了解变量之间的关系，并进行进一步的预测和分析。

二、相关分析的应用相关分析在实际问题中有着广泛的应用。

以下是几个常见领域的相关分析应用示例：1. 经济学领域：相关分析可以帮助经济学家确定不同经济指标之间的关系，如通货膨胀率与失业率之间的相关性，利率与投资之间的相关性等。

这些关系可以用来预测经济发展趋势，为经济政策制定提供参考依据。

2. 医学研究：相关分析在医学研究中的应用非常广泛。

例如，研究人员可以使用相关分析来确定吸烟与肺癌之间的关系，体重与心血管疾病之间的关系等。

这些关系可以帮助医生们更好地了解疾病的发展机制，并提供有效的预防和治疗方案。

3. 市场调查：相关分析可以用来确定市场调查数据中不同变量之间的关系。

例如，一家公司可以使用相关分析来确定广告投资与销售额之间的关系，从而确定最佳的广告投放策略。

相关分析还可以帮助市场调查人员找到潜在的目标客户群体，以提升市场营销效果。

三、相关分析的实际案例为了更好地理解相关分析的应用，我们将通过一个实际案例来说明其具体操作。

假设一个电商公司想要研究用户购买行为与广告点击率之间的关系。

他们分析了一段时间内的用户购买记录和广告点击数据，并进行了相关分析。

他们计算了购买金额和广告点击率之间的相关系数，并得到了一个正值0.75。

统计学相关分析统计学是一门研究数据收集、分析与解释的学科。

它的目标是通过系统和科学的方法研究数据，以便能够对各种现象进行描述、理解和预测。

统计学的应用非常广泛，涵盖了自然科学、社会科学、医学、工程、经济学等各个领域。

其中，相关分析是统计学的一个重要工具，可以用来研究两个或多个变量之间的关系。

相关分析是指研究两个或多个变量之间的关系的统计方法。

它可以用来确定这些变量之间是否存在其中一种关联性，并且可以量化这种关联性的强度和方向。

相关分析中常用的指标是相关系数，它可以衡量两个变量之间的线性关系。

相关系数是一个介于-1到+1之间的数值，它表示着两个变量之间的关联程度。

如果相关系数为-1，表示两个变量呈现完全负相关，即一个变量的增加导致另一个变量的减少；如果相关系数为+1，表示两个变量呈现完全正相关，即一个变量的增加导致另一个变量的增加；如果相关系数为0，表示两个变量之间没有线性关系。

相关分析有很多应用，尤其在社会科学和市场研究领域。

例如，在经济学中，相关分析可以用来研究不同经济指标之间的关系，进而预测经济发展的趋势。

在市场研究中，相关分析可以用来研究产品销售量与广告投入之间的关系，从而为企业制定营销策略提供支持。

在医学研究中，相关分析可以用来研究药物治疗效果与患者病情之间的关系，以便优化治疗方案。

进行相关分析的步骤通常包括以下几个方面：1.收集数据：首先需要收集两个或多个变量的相关数据。

这些数据可以通过实验、调查或观察来获取。

2.计算相关系数：根据收集到的数据，可以使用相关系数来度量变量之间的关系。

最常用的是皮尔逊相关系数，它适用于连续性变量。

如果变量是分类变量，可以使用斯皮尔曼相关系数。

3.判断关联性：计算出相关系数之后，就可以判断变量之间的关联性。

一般来说，绝对值大于0.7的相关系数被视为强相关，绝对值在0.3到0.7之间的相关系数被视为中等相关，而绝对值小于0.3的相关系数被视为弱相关。

4.分析结果：根据相关系数的大小和方向，可以对变量之间的关系进行解释。

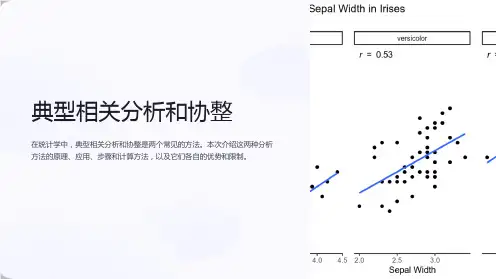
多元统计分析——典型相关分析典型相关分析（Canonical correlation analysis）是一种多元统计分析方法，用于研究两组变量之间的关联性。

与传统的相关分析不同，典型相关分析可以同时考虑多组变量，找出最佳的线性组合，使得两组变量之间的相关性最大化。

它主要用于探索一组自变量与另一组因变量之间的线性关系，并且可以提供详细的相关性系数、特征向量和特征值等信息。

典型相关分析的基本原理是将两组变量分别投影到最佳的线性组合上，使得投影后的变量之间的相关性最大。

这种投影是通过求解特征值问题来实现的，其中特征值表示相关系数的大小，特征向量表示两组变量的线性组合。

通常情况下，我们希望保留具有最大特征值的特征向量，因为它们对应着最强的相关性。

典型相关分析的应用广泛，可以用于众多领域，如心理学、社会科学、经济学等。

例如，在心理学研究中，我们可能对人们的人格特征和行为方式进行测量，然后使用典型相关分析来探索它们之间的关系。

在经济学研究中，我们可以将宏观经济指标与企业盈利能力进行比较，以评估它们之间的相关性。

典型相关分析的步骤如下：1.收集数据：首先，我们需要收集两组变量的数据。

这些数据可以是定量数据（如收入、年龄）或定性数据（如性别、职业）。

2.建立模型：然后，我们需要建立一个数学模型，用于描述两组变量之间的关系。

这可以通过线性回归、主成分分析等方法来实现。

3.求解特征值问题：接下来，我们需要求解特征值问题，以获得相关系数和特征向量。

在实际计算中，我们可以使用统计软件来完成这一步骤。

4.解释结果：最后，我们需要解释典型相关分析的结果。

通常情况下，我们会关注最大的特征值和对应的特征向量，因为它们表示着最强的相关性。

典型相关分析的结果提供了一组线性组合，这些组合可以最大化两组变量之间的相关性。

通过分析这些组合，我们可以洞察两组变量之间的潜在关系，并提供有关如何解释和预测这种关系的指导。

总结而言，典型相关分析是一种强大的多元统计分析方法，可以用于研究两组变量之间的关联性。

统计数据的相关性分析统计数据的相关性分析是一种用来研究两个或多个变量之间关系的方法。

通过分析变量之间的相关性，可以得出它们之间的关联程度，并帮助我们理解它们之间的相互作用。

在实际应用中，统计数据的相关性分析广泛应用于经济学、社会学、医学、市场研究等领域，能够帮助我们做出科学决策和预测。

一、相关性的定义和计算方法相关性是指两个变量之间的关联程度。

在统计学中，通过计算相关系数来衡量变量之间的相关性。

最常用的相关系数是皮尔逊相关系数，用来衡量两个连续变量之间的线性关系。

皮尔逊相关系数的取值范围为-1到1，其中1表示完全正相关，-1表示完全负相关，0表示无相关性。

计算皮尔逊相关系数的公式如下所示：r = (Σ(Xi - X)(Yi - Ȳ)) / √((Σ(Xi - X)²)(Σ(Yi - Ȳ)²))其中，Xi和Yi分别表示两个变量的取值，X和Ȳ分别表示两个变量的平均值。

二、相关性分析的步骤进行相关性分析通常需要经历以下步骤：1.数据准备：首先，收集和整理需要分析的数据。

确保数据完整、准确，并做必要的数据清洗。

如果数据中存在缺失值或异常值，需要进行处理。

2.计算相关系数：使用合适的统计软件或编程语言，计算变量之间的相关系数。

可以使用皮尔逊相关系数、斯皮尔曼相关系数等。

3.解读相关系数：根据计算得到的相关系数，进行解读。

一般来说，当相关系数接近1或-1时，表示变量之间存在强相关性；当相关系数接近0时，表示变量之间不存在相关性。

4.绘制图表：通过绘制散点图或其他相关图表，可以更直观地展示变量之间的关系。

可以使用统计软件或数据可视化工具进行绘制。

5.验证结果：如果相关系数表明变量之间存在相关性，可以进行一些统计验证，例如假设检验等，以确保结果的可靠性和统计显著性。

三、相关性分析的应用相关性分析在实际应用中具有广泛的应用价值，以下是一些常见的应用场景：1.经济学：相关性分析可以用于探索经济指标之间的关系，例如GDP和失业率之间的关系，通货膨胀率和利率之间的关系等。

统计学中的相关分析与回归分析统计学中的相关分析与回归分析是两种重要的数据分析方法。

它们帮助研究人员理解和解释变量之间的关系，并预测未来的趋势。

在本文中，我们将深入探讨相关分析和回归分析的定义、应用和原理。

第一部分：相关分析相关分析是用来衡量和评估两个或更多变量之间相互关系的统计方法。

通过相关系数来量化这种关系的强度和方向。

相关系数的取值范围在-1到+1之间，其中-1表示完全负相关，+1表示完全正相关，0表示没有相关性。

相关分析通常用于发现变量之间的线性关系。

例如，研究人员想要了解身高和体重之间的关系。

通过相关分析，他们可以确定是否存在正相关关系，即身高越高，体重越重。

相关分析还可以帮助确定不同变量对某一结果变量的影响程度。

第二部分：回归分析回归分析是一种通过建立数学模型来预测和解释变量之间关系的方法。

它可以用来预测因变量的值，并了解自变量对因变量的影响程度。

回归分析可分为简单回归和多元回归两种类型。

简单回归分析适用于只有一个自变量和一个因变量的情况。

例如，研究人员想要预测一个人的体重，他们可以使用身高作为自变量。

通过建立线性回归模型，他们可以得到身高对体重的影响，从而预测一个人的体重。

多元回归分析适用于有多个自变量和一个因变量的情况。

例如，研究人员想要了解影响一个城市房价的因素，他们可以考虑多个自变量，如房屋面积、地理位置、房龄等。

通过建立多元回归模型，他们可以确定每个因素对房价的影响程度，并进行预测。

第三部分：相关分析与回归分析的应用相关分析和回归分析在各个领域都有广泛的应用。

在医学研究中，相关分析可以帮助确定两个疾病之间的关联性，并为疾病的预防和治疗提供依据。

回归分析可以用来预测患者的生存率或疾病的发展趋势。

在经济学中，相关分析可以用来研究经济变量之间的关系，如GDP 与通货膨胀率之间的关系。

回归分析可以用来预测经济增长率，并评估政治和经济因素对经济发展的影响。

在市场营销中，相关分析可以帮助企业了解产品销售和广告投放之间的关系，并制定有效的市场推广策略。

典型相关分析典型相关分析是一种统计学方法，用于研究两组变量之间的关系。

典型相关分析可以帮助我们了解这两组变量之间的相互关系以及它们是否能够彼此预测。

在本文中，我们将探讨典型相关分析的基本概念、应用场景、计算方法以及结果的解释和解读。

典型相关分析，又称为典型相关系数分析，是一种多变量统计技术，它可以在两组变量之间寻找最具相关性的线性组合，这个线性组合被称为典型变量。

典型相关分析的核心思想是将两组变量转化为一组最具相关性的综合变量，以便探索和解释它们之间的关系。

典型相关分析通常用于探索两组变量之间的关系，并确定是否存在一个或多个典型相关系数。

在许多实际应用中，这些变量可能代表相互关联的特征或维度，比如市场规模和销售额、学习时间和考试成绩等。

典型相关分析可以用于许多领域的研究。

例如，在市场研究中，我们可以使用典型相关分析来研究不同市场因素之间的关系，并确定市场的发展趋势。

在教育研究中，我们可以使用典型相关分析来研究学生的学习习惯和学术成绩之间的关系，以帮助教育者改进教学方法和学习环境。

接下来，我们将介绍典型相关分析的计算方法。

假设我们有两组变量X和Y，其中X包含p个变量，Y包含q个变量。

首先，我们计算X和Y的样本协方差矩阵SXX和SYY，以及它们之间的协方差矩阵SXY。

然后，我们对SXX和SYY进行特征值分解，得到它们的特征向量和特征值。

接下来，我们选择最大的r个特征值和对应的特征向量。

最后，我们计算典型相关系数以及典型变量。

结果的解释和解读是典型相关分析的最后一步。

典型相关系数的取值范围为-1到1，其中取值为1表示两组变量之间存在完全正相关的关系，取值为-1表示存在完全负相关的关系，取值为0表示两组变量之间不存在相关性。

此外，我们还可以通过检验统计量来判断典型相关系数是否显著。

总结起来，典型相关分析是一种统计学方法，用于研究两组变量之间的关系。

它可以帮助我们了解这两组变量之间的相互关系以及它们是否能够彼此预测。

统计学中的相关分析方法及其实用性引言：统计学是一门研究数据收集、整理、分析和解释的学科，广泛应用于各个领域。

其中，相关分析是统计学中一种常见且实用的方法，用于研究变量之间的关系。

本文将介绍相关分析的基本概念、常见的相关系数以及其在实际应用中的实用性。

一、相关分析的基本概念相关分析是一种研究变量之间关系的统计方法。

通过相关分析，我们可以了解变量之间的相关性强弱以及相关性的方向。

相关分析可以帮助我们理解变量之间的关系，预测未来的趋势，以及为决策提供依据。

二、常见的相关系数1. 皮尔逊相关系数皮尔逊相关系数是最常见的相关系数之一，用于衡量两个连续变量之间的线性相关程度。

它的取值范围在-1到1之间，其中-1表示完全负相关，1表示完全正相关，0表示无相关。

皮尔逊相关系数的计算基于变量的协方差和标准差，可以通过公式进行计算。

2. 斯皮尔曼相关系数斯皮尔曼相关系数是一种非参数的相关系数，用于衡量两个变量之间的单调关系。

与皮尔逊相关系数不同，斯皮尔曼相关系数不要求变量呈现线性关系，而是通过对变量的排序来计算相关系数。

斯皮尔曼相关系数的取值范围也在-1到1之间，具有与皮尔逊相关系数类似的解释。

3. 切比雪夫相关系数切比雪夫相关系数是一种用于衡量两个变量之间关系的非参数方法。

它基于两个变量的差值的绝对值，而不是变量的具体数值。

切比雪夫相关系数的取值范围在0到1之间，其中0表示没有相关性，1表示完全相关。

三、相关分析的实用性相关分析在实际应用中具有广泛的实用性。

以下是几个相关分析在不同领域的实际应用示例：1. 经济学领域相关分析在经济学领域中被广泛应用，用于研究经济指标之间的关系。

例如，可以通过相关分析来研究利率和通货膨胀之间的关系，以及GDP和就业率之间的关系。

这些分析可以帮助政府和企业做出更准确的经济决策。

2. 医学研究相关分析在医学研究中也具有重要的应用价值。

例如，可以通过相关分析来研究吸烟和肺癌之间的关系，以及体重和心脏病之间的关系。

第5讲相关分析与相关系数相关分析，也被称为相关性分析，是统计学中一种用于评估两个或多个变量之间关系的方法。

通过相关分析，我们可以了解两个变量之间是否存在其中一种关联，以及关联的强度和方向。

相关系数是用来度量两个变量之间相关性的指标。

常用的相关系数有皮尔逊相关系数、斯皮尔曼相关系数和刻度相关系数。

皮尔逊相关系数是衡量两个连续变量之间线性关系强度和方向的常用指标。

它的取值范围介于-1和1之间，其中-1表示完全的负相关，0表示无相关，1表示完全的正相关。

计算皮尔逊相关系数的方法是通过两个变量的协方差除以它们的标准差的乘积。

斯皮尔曼相关系数是用于衡量两个有序变量之间相关性的指标。

它不要求变量之间服从线性关系，而是通过对两个变量的排序来计算相关系数。

斯皮尔曼相关系数的取值范围也是-1到1之间，其中-1表示完全的负相关，0表示无相关，1表示完全的正相关。

刻度相关系数（Kendall's tau）是衡量两个有序变量之间相关性的非参数指标，适用于样本量较小或变量不满足正态分布的情况。

刻度相关系数的取值范围也是-1到1之间，其中-1表示完全的负相关，0表示无相关，1表示完全的正相关。

在进行相关分析时，首先要对变量之间的关系进行可视化。

常用的方法是绘制散点图来展示变量之间的关系。

如果散点图呈现一种线性的趋势，即随着一个变量的增加，另一个变量也随之增加（或减少），那么这两个变量之间很可能存在线性相关。

如果散点图呈现一种曲线的趋势，那么这两个变量之间可能存在非线性相关。

如果散点图呈现一种随机分布的形式，那么这两个变量之间可能没有相关性。

然后使用相关系数来度量变量之间的相关性。

通过计算相关系数的值，我们可以判断变量之间的相关性强弱及方向。

但是需要注意的是，相关系数只能反映变量之间的线性关系，对于非线性关系可能无法准确度量。

相关分析在实际应用中有着广泛的应用。

例如，在市场调研中，我们可以通过相关分析来评估两个市场指标之间的关系，以及它们对销售量的影响。