导线线间距离计算

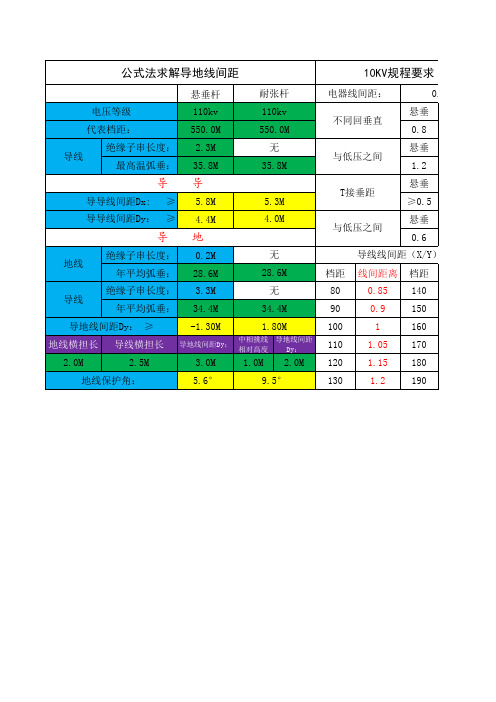
架空线路导线及地线的要求对架空线路导线及地线的要求主要有以下方面：材料要求、线间距离要求、弧垂要求、对地及交叉跨越要求、导、地线间的连接要求、导线与地线的配合要求等。

总体要求为：选择具有良好电气性能和机械性能的材料，保证安全可靠的运行参数（限距、弧垂等），采用合理的施工工艺。

一、对导、地线材料的要求：1、对导线材料的要求：导线的功能和工况一一传输电能，通电、承受机械荷载。

对其材料的基本要求为：具有良好的导电性能及足够的机械强度，并具有一定的耐腐蚀、耐高温和可加工性能，且重量轻、性能稳定，耐磨损，价格低廉等。

能满足上述要求的材料主要为铝和钢，前者导电性能好但机械强度较差；后者则导电性能差而机械性能好。

因此目前大多用这两种材料组合制作导线，如钢芯铝绞线等。

2、对地线材料的要求：架空地线的作用：引雷入地，减少雷击线路而跳闸的机会，提高线路的耐雷水平，保证线路安全送电。

架空地线的类别:普通架空地线一不与杆塔绝缘，只起引雷入地的作用；绝缘架空地线一与杆塔绝缘，起引雷入地的作用，还可作载波通讯的通道、地线自身的融冰、检修时电动电源及小功率用户的供电等对普通架空地线材料：只要求有较高的机械性能及良好的耐腐蚀性能，一般采用钢绞线。

对绝缘地线材料：较高的机械性能、良好的耐疲劳性、耐腐蚀性能及良好的导电性。

一般采用钢芯铝绞线、铝镁合金绞线和铝包铜绞线等。

以降低通讯衰减，提高通讯质量。

二、导线的线间距离要求：导线的线间距离主要指导线间的水平距离、垂直距离和水平偏移距离。

确定的依据一一保证足够的电气间隙，确保导线之间及导线与杆塔接地。

导线的线路间距离主要取决于以下情况：1)导线风偏后对杆塔的最小空气间隙应满足规程要求；2)档距中央导线之间不得发生闪络和鞭击现象。

实践证明：对110kV以上的线路：因为其绝缘子串较长，风偏角大，其线间距离一般由第一种情况控制。

对110kV以下的线路：绝缘子串较短，而档距中央弧垂最大，故以第二种情况来限制导线间的距离。

参数计算（第一版）1.线路参数计算内容已知量：线路型号(导线材料、截面积mm 2)、长度(km)、排列方式、线间距离(m)、外径(mm)、分裂数、分裂距(m)、电压等级(kV)、基准电压U B (kV, 母线电压作为基准电压)、基准容量S B (100MVA)。

待计算量：电阻R(Ω/km)、线电抗X(Ω/km)、零序电阻R0(Ω/km)、零序电抗X0(Ω/km)、对地电纳B(S/km)、对地零序电纳B0(S/km)。

计算公式： 1.3.1线路电阻R=ρ/S (Ω/km)R*=R2BBU S 式中ρ——导线材料的电阻率(Ω·mm 2/km)； S ——线路导线的额定面积（mm 2）。

1.3.2线路的电抗X=eqm r D +n 0157.0(Ω/km)X*=X 2BBU S式中m D ——几何均距,m D =ac bc ab D D D (mm 或cm,其单位应与eq r 的单位相同);eq r ——等值半径, eq r =n n m rD 1(mm,其中r 为导线半径);n ——每个导线的分裂数。

1.3.3零序电阻R0=R+3R g (Ω/km)R0*=R02BBU S 式中R g ——大地电阻, R g =π2×10-4×f =×10-4×f (Ω/km)。

在f =50Hz 时，R g =Ω/km 。

1.3.4零序电抗X0=sg D D (Ω/km)X0*=X02BBU S 式中g D ——等值深度, g D =γf 660,其中γ为土壤的电导率,S/m 。

当土壤电导率不明确时，在一般计算中可取g D =1000m 。

s D ——几何平均半径, s D =32m D r '其中r '为导线的等值半径。

若r 为单根导线的实际半径，则对非铁磁材料的圆形实心线，r '=r ;对铜或铝的绞线，r '与绞线股数有关，一般r '=~r ；纲芯铝线取r '=r ；若为分裂导线，r '应为导线的相应等值半径。

参数计算（第一版）1.线路参数计算内容1.1已知量：线路型号(导线材料、截面积mm 2)、长度(km)、排列方式、线间距离(m)、外径(mm)、分裂数、分裂距(m)、电压等级(kV)、基准电压U B (kV , 母线电压作为基准电压)、基准容量S B (100MV A)。

1.2待计算量：电阻R(Ω/km)、线电抗X(Ω/km)、零序电阻R0(Ω/km)、零序电抗X0(Ω/km)、对地电纳B(S/km)、对地零序电纳B0(S/km)。

1.3计算公式： 1.3.1线路电阻R=ρ/S (Ω/km) R*=R2BBU S 式中ρ——导线材料的电阻率(Ω·mm 2/km)； S ——线路导线的额定面积（mm 2）。

1.3.2线路的电抗X=0.1445lgeqm r D +n 0157.0(Ω/km)X*=X 2BBU S式中m D ——几何均距,m D =ac bc ab D D D (mm 或cm,其单位应与eq r 的单位相同);eq r ——等值半径, eq r =n n m rD 1(mm,其中r 为导线半径);n ——每个导线的分裂数。

1.3.3零序电阻R0=R+3R g (Ω/km)R0*=R02BBU S 式中R g ——大地电阻, R g =π2×10-4×f =9.869×10-4×f (Ω/km)。

在f =50Hz 时，R g =0.05Ω/km 。

1.3.4零序电抗X0=0.4335lgsg D D (Ω/km)X0*=X02BBU S 式中g D ——等值深度, g D =γf 660,其中γ为土壤的电导率,S/m 。

当土壤电导率不明确时，在一般计算中可取g D =1000m 。

s D ——几何平均半径, s D =32m D r '其中r '为导线的等值半径。

若r 为单根导线的实际半径，则对非铁磁材料的圆形实心线，r '=0.779r ;对铜或铝的绞线，r '与绞线股数有关，一般r '=0.724~0.771r ；纲芯铝线取r '=0.95r ；若为分裂导线，r '应为导线的相应等值半径。

架空送电线路导线电气距离的公式计算方法摘要：建立架空送电线路导线空间曲线方程的方式，运用微积分等数学理论对点与导线、直线与导线、导线与导线之间的最小电气距离的公式求解方法进行了系统推导，所得计算方法与以往工程设计中通常采用的作图法、解析法及穷举法相比．具有计算简单、结果精确、适用范围广等优点。

关键词：架空送电线路；电气距离公式；计算方法1前言在架空线路设计中，对导线电气距离的计算是一项非常重要的内容。

如导线对交叉跨越物或设备的安全距离校核、导线风偏后对危险点的电气距离校核、导线与杆塔和拉线之间的电气间隙计算、导线换相后的线间距离验算等。

以往工程设计中通常采用作图法、解析法及穷举法来进行电气距离或电气间隙的计算，这些方法不仅工作量大、精度差，而且有时需对某些参数模型作近似处理。

并且对导线与交叉跨越物、危险点、杆塔、拉线等的电气距离或电气间隙的计算需采用不同的作图方法和计算方法。

本文采取建立架空送电线路导线空间曲线方程的方式，运用微积分等数学理论对点与导线、直线与导线、导线与导线之间的最小电气距离或电气间隙的公式求解方法进行系统论述。

2导线空间曲线方程的建立首先，建立空间直角坐标系，确定X轴为横轴，Y轴为纵轴，Z轴为立轴(方向垂直地面向上)，坐标原点在以上基础上可以任意确定。

为方便起见，X轴方向可与线路方向一致。

设已知导线2悬点(或起讫点)的坐标为(x1，y1，z1)和(x2，y2，z2)，t为参数，则导线2悬点连线的空间曲线参数方程为：设已知导线水平应力为δ0，垂直比载为γ0，水平比载为γ4，则根据《电力工程高压送电线路设计手册》可知，导线任一点(x，y，z)的弧垂按斜抛物线公式为：因此有：导线在有风偏情况下的风偏角为：风偏后弧垂对导线悬点连线的空间直线Z轴方向(垂直地面方向)的变化量为:，风偏后弧垂对导线悬点连线的空间直线X、l，轴方向(水平面方向)的变化量为：。

设导线悬点连线直线与X轴在水平面上的夹角为仅，则:线风偏有向线路左侧(X轴左侧)或向线路右侧(X轴右侧)风偏的2种不同情况，当导线向线路左侧风偏时，风偏后弧垂对导线悬点连线的空间直线X轴方向的变化量为：，Y轴方向的变化量为：当导线向线路右侧风偏时。

架空送电线路导线电气距离的公式计算方法徐海博摘要：在我国架空线路设计中，对导线电气距离的计算是一项非常重要的内容．如导线对交叉跨越物或设备的安全距离校核、导线风偏后对危险点的电气距离校核、导线与杆塔和拉线之间的电气间隙计算、导线换相后的线间距离验算等。

以往工程设计中通常采用作图法、解析法及穷举法来进行电气距离或电气间隙的计算，这些方法不仅工作量大、精度差，而且有时需对某些参数模型作近似处理。

并且对导线与交叉跨越物、危险点、杆塔、拉线等的电气距离或电气间隙的计算需采用不同的作图方法和计算方法。

关键词：架空线路；导线；电气距离现在的架空送电线路设计中，对导线电气距离的公式计算是其中非常重要的一项内容，通过对架空送电线路中导线电气距离的计算过程推导，得出的计算方法相较于传统的计算方法更为准确和简单，而且这种计算方式也是现在架空送电线路中导线电气距离计算最常用的一种求解方式。

一、地脚螺栓型式初步选择以本地区实际工程某－西区110kV线路为例，计算其#50-51杆塔之间与建筑物的距离，导线采用LGJ-240/30型钢芯铝绞线，地线采用GJ-80型钢绞线和OPGW-24B1型复合光缆，（1）导地线参数。

为方便计算，地线参数均取值GJ-80型钢绞线。

（2）导地线比载计算比载，表示架空线路单位长度（1m）、单位面积（1mm2）的荷载，一档架空线路的总荷载为：G=q•L=g•A•L式中：A—架空线路的截面积；L—档架空线路的长度在计算中常用到的一般为自荷载Ｐ1（0，0），冰荷载Ｐ2（10，0）、自荷载加冰荷载Ｐ3（10，0），无冰时的风荷载Ｐ4（0，10）、无冰时的风荷载Ｐ4（0，15）、无冰时的风荷载Ｐ4（0，25）、覆冰时的风荷载Ｐ5（10，10）、无冰时综合荷载Ｐ6（0，10）、无冰时综合荷载Ｐ6（0，15）、无冰时综合荷载Ｐ6（0，25）、覆冰时综合荷载Ｐ7（10，10），括号中的两个数值分别表示冰厚b（mm）和风速（m/s）结合本工程杆塔使用情况，查看杆塔结构图得知：塔头处导地线间的水平距离Ｌs=2.45ｍ塔头处导地线间的垂直距离Ｌh=2.638ｍ绝缘子串型式：FXBW4-110/70经配合计算后，得出以下结果：由Ｓ≥0.012Ｌ+1米配合间距解得Ｌq=403.682（ｍ）张力计算过程中实际选用的档距值Ｌx=403.682（ｍ）（3）导线风偏角计算导线风偏角计算公司如下：γ=tg-1[P4（0，25）/P1（0，0）]式中：γ—导线的风偏角；P4（0，25）—无冰时的风荷载；P1（0，0）—自荷载；经计算，导线风偏角γ=40.5464。

在电气工程领域中，对于不同回路不同相导线间的最小相间距离这一主题，我们需要深入探讨其在实际工程中的重要性和影响因素。

在本文中，将从基础概念、影响因素、设计规范和实际案例等多个方面进行分析和阐述，以期能够全面、深入地理解这一主题。

一、基础概念不同回路不同相导线间的最小相间距离是指在电力系统中，不同回路间或不同相间的导线之间需要保持一定的距离，以确保电力系统的安全运行。

这一概念是基于电力系统中的绝缘和安全防护考虑而提出的。

在实际工程中，不同回路不同相导线间的最小相间距离通常由设计规范和标准来规定，并且会受到诸多因素的影响。

下面我们将逐一进行深入讨论。

二、影响因素1. 电压等级：不同的电压等级会对最小相间距离产生影响。

一般来说，电压等级越高，对安全间距的要求也就越大。

2. 环境条件：不同环境条件下，例如高温、潮湿等，也会对导线间的最小相间距离提出特殊要求，以保证系统的安全可靠运行。

3. 设备类型：不同类型的设备，例如变压器、开关设备等，其最小相间距离的要求也会不同。

......(继续探讨其他影响因素)三、设计规范根据国家标准或行业规范，不同回路不同相导线间的最小相间距离都是有明确规定的。

以我国《电气装置安装工程质量验收规范》为例，对于不同回路不同相导线间的最小相间距离提出了具体的要求，以确保电气系统的安全性和可靠性。

在设计过程中，工程师需要严格遵循规范要求，对不同回路不同相导线间的最小相间距离进行合理设置，并在实际施工中进行严格的监测和验收，以确保符合规范要求。

四、案例分析在实际工程中，不同回路不同相导线间的最小相间距离的设置对电气系统的安全运行具有重要意义。

一些案例表明，当不合理设置最小相间距禿时，可能会导致电气设备的发生故障，甚至对人身和财产造成严重威胁。

通过对一些实际案例的分析，可以更深入地理解不同回路不同相导线间的最小相间距禿对电气系统安全的重要性，以及合理设置最小相间距禿对提高系统可靠性的作用。