3.4 组合图形的周长

三年级上册周长讲解一、周长的定义周长是指一个封闭图形边缘的长度。

简单来说，就是围绕一个平面图形的边的总长度。

二、直边图形周长的计算对于具有直边的图形，如正方形、长方形等，周长的计算相对简单。

以正方形为例，假设每一边的长度为a，则正方形的周长为4a。

对于长方形，周长等于两倍的（长+宽）。

三、曲边图形周长的计算对于曲边图形，如圆，计算周长需要用到特定的公式。

圆的周长，也称为圆的周长或圆的边界长度，是圆边缘的长度。

数学符号表示为C，公式为：C = 2πr，其中r为圆的半径。

四、周长的实际应用在实际生活中，周长的概念有许多应用。

例如，计算矩形区域的周长可以帮助确定所需的篱笆或围墙的长度；在图形设计或图案制作中，周长可以帮助确定所需的材料量。

五、组合图形的周长计算当两个或更多的图形组合在一起时，要计算整个组合图形的周长，需要分别计算各个图形的周长，然后将它们相加。

但是有些情况下，可能需要特殊的技巧或公式来计算组合图形的周长。

六、周长的变化规律1.增加边长：当一个多边形的每条边都按相同的长度增加时，其周长也会相应增加。

增加的长度等于每条边增加的长度乘以边的数量。

2.缩减边长：当一个多边形的每条边都按相同的长度缩减时，其周长也会相应减少。

减少的长度等于每条边减少的长度乘以边的数量。

3.增加或减少顶点：当一个多边形增加或减少一个顶点时，其周长会发生变化。

这种变化的规律可以通过分析图形的结构来确定。

在一般情况下，增加一个顶点会使周长增加两条边的总长度；而减少一个顶点会使周长减少两条边的总长度。

4.变形规律：当一个多边形发生变形时，其周长也会发生变化。

这种变化的规律取决于变形的类型和程度。

在一般情况下，变形程度越大，周长的变化越大。

变形可能是通过拉伸、压缩、旋转等方式进行的。

5.规律总结：通过以上分析可以得出结论：多边形的周长变化规律取决于边长的变化、顶点的增减以及变形的程度。

这些因素的综合作用决定了周长的变化情况。

教学内容概要学生：初中数学备课组教师：王老师年级：小五日期上课时间:学生上课情况：主课题：巧求周长与面积教学目标：1、复习巩固小学阶段平面几何的相关知识2、针对特殊的图形进行几何图形的周长和面积的拓展训练教学重点：1.组合图形的周长的巧妙求法2.组合图形面积的巧妙求法教学难点：1.组合图形的周长的巧妙求法2.组合图形面积的巧妙求法家庭作业1.讲义上相关练习考点及考试要求：1.直线型图形面积及周长教学内容【前课回顾】 上节课作业评讲。

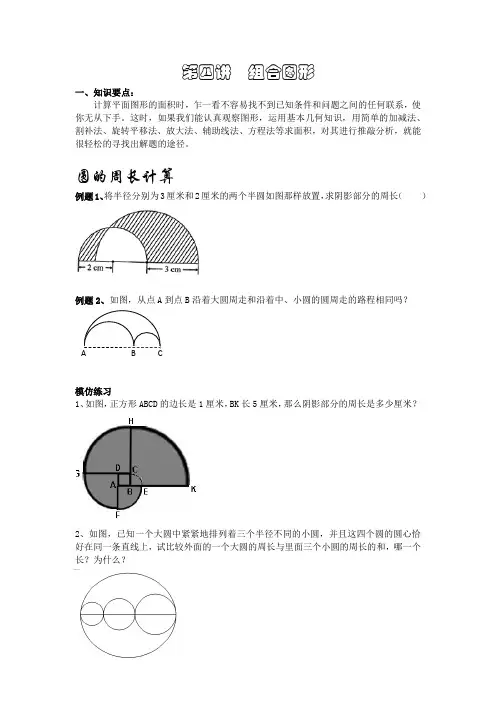
【知识精要】一、知识回顾：我们以前学过哪些几何图形？主要考察哪几个方面的知识？具体的计算公式有哪些？ 二、例题精讲：（巧求周长）【例1】 （2007年“希望杯”第一试）右图中的阴影部分BCGF 是正方形，线段FH 长18厘米，线段AC 长24厘米，则长方形ADHE 的周长是__________厘米。

【分析】 由于图中阴影部分BCGF 是个正方形，其四条边的边长都相等，且等于长方形ADHE 的宽。

FH AC +的和应为长方形ADHE 的长加上正方形BCGF 的边长，所以等于长方形ADHE 的长与宽之和。

所以长方形ADHE 的周长为：(1824)284+⨯=厘米。

【例2】 如右图所示，在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L 形区域乙和丙。

甲的边长为4厘米，乙的边长是甲的边长的1.5倍，丙的边长是乙的边长的1.5倍，那么丙的周长为多少厘米？EF 长多少厘米？【分析】 乙的周长实际上是正方形AHJE 的周长（我们可将乙与甲重合的两条线段分别向左、向下平移），同样的，丙的周长也就是正方形ABCD 的周长。

由于4 1.56AE =⨯=，6 1.59AD =⨯=，所以丙的周长为9436⨯=厘米，642EF AE AF =-=-=（厘米）。

【例3】 用若干个边长都是2厘米的平行四边形与三角形（如右图）拼接成一个大的平行四边形，已知大平行四边形的周长是244厘米，那么平行四边形和三角形各有多少个？【分析】 大平行四边形上、下两边的长为(24422)2120-⨯÷=厘米，观察上边，每6厘米有两个平行四边形的边，所以共有小平行四边形1206240÷⨯=个，三角形的数量与小平行四边形的数量相等，也是40个。

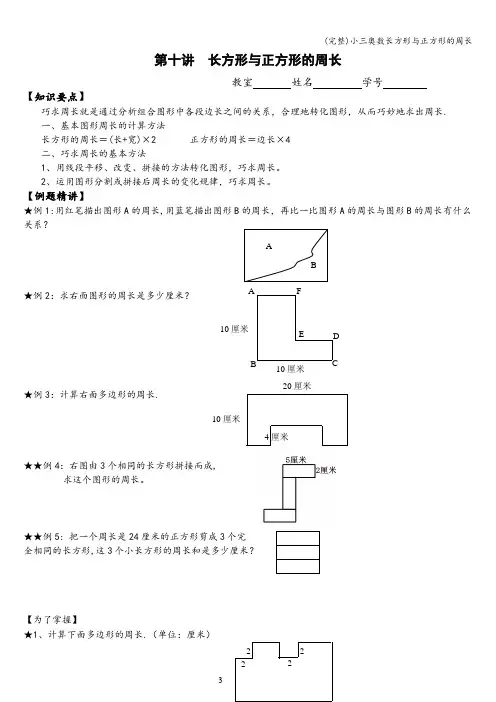
第十讲 长方形与正方形的周长教室 姓名 学号【知识要点】巧求周长就是通过分析组合图形中各段边长之间的关系，合理地转化图形，从而巧妙地求出周长. 一、基本图形周长的计算方法长方形的周长＝(长+宽)×2 正方形的周长＝边长×4 二、巧求周长的基本方法1、用线段平移、改变、拼接的方法转化图形，巧求周长。

2、运用图形分割或拼接后周长的变化规律，巧求周长。

【例题精讲】★例1:用红笔描出图形A 的周长,用蓝笔描出图形B 的周长，再比一比图形A 的周长与图形B 的周长有什么关系？★例2：求右面图形的周长是多少厘米？★例3：计算右面多边形的周长.★★例4：右图由3个相同的长方形拼接而成,求这个图形的周长。

★★例5: 把一个周长是24厘米的正方形剪成3个完 全相同的长方形,这3个小长方形的周长和是多少厘米？【为了掌握】★1、计算下面多边形的周长.（单位：厘米）ABAFBCED 10厘米10厘米 20厘米10厘米4厘米322 22★2、一个正方形的边长是2厘米，由6个这样的正方形拼成一个长方形,周长最长是几厘米？★3、右面多边形的周长是几厘米？（单位:厘米)★4、两个大小相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少了18厘米，则拼成的长方形的周长是多少？★5、计算下列图形（左图）的周长(单位:厘米)。

【为了优秀】★★1、如图，阴影部分是正方形,求出图中长方形ABCD 的周长.★★2、如图所示，用4个一样大的长方形和一个小正方形，拼成一个边长为56厘米的正方形,每个长方形的周长是多少厘米?★★3、正方形A 的周长是28，B 的周长是20，求由A 、B 组成的图形周长（如下图）。

43 12810厘米7厘米32★★4、一张长方形纸，长是31厘米，宽是16厘米。

先剪下一个最大的正方形，再从余下的纸片中剪下一个最大的正方形。

问最后余下的长方形的周长是多少？【为了竞赛】★★★1、一个正方形被分成了三个相同的长方形。

《组合图形的周长》教案
组合图形的周长教案
目标
本课程的目标是教授学生如何计算组合图形的周长。

知识点
- 了解周长的概念
- 掌握计算直线段和弧线的周长公式
- 研究如何计算组合图形的周长
教学步骤
1. 引入周长的概念并解释其意义
- 给学生展示不同形状的图形，并让他们讨论周长的定义
2. 计算直线段的周长
- 解释如何计算直线段的周长：周长等于直线段的长度3. 计算弧线的周长
- 解释如何计算弧线的周长：周长等于圆的周长乘以弧线的角度除以360
4. 组合图形的周长计算
- 给学生展示一些由直线段和弧线组成的图形，并让他们计算图形的周长
- 强调需要先计算每个直线段和弧线的周长，然后将它们相加
5. 练与应用
- 给学生一些练题，让他们计算组合图形的周长
- 鼓励学生应用所学知识解决实际问题
总结
本课程教授学生如何计算组合图形的周长。

通过研究直线段和弧线的周长计算公式，学生能够掌握如何计算组合图形的周长，并能应用这些知识解决实际问题。

三年级不规则图形周长怎么计算
三年级不规则图形周长的求法有：
1、将图形分为几个规则图形。

2、分别求出各个规则图形周长。

3、将各个周长加起来，结果就是不规则图形周长。

不规则图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。

环绕有限面积的区域边缘的长度积分，叫做周长，也就是图形一周的长度。

不规则的图形计算面积
1、分图法：用分割法或添补法，把不规则图形分成会计算的简单图形。

2、填补法：把不规则图形补成一个规则的图形，再以总面积减去填补上去的图形的面积。

3、找条件：分别计算简单图形的面积。

4、算面积：最后求和或差。

北师大版三年级数学上册第98页第5题《从“拼成图形的周长”说起》拓展练习教学设计一．教学内容：北师大版数学三年级 (上) 数学 98页第五题，拼成图形周长的拓展练习。

二．前测学情分析：应测52人，实测46人。

第1小题，错误9人，主要错在找第1和第3两个拼接图形的边线，占总人数的19.56%。

第3小题：有10人做错，占总人数的21.74%；有25人用的方法都是先找到新图形的长，再用周长公式去进行计算，占总人数的54.35%；有11人用的方法是将围成图形一周的长度进行累加，占总人数的23.91%；还有2名同学在教师的引导下，还想到了可以用原图形的周长和减去重合边的办法求新图形的周长，仅占总人数的4.35%。

从前测反馈的情况可以看出：1.学生对周长的概念本质理解不够，尤其是组合图形的周长；2.学生在解决拼成图形的周长问题时已经形成了统一的答题模式，思维固化，缺乏必要的拓展与发散。

三．设计思路：图1 从“拼成图形的周长”说起前测学习单从三个层次去拓展：1.认知的拓展：小学生三年级正处于由形象思维过渡到抽象思维的关键期，结合前测的数据分析，以学生已有经验为本节课的起点，通过问题串（周长是什么？在哪里？怎么算？），唤醒学生对周长本质的理解。

注重知识的生长点和延伸点，通过拼、画、找、算等符合认知规律的操作，带动多感官参与，逐步拓展学生的空间观念。

2.思路的拓展：从拼到画，从数到算，学生经历主动研究、分析、比较的思维过程，再通过生生对话、师生对话将思考的过程完整呈现，思维进阶的梯度在课堂中可见、可感。

观察拼接图形周长的视角多样，从学生只会运用基本方法计算图形一周的长度，到观察到边的增与减和周长的变化，不同角度去思考。

3.策略的拓展：学生在具体情境中发现。

当条件受到限制时，我们需要灵活运用不同的策略解决实际问题，发展学生的推理意识、应用意识。

四．教学目标：1.通过回忆周长的概念，在拼一拼、找一找的活动中，加深对周长概念的认识与理解；2.经历拼、剪活动，感受周长的变化，体会方法多样性，通过操作、想象、分析、判断等活动，发展学生的空间观念；3.在探究拼接图形的周长问题过程中，丰富解决相关图形与几何问题的策略，促进学生探索精神、创新意识的发展。

组合图形的练习题一、选择题1. 下列哪个选项不是组合图形的组成部分？A. 矩形B. 三角形C. 圆形D. 直线2. 组合图形的面积计算通常需要使用以下哪种方法？A. 直接测量B. 割补法C. 目测估计D. 公式计算3. 在组合图形的计算中，以下哪个概念是不需要考虑的？A. 对称性B. 相似性C. 比例性D. 颜色二、填空题4. 一个由两个等腰三角形组成的组合图形，如果两个三角形的底边长度相等，那么它们的面积之和等于________。

5. 如果一个组合图形由一个正方形和一个圆形组成，且正方形的边长等于圆形的直径，那么这个组合图形的面积是________。

三、计算题6. 一个组合图形由一个矩形和一个半圆形组成，矩形的长为10厘米，宽为5厘米，半圆形的半径为5厘米。

求这个组合图形的面积。

7. 一个由两个相等的直角三角形组成的组合图形，两个三角形的直角边长均为4厘米。

求这个组合图形的周长。

四、解答题8. 一个组合图形由一个等边三角形和一个正方形组成，等边三角形的边长为6厘米，正方形的边长为8厘米。

求这个组合图形的周长和面积。

9. 一个组合图形由一个圆形和一个矩形组成，圆形的直径为12厘米，矩形的长为15厘米，宽为10厘米。

求这个组合图形的面积。

五、应用题10. 一个公园的平面图由一个矩形和一个圆形组成，矩形的长为200米，宽为150米，圆形的直径为100米。

如果公园的管理者想要在公园的边缘种植一圈树木，每棵树之间的距离为5米，请计算需要种植多少棵树。

11. 一个设计师正在设计一个由两个相等的直角三角形组成的组合图形，用于制作一个装饰物。

如果直角三角形的直角边长为x厘米，设计师希望装饰物的周长为20厘米，求x的值。

六、证明题12. 证明：如果一个组合图形由两个相等的直角三角形和一个矩形组成，且直角三角形的直角边长等于矩形的宽，那么这个组合图形的面积等于矩形面积的两倍。

七、创新题13. 设计一个由至少三种不同图形组成的组合图形，并给出其面积的计算方法。

小学数学“长方形和正方形”单元“教学评一致性”教学设计《义务教育数学课程标准(2022年版)》的“课程内容”中强调“教—学—评”的一致性，明确了每一个单元的“内容要求”“学业要求”和“教学提示”。

“长方形和正方形”是人教版教材三年级上册第七单元的教学内容，该单元的“学业要求”是能说出长方形和正方形的特点，能说出图形之间的共性与区别；会测量三角形、长方形和正方形的周长，会计算长方形、正方形的周长；在解决图形周长的实际问题过程中，逐步积累操作的经验，形成量感和初步的几何直观。

下面将以人教版教材三年级上册“长方形和正方形”单元为例，在制订单元作业框架、设计单元核心作业和改进教学活动建议等基础上打造单元作业，使其更加贴近学生的认知水平。

一、制订单元作业框架单元作业框架能为教师指明单元主题、单元教学习目标、单元作业目标，以及获取学生学习结果表现，让教师更加清楚学生的学习路径。

人教版教材三年级上册“长方形和正方形”单元属于“图形与几何”领域，分为三个学习阶段：第一阶段主要教学四边形的初步认识和长方形、正方形的特征；第二阶段主要教学周长的含义及长方形、正方形的周长计算；第三阶段主要教学如何运用四边形及周长的知识解决生活中的实际问题。

1.确定单元作业目标通过教学目标引领作业目标，就能使作业目标与教学目标一一对应。

“长方形和正方形”单元教学目标和单元作业目标如表1所示。

2.确定学生学习结果表现根据单元作业目标精选练习题，才能有针对性地评价学生的学业水平。

“长方形和正方形”单元作业目标和对应的练习及学生学习结果表现如表2所示。

二、设计单元核心作业单元核心作业具有目标具体化、框架清晰化、过程开放化、思维可视化等特征，采用开放性的题目设计表现性任务，以了解学生的思维水平层次，了解学生在学习四边形及其周长的过程中存在哪些困难。

1.确定单元核心作业框架及水平层次人教版教材三年级上册“长方形和正方形”单元的核心目标是认识四边形以及长方形和正方形的特征，掌握长方形和正方形的周长公式，发展学生的空间观念、几何直观、推理意识、应用意识等核心素养。