组合图形的周长

三年级上册复合图形周长计算练习题复合图形是由多个基本图形组合而成的图形，计算其周长需要将各个基本图形的周长相加。

在三年级上册学习过程中，复合图形周长计算是一个重要的内容。

本文将给出一些复合图形周长计算的练习题，帮助同学们巩固理解和掌握这一知识点。

1. 小明画了一个由一个矩形和一个正方形组成的复合图形，其中矩形的长为6cm，宽为3cm，正方形的边长为4cm。

求这个复合图形的周长。

解析：首先计算矩形的周长，公式为周长=2*(长+宽)，代入数据得周长=2*(6+3)=18cm。

然后计算正方形的周长，公式为周长=4*边长，代入数据得周长=4*4=16cm。

最后将矩形和正方形的周长相加，得到复合图形的周长为18+16=34cm。

2. 阳阳画了一个由两个圆和一个矩形组成的复合图形，其中大圆的直径为10cm，小圆的半径为3cm，矩形的长为7cm，宽为4cm。

求这个复合图形的周长。

解析：首先计算大圆的周长，公式为周长=π*直径，代入数据得周长=π*10≈31.42cm。

然后计算小圆的周长，公式为周长=2*π*半径，代入数据得周长=2*π*3≈18.85cm。

接着计算矩形的周长，公式为周长=2*(长+宽)，代入数据得周长=2*(7+4)=22cm。

最后将三个图形的周长相加，得到复合图形的周长为31.42+18.85+22≈72.27cm。

3. 一块操场被两条平行的长方形跑道围绕，内跑道的长为60m，宽为5m，外跑道的长为80m，宽为5m。

求这个复合图形的周长。

解析：首先计算内跑道的周长，公式为周长=2*(长+宽)，代入数据得周长=2*(60+5)=130m。

然后计算外跑道的周长，公式同样为周长=2*(长+宽)，代入数据得周长=2*(80+5)=170m。

最后将两个跑道的周长相加，得到复合图形的周长为130+170=300m。

通过以上的练习题，同学们可以进一步熟悉和掌握复合图形周长的计算方法。

同时，也可以将这些计算方法应用到实际生活中，例如测量围墙的周长、跑道的周长等等。

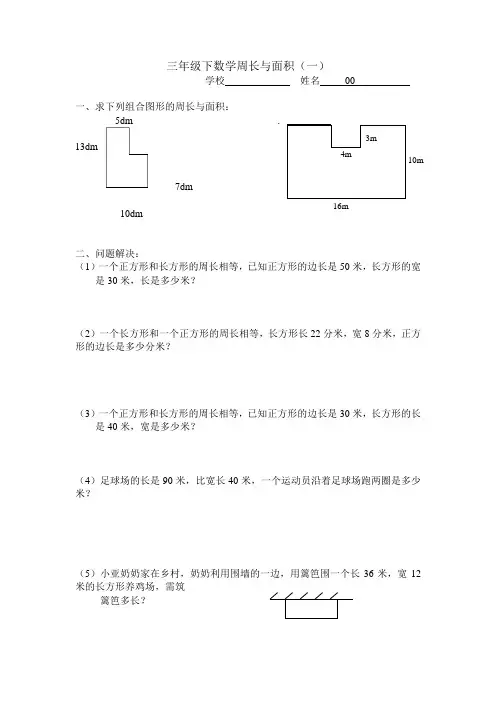
三年级下数学周长与面积（一） 学校 姓名 00一、求下列组合图形的周长与面积：5dm .13dm7dm10dm二、问题解决：（1）一个正方形和长方形的周长相等，已知正方形的边长是50米，长方形的宽是30米，长是多少米？（2）一个长方形和一个正方形的周长相等，长方形长22分米，宽8分米，正方形的边长是多少分米？（3）一个正方形和长方形的周长相等，已知正方形的边长是30米，长方形的长是40米，宽是多少米？（4）足球场的长是90米，比宽长40米，一个运动员沿着足球场跑两圈是多少米？（5）小亚奶奶家在乡村，奶奶利用围墙的一边，用篱笆围一个长36米，宽12米的长方形养鸡场，需筑篱笆多长？16m 4m 10m 3m（6）两个边长为3dm的正方形拼成一个长方形，这个长方形的周长是多少分米？（7）一个长方形的长是18厘米，宽是5厘米，如果长、宽各增加2厘米，面积增加多少？（8）把5个边长是3厘米的正方形，排成一个长方形，长方形的周长是多少？比正方形周长之和减少多少？（9）一个长方形的花坛长38dm，宽22dm，绕着这个花坛走两圈是多少m？如果一个人的步距约为3dm。

他绕花坛两圈共要走多少步？（10）会议室长10米，宽8米，用边长是4分米的地砖铺地，要用多少块？（11）这是小兔欢欢的家，中间是房间，周围是花园，房间是正方形，边长是8米。

A.25米B.在花园四周装上木栅栏，至少需要多少米长的木栅栏？（12）用24米长的篱笆围一个长方形的花坛，请你算一算，可以围成哪些面积？最大的面积是多少？三年级下数学周长与面积计算（二）1，计算下列图形的周长(单位：厘米)。

右上图是由边长为1厘米的11个正方形堆成的“土”字图形。

试求出其周长。

2，右图是某小学教学楼的平面示意图，设计者在图上只标明了三条线段的长度(单位：米)。

请你算出它的周长。

3，如右图所示，一个正方形被分成了三个相同的长方形。

如果其中一个长方形的周长是16米，那么这个正方形的周长是多少米？4，下面两图中的小方格的大小相同。

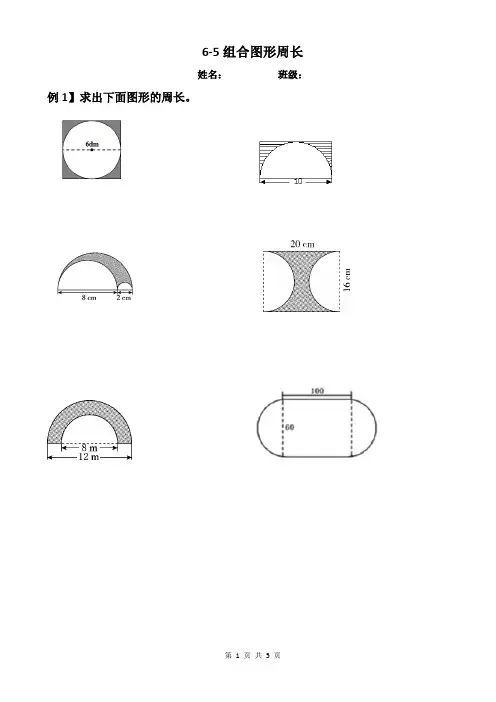
6-5组合图形周长姓名：班级：例1】求出下面图形的周长。

变式训练【例2】篮球场的三分线由两部分组成（如下图）。

一部分是半径为6.75米的半圆弧线，另一部分是与端线垂直的两条线段，每段长1.575米。

三分线大约长（________）米。

1、将半径分别为4厘米和3厘米的两个半圆如下图放置，则阴影部分的周长是（）。

A．21.98厘米B．27.98厘米C．25.98厘米D．31.98厘米2、下图阴影部分的周长是（________）厘米．（单位：厘米）【例3】如图，学校操场两端是半圆形，中间是正方形。

多多在操场上跑了3圈，一共跑了多少米？【变式训练】1.一块草地的形状如图的阴影部分，它的周长和面积各是多少？2.如图中圆的周长是25.12厘米，已知圆的面积和长方形面积相等，求阴影部分周长．3.如图，正方形边长为10cm，求阴影部分的周长．【例4】周叔叔用铁丝把3根直径是20厘米的圆木紧紧地捆在一起（横截面如图，不计接头），捆一周要用多少厘米铁丝？【变式训练】方法一：方法二：方法三：①如果接头处不计，方法二至少需要多长的绳子？②观察这三种捆扎方法，你有什么发现？【例5】如图所示赛场地，在400米比赛时，第三条跑道的起跑线画在第一条跑道起跑线的前面。

已知每条跑道宽1.5米，那么第三条跑道线应该画在第一条跑道线前面多少米？【变式训练】下图为赛车的比赛场地，交叉部分为立交桥形式，AB=CD=2000米，赛车左右两轮相距为2米．（1）赛车跑一圈后，哪侧车轮跑得多？多多少？为什么？（2）计算出左、右两侧车轮各跑多少米？(图中所示为左轮线路)【家庭作业】1.计算下列各图中阴影部分的周长．(1) (2)2.下面三幅图的阴影部分的周长相比较，（）．A．图(1)大B．图(2)大C．图(3)大D．同样大。

小学六年级数学求周长练习题一、概念回顾：在数学中，周长是一个非常重要的概念。

它是指一个图形的边界长度之和。

我们通常用单位长度（如厘米、米等）来表示周长。

在小学六年级，我们已经学习了很多关于周长的知识，接下来我们将通过一些练习题来复习和巩固这些知识。

二、单独图形的周长计算：1.矩形：(1) 矩形ABCD长为5厘米，宽为3厘米，求它的周长。

解析：根据矩形的性质，知道矩形的周长等于它的长加宽的两倍。

因此，矩形ABCD的周长=2 ×（5+3）= 16厘米。

2.正方形：(1) 边长为6厘米的正方形，求它的周长。

解析：正方形的周长等于它的边长乘以4，所以这个正方形的周长=6 × 4 = 24厘米。

3.三角形：(1) 边长分别为5厘米、7厘米和9厘米的三角形，求它的周长。

解析：三角形的周长等于它的三条边长之和，所以这个三角形的周长=5 + 7 + 9 = 21厘米。

4.圆形：(1) 半径为3厘米的圆形，求它的周长（取π≈3.14）。

解析：圆形的周长等于它的直径乘以π（或者半径乘以2π），所以这个圆形的周长≈3 × 2 × 3.14 ≈ 18.84厘米。

三、组合图形的周长计算：1.矩形和三角形的组合图形：(1) 如图所示，矩形ABCD的长为8厘米，宽为4厘米。

在矩形的上方，用三角形EBC和三角形AED连接起来，且三角形EBC的底边与矩形的下边平行。

求整个图形的周长。

解析：首先求矩形ABCD的周长=2 ×（8+4） = 24厘米；其次求三角形EBC的周长，根据三角形的性质，知道三角形的周长等于三边之和。

三角形EBC的周长 = 4 + 8 + 6 = 18厘米；最后根据矩形和三角形的位置关系，我们可以发现整个图形的周长等于矩形的周长减去三角形的底边长度，再加上三角形的周长。

所以整个图形的周长 = 24 - 4 + 18 = 38厘米。

2.圆形和正方形的组合图形：(1) 如图所示，半径为5厘米的圆形位于正方形EFGH的内部，且圆心O与正方形的四个顶点相切。

组合图形知识点总结一、组合图形的特点1. 组合图形是由多个基本图形组合而成的，可以是相同的基本图形也可以是不同的基本图形。

2. 组合图形的面积、周长等性质可以通过基本图形的性质进行计算得出。

3. 组合图形可以通过分解、合并等方法进行研究和计算。

二、组合图形的分类1. 立体图形的组合：由立体图形进行组合，比如立方体、长方体等。

2. 平面图形的组合：由平面图形进行组合，比如矩形、三角形、正方形等。

三、组合图形的性质1. 面积：组合图形的面积可以通过基本图形的性质进行计算得出，比如矩形、三角形、梯形等。

2. 周长：组合图形的周长可以通过基本图形的性质进行计算得出，比如矩形、三角形、正方形等。

3. 体积：组合图形的体积可以通过基本图形的性质进行计算得出，比如立方体、长方体等。

四、组合图形的计算方法1. 分解法：将组合图形分解成基本图形，然后分别计算每个基本图形的面积、周长等，最后进行合并得出组合图形的面积、周长等。

2. 合并法：将两个或多个基本图形合并成一个组合图形，然后计算组合图形的面积、周长等。

五、组合图形的应用1. 在建筑领域：设计和建造房屋、桥梁等都需要对组合图形进行计算和应用。

2. 在工业领域：制造各种产品时，也需要对组合图形进行计算和应用。

3. 在日常生活中：比如购买地砖、涂料等材料时，也需要对组合图形进行计算和应用。

六、常见组合图形的计算1. 矩形和圆形的组合：比如一个长方形花池中间有一个圆形喷泉，需要计算花池的面积和周长。

2. 正方体的组合：比如一个房子由多个长方体组合而成，需要计算整个房子的体积。

3. 矩形和三角形的组合：比如一个广场由一个大矩形和两个小三角形组成，需要计算广场的面积和周长。

总之，组合图形是一个非常重要的概念，它涉及到数学和生活中的许多方面，对于学生来说，掌握组合图形的知识是非常重要的。

希望通过本文的总结，能够对组合图形有更深入的理解，并能够在实际生活中灵活运用。

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

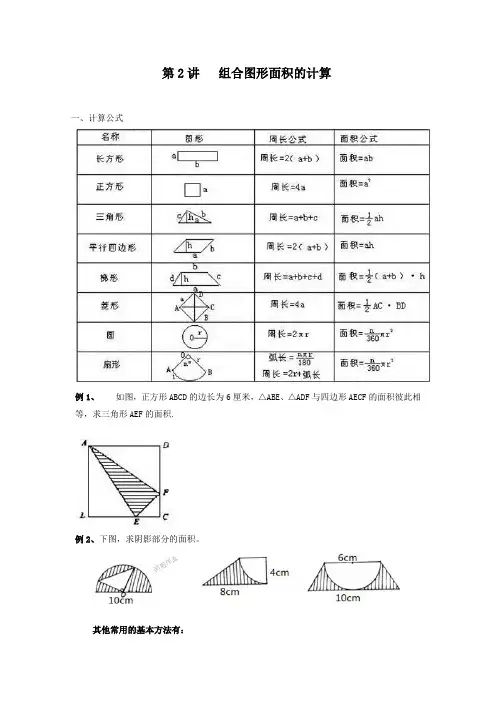
第2讲组合图形面积的计算一、计算公式例1、如图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.例2、下图，求阴影部分的面积。

其他常用的基本方法有：一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。

例如：求下图整个图形的面积二、相减法这方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

例如：下图，求阴影部分的面积。

一句话：正方形面积减去圆的面积即可。

三、直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积。

例如：下图，求阴影部分的面积。

一句话：通过分析发现阴影部分就是一个底是2、高是4的三角形。

四、重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可。

例如：下图，求阴影部分的面积。

一句话：拆开图形，使阴影部分分布在正方形的4个角处，如下图。

五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可例如：下图，若求阴影部分的面积。

六、割补法法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决。

例如：求阴影部分的面积．七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积。

例如：下图，求阴影部分的面积。

一句话：可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积。

例如图（1），求阴影部分的面积。

一句话：左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。

组合图形中圆的周长与面积一、学习目标：1．巩固加深对圆的周长与面积的理解与计算，掌握在组合图形中求圆的周长及面积的方法。

2．提高自己思维的灵活性。

二、知识基础：1．什么叫圆的周长？围成圆的曲线的长叫圆的周长。

什么叫圆的面积？圆所占平面的大小叫圆的面积？2．怎样求圆的周长和面积？圆的周长：c=πd 或c=2πr 。

圆的面积：2r S π=3．一个边长2分米的正方形剪下一个最大的圆，圆的周长为（6.28）分米。

面积为（3.14）平方分米。

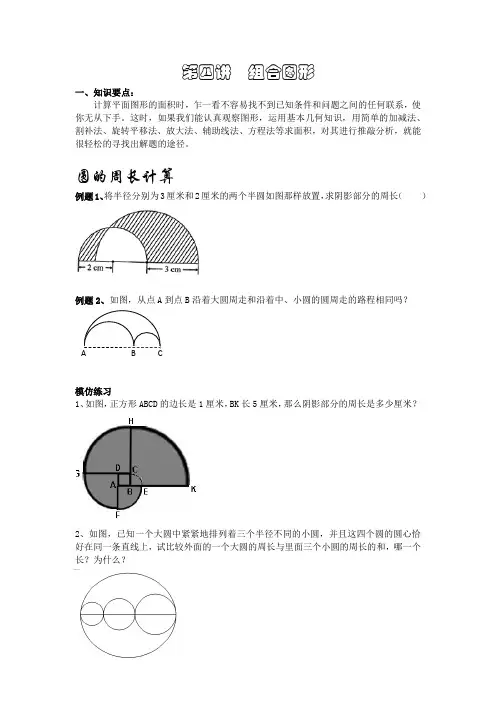
4．在一个正方形内做一个最大的圆，圆的面积是正方形面积的（4π） 正方形的边长就是圆的直径，设圆的直径为2r ，半径为r ，圆面积为2r π正方形边长就为2r ，正方形面积为24)2()2(r r r =⨯ 所以4422ππ==÷r r 正方形面积圆面积三、方法例谈例1：将半径分别为3厘米和2厘米的两个半圆如图放置，求阴影部分周长。

请认真看图：阴影部分周长是由哪些组合起来的？怎样分别求出这几部分的长度？厘米31=B O厘米1231212=-=-=O O A O A OAC=2—1=1厘米112r C O π=； 1121r C O π= 2221r C O π= cm r r C C O O 7.15214.3314.321212121=⨯+⨯=+=+ππ 阴影部分周长：厘米两个半圆7.197.15131=++=++AC B O答：阴影部分周长为19.7厘米例2：如图：从点A 到点B 沿大圆周长和沿着中、小圆的周长走，路程相同吗？①认真看图：大圆周是由哪几部分组成？中、小圆周是由哪几部分组成？②这题是要我们求什么？求大圆的半周长，求中、小圆的半周长，然后进行比较大小③怎样进行计算呢？设中圆直径为D ，小圆直径为d ，则：大圆直径为D+d ，所以d D d D C πππ2121)(21+=+=大 D C π21=中 d C π21=小 d D C C ππ2121+=+小中 所以：小中大C C C +=这就是说两种求法经过的路程是相同的。

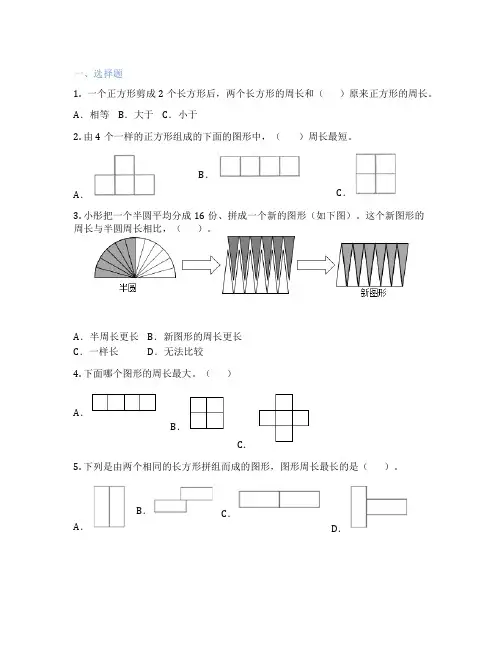
一、选择题1. 一个正方形剪成2个长方形后，两个长方形的周长和（）原来正方形的周长。

A．相等B．大于C．小于2. 由4个一样的正方形组成的下面的图形中，（）周长最短。

A．B．C．3. 小彤把一个半圆平均分成16份、拼成一个新的图形（如下图）。

这个新图形的周长与半圆周长相比，（）。

A．半周长更长B．新图形的周长更长C．一样长D．无法比较4. 下面哪个图形的周长最大。

（）A．B．C．5. 下列是由两个相同的长方形拼组而成的图形，图形周长最长的是（）。

A．B．C．D．二、填空题6. 算出下面图形的周长．(单位：厘米)________________7. 下面每个小正方形的边长都是1厘米，那么这个图形的周长是( )厘米。

8. 如图，是由六个正方形重叠而成的，连接点正好是各个正方形的中心．若正方形的边长为a，则该图形的周长是( )．9. 用3个长是10厘米，宽是5厘米的长方形拼成一个大长方形（如图），这个大长方形的周长是( )厘米；用这3个长方形还能拼成其它形状的大长方形，它的周长是( )厘米。

10. 小明将一张半圆形纸片平均分成四份后，重新组合在一起（如下图），新组合的图形的周长是( )cm（π取3）。

三、解答题11. 求下面各图中阴影部分的周长和面积．(单位:cm)（1）（2）12. 将一个长方形纸片从中间剪开，刚好剪成两个边长8厘米的正方形，原来这个长方形纸片的周长是多少厘米？13. 一个运动场如下图，两端是半圆形，中间是一个长方形，这个运动场的周长是多少米？14. 量出下图长方形每条边的长度，并算出他的的周长。

六年级数学上册组合图形的周长和面积21、如图12，已经半圆的直径为10㎝，求阴部分的面积及阴影弧线长的和。

22、如下图，已知AB=12厘米，且阴影部分甲的面积比阴影部分乙的面积大12平方厘米。

求BC的长是多少厘米？23、如下图，求出阴影部分的周长和面积。

（单位：㎝）24、如下图，已知AC=CD=DB=2㎝，求阴影部分的周长和面积。

25、已经半圆的直径为9㎝，求阴影部分的面积。

26、如下图，求阴影部分的周长与面积。

（单位：㎝）27、如图所示，圆的周长为12.56厘米，AC 两点把圆分成相等的两段弧，阴影部分（1）的面积与阴影部分（2）的面积相等，求平行四边形ABCD 的面积。

28、如图所示，直径BC ＝8厘米，AB ＝AC ，D 为AC 的重点，求阴影部分的面积。

DACB12ACDC29、 如图所示，AB ＝BC ＝8厘米，求阴影部分的面积。

30、 如图所示，求四边形ABCD 的面积。

（单位：厘米）31、如图19－16所示，BE 长5厘米，长方形AEFD 面积是38平方厘米。

求CD 的长度。

32.图19－17是两个完全一样的直角三角形重叠在一起，按照图中的已知条件求阴影部分的面积（单位：厘米）。

B45○7 C ABBC AE3819－1633、如图19－19所示，∠1＝15度，圆的周长位62.8厘米，平行四边形的面积为100平方厘米。

求阴影部分的面积（得数保留两位小数）。

34、如图19－20所示，三角形ABC 的面积是31.2平方厘米，圆的直径AC ＝6厘米，BD ：DC ＝3：1。

求阴影部分的面积。

35、如图19－21所示，求阴影部分的面积（单位：厘米。

得数保留两位小数）。

D304019－17 120519－1919－2030AB12 19－21三角形面积计算【例题1】已知如图，三角形ABC的面积为8平方厘米，AE＝ED，BD=2/3BC，求阴影部分的面积。

【思路导航】阴影部分为两个三角形，但三角形AEF的面积无法直接计算。

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。