组合图形中圆的周长与面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

专题01 圆的周长和面积（组合图形）答案解析一．计算题（共20小题）1．计算下面图形阴影部分的周长和面积。

（单位：厘米）【分析】根据题意，圆的直径为（4×3）厘米，阴影部分的周长等于圆的周长的一半加上5条4厘米长的线段之和，利用圆的周长公式：C＝πd，代入数据即可求出阴影部分的周长；阴影部分的面积等于圆的面积的一半减去边长为4厘米的正方形面积，分别利用圆的面积和正方形的面积公式求出这两个图形的面积，再相减即可得解。

××÷+×【解答】3.14(43)245×÷+＝3.1412220+＝18.8420＝38.84（厘米）2××÷÷−×3.14(432)244＝2×÷−3.146216×÷−＝3.1436216−＝56.5216＝40.52（平方厘米）即阴影部分的周长是38.84厘米，面积是40.52平方厘米。

2．如图中，大圆的半径等于小圆的直径。

请计算阴影部分的周长。

【分析】观察图形可知，阴影部分的周长＝大圆的周长＋小圆的周长，再根据圆的周长公式：C＝πd或C ＝2πr，据此进行计算即可。

【解答】3.14×2×4＋3.14×4＝6.28×4＋3.14×4＝25.12＋12.56＝37.68（cm）则阴影部分的周长为37.68cm。

3．计算下面图形的周长与面积。

【分析】周长等于大圆周长的一半加上两个半圆的周长（即一个小圆的周长）；面积等于大圆面积的一半减去两个小圆面积的一半（即一个小圆的面积），据此解答。

【解答】周长：3.14×40÷2＋3.14×（40÷2）＝125.6÷2＋3.14×20＝62.8＋62.8＝125.6（cm）面积：3.14×（40÷2） 2÷2－3.14×（40÷4） 2＝3.14×202÷2－3.14×10 2＝3.14×400÷2－3.14×100＝1256÷2－314＝628－314＝314（cm2）4．计算下边图形的周长和面积。

六年级圆的周长奥数题一、基础题型1. 一个圆的半径是3厘米，它的周长是多少厘米？- 解析：根据圆的周长公式C = 2π r（其中C表示周长，π通常取3.14，r为半径）。

当r = 3厘米时，C=2×3.14×3 = 18.84厘米。

2. 已知圆的直径是8分米，求这个圆的周长。

- 解析：因为圆的周长C=π d（d是直径），当d = 8分米时，C = 3.14×8=25.12分米。

3. 一个圆的半径扩大到原来的2倍，它的周长扩大到原来的几倍？- 解析：设原来圆的半径为r，则原来的周长C_1 = 2π r。

半径扩大2倍后变为2r，此时周长C_2=2π×(2r) = 4π r。

C_2div C_1=(4π r)div(2π r)=2，所以它的周长扩大到原来的2倍。

4. 有一个圆形花坛，半径是5米，在它的周围铺一条宽1米的小路，求小路的外沿周长是多少米？- 解析：小路的外沿半径为5 + 1=6米。

根据圆的周长公式C = 2π r，当r = 6米时，C=2×3.14×6 = 37.68米。

5. 一个半圆的直径是10厘米，求这个半圆的弧长（周长的一半）。

- 解析：圆的周长C=π d，半圆的弧长为(1)/(2)π d。

当d = 10厘米时，弧长=(1)/(2)×3.14×10 = 15.7厘米。

二、组合图形中的圆周长问题6. 正方形的边长为10厘米，在正方形内画一个最大的圆，求这个圆的周长。

- 解析：正方形内最大的圆的直径等于正方形的边长，即d = 10厘米。

根据圆的周长公式C=π d，C = 3.14×10 = 30.4厘米。

7. 长方形的长是12厘米，宽是8厘米，在长方形内画一个最大的半圆，求这个半圆的弧长。

- 解析：因为长方形的长是12厘米，宽是8厘米，所以这个半圆的直径最大为12厘米。

半圆的弧长=(1)/(2)π d=(1)/(2)×3.14×12 = 18.84厘米。

组合图形中圆的周长与面积一、学习目标：1．巩固加深对圆的周长与面积的理解与计算，掌握在组合图形中求圆的周长及面积的方法。

2．提高自己思维的灵活性。

二、知识基础：1．什么叫圆的周长？围成圆的曲线的长叫圆的周长。

什么叫圆的面积？圆所占平面的大小叫圆的面积？2．怎样求圆的周长和面积？圆的周长：c=πd 或c=2πr 。

圆的面积：2r S π=3．一个边长2分米的正方形剪下一个最大的圆，圆的周长为（6.28）分米。

面积为（3.14）平方分米。

4．在一个正方形内做一个最大的圆，圆的面积是正方形面积的（4π） 正方形的边长就是圆的直径，设圆的直径为2r ，半径为r ，圆面积为2r π正方形边长就为2r ，正方形面积为24)2()2(r r r =⨯ 所以4422ππ==÷r r 正方形面积圆面积三、方法例谈例1：将半径分别为3厘米和2厘米的两个半圆如图放置，求阴影部分周长。

请认真看图：阴影部分周长是由哪些组合起来的？怎样分别求出这几部分的长度？厘米31=B O厘米1231212=-=-=O O A O A OAC=2—1=1厘米112r C O π=； 1121r C O π= 2221r C O π= cm r r C C O O 7.15214.3314.321212121=⨯+⨯=+=+ππ 阴影部分周长：厘米两个半圆7.197.15131=++=++AC B O答：阴影部分周长为19.7厘米例2：如图：从点A 到点B 沿大圆周长和沿着中、小圆的周长走，路程相同吗？①认真看图：大圆周是由哪几部分组成？中、小圆周是由哪几部分组成？②这题是要我们求什么？求大圆的半周长，求中、小圆的半周长，然后进行比较大小③怎样进行计算呢？设中圆直径为D ，小圆直径为d ，则：大圆直径为D+d ，所以d D d D C πππ2121)(21+=+=大 D C π21=中 d C π21=小 d D C C ππ2121+=+小中 所以：小中大C C C +=这就是说两种求法经过的路程是相同的。

圆旳组合图形面积姓名：【知识与措施】要解决与圆有关旳题目，需要注意如下几点：1、纯熟掌握有关圆旳概念和面试公式：圆旳面积= 圆旳周长=扇形旳面积= 扇形旳弧长=（n是圆心角旳度数）2、掌握解题技巧和解题措施：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。

例1.求阴影部分旳面积。

(单位:厘米)解：这是最基本旳措施：圆面积减去等腰直角三角形旳面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分旳面积。

(单位:厘米)解：这也是一种最基本旳措施用正方形旳面积减去圆旳面积。

设圆旳半径为r，由于正方形旳面积为7平方厘米，因此=7，因此阴影部分旳面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分旳面积。

(单位:厘米)解：最基本旳措施之一。

用四个圆构成一种圆，用正方形旳面积减去圆旳面积，因此阴影部分旳面积：2×2-π＝0.86平方厘米。

例4.求阴影部分旳面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分旳面积。

(单位:厘米)解：这是一种用最常用旳措施解最常用旳题，为以便起见，我们把阴影部分旳每一种小部分称为“叶形”，是用两个圆减去一种正方形，π()×2-16=8π-16=9.12平方厘米此外：此题还可以当作是1题中阴影部分旳8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆旳3倍，问：空白部分甲比乙旳面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆与否相交、交旳状况如何无关）例7.求阴影部分旳面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5。

圆、组合图形的面积第一部分 知识梳理字母意义：O 圆心，r 半径，d 直径，π 圆周率,C 周长，S 面积 特征：同一圆内，所有的半径、直径都分别相等，直径等于半径的2倍 对称性：圆是轴对称图形，圆的直径所在的直线是圆的对称轴1.圆 圆的周长计算公式：C=πd=2πr ，半圆周长计算公式：C 半圆=πr+2r=(π+2)r 圆的面积计算公式推导过程：将圆沿着直径等分成若干个扇形（偶数份），再拼成一 个近似的长方形（分成的扇形越多，越接近长方形），长方形的长相当于圆的周 长一半（πr ），宽相当与圆的半径，圆的面积等于长方形的面积。

所以：S 圆=S 长方形=πr ×r=πr 2概念：两个半径不等的同心圆之间的部分称之为圆环。

各部分名称：①外圆：圆环中较大的圆叫做外圆，其半径通常用R 表示。

2.圆环 ②内圆：圆环中较小的圆叫做内圆，其半径通常用r 表示。

③环宽：外圆到内圆的距离叫做环宽 环宽=R —r圆环的面积计算方法：外圆的面积与内圆的面积之差是圆环的面积。

即：S 圆环=S 外圆—S 内圆 ,S 圆环=π(R 2 — r 2)弧：圆上任意两点间的部分叫做弧3.扇形 圆心角：弧的两个端点与圆心连结，所得两条半径的夹角叫圆心角 扇形：由圆心角的两条半径和圆心角所对的弧组成的图形叫扇形割补（平移）法 组合图形的面积 加减法计算策略1 旋转、对称法4.组合图形的 要求阴影先求空白 面积计算 包含与排除组合图形的面积 总面积=两部分面积和-重叠部分面积 计算策略2 巧添辅助线 等积转化（代换）第二部分精讲点拨例1判断下列各题是否正确：（1）圆的周长是直径的3.14倍。

（）（2）圆是轴对称图形，直径是圆的对称轴。

（）（3）世界上第一位把圆周率精确到七位小数的人物是祖冲之。

（）举一反三：1.填空题：（1）经过圆心并且两端都在圆上的线段叫做圆的（），圆有（）条直径。

（2）圆的面积推导公式是：将圆分成若干个扇形，再拼成一个近似的长方形，长方形的长相当于圆的（），长方形的宽相当于圆的（），所以圆的面积公式为（）。

圆的周长和面积公式1、（1）在同一个圆内或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的接近长方形。

长方形的长相当于圆的周长的一半，长方形的宽相当于圆的半径。

（2）拼出的图形与圆的周长和半径的关系。

圆的半径=长方形的宽圆的周长的一半=长方形的长2、圆面积的计算方法：因为长方形面积=长×宽，所以圆的面积=圆周长的一半×圆的半径。

即S圆=C÷2×r=πr×r=πr2圆的面积公式：S圆=πr2→r2=S圆÷π3、环形的面积：一个环形，外圆的半径用字母R表示，内圆的半径用字母r表示。

（R=r+环的宽度）S环=πR2-πr2或环形的面积公式：S环=π（R2-r2）（建议用这个公式）。

4、一个圆，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。

而面积扩大或缩小的倍数是这倍数的平方倍。

5、两个圆：半径比=直径比=周长比；而面积比等于这比的平方。

6、任意一个正方形与它内切圆的面积之比都是一个固定值，即4 :π。

7、当长方形，正方形，圆的周长相等时，圆面积最大，正方形居中，长方形面积最小。

反之，面积相同时，长方形的周长最长，正方形居中，圆的周长最短。

8、常用各π值结果：π= 3.14；2π= 6.28；5π=15.79、外方内圆（内切圆）公式S=0.86r2推导过程：S=S正-S圆=d2-πr2=2r×2r-πr2=4r2-πr2=r2×（4-π）=0.86r210、外圆内方（外切圆）公式S=1.14r2推导过程：S=S圆-S正=πr2-2r2=r2×（π-2）=1.14r2（把正方形看成两个面积相等的三角形，三角形的底就是直径，高是半径）11、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。

顶点在圆心的角叫做圆心角。

扇形的面积与圆心角大小和半径长短有关。

12、S扇=S圆×n/360°；S扇环=S环×n/360°13、扇形也是轴对称图形，有一条对称轴。

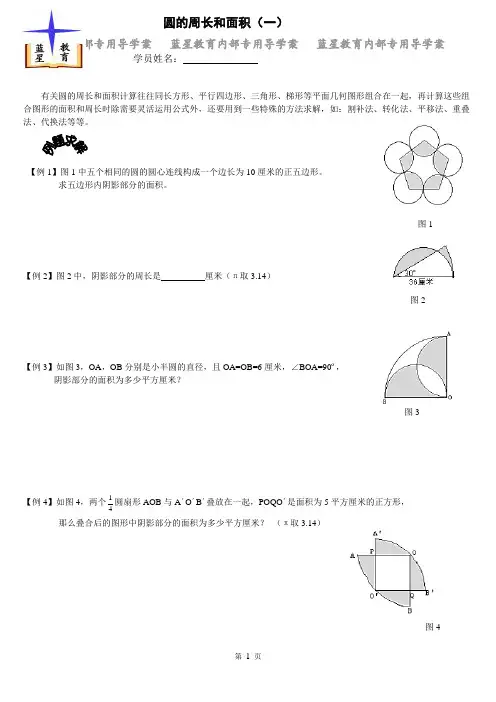
蓝星教育内部专用导学案 蓝星教育内部专用导学案 蓝星教育内部专用导学案学员姓名：有关圆的周长和面积计算往往同长方形、平行四边形、三角形、梯形等平面几何图形组合在一起，再计算这些组合图形的面积和周长时除需要灵活运用公式外，还要用到一些特殊的方法求解，如：割补法、转化法、平移法、重叠法、代换法等等。

【例1】图1中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形。

求五边形内阴影部分的面积。

【例2】图2中，阴影部分的周长是 厘米（π取3.14）【例3】如图3，OA ，OB 分别是小半圆的直径，且OA=OB=6厘米，∠BOA=90º， 阴影部分的面积为多少平方厘米？【例4】如图4，两个41圆扇形AOB 与A ´O ´B ´叠放在一起，POQO ´是面积为5平方厘米的正方形， 那么叠合后的图形中阴影部分的面积为多少平方厘米？ （π取3.14） 圆的周长和面积（一）图1图2图3图4【例5】如图5，一头羊被7米长的绳子拴在正五边形建筑物的一个顶点上，建筑物边长3米，周围都是草地，这头羊能吃到草地面积可达多少平方米？（π≈3）图5【例6】图6中的两块阴影部分的面积相等，三角形ABC是直角三角形，BC是直径，长40厘米，计算AB的长度。

图6【例7】如图7所示，等边三角形ABC的每边长2厘米，再将三角形ABC沿水平方向沿一条直线翻滚2003次，求A点所经过的总路程是多少厘米？（π取3计算）图7【例8】如图8所示，ABCD是平行四边形，AD=8㎝，AB=10㎝，∠DAB=30º，高CH=4㎝，弧BE，DF分别以AB，CD为半径，弧DM，BN分别以AD，CB为半径，阴影部分的面积为。

（精确到0.01）图8基础夯实图91、如图9所示，大圆半径为6，则其阴影部分的面积为。

2、已知正方形ABCD的边长为10㎝，过它的四个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，得到图10.那么图中阴影部分的面积为平方厘米（π取3.14）。

一、选择题1. 下图中正方形部分是一个水池，其余部分是草坪，已知正方形的面积是300平方米，草坪的面积是（）平方米。

A．B．C．D．不能确定2. 观察图形，对于两个图中阴影部分的叙述，（）是正确的。

A．周长、面积都不相等B．周长、面积都相等C．周长相等，面积不相等D．周长不相等，面积相等3. 如图，在长方形中有三个大小相等的圆，下列说法错误的是（）。

A．长方形的宽是4cmB．圆的半径是12cm的C．阴影部分的面积等于长方形的面积减去三个圆的面积4. 如图中阴影部分的面积是9平方厘米，图中圆环的面积是（）平方厘米。

A．18.84 B．56.52 C．81 D．28.265. 下面两个图中，关于涂色部分的描述正确的是（）。

A．周长和面积都不相等B．周长相等，但面积不相等C．周长不相等，但面积相等二、填空题6. 等腰直角三角形的一腰长是8厘米，以它的两腰为直径分别画两个半圆，那么，阴影部分的面积共有________平方厘米。

7. 如图：已知正方形的面积是10平方分米，那么阴影部分的面积是_____平方分米。

8. 如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内大正方形面积是小正方形面积的________倍。

9. 如图，一个正方形边长为10cm，一个直径为2cm的圆在正方形内部沿正方形四条边滚动一周，它所扫过的面积为( )cm2。

10. 下图有( )条对称轴，如果圆的直径是20dm，那么阴影部分的面积是( )。

三、解答题11. 如图，O是圆心，OD＝4，C是OB的中点，阴影部分面积是14π，求三角形OAB的面积。

12. 沈阳方圆大厦是一座古钱币造型的建筑。

小新模仿它设计了一个模型，模型的正面是铜钱的形状，其圆的直径是24cm，中间正方形的边长是0.8dm。

这个模型正面的面积是多少平方厘米？13. 求阴影部分的面积．（单位：厘米）14. 下图是一面我国唐代外圆内方的铜镜。