优质课数列的概念教学设计新部编版0001

数列的概念教学设计一、新概念的介绍数列是指由一组有序的数字组成的数字序列。

它们有一定的规律，可以根据特定规则依次求出下一个数字。

数列涉及到有关数学概念特别多，如序列、计数、归纳法、确定数列特征等，能提升学生学习数学的能力。

二、教学目标1.让学生了解数列的定义及概念；2.让学生掌握数列的特点和计算方法；3.使学生能够确定给定数列的公式：三、教学内容1．定义数列：将一组有一定规律的数字称之为数列。

2. 特性：数列具有一定的特性，如等差数列、等比数列等。

3.计算方法：学生可以使用归纳法确定数列的规则，并运用通项公式计算数列的值。

4. 题目分析：分析数列的给定条件，确定匹配的数列类型。

四、教学过程1. 通过图片和实际演示，向学生介绍数列：什么是数列；数列的定义；数列的特点；如何确定数列的特征；如何计算数列等；2. 让学生看影片或课本自学，例子：(1)让学生了解何为等差数列，利用加减乘除运算，理解求解数列的公式；(2)让学生了解何为等比数列，掌握等比数列的特点，确定等比数列的公式；(3)让学生分析实例，给定数列的条件，确定其所属的数列类型，求出数列所有元素；3.布置实践任务：让学生做数列相关的习题，分析数列，确定各类数列的特征，熟练掌握求解数列的步骤；4.学生达成的情况：达到教学目标后，学生可以自由探索，发现新的数列规律，做出数列习题。

五、教学反思经过本次数列的教学，学生已经掌握了数列的相关知识，能够依据公式进行数字列的运算，能够分析给定数列的特征，运用归纳法确定数列规律，有条件地发现新的规律。

下次教学应充分利用教学中拓展性，使教学更有趣；教学中要注意每个学生的认知，给予语言支持，使他们能更好地体会数列的规律性。

数列的概念教学设计（一）【三维目标】知识与技能 形成并掌握数列及其有关概念，及数列通项公式的意义；理解数列的表示方法与函数表示方法的关系。

过程与方法 培养学生观察、归纳、类比、联想等分析问题的能力，同时加深理解数学知识之间相互渗透性的思想。

情感、态度、价值观 激发学生学习数学的兴趣和积极性，陶冶学生的情操，培养学生坚忍不拔的意志，实事求是的科学态度和勇于创新的精神。

【教学重点】数列概念及其通项公式。

【教学难点】根据数列的前几项抽象、归纳出数列的通项公式。

【教学方法】诱思教学法，即教师通过问题诱导→启发讨论→探索结果，引导学生直观感知→观察分析→归纳类比→抽象概括，使学生在获得知识的同时，能够掌握方法、提升能力.【教学手段】多媒体课件辅助教学【学情分析】本节课的授课对象是省示范性高中的学生，学生基础扎实，思维灵活，适合进行新课程教学【教学过程设计】一、创设情景 引入课题1、章头故事： Titius 用一列数 3，6，12，24，48，96，192，… 推导从太阳到行星距离的经验定律，并探明一些行星。

2、观察下面几列数：① 4，5，6，7，8，9② ③ 3, 3.1, 3.14, 3.141, 3.1415, ……④ -1，1，-1，1，-1，1, ……⑤ 2，2，2，2，2， ……二、深化定义、巩固基础1.数列的定义:(1) 按一定次序排列的一列数叫做数列.(2) 数列中的每一个数都叫做数列的项,(3) 各项依次叫做这个数列的第1项11111,,,,, (2345)(首项),第2项,…,第n 项,…(n 为序号)（4）数列的一般形式可以写成有时简记为2. 通项公式的探索数列的每一项与这一项的序号对应关系序号 1 2 3 …… n↓ ↓ ↓ ↓项 1 13 15 (121)n - 可以看出项与项的序号之间可用一个公式：a n =121n -表示，该公式叫数列的通项公式。

如果数列的第n 项与n 之间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的通项公式 。

数列的概念教案数列的概念教案一、教学目标1. 了解数列的概念和定义；2. 能够判断一个数列的规律；3. 能够根据给定的数列规律，推导出数列的通项公式；4. 能够应用数列的概念解决实际问题。

二、教学内容1. 数列的概念和定义；2. 数列的通项公式；3. 数列的前n项和；4. 应用数列解决实际问题。

三、教学步骤步骤一：引入数列的概念通过举例子的方式，让学生观察一些数的排列，找出其中的规律性。

例如：1、2、3、4、5...；1、3、5、7、9...等。

并引导学生思考这些数的排列是否有一定的规律，如果有，我们可以将其称为数列。

步骤二：引出数列的定义根据学生的观察和理解，引出数列的概念和定义。

数列是由一列数按照一定的顺序排列而成的序列，其中每个数称为该数列的项，用an表示，n表示项的位置。

步骤三：数列的通项公式的引入引导学生在观察数列的过程中，思考如何得到数列中的每一项。

例如，对于数列1、2、3、4、5...，如果需要求第n个数，我们可以发现数列中的每一项都比前一项大1，所以第n个数可以表示为an = a1 + (n - 1)。

步骤四：数列的前n项和的引入引导学生思考如何求一个数列的前n项和。

例如，对于数列1、2、3、4、5...，如果需要求前n项的和S，我们可以发现数列中的每一项都比前一项大1，所以可以利用等差数列求和公式Sn = (a1 + an) / 2 * n，其中an = a1 + (n - 1)。

步骤五：应用数列解决实际问题通过实际问题的引入，让学生应用数列的概念解决问题。

例如，有一序列数：1、3、5、7、9...，要求求出第n项的值并求前n 项和。

引导学生观察数列规律，判断数列是等差数列，然后根据通项公式和求和公式计算出结果。

四、教学注意事项1. 引导学生在观察数列的过程中，思考数列的规律；2. 培养学生分析和推断的能力，让其能够根据已知规律求解未知项或和；3. 引导学生在解决实际问题时，将问题转化为数列问题，然后应用数列的概念解决问题。

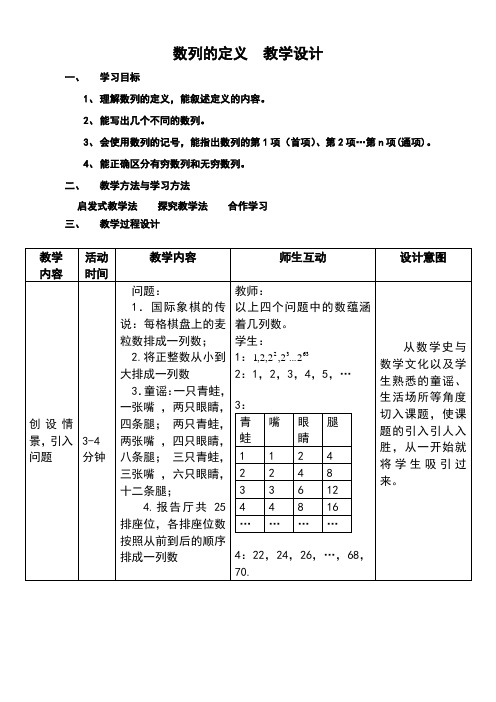
数列的定义教学设计一、学习目标1、理解数列的定义，能叙述定义的内容。

2、能写出几个不同的数列。

3、会使用数列的记号，能指出数列的第1项（首项）、第2项…第n项(通项)。

4、能正确区分有穷数列和无穷数列。

二、教学方法与学习方法启发式教学法探究教学法合作学习三、教学过程设计活动五：技能训练9-10分钟1、填空（1）2，4，6，8，（），12，…（2）1，3，5，（），9，11，…（3）-1，2，-3，4，（），…2、举出两个数列的例子3、判断下列数列哪些是有穷数列，哪些是无穷数列4、设数列{}n a为“1，，，指出其中，各是什么数，是数列的第几项用符号可以怎样表示学生独立完成训练，做完后相互讨论，相互评价，最后老师点评。

巩固本节课所学知识，独立完成练习，检验自己的掌握水平。

相互学习，提高整体学习效果。

课堂小结1分钟本节课学习了哪些知识这些知识的研究途径是什么1．数列的有关概念2．数列的分类3．数列的表示教师：小结概括了这节课的主要内容,使学生对这节课有个全面认识。

要有意识地引导学生去联想这一概念所涉及到的各个方面，沟通它们之间的联系，使学生能在新的高度上去重新认识和掌握基本概念，并灵活运用基本概念。

四、教学评价与反思1、通过概念课教学，力求使学生明确（1）概念的发生、发展过程以及产生背景；（2）概念中有哪些规定和限制的条件，它们与以前的什么知识有联系；（3）概念的名称、表述的语言有何特点；（4）概念有没有等价的叙述；（5）运用概念能解决哪些数学问题等。

目前，课时不足是数学新课程教学的突出问题，这会使概念教学受到严重冲击。

我认为在概念教学中多花一些时间是值得的，因为只有理解掌握了概念，才能更好地帮助学生落实“双基”，更好地帮助学生认识数学，认识数学的思想和本质，进一步地发展学生的思维，提高学生的解题能力。

2、让学生置身于知识的发生、发展过程中，经历直观感知、观察发现、抽象概括、符号表示等思维过程，展示“数学定义的严谨性”是对事物的感性认识的升华和提高，有助于提高学生分析问题和解决问题的能力。

《数列的概念与简单表示法》教学设计一、教学目标1、知识与技能目标理解数列的概念，能够区分数列、项、有穷数列、无穷数列。

掌握数列的通项公式，能根据通项公式写出数列的前几项。

了解数列的递推公式，能根据递推公式写出数列的前几项。

2、过程与方法目标通过实例引入，培养学生观察、分析和归纳的能力。

经历数列概念的形成过程，体会从特殊到一般的数学思维方法。

3、情感态度与价值观目标让学生感受数列在实际生活中的应用，激发学生学习数学的兴趣。

通过自主探究和合作交流，培养学生的创新意识和团队精神。

二、教学重难点1、教学重点数列的概念及通项公式。

利用通项公式求数列的特定项。

2、教学难点根据数列的前几项写出通项公式。

理解数列的递推公式。

三、教学方法讲授法、讨论法、练习法相结合四、教学过程1、导入新课通过展示一些生活中的数列实例，如银行存款利息的计算、树木的生长高度记录等，引导学生观察这些数据的排列规律，从而引出数列的概念。

2、讲授新课（1）数列的概念给出数列的定义：按照一定顺序排列的一列数称为数列。

强调数列中的数是有顺序的，并且同一个数在数列中可以重复出现。

让学生举例说明生活中的数列，如学生的身高排列、班级考试成绩排名等。

（2）数列的项介绍数列中的每一个数都叫做这个数列的项。

排在第一位的数称为这个数列的第 1 项（通常也叫做首项），排在第二位的数称为这个数列的第 2 项……排在第 n 位的数称为这个数列的第 n 项。

（3）有穷数列和无穷数列根据数列中项的个数，将数列分为有穷数列和无穷数列。

项数有限的数列叫做有穷数列，项数无限的数列叫做无穷数列。

通过实例让学生判断给出的数列是有穷数列还是无穷数列，如自然数列1，2，3，…，n，…是无穷数列，而1，2，3，4，5 是有穷数列。

（4）数列的通项公式设数列{an}的第 n 项与 n 之间的关系可以用一个公式来表示，那么这个公式叫做这个数列的通项公式。

以数列 2，4，6，8，…为例，引导学生尝试找出其通项公式为 an＝ 2n。

数列的概念教案教学目标：1. 理解数列的概念和基本特征；2. 能够识别数列中的常数项和通项；3. 能够根据规律确定数列的公式；4. 能够应用数列的特性解决问题。

教学准备：1. 幻灯片或白板、马克笔；2. 数列的示例题目。

教学过程：导入：（5分钟）1. 引入数列的概念：数列是指按照一定规律排列的一列数的集合。

数列中的每个数称为项。

2. 引导学生思考数列的例子：例如1，3，5，7，9是一个数列，其中的每个数都按加2的规律依次递增。

3. 提出问题：学生们有没有发现数列中的规律？如何确定数列的下一个数？探究：（15分钟）1. 给出示例数列：2，4，6，8，10，...2. 让学生观察数列，推测规律并列出下一个数。

3. 学生演示推理过程，例如：每个数都比前一个数大2，所以下一个数是12。

4. 引导学生总结：这个数列的规律是每个数比前一个数大2。

这个规律被称为数列的公式或通项公式。

5. 引入数列的常数项：数列中的某个特定项，如数列2，4，6，8，10，...中的10。

6. 引导学生区分常数项和通项。

示范与练习：（15分钟）1. 给出新的数列示例，如2，4，8，16，32，...2. 让学生观察数列，思考常数项和通项的确定。

3. 鼓励学生进行讨论，并给予提示，例如：每个数都是前一个数乘以2，所以通项公式为An = 2^n。

4. 让学生尝试应用通项公式计算数列的其他项。

拓展与应用：（10分钟）1. 给出更复杂的数列示例，让学生运用已学知识确定规律和通项公式。

2. 提供问题情境，让学生应用数列的概念解决实际问题。

归纳与总结：（5分钟）1. 学生回顾本节课学到的数列概念、特征和运用方法。

2. 教师总结并强调数列在数学和实际问题中的重要性。

展示与评价：1. 学生展示他们对数列概念的理解，可以通过口头回答问题或完成练习题的形式进行评价。

2. 教师给予反馈和评价，并鼓励学生进一步探究数列的性质和应用。

数列的概念教学设计教学目标：通过本课的学习，学生能够了解数列的概念，能够根据规律写出数列的通项公式，并能够应用数列的性质解决问题。

教学重点：1.掌握数列的概念及相关性质。

2.掌握数列的常见形式及其特点。

3.能够应用数列的性质解决实际问题。

教学难点：1.理解数列的概念并能够正确写出数列的通项公式。

2.能够应用数列的性质解决实际问题。

教学过程：一、导入（5分钟）1.教师提问：你们知道什么是数列吗？能给出一个例子吗？2.学生回答后，教师解释数列的概念，并给出一些数列的例子，引起学生的兴趣。

二、概念讲解（15分钟）1.教师通过幻灯片或板书，介绍数列的概念及其特点：数列是指按一定规律排列的一列数，其中每个数称为数列的项。

数列可以是无限个数或有限个数。

2.教师给出几个常见的数列形式（等差数列、等比数列等），并解释其特点和规律。

三、数列性质的引入（10分钟）1.教师通过示例和问题的形式引入数列的性质，例如：数列中相邻项之差（公差）相等的数列称为等差数列，数列中相邻项之比（公比）相等的数列称为等比数列等。

2.教师让学生观察和思考，探讨数列的性质对数列的规律和特点有何帮助。

四、数列通项公式的引入（15分钟）1.教师通过实例演示，让学生观察数列的规律，引导学生尝试写出数列的通项公式。

2.学生们合作讨论，试图找出数列的规律并写出通项公式。

3.教师给出解答并解释通项公式的含义和作用。

五、巩固与拓展（15分钟）1.教师出示一些数列问题，让学生应用数列的性质和通项公式解决问题。

2.学生们分组讨论、解答问题，并展示解题过程和答案。

六、小结与反思（5分钟）1.教师对本节课的内容进行小结，提出数列的重要性和应用领域。

2.学生进行反思，回答教师提问或写下自己的收获和思考。

教学资源和评估：1.教学资源：幻灯片、黑板、教材、练习题等。

2.教学评估：观察学生的参与情况、小组讨论的问题解答情况、个别讲解的合理性和准确性。

精选教课教课方案设计| Excellent teaching plan教师学科教课方案[ 20–20学年度第__学期]任教课科： _____________任教年级： _____________任教老师： _____________xx市实验学校《数列》教课方案一、设计思想本课课型为新讲课，睁开研究性教课。

采纳“3+2”教课方案模式：整体上分为三个板块（切入、发展、连结），每一板块又贯串两条主线（内容设计、互动设计）。

二、本课创新点1、采纳“ 3+2”教课方案方案，整体构造以下切入发展连结内容设计叙述中的思想互动（设问—意会—认可）超短互动（刺激—反响）思虑下的语言互动（实问—沉思—回答）互动设计练习（部署—点拨—讲评）限时练习（组织—指引）活动（内容—组织—评论）详细设计中将采纳以下记号T：（教师语言）T1：（教师大范围提示）T2：（教师小范围提示）T3：（教师更小范围提示）S：（学生语言假想）板书设计：用下划线表示活动设计：用小括号框定2、采纳片断多媒体教课，适合发挥计算机协助教课功能，易操作，提升备课效率。

三、教课对象剖析本课教课对象为高一学生，他们已经学习了会合、函数的基本知识，教师设计由原有知识的局部改变产生新的问题，考虑到学生能力上的差别，在教课方案中表现了对学生能力的不一样层次要求。

四、教材剖析数列是高中数学的重要内容之一，它有宽泛的应用，是学生此后进一步学习的基础知识，是培育学生数学能力的优秀题材。

本节先经过实例概括出数列的观点，而后介绍数列的通项公式，最后经过例题剖析介绍数学思虑的方法。

要点：数列的观点及通项公式；难点：依据数列的前几项写出数列的一个通项公式；要点：由各项的特色，找出各项共同的组成规律。

五、教法剖析研究性教课。

教师处于一种指引地位，让学生环绕教师或学生提出的问题睁开踊跃的思想，让学生处于一种自我表现状态。

教课中着重学生自己提出问题或自己提出解决问题的方法，教师率领学生找寻解决问题的门路，体验解决问题的过程，进而提升解决问题的能力，逐渐改变学生的学习方式 ,达成数列知识系统的建构过程。