【最新】九年级数学冀教版河北专用下册课件:河北常考点专题(九) 二次函数的图像与字母系数的关系(共10张
- 格式:ppt
- 大小:1.01 MB
- 文档页数:10
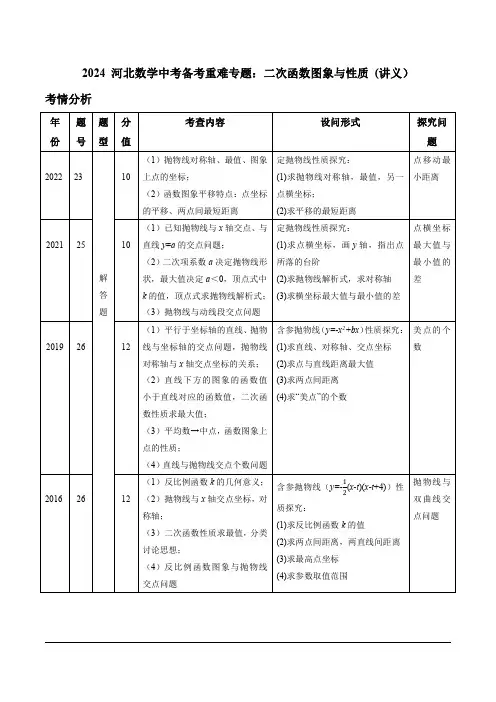
2024河北数学中考备考重难专题:二次函数图象与性质(讲义)考情分析年份题号题型分值考查内容设问形式探究问题202223解答题10(1)抛物线对称轴、最值、图象上点的坐标;(2)函数图象平移特点:点坐标的平移、两点间最短距离定抛物线性质探究:(1)求抛物线对称轴,最值,另一点横坐标;(2)求平移的最短距离点移动最小距离20212510(1)已知抛物线与x轴交点、与直线y=a的交点问题;(2)二次项系数a决定抛物线形状,最大值决定a<0,顶点式中k的值,顶点式求抛物线解析式;(3)抛物线与动线段交点问题定抛物线性质探究:(1)求点横坐标,画y轴,指出点所落的台阶(2)求抛物线解析式,求对称轴(3)求横坐标最大值与最小值的差点横坐标最大值与最小值的差20192612(1)平行于坐标轴的直线、抛物线与坐标轴的交点问题,抛物线对称轴与x轴交点坐标的关系;(2)直线下方的图象的函数值小于直线对应的函数值,二次函数性质求最大值;(3)平均数→中点,函数图象上点的性质;(4)直线与抛物线交点个数问题含参抛物线(y=-x2+bx)性质探究:(1)求直线、对称轴、交点坐标(2)求点与直线距离最大值(3)求两点间距离(4)求“美点”的个数美点的个数20162612(1)反比例函数k的几何意义;(2)抛物线与x轴交点坐标,对称轴;(3)二次函数性质求最值,分类讨论思想;(4)反比例函数图象与抛物线交点问题含参抛物线(y=-12(x-t)(x-t+4))性质探究:(1)求反比例函数k的值(2)求两点间距离,两直线间距离(3)求最高点坐标(4)求参数取值范围抛物线与双曲线交点问题20152511(1)求抛物线解析式、对称轴、顶点坐标;(2)抛物线与y轴交点坐标,二次函数性质求最值,二次函数增减性;(3)抛物线与线段交点问题(x轴),分类讨论思想含参抛物线(y=-(x-h)2+1)性质探究:(1)求抛物线解析式、对称轴、顶点坐标(2)求点纵坐标最大值,比较两点纵坐标大小(3)求参数h值抛物线与线段交点问题典例精讲例(2022河北定制卷改编)如图,抛物线y=x2+bx+c与直线y=x+2交于A、B两点,其中点A在y轴上,点B的横坐标是4,点P为抛物线上一动点,过点P作PC⊥x轴交AB于点C,设点P的横坐标为m.例题图(1)求抛物线的解析式;(2)若点P在直线AB下方的抛物线上,求出线段PC的最大值及此时点P的坐标;(3)若将原抛物线沿x轴平移,得到新抛物线y=(x+n)2+b(x+n)+c,要使新抛物线与线段AB 恰好有一个交点,求n的取值范围.(4)若原抛物线沿y轴平移,平移后的抛物线顶点恰好落在直线AB上,且交另一点为F,求平移的距离,点F的坐标.选题依据:此题考查学生对二次函数图象、对称轴、顶点坐标,平移,抛物线与直线交点问题,同时考查学生分类讨论和数形结合思想方法总结知识点:待定系数法求解析式、二次函数取值范围、图象开口、增减性、对称轴、顶点坐标、平移后的二次函数解析式解题方法:对称轴:①解析式已知,直接代入x=-2;②已知抛物线与x轴两交点,直接代入x=x+y2顶点坐标:①一般式:代入顶点坐标公式;②顶点式:直接得到顶点坐标;③交点式:化为顶点式求点与点、点与直线、直线与直线之间距离,先求得点坐标或直线解析式,通过横坐标或纵坐标间距离求得1.平移的特点:①二次函数图象的平移不改变开口大小(形状);②实质是图象上点的平移,可根据图象上任意一对对应点,即可确定平移方式,通常通过顶点来确定;2.抛物线中交点问题通常有:判断交点个数,通过交点个数求参数,抛物线与线段交点问题等,通常都是联立函数关系式,求二元一次方程组的解得以解决,在此类问题中通常会融合“整点”问题,选择满足“整点”的点即可;3.判断点是否在抛物线内问题:主要是利用极限思想,分类讨论思想,选择取值范围的两端点的x值分别代入求解即可.练习(2022河北预测卷)如图,抛物线y=-12x2+kx+4(k为常数)与x轴和y轴的正半轴分别交于点A和B.练习题图(1)当k=-1时.①直接写出抛物线的对称轴和顶点坐标;②当-2≤x≤1时,求抛物线的最大值与最小值的差;(2)直线L:y=6交y轴于点C,交抛物线于点M,N(M在N的左侧).当x≤12k时,抛物线的最高点到直线L的距离为2,请直接写出此时k的值.练习1(2022河北原创卷)如图所示为从游乐场的过山车抽象出来的函数图象,线段AB是一段平行于x轴的水平滑道,OA=3,滑道B-C-D可以看作一段抛物线,最低点为C(4,2),且D(6,3).滑道D-E-F是与滑道B-C-D的形状完全相同,开口方向相反的一段抛物线,其最高点为E,点F在x轴上,FO=12.练习题图(1)求抛物线B-C-D的解析式及线段AB的长;(2)求抛物线D-E-F的解析式,当小车(看成点)沿滑道从A运动到F的过程中,小车距离x 轴的垂直距离为2.5时,它到出发点A的水平距离是多少?(3)现在需要对滑道E-F部分进行加固,过E作支架EK⊥x轴于点K,然后建造如图所示的水平支架PS和竖直支架PM.求所有支架(虚线部分)长度之和L的最大值及此时点M的坐标.练习2(2022河北逆袭诊断卷)如图,在平面直角坐标系中,直线l1∶y=-12x+2与坐标轴交于A,B两点,与抛物线l2∶y=x2-2mx+m2-2交于C,D,过抛物线的顶点P向x轴作垂线,交直线l1于点Q.(1)当m=1时,求抛物线的解析式及点P的坐标;(2)若点Q的横、纵坐标都不小于0,当线段PQ取得最小值时,求△PCD的面积;(3)当抛物线与线段AB只有一个公共点时,直接写出m的取值范围.练习2题图答案典例精讲例解:(1)∵直线y=x+2经过点A,且点A在y轴上,∴点A横坐标为0,将x=0代入解析式y=x+2中,解得y=2,∴点A的坐标为(0,2),∵直线y=x+2经过点B,点B的横坐标是4,∴将x=4代入解析式y=x+2中,得y=6,∴点B的坐标为(4,6).∴将点A(0,2),点B(4,6)代入抛物线y=x2+bx+c中,得=2,16+4+=6,得=-3,=2,∴抛物线的解析式为y=x2-3x+2;(2)由(1)得抛物线的解析式为y=x2-3x+2,∴点P坐标为(m,m2-3m+2),∵PC⊥x轴交AB于点C,∴点C的坐标为(m,m+2),∴PC=m+2-(m2-3m+2)=-m2+4m=-(m-2)2+4,∵-1<0,0<m<4,∴当m=2时,PC有最大值,最大值为4,此时点P坐标为(2,0);(3)由(1)得,抛物线解析式为y=x2-3x+2=(x-32)2-14,∵将抛物线沿x轴平移n个单位长度,得到抛物线y=(x+n)2+b(x+n)+c,∴可设抛物线解析式为y=(x+n)2-3(x+n)+2=(x-32+n)2-14,通过图象可知,①当抛物线经过点A时,与线段AB恰有一个交点,将点A(0,2)代入抛物线解析式,得(-32+n)2-14=2,解得n1=3,n2=0(舍去),∴n的取值范围为0<n≤3;②当抛物线恰好经过点B时,与线段AB恰有一个交点,将B (4,6)代入抛物线解析式,得(52+n )2-14=6,解得n 1=-5,n 2=0(舍去),∴n 的取值范围为-5≤n <0.∴n 的取值范围为-5≤n <0或0<n ≤3.(4)由(1)得,抛物线解析式为y =x 2-3x +2=(x -32)2-14∵顶点坐标为(32,-14),32代入直线解析式y =32+2=72,顶点坐标为(32,72),∴平移距离=14+72=154,∴平移后抛物线y =(x -32)2+72,联立=(-32)2+72=+2,解得x =52x =32当=32时,交点为平移后抛物线顶点坐标(32,72)当=52时,交点F 坐标为(32,92).课堂练兵解:(1)①对称轴为直线x =-1,顶点坐标为(-1,92);【解法提示】∵k =-1,∴y =-12x 2-x +4=-12(x +1)2+92x =-1,顶点坐标为(-1,92).②由①得,抛物线y =-12x 2-x +4的对称轴为直线x =-1,12<0,∴当-2≤x ≤-1时,y 随x 的增大而增大,当-1<x ≤1时,y 随x 的增大而减小,∴当x =-1时,抛物线有最大值为92,∵-1-(-2)=1,1-(-1)=2,∴当x =1时,抛物线有最小值,最小值为52,∴当-2≤x ≤1时,抛物线的最大值为92,最小值为52,9-5=2;(2)k的值为-22或436.【解法提示】设直线x=12k交抛物线于点P,抛物线的顶点为R,∵y=-12x2+kx+4=-12(x-k)2+12k2+4,∴抛物线的对称轴为直线x=k,顶点R的坐标为(k,12k2+4),当x=12k时,y=-12×(12k)2+k×12k+4=38k2+4,∴P(12k,38k2+4).当k<0时,如解图①,当x≤12k时,最高点为R(k,12k2+4),∵抛物线的最高点到直线L的距离为2,12k2+4-6=2,解得k=-22或k=22(舍去);当k≥0时,如解图②,当x≤12k时,抛物线的最高点为P(12k,38k2+4),∵抛物线的最高点到直线L的距离为2,38k2+4-6=2,解得k=436或k=-436(不符合题意,舍去).综上所述,k的值为-22或436.解图②解图①课堂小练练习1解:(1)∵抛物线B-C-D的顶点为C(4,2),∴设抛物线B-C-D的解析式为y=a(x-4)2+2(a≠0),代入点D(6,3)得3=a(6-4)2+2,解得a=14,∴抛物线B-C-D的解析式为y=14(x-4)2+2.∵AB∥x轴,且OA=3,∴点B的纵坐标为3,令1(x-4)2+2=3,解得x1=2,x2=6,∵点D(6,3),∴点B的坐标为(2,3),∵点A在y轴上,∴AB=2;(2)∵抛物线D-E-F与抛物线B-C-D的形状完全相同,由(1)得抛物线B-C-D的解析式为y=14(x-4)2+2,∴设抛物线D-E-F的解析式为y=-14(x-h)2+k,∵FO=12,∴F(12,0),-14(6-ℎ)2+=3ℎ=8=4.将点D(6,3),F(12,0)代入,可得-14(12-ℎ)2+=0,解得∴抛物线D-E-F的解析式为y=-14(x-8)2+4.当小车距离x轴的垂直距离是2.5时,则2.5=14(x-4)2+2,解得x=4±2,或2.5=-14(x-8)2+4,解得x1=8+6,x2=8-6(不合题意,舍去),∴小车到出发点A的水平距离为4+2或4-2或8+6;(3)由抛物线y=-14(x-8)2+4,可得E(8,4),∴EK=4,K(8,0),设M(d,0)(8<d<12),∴点P(d,-14(d-8)2+4),则S P=d-8,PM=-14(d-8)2+4,∴所有支架的长度和L=d-8+[-14(d-8)2+4]+4,化简得L=-14(d-10)2+9,∵8<d<1214<0,∴当d=10时,L有最大值,最大值为9.此时点M的坐标为(10,0)练习2解:(1)∵m=1,y=x2-2mx+m2-2,∴将m=1代入y=x2-2mx+m2-2,得到抛物线的解析式为y=x2-2x-1=(x-1)2-2,∵点P为抛物线的顶点,∴点P的坐标为(1,-2);(2)∵抛物线y=x2-2mx+m2-2=(x-m)2-2,∴顶点P在直线y=-2上,∵点Q 的横、纵坐标都不小于0,∴点Q 在线段AB 上,如解图,当点Q 与点B 重合时,线段PQ 的值最小,过点C ,D 分别作PQ 所在直线的垂线,垂足分别为E ,F ,∵点B 的坐标为(4,0),∴x =--2m 2=m =4,∴抛物线的解析式为y =x 2-8x +14,=x 2-8x +14=-12x +2,可得x 2-8x +14=-12x +2,解得x 1=15+334,x 2=15-334,∴CE +DF =x 1-x 2=332,∴S △PCD =S △PBC +S △PBD=12PB ·CE +12PB ·DF =12PB ·(CE +DF )=12×2×332=332;解图(3)m 的取值范围为-2≤m <2或4-2<m ≤4+2.【解法提示】分两种情况讨论:①当抛物线过点A时,可得m2-2=2,解得m=2或m=-2,当m=2时,抛物线的解析式为y=x2-4x+2,=x2-4x+2=-12x+2,可得x2-4x+2=-12x+2,解得x1=0或x2=72,∵x2=72<4,∴两交点都在线段AB上,∴-2≤m<2;②当抛物线过点B时,可得(4-m)2-2=0,解得m=4+2或m=4-2,∴4-2<m≤4+ 2.。